动态规划——从斐波那契数列说起

各位老可爱们，又到了不按时更新的算法环节。本次文章是为了这个月的直播做铺垫，给大家说一说动态规划。动态规划是一种 "林品如" 方法，常常可以达到平地惊雷使人拍案叫手疼的效果。具体地说，你要是信手拈来一种动态规划方法，写在935数据结构算法题答题区域，那么我简直可以说，考场上的你一定按耐不住心中得意的小火苗，写完甚至生怕老师觉察不到这种方法是动态规划而一定要自己在解法上注明：此乃动态规划求解，给不给满分你看着办，希望老师你不要不识抬举。

所以说，动态规划不仅很符合考察者们的胃口，在某方面也可以表征出应答者的算法功底以及思维方式。简单地说，动态规划是一种以空间换时间的高效算法，它将中间结果储存下来，以便下一次计算到某个式子而这个式子依赖于以前的结果时，我们可以直接在存储中间结果（一般可能是数组存储）的地方拿出以前的结果来合成当前我们想要的式子的解，而不用重新计算之前的结果。

与动态规划相对的，递归便是一种非常简单易懂但是十分耗时的方法。相信大噶本科阶段老师一定举过斐波那契数列的例子：

已知斐波那契数列：1，1，2，3，... 其中第一个1是数列第1项，
第二个1是数列第2项，以此类推，请写出算法返回该数列的第n项。

当时老师一定说：跟你们港吼，介题奏系用递归做嘛，一丢丢难度也没有嘛。

没错，最简单易懂的方式就是用递归来求解。但是，聪明的你们，还记得一般递归的写法么？我知道大家一定都记得流程（其实我强烈怀疑这一点！！！！），所以我还是惹人烦地再写一遍吧：

1. 确定函数的功能。比如上面的求解斐波那契数列第n项，我们就希望有一个函数Fib(n)，可以接受一个参数n，然后返回第n项的斐波那契数。

2. 确定递归的初始条件。递归嘛，总不能一直递归吧，所以我们就需要看看啥时候可以结束递归。一般来说，结束的条件都是很简单的开始情况，比如这个题目中，啥时候你可以拍着胸脯说，这种情况一眼都可以看出来？n=1的时候可以么？可以呀，n=1的时候直接返回1不就可以了吗。是呀，你要是这么想我得说你很棒观察力敏锐。那n=2呢，你会说当然也行啦，n=2也返回1嘛。没错没错，我简直要给你喝彩了。是的呀，n=2的时候好像也挺简单的。咱们也把它当成基本情况吧。那你们肯定接着说，n=3的时候咱们也把它当成基本情况直接返回2行不行？当然也可以啦，一般来说，基本情况越多的话，递归可以越快地结束。但是我要说明的是，一般基本情况不能太少，太少了可能反而会出错。那有些小可爱就说啦：我啷个晓得基本情况得是几个嘞？啊，这个你们不用担心，你可以先写几个简单的情况，然后后期调试，如果你写的这几个简单的情况足以应付所有的测试例子，那么当然可以就这样不改了。如果你发现这么几个例子最后有些测试例子不通过，那说明你的基本情况可能少了，那你就加几个吧。这里我们就把n=1和2作为基本情况吧。

3. 前后状态之间的联系怎么写出来。因为递归就是不断缩小问题规模，假设你已经知道了Fib(n-1)的话，那怎么根据这个结果得到Fib(n)呢，这种联系就是我们第三步中要写出来的。针对这个题其实我们可以发现Fib(n)与Fib(n-1)以及Fib(n-2)有关系，具体地就是：

Fib(n) = Fib(n-1) + Fib(n-2)

所以前后关系的联系用这个式子就可以写出来了。很容易，根据上面三步写出下递归代码：

//1.确定函数的功能
int Fib(n){
    //2.确定递归的初始条件
    if(n == 1 || n == 2){
        return 1;
    }
    //3.前后状态之间的联系怎么写出来
    int res = Fib(n-1) + Fib(n-2);
    return res;
}

当然如果你要是加一个初始条件，写成下面这样也是可以的：

//1.确定函数的功能
int Fib(n){
    //2.确定递归的初始条件
    if(n == 1 || n == 2){
        return 1;
    }else if(n == 3){
        return 2;
    }
    //3.前后状态之间的联系怎么写出来
    int res = Fib(n-1) + Fib(n-2);
    return res;
}

但是，但是，你们都知道，递归一般非常耗费时间，这是为什么呢？因为递归存在大量的重复计算，它没用利用好之前的结果。比如说吧，计算Fib(4)的话，就先计算Fib(3)和Fib(2)： Fib(3)的计算得计算Fib(2)和Fib(1)，这个Fib(1)是基本情况直接有了，但是Fib(2)不是基本情况，得另外计算。

Fib(2)的计算得计算Fib(1) 和 Fib(1)，这俩都是基本情况，所以可以得到Fib(2)。

所以你们可以发现，计算Fib(4）的过程中，Fib(2)在Fib(3) 中计算了一次，在Fib(2)中又计算了一次。这两次计算都是重新计算，所以存在大量的这种重复计算，再加上递归函数本身不断的进栈出栈，所以递归一般来说就比较耗费时间。

 

所以，有没有什么办法可以规避这种重复计算呢？当然有，我们把之前计算的结果先存起来，等下次要用的时候，直接拿出来不就好了么，这就是鼎鼎有名的 '空间换时间' 的思想，也是动态规划最为本质的特点。

理论上来说，动态规划与贪心算法有着很强的联系，比如它们都具备最优子结构这一性质。不过，就算在这里说了，恐怕各位对其也还是不感兴趣。所以，本文中我就只谈怎么用动态规划求解，而不谈如何分析题目是否具备最优子结构来确定是否可以用动态规划求解。那么那么，小可爱又问了（话说你怎么这么多问题？？？^-^）：那我拿到了一个题目，怎么才能确定这个题是不是可以用动态规划求解呢？问得好！一般来说，有些比较经典的题目是需要大家心里有数的，这些题不仅是大家熟悉动态规划思维的必备题目，也是大家的小经验库。通常地，那种要求最什么什么情况下的题目，然后不要求给出具体的方案的题目都有可能使用动态规划求解。

好了说了这些多，让我们看看怎么用动态规划吧。动态规划的求解也有几个步骤：

1. 确定状态数组的含义。

2. 给状态数组的开始某几位赋初值。

3. 求出状态转移方程。

比如说，上面那个斐波那契数列题目要是用动态规划来做的话。我们就要考虑用一个容器将之前的计算结果存下来，方便以后需要的时候可以直接在这个容器中找而不是重新计算。一般地，这个容器我们用数组来表示（可能是一维数组，也可能是二维数组。而且因为动态规划的英文名称为dynamic program，所以这个状态数组一般在程序中就起名为dp），而且为了方便以后取用的时候我们知道拿容器中的哪一个，所以我们需要额外花心思来完成第一步，即确定状态数组的含义。比如这个题，我设定一个数组int[] dp = new int[n+1]。这个dp数组写法是java中的，长度为n+1，dp[i]表示第i项斐波那契数。至此，第一步我们就完成了。

现在我们考虑一下第二步，int[] dp = new int[n+1]这个语句写好之后，虽然确实定义了一个长度为n+1的数组dp，但是java会自动给dp中每一项都赋值为0。这个值自然不符合题目要求，所以我们的目的就是重新给dp赋值以满足dp[i]表示第i项斐波那契数这一个要求。第二步要求我们给开始某几位赋初值，这里我们令dp[1] = 1，dp[2] = 1 (dp[0] 我们就不管了，因为斐波那契没有第0项，这也是我们一开始设置dp长度为n+1而不是n的原因)，这一步我们也完成了。注意，这里和递归第二步一样，咱么也不确定初始要赋值几个，先赋两个再说，不够咱们后面再加几个。这样第二步咱们也完成了。

最后一步是最关键的一步，就是求出状态转移方程。其实斐波那契数列的通项表达式已经给了我们状态转移方程。也就是dp[i] = dp[i-1] + dp[i-2]。这一个题目比较简单，状态转移方程直接就出来了，但是有些题目需要自己考虑，这也是最难的一步。

通过上面的分析，我们就可以把动态规划求解斐波那契数列的代码写出来：

int Fib(n){
    if(n == 1 || n == 2)return 1;
    int[] dp = new int[n+1];
    dp[1] = 1;
    dp[2] = 1;
    for(int i=3;i<dp.length;i++){
        dp[i] = dp[i-1] + dp[i-2];
    }
    return dp[n];
}

很容易发现，上面的代码中，比如你要是计算dp[4]的话，你需要用dp[3] 和 dp[2]，但是由于循环从头往后遍历，所以当你求dp[4]的时候，dp[3] 和 dp[2] 已经求出来了，所以可以直接将dp[2] + dp[3] 加起来得到dp[4]，不涉及到递归中的重复计算。

---

好啦，是不是觉得这个题目太简单了，所以迫不及待想来一个正经题目练练手了？哦，圣母玛利亚，满足这个可爱孩子的愿望吧！blingbling，请看下面的题目：

已知一个int类型的数组nums,请求除nums的最长递增子序列的长度。
例如：nums=[4,-1,2,3,-5,7,10]这个数组的最长递增子序列的就是-1,2,3,7,10。长度为5，所以就返回5即可。
注意子序列和字串不一样，子串要求紧挨着，子序列可以不挨着，但是子序列必须保持相对顺序不变，
比如-1，2，3，4，7，10就不是一个子序列，因为4插队了。

好嘞，咱们康康怎么用动态规划来求吧。（聪明的你要不先想一个暴力的写法练练手再往下看？）

首先，这个题目是让咱们求最长递增子序列，符合最什么什么的要求，而且没让咱们把子序列写出来也符合只求结果不给方案的题目要求，所以我们初步判断可以用动态规划来做。

第一步，先确定一个dp数组，并给出其中元素的含义。这里咱们就设置一个和nums数组相等长度的dp数组吧，dp[i]的意义就是：以nums[i]为结尾的最长递增子序列的长度。所以最后dp中的最大值就是nums的最长递增子序列的长度（因为nums中最长递增子序列可能以nums数组中任何一个元素为结尾。）

第二步，咱们看看是不是要设定几个初值呀，我们发现，在没经过后续计算之前，以nums[i]元素为结尾的最长递增子序列的长度最少是1，就是nums[i]自己。所以这个题目我们需要先给dp中每个元素赋一个初值1。

第三步，啊，我们来看看最难的状态转移方程，或者说，后面的dp[i]的值怎么用前面的值来更新吧。想想看，比如下面这种情况： 

 

 

 

 

 

 

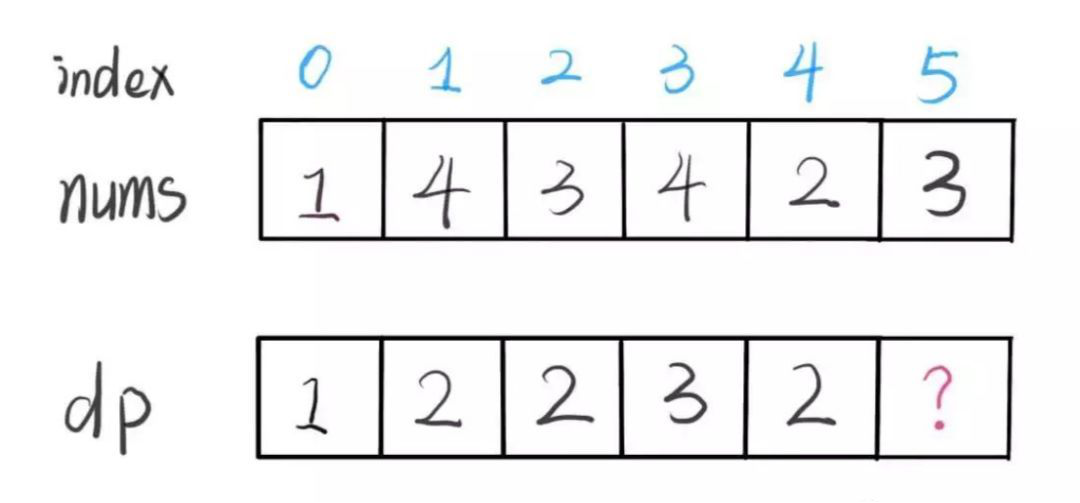
此时你打算计算dp[5]的值，而且nums[5] = 3。那么在前面1 4 3 4 2 这些数中，只要有一个数比nums[5] = 3要小，我们自然可以把nums[5] = 3这个数放到它后面组成一个递增子序列，考虑到这一步，dp[5]就好求了。首先我们看看nums[0] = 1这个数，是的比3小，所以3可以放到1后面，组成一个递增子序列。而且我们还知道dp[0] = 1，也就是说以nums[0] = 1这个元素结尾的最长递增子序列长度为1，我们把3放到这个子序列后面就可以组成一个长度为2的递增子序列，我们就暂时令dp[5] = dp[0] + 1=2；接着看nums[1] = 4，哎比3要大，没办法，下一个；下一个是nums[2] = 3，等于3，不行，递增子序列要求后一个比前一个要大，相等也不行，下一个；下一个是nums[3] = 4，同理不行，下一个；下一个是nums[4] = 2，比3要小，可以，我们可以把3放在这个2后面组成一个递增序列，又知道dp[4] = 2，所以前面以nums[4] = 2这个元素结尾的最长递增子序列长度为2，那也就是说，我们把3放到这个以nums[4] = 2为结尾的最长递增子序列后面可以得到一条长度加1的递增子序列，所以此时可以组成长度为dp[4] + 1 = 3的递增子序列。上一次在index = 0的时候，我们暂时令dp[5] = 2，到index = 4的时候，我们又发现nums[5] 可以和nums[4]组成长度为3的递增子序列，比之前的2更大了，所以我们重新令dp[5] = 3。

所以，这个题目中状态转移方程，需要遍历每一个前面各个位置来确定，看看当前的数可不可以和前面的数组成长度更长的递增子序列。

写出代码如下：

int maxIncreasingSubsequence(int[] nums){
    //确定一个dp数组，并给出其中元素的含义.
    //dp[i]的意义就是：以nums[i]为结尾的最长递增子序列的长度
    int[] dp = new int[nums.length];
    //设定初值,以nums[i]元素为结尾的最长递增子序列的长度最少是1
    Arrays.fill(dp,1);
    for(int i=0;i<dp.length;i++){
        for(int j=0;j<i;j++){
            //如果前面的一个数比当前数要小，说明当前的数可以放到前面
            //这个数后面组成递增子序列，我们看看能不能根据前面数的dp
            //值dp[j]来使得dp[i]变得更大。
            if(nums[j] < nums[i]){
                dp[i] = Math.max(dp[i],dp[j]+1);
            }
        }
    }
    //最后的结果就是dp中的最大值  
    int res = 0;
    for(int num : dp){
        res = Math.max(res,num);
    }  
    return res;
}

好了，其实你可以发现，这个题目用动态规划来做的话复杂度为O(n^2)，和暴力解法（我说，暴力解法你写出来没有？）复杂度一样，但是这并不说明动态规划就很垃圾，在大部分题目中，动态规划一般都可以把复杂度降为O(n)。

本月的直播，我将再讲几个动态规划的经典题目，相信大家如果了解的话，做935数据结构代码题就会多一种高效的让改卷老师眼前一亮的武器哦。

---

另外，其实这个题目还有一种O(nlogn)的解法，有兴趣的同学可以思考一下，具体的需要用到二分的变体，还记得吧，上上次直播咱们可都是讲了二分以及其所有变体的嘛

 

然后，要不咱们举一反三一下，稍微改一下这个题目：

已知一个int类型的数组nums,请求除nums的最长非递减子序列的长度。
例如：nums=[4,-1,2,2,2,3,-5,7,10]这个数组的最长非递减子序列就应该是
-1，2，2，2，3，7，10，而不再是-1，2，3，7，10了。所以此时应该返回7。
所以你们能不能想想如何用动态规划做呢？提示，只需要稍微修改一下上面求最长递增子序列的动态规划代码哦。