堆

堆是一种特殊的树，只要某棵树满足这两点，那么它就是树：

1.是一个完全二叉树。

2.该树的每个节点小于等于或者大于等于左右子树的所有节点的值，注意这不是像二叉查找树那种左小右大，而是要么左右都是小于等于，要么左右都是大于等于。、

 

小于等于的话叫做小顶堆，大于等于的话叫做大顶堆。

 

 

图中4不是堆，其他都是堆，我们可以看出同一组数据，可以组成出不同的堆。

 

如何实现一个堆

 既然我们知道了堆是一个完全二叉树，那么它的存储特性肯定也是和完全二叉树相同的，即可以用数组或链表来实现。

 为了节省内存，一般会用数组，所以下面以数组为例子来看看堆的插入和删除堆顶元素这两个核心操作

1.堆的插入

在插入了一个元素后，我们要做一些调整，以免堆的结构被破坏，这个过程叫做堆化。

如图，插入元素22后，由下往上，一个个比较，直到适合为止

 

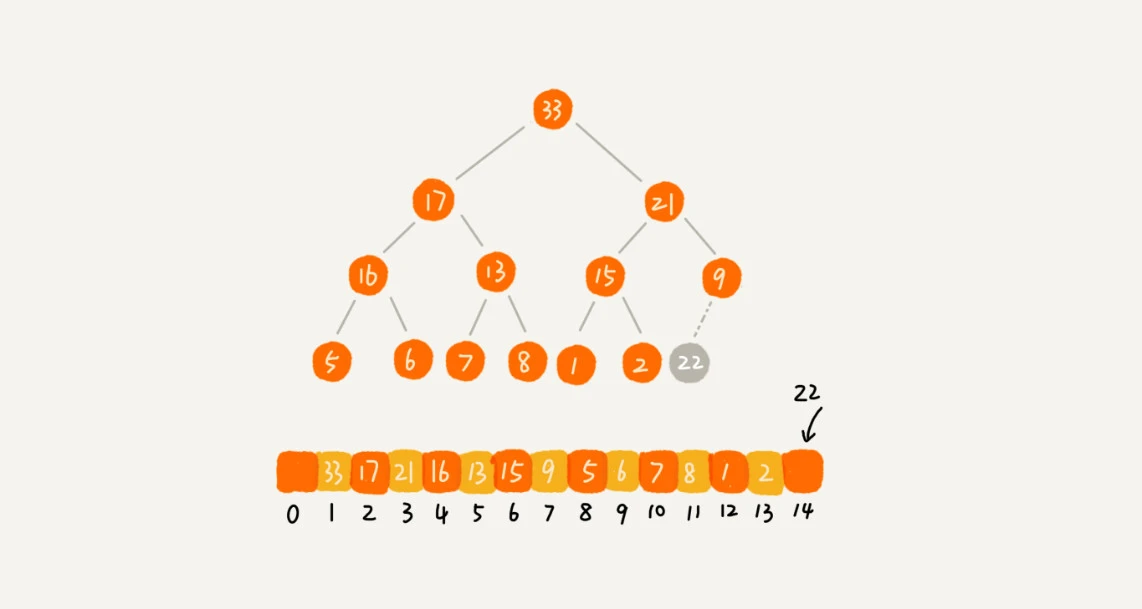
2.删除堆顶元素

删除堆顶元素的话，如果我们继续按照插入元素时那种从下到上的思路的话，那就是要把下面最小或者最大的元素提上来，而这种方法会出现问题，如图

 

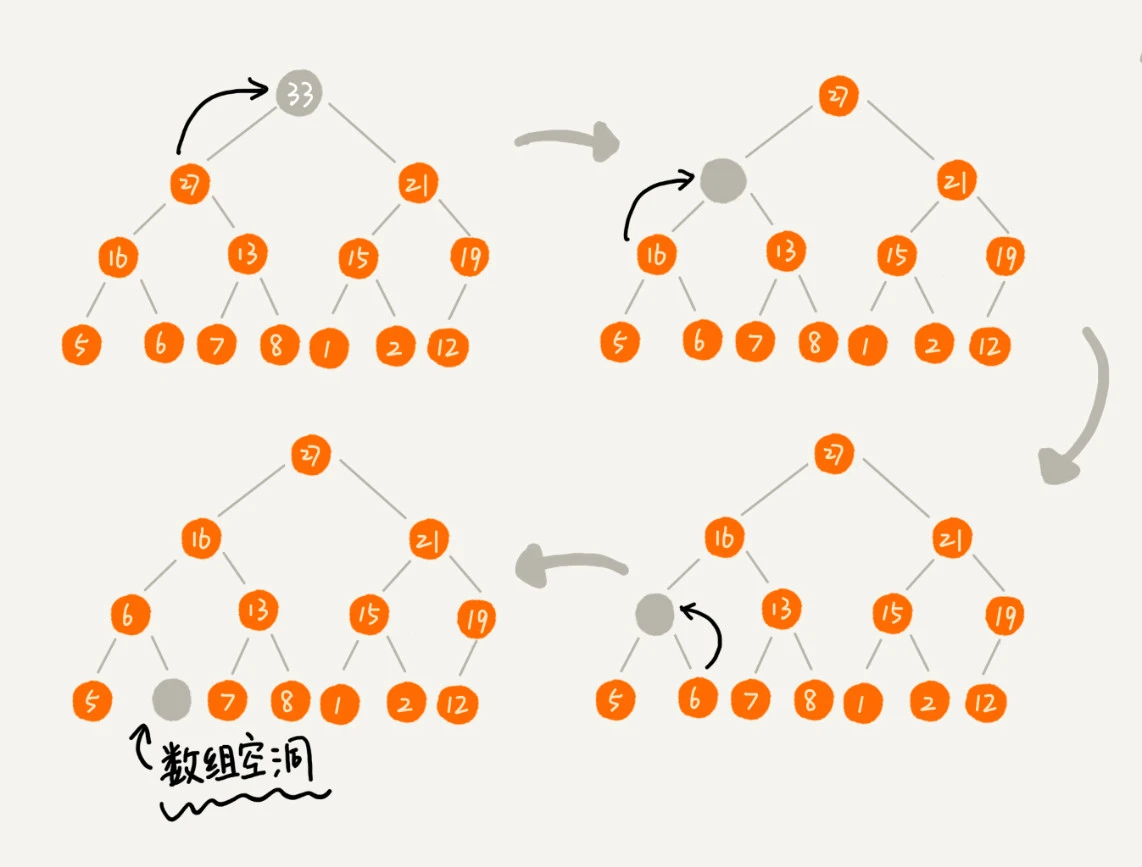
为了避免这个数组空洞，我们只需要换一种由上往下的思路即可

 

 

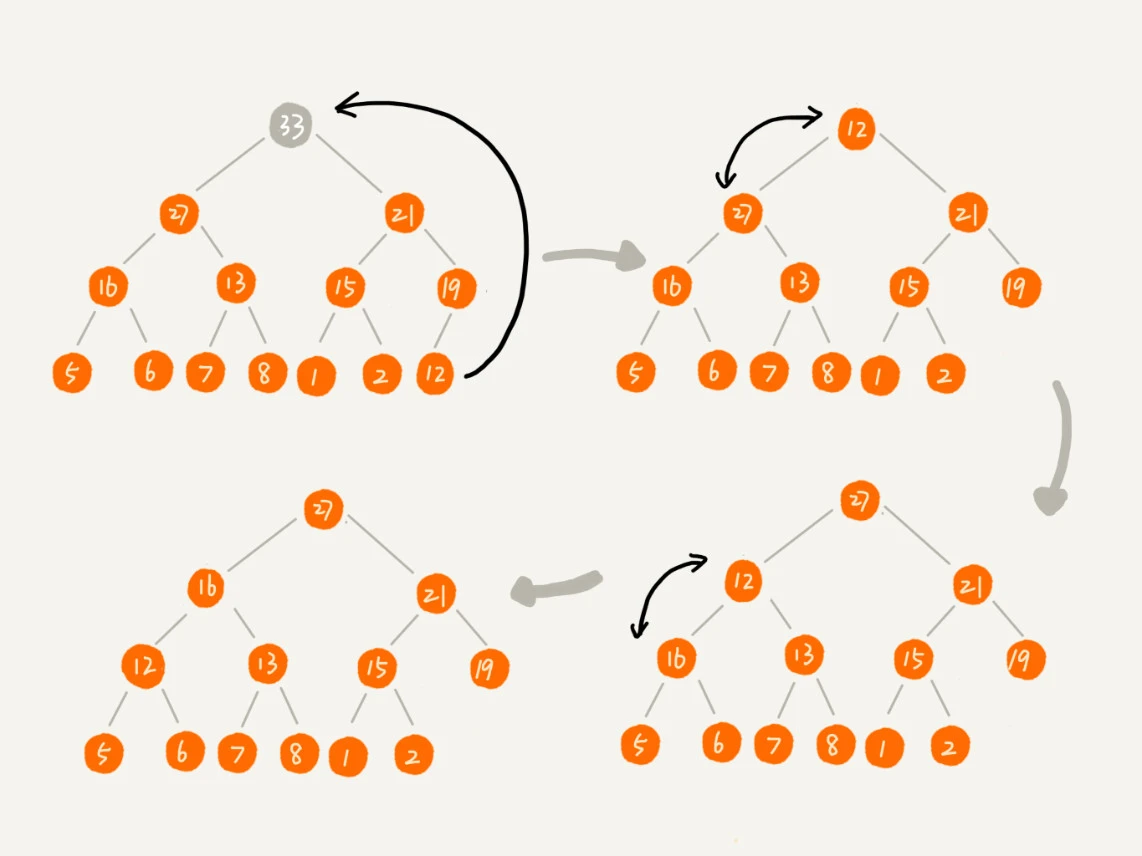
这里由于每次都是交换数组，所以不会出现空缺。

 

关于这两个操作：一个包含 n 个节点的完全二叉树，树的高度不会超过 log2​n。堆化的过程是顺着节点所在路径比较交换的，所以堆化的时间复杂度跟树的高度成正比，也就是 O(logn)。插入数据和删除堆顶元素的主要逻辑就是堆化，所以，往堆中插入一个元素和删除堆顶元素的时间复杂度都是 O(logn)。