排序

如何分析一个排序算法？

执行效率

①算出最好，最坏，平均时间复杂度，还要说出最好和最坏复杂度对应的原始数据是怎样的。 因为有些排序算法是进行了三个复杂度的区分，所以最好所有排序算法都进行区分，方便比较。

其次，要说出原始数据是因为有些原始数据非常无序，有些已经接近有序，有序度不同的数据，肯定会造成排序执行时间的影响，我们需要知道不同数据下，排序的性能表现。

 

②时间复杂度的常数，系数，低阶。因为排序时很多时候会遇到规模较小的数据，那么同阶的时间复杂度来说，常数，系数，低阶则不可忽略。

 

③比较次数和交换次数

 

内存消耗

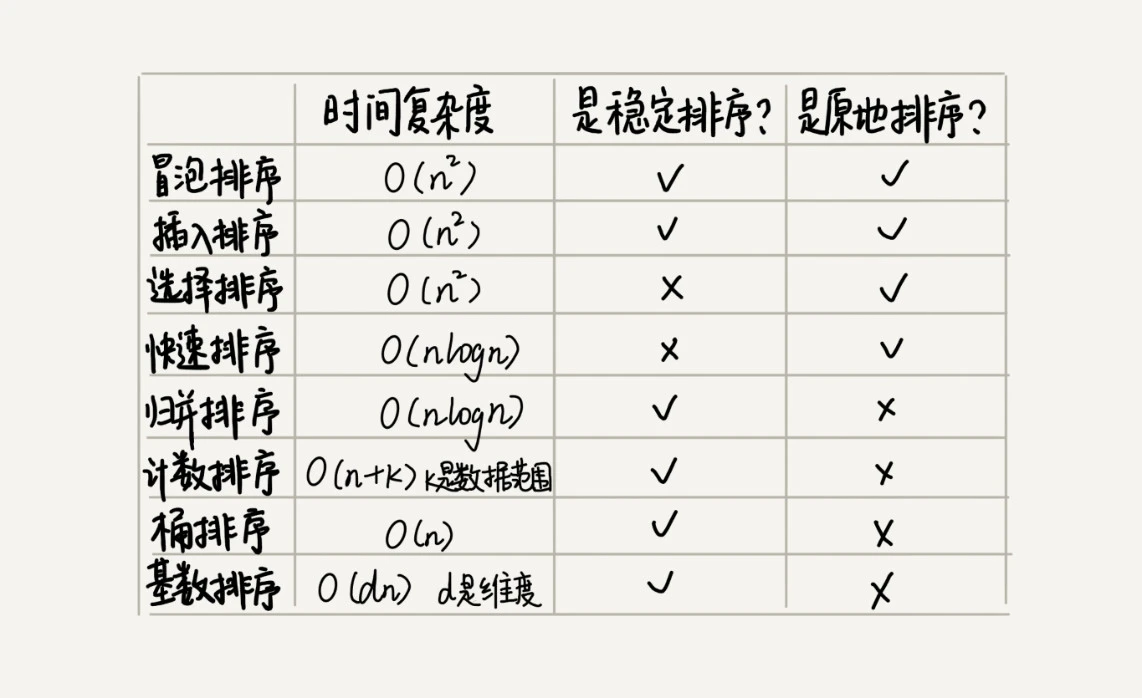
算法的内存消耗可以通过空间复杂度来衡量，排序算法也不例外。不过，针对排序算法的空间复杂度，我们还引入了一个新的概念，原地排序（Sorted in place）。原地排序算法，就是特指空间复杂度是 O(1) 的排序算法

 

排序算法的稳定性

这里的稳定性指的是：如果待排序的序列中存在值相等的元素，则排序后，值相等的元素先后顺序不变。

具有稳定性的排序算法叫做稳定排序算法，否则就是不稳定的排序算法。

可是，好像相等的元素之间先后顺序没任何意义，但我们要注意，排序的对象可能是键值对形式的，这时，用稳定排序就很有用了。

比如说，我们现在要给电商交易系统中的“订单”排序。订单有两个属性，一个是下单时间，另一个是订单金额。如果我们现在有 10 万条订单数据，我们希望按照金额从小到大对订单数据排序。对于金额相同的订单，我们希望按照下单时间从早到晚有序。对于这样一个排序需求，我们怎么来做呢？

最先想到的方法是：我们先按照金额对订单数据进行排序，然后，再遍历排序之后的订单数据，对于每个金额相同的小区间再按照下单时间排序。这种排序思路理解起来不难，但是实现起来会很复杂。借助稳定排序算法，这个问题可以非常简洁地解决。

解决思路是这样的：我们先按照下单时间给订单排序，注意是按照下单时间，不是金额。排序完成之后，我们用稳定排序算法，按照订单金额重新排序。两遍排序之后，我们得到的订单数据就是按照金额从小到大排序，金额相同的订单按照下单时间从早到晚排序的。

为什么呢？稳定排序算法可以保持金额相同的两个对象，在排序之后的前后顺序不变。第一次排序之后，所有的订单按照下单时间从早到晚有序了。在第二次排序中，我们用的是稳定的排序算法，所以经过第二次排序之后，相同金额的订单仍然保持下单时间从早到晚有序。

 

有序度和逆序度

 在计算排序的平均时间复杂度时，有时需要复杂的概率论知识来推导，这个不太好用，于是我们引出了有序度和逆序度的概念（这里有序指的是从小到大）

现在以数组这种数据结构为例

有序度：数组中具有有序关系的元素的个数，数学表达式如下

有序元素对： 如果i < j，a[i] <= a[j]。

 

逆序度：数组中不具有有序关系的元素的个数，数学表达式如下

逆序元素对： 如果i < j，a[i] > a[j],

 

满有序度：数组中所有元素都是有序的。计算公式：n*(n-1)/2

 

我们排序的过程就是一种增加有序度，减少逆序度的过程，最后达到满有序度，就说明排序完成了，即满有序度 = 有序度 + 逆序度。

 

几种常见的排序

 

 

插入排序

以数组为例，将数组分为已排区间和未排区间，每次在未排区间取一个，在已排区间里插入，直到未排区间为0。

如下图，左边是已排区间，右边是未排区间

 

这是一种稳定排序。

移动次数等于逆序度，因为对于一个确定的序列，满有序度不变，那么每移动一次就有序度+1，也即逆序度减一，直到逆序度为0，所以移动次数等于逆序度。

 

代码实现

// 插入排序，a表示数组，n表示数组大小
public void insertionSort(int[] a, int n) {
  if (n <= 1) return;

  for (int i = 1; i < n; ++i) {
    int value = a[i];
    int j = i - 1;
    // 查找插入的位置
    for (; j >= 0; --j) {
      if (a[j] > value) {
        a[j+1] = a[j];  // 数据移动
      } else {
        break;
      }
    }
    a[j+1] = value; // 插入数据
  }
}

 

冒泡排序和插入排序的时间复杂度都是 O(n2)，都是原地排序算法，冒泡排序不管怎么优化，元素交换的次数是一个固定值，是原始数据的逆序度。插入排序是同样的，不管怎么优化，元素移动的次数也等于原始数据的逆序度。为什么插入排序要比冒泡排序更受欢迎呢？

①从代码实现上来看，冒泡排序需要交换时需要赋值三次，插入排序只需要一次

冒泡排序中数据的交换操作：
if (a[j] > a[j+1]) { // 交换
   int tmp = a[j];
   a[j] = a[j+1];
   a[j+1] = tmp;
   flag = true;
}

插入排序中数据的移动操作：
if (a[j] > value) {
  a[j+1] = a[j];  // 数据移动
} else {
  break;
}

 

我们把执行一个赋值语句的时间粗略地计为单位时间（unit_time），然后分别用冒泡排序和插入排序对同一个逆序度是 K 的数组进行排序。用冒泡排序，需要 K 次交换操作，每次需要 3 个赋值语句，所以交换操作总耗时就是 3*K 单位时间。而插入排序中数据移动操作只需要 K 个单位时间。

而且插入排序还可以用希尔排序更深一步优化，所以如果希望性能尽量高，首选插入排序

 

选择排序

也是分开已排区间和未排区间，但选择排序是每次在未排区间中选出最小的数，加到已排区间的末尾

 

 

选择排序是不稳定的排序算法

 

 

冒泡排序、插入排序、选择排序这三种排序算法，它们的时间复杂度都是 O(n2)，比较高，适合小规模数据的排序。现在，两种时间复杂度为 O(nlogn) 的排序算法，归并排序和快速排序。这两种排序算法适合大规模的数据排序

 

归并排序

归并排序的核心思想还是蛮简单的。如果要排序一个数组，我们先把数组从中间分成前后两部分，然后对前后两部分分别排序，再将排好序的两部分合并在一起，这样整个数组就都有序了。

 

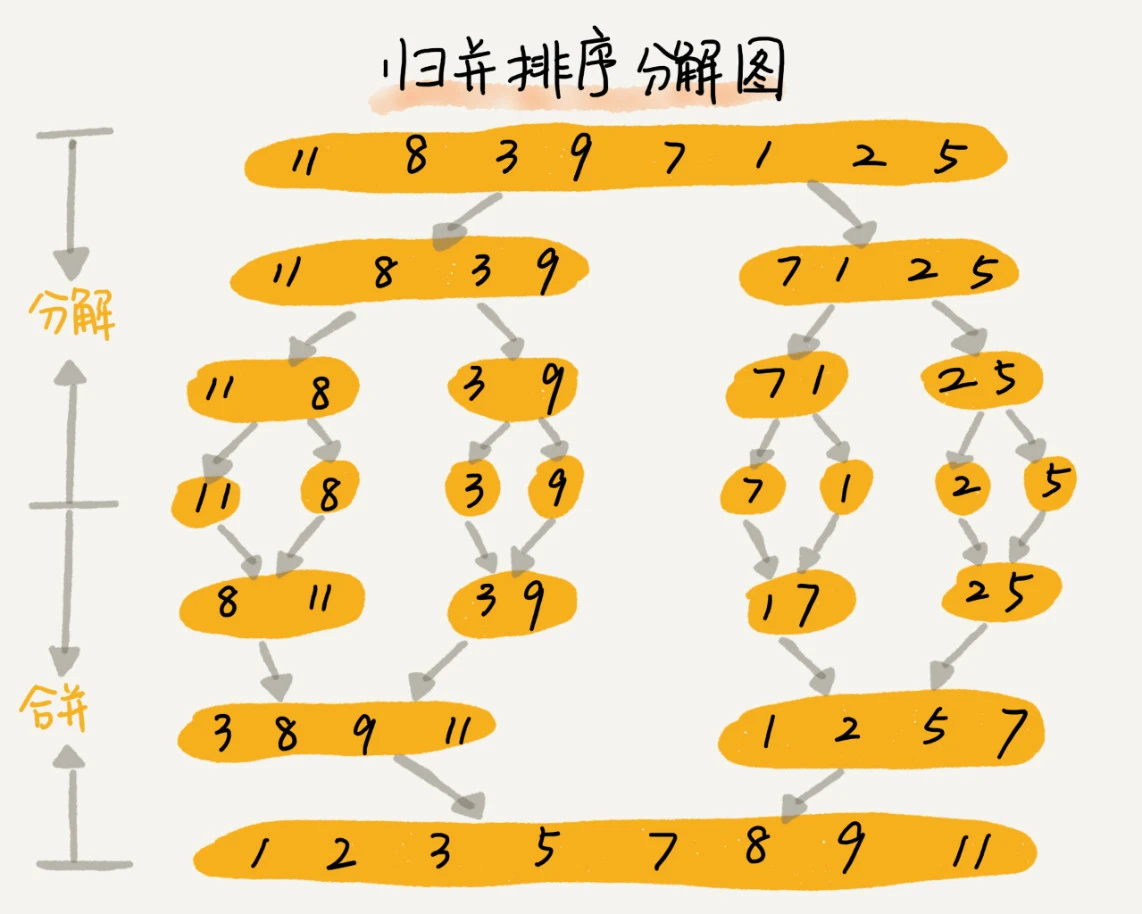
举个例子

class MergeSort {
    public void mergeSortTarget(int[] arr) {
        mergeSort(arr, 0, arr.length - 1);
    }

    public static void mergeSort(int[] arr, int head, int tail) {
        //递归终止条件
        if (head >= tail) {
            return;
        }

        //间隔点
        int breakPoint = head + (tail - head) / 2;
        //左边的区间
        mergeSort(arr, head, breakPoint);
        //右边区间
        mergeSort(arr, breakPoint + 1, tail);
        merge(arr,head,breakPoint,tail);
    }

    public static void merge(int[] arr,int head,int breakPoint,int tail){
        //合并两个区间
        //先弄一个临时数组
        int[] temp = new int[tail - head + 1];
        //左右区间的游标
        int left = head;
        int right = breakPoint + 1;
        //temp的下标
        int index = 0;

        //左游标指向的元素和右游标指向的元素比较
        //谁小谁就进入temp
        while (left <= breakPoint && right <= tail) {
            if (arr[left] <= arr[right]) {
                temp[index++] = arr[left++];
            } else {
                temp[index++] = arr[right++];
            }
        }

        //判断哪个区间还有剩余
        //这时假设left --- breakPoint有剩余
        //如果right <= tail
        int start = left,end = breakPoint;
        if (right <= tail){
            start  = right;
            end = tail;
        }

        //把剩余的放进temp
        while (start <= end){
            temp[index++] = arr[start++];
        }

        //把temp数组的数据复制回给原数组
        //这里arr[head + i],如果是arr[i],那每层递归都会从arr[0]开始赋值
        //所以我们用arr[head + i]可以从我们当前的小区间的头部开始赋值，
        // 而且本来处理的也只是这个小区间的数据，而不是从头到尾，整个arr
        for (int i = 0; i <= tail - head; i++) {
            arr[head + i] = temp[i];
        }
    }

}

 

归并排序的原理其实和递归差不多，代码的实现也是使用递归

归并排序不是稳定排序，并且不是原地排序，空间复杂度为O（n）

 

 

快速排序

如果要排序数组，我们把其中一个元素定位pivot，然后遍历数组，把大于pivot的和小于pivot的分别堆到pivot的两边

 

 

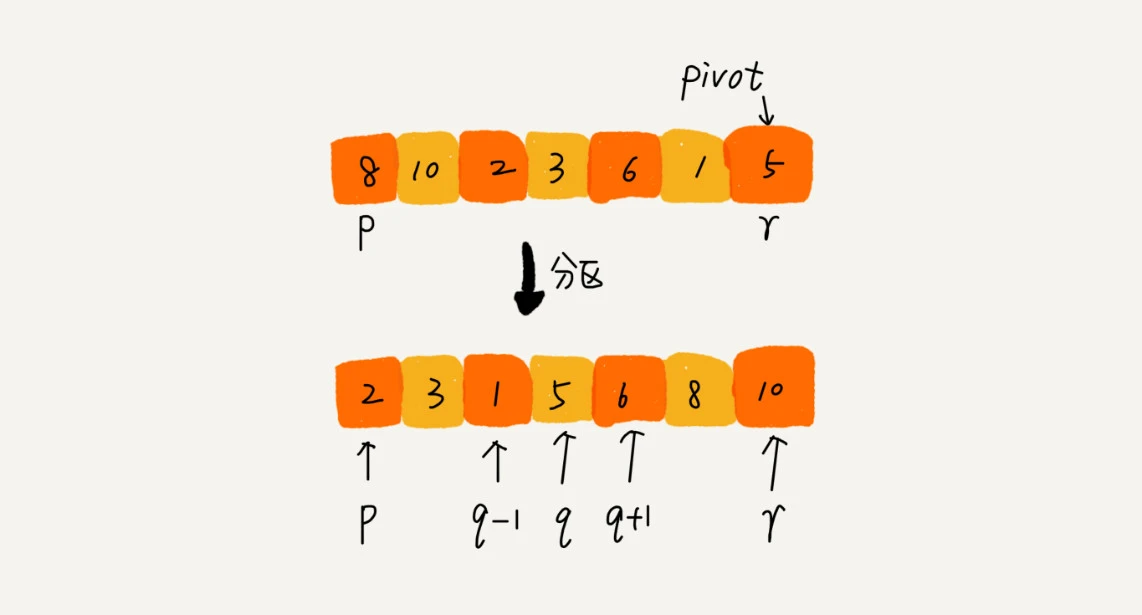
这样，当左边区间的最右端和右边区间的最左端下标差值为1时，就排序成功，pivot在中间

 

举个例子

class QuickSort {

    public void quickSortTarget(int[] arr) {
        quickSort(arr, 0, arr.length - 1);
    }

    public void quickSort(int[] arr, int head, int tail) {
        //递归终止条件
        if (head >= tail)
            return;

        //分区点
        int pivot = partition(arr, head, tail);
        //快排是先弄大问题再弄子问题，所以不需要合并函数来整合
        //注意不要把分区点加上去，分区点是独立出来的
        //因为不同于归并，快排的分区点的左右两个区间
        //是以分区点为基准来排的，所以分区点对这两个区间是有序的
        //比如这段排序成从小到大的代码里，左区间中pivot必定最大，右区间中pivot必定最小
        //所以不用参与这两个区间的下一级排序，没必要而且还浪费时间
        quickSort(arr, head, pivot - 1);
        quickSort(arr, pivot + 1, tail);
    }

    //用这个函数来实现排序，这个函数可以不需要额外占用很多内存空间
    //名叫原地分区函数
    public int partition(int[] arr, int head, int tail) {
        //以最后一个元素为pivot
        int pivot = arr[tail];

        //以pivot基准来排序
        //定义两个游标，左游标左边是已排好的，小于pivot的
        //右游标遍历整条小区间，直到右游标指向pivot
        //然后将pivot和i指向的交换
        int left = head;

        for (int right = head; right < tail; right++) {
            if (arr[right] < pivot) {
                int temp = arr[left];
                arr[left] = arr[right];
                arr[right] = temp;
                left++;
            }
        }

        int temp = arr[left];
        arr[left] = arr[tail];
        arr[tail] = temp;

        //此时left就是分区点
        return left;
    }
}

 

这段代码原理是这样的

 

 

 

 

 

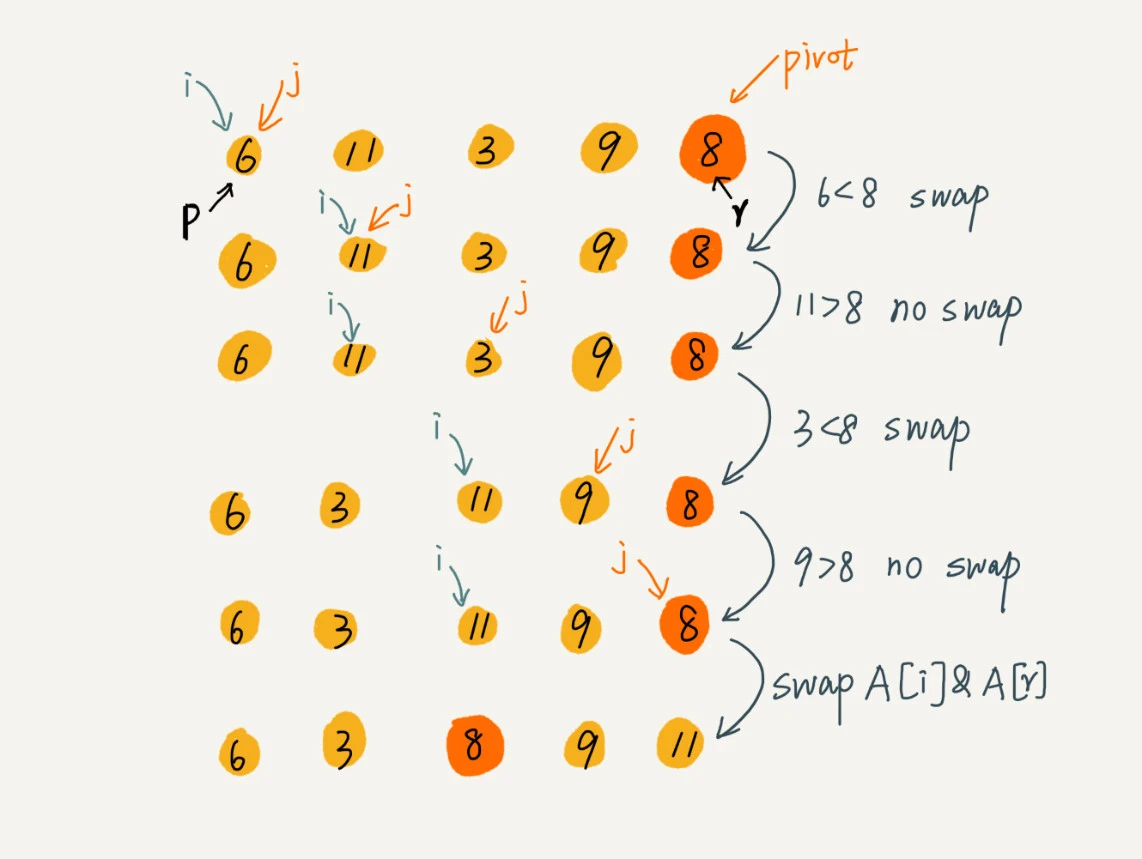
快速排序和归并排序的区别

 

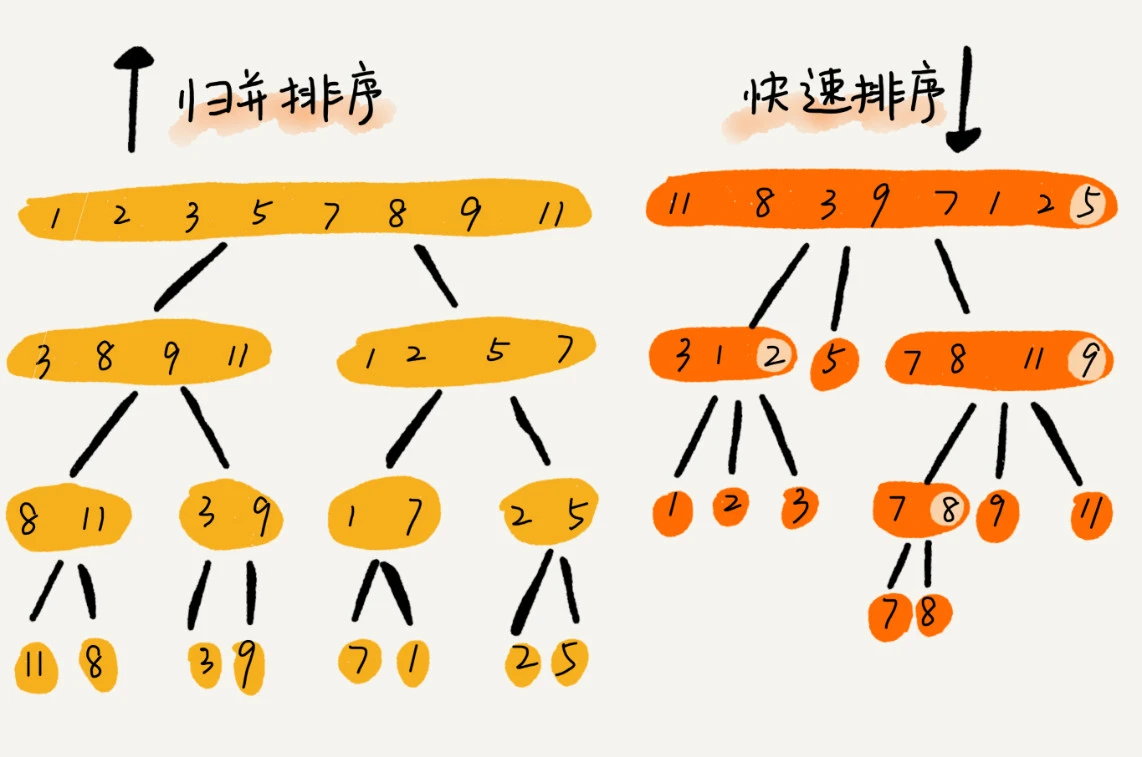
归并是从下到上解决问题的，快排是从上到下

 

堆排序

我们可以把堆排序的过程大致分解成两个大的步骤，建堆和排序。

1. 建堆我们首先将数组原地建成一个堆。所谓“原地”就是，不借助另一个数组，就在原数组上操作。建堆的过程，有两种思路。

第一种是借助我们前面讲的，在堆中插入一个元素的思路。尽管数组中包含 n 个数据，但是我们可以假设，起初堆中只包含一个数据，就是下标为 1 的数据。然后，我们调用前面讲的插入操作，将下标从 2 到 n 的数据依次插入到堆中。这样我们就将包含 n 个数据的数组，组织成了堆。

第二种实现思路，跟第一种截然相反，也是我这里要详细讲的。第一种建堆思路的处理过程是从前往后处理数组数据，并且每个数据插入堆中时，都是从下往上堆化。而第二种实现思路，是从后往前处理数组，并且每个数据都是从上往下堆化。我举了一个例子，并且画了一个第二种实现思路的建堆分解步骤图，你可以看下。因为叶子节点往下堆化只能自己跟自己比较，所以我们直接从最后一个非叶子节点开始，依次堆化就行了。

第二种如图

 

 

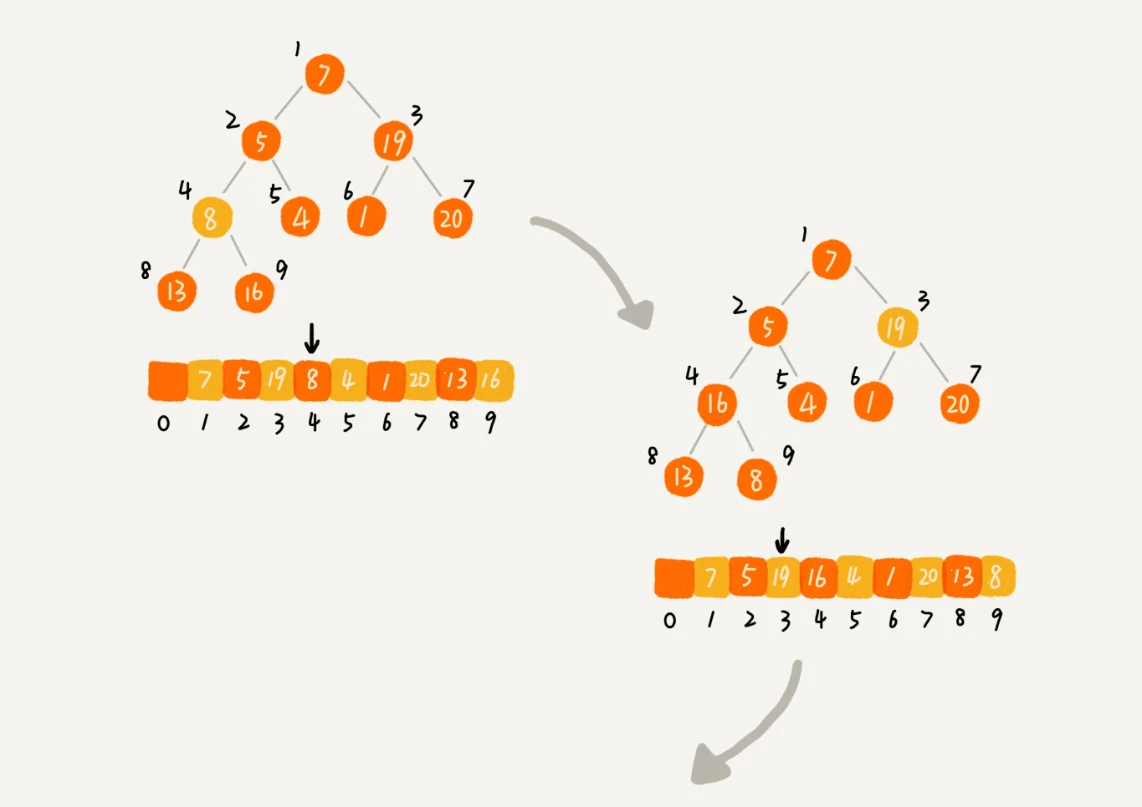
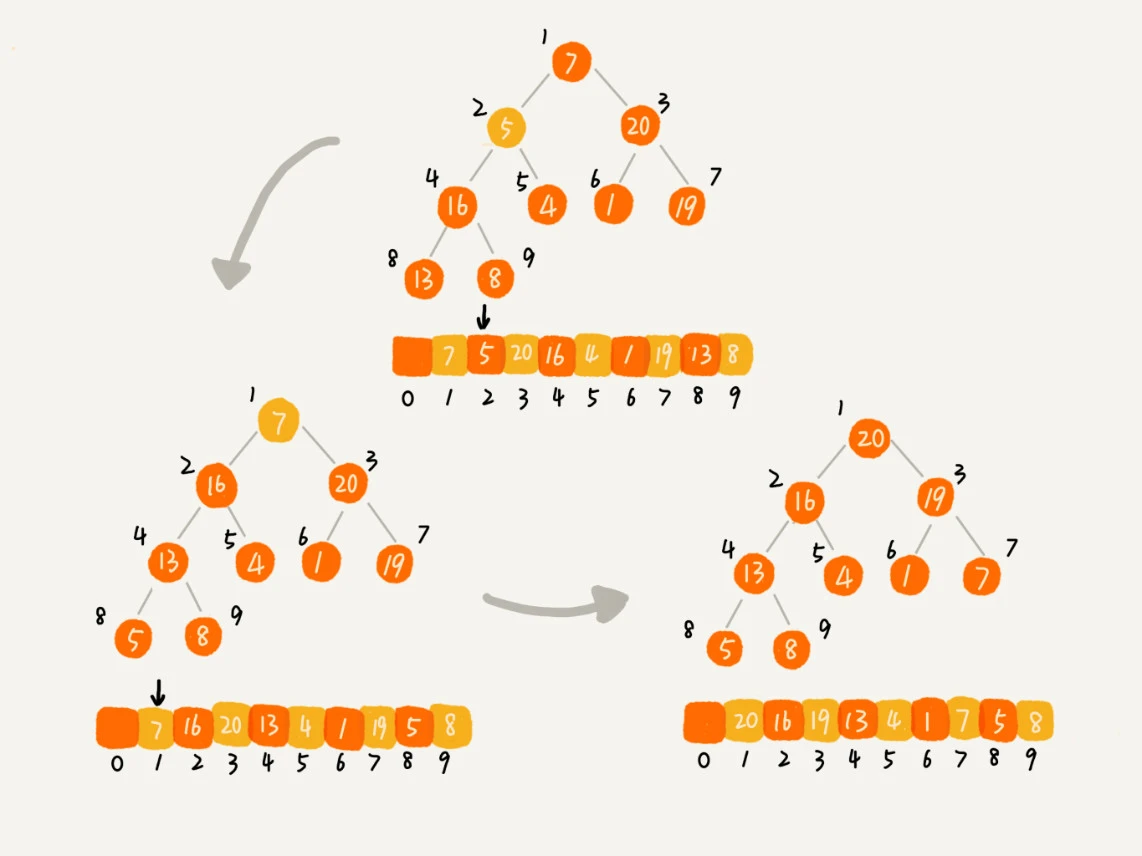
private static void buildHeap(int[] a, int n) {
  for (int i = n/2; i >= 1; --i) {
    heapify(a, n, i);
  }
}

private static void heapify(int[] a, int n, int i) {
  while (true) {
    int maxPos = i;
    if (i*2 <= n && a[i] < a[i*2]) maxPos = i*2;
    if (i*2+1 <= n && a[maxPos] < a[i*2+1]) maxPos = i*2+1;
    if (maxPos == i) break;
    swap(a, i, maxPos);
    i = maxPos;
  }
}

 

建堆的时间复杂度，粗算的话是O（nlogn），细算的话，是O（n）。

 

2.排序

堆结束之后，数组中的数据已经是按照大顶堆的特性来组织的。数组中的第一个元素就是堆顶，也就是最大的元素。我们把它跟最后一个元素交换，那最大元素就放到了下标为 n 的位置。这个过程有点类似上面讲的“删除堆顶元素”的操作，当堆顶元素移除之后，我们把下标为 n 的元素放到堆顶，然后再通过堆化的方法，将剩下的 n−1 个元素重新构建成堆。堆化完成之后，我们再取堆顶的元素，放到下标是 n−1 的位置，一直重复这个过程，直到最后堆中只剩下标为 1 的一个元素，排序工作就完成了。

 

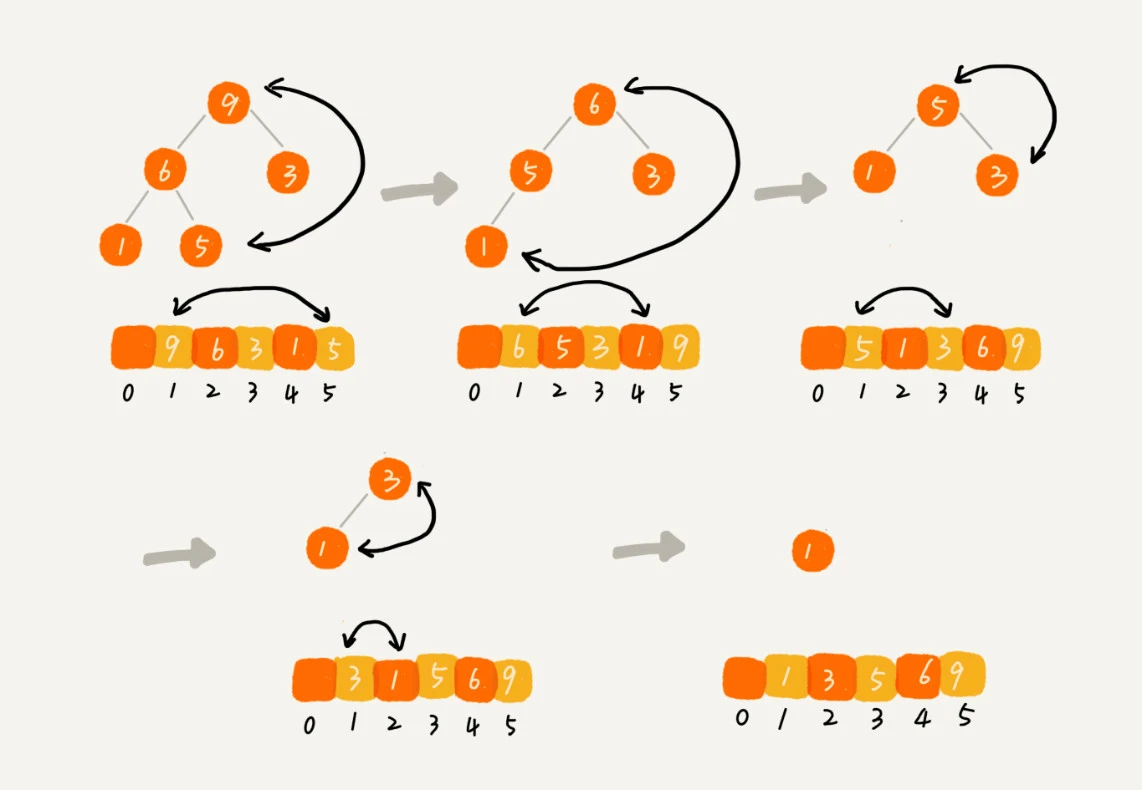
由于要进行n次这样的操作，而每次操作时交换操作时常量操作，那么时间复杂度相当于只有排序的O（logn）复杂度，也就是排序时O（nlogn）复杂度。

所以整个堆排序时间复杂度是O（n（1 + logn）） == O（nlogn）

 

堆排序不是稳定的排序算法，因为在排序的过程，存在将堆的最后一个节点跟堆顶节点互换的操作，所以就有可能改变值相同数据的原始相对顺序。

 

在实际开发中，为什么快速排序要比堆排序性能好？

第一点，堆排序数据访问的方式没有快速排序友好。对于快速排序来说，数据是顺序访问的。而对于堆排序来说，数据是跳着访问的。 比如，堆排序中，最重要的一个操作就是数据的堆化。比如下面这个例子，对堆顶节点进行堆化，会依次访问数组下标是 1，2，4，8 的元素，而不是像快速排序那样，局部顺序访问，所以，这样对 CPU 缓存是不友好的。

 

第二点，对于同样的数据，在排序过程中，堆排序算法的数据交换次数要多于快速排序。我们在讲排序的时候，提过两个概念，有序度和逆序度。对于基于比较的排序算法来说，整个排序过程就是由两个基本的操作组成的，比较和交换（或移动）。快速排序数据交换的次数不会比逆序度多。但是堆排序的第一步是建堆，建堆的过程会打乱数据原有的相对先后顺序，导致原数据的有序度降低。比如，对于一组已经有序的数据来说，经过建堆之后，数据反而变得更无序了。