二分查找

二分查找，简单来说就是在给定的数据范围，每次取完中间数后，就二分缩小范围（范围的最小值或者最大值，其中一个变成前一次范围的中间值），直到范围区间只有一个数或者找到想要的数。

 

举个例子

我们假设只有 10 个订单，订单金额分别是：8，11，19，23，27，33，45，55，67，98。还是利用二分思想，每次都与区间的中间数据比对大小，缩小查找区间的范围。为了更加直观，我画了一张查找过程的图。其中，low 和 high 表示待查找区间的下标，mid 表示待查找区间的中间元素下标。

 

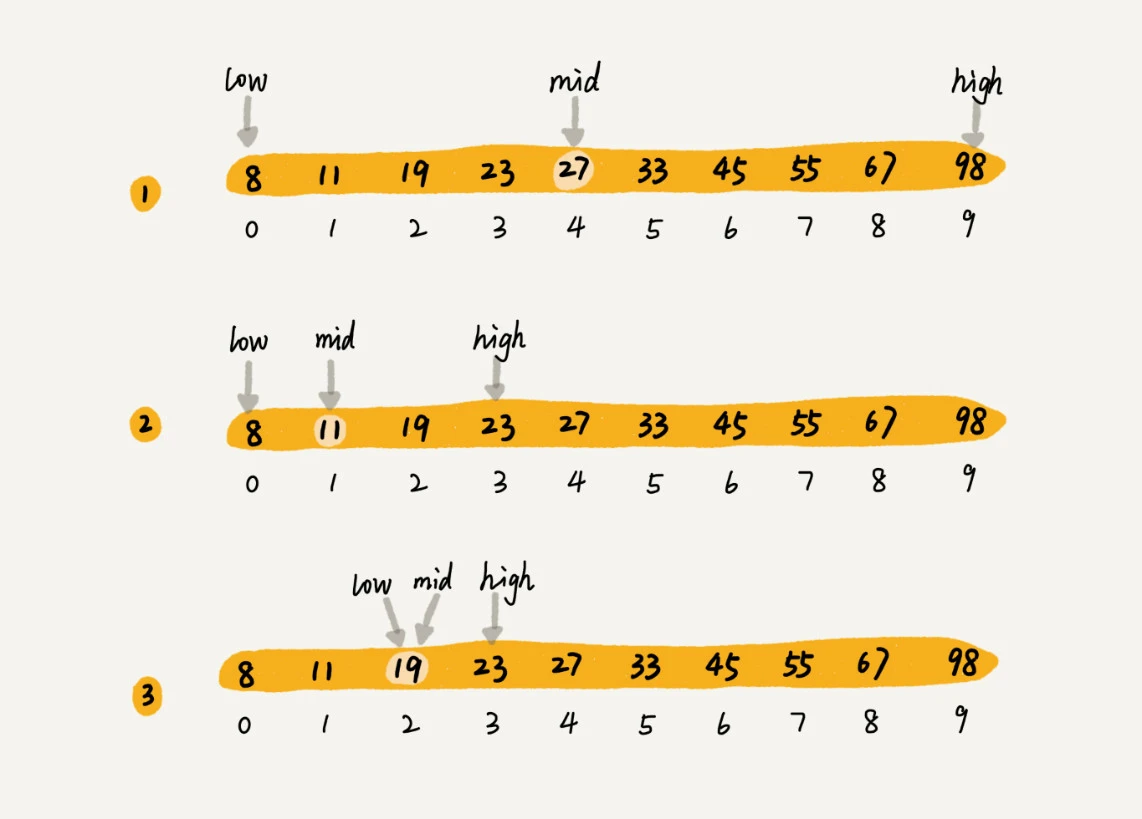
注意，二分查找针对的是一个有序的数据集合，查找思想有点类似分治思想。

 

 

二分查找的时间复杂度

二分查找速度非常快，我们假设被查找的数据总数为n，那么区间变化如下

 

最后的数的k，表示一共二分了k次，并且每次只涉及区间开端和末端与中间数的大小比较，所以时间复杂度是O（k），再通过指数与对数的转换式，得出O（k） = O（logn），所以二分查找的时间复杂度是O（logn）

O（logn）是一种非常高效的算法，高效到当常量级时间复杂度比较大时，O（logn）比O（1000），O（10000）等等更高效

而且，指数有一个经典的名词，叫做指数爆炸，这是因为随着次方的提升，指数会增长得非常快，而对数对应着指数，即便指数数值非常大，由于对数的值是次方，那么对数的值也不会很大

所以当二分查找要查找的范围很大，比如2的64次方，即18446744073709551616，也只最多只需要64次就找到了想要的数据，真的恐怖

 

注意，还可以用递归来实现二分查找

public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;

  while (low <= high) {
    int mid = (low + high) / 2;
    if (a[mid] == value) {
      return mid;
    } else if (a[mid] < value) {
      low = mid + 1;
    } else {
      high = mid - 1;
    }
  }

  return -1;
}

 

 

二分查找注意事项

先举个最简单的代码

public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;

  while (low <= high) {
    int mid = low + (high - low) >> 1;if (a[mid] == value) {
      return mid;
    } else if (a[mid] < value) {
      low = mid + 1;
    } else {
      high = mid - 1;
    }
  }

  return -1;
}

 

①当low == high时仍需要进行查找，因为这时唯一的那个数也不一定就是我们所查找的value。

 

②mid的取值不能是直接(low + high) / 2,因为int类型最大表示范围是2147483647，如果输入的low和high都接近2147483647，两个数相加就会溢出，变成一个负数。所以我们要拿另一条算式

　low + (high - low) >> 1，这条算式不但算的结果和(low + high) / 2，而且还防止了溢出，推理过程：（low+high)/2=(2*low+high-low)/2=(2*low)/2+(high-low)/2=low+(high-low)/2

 

③注意更新low和hig要加减1，否则可能死循环，比如当low == high ，并且a[low]  != value,那么一直都不能退出循环

 

二分查找的应用场景

二分查找其实局限性挺大。

首先，二分查找依赖于数组，因为他是需要随机下标来访问元素，否则的话会很慢，你要是像链表，那么第一次要移动n/2才能找到中间值，第二次再除以二，移动n/4,第三次再除以二，移动n/8才能找到中间值，而数组使用的是偏移公式，一步到位访问到中间值。

 

然后就是数据太小或者太大都不适合二分查找。

如果数据量太小，比如就五个元素，那么你二分和遍历数组没什么区别，除非你的每个元素是类似于几百个，几千个字的字符串这种数据之间的比较操作很费时间的情况。

如果数据量太大，可能会没有合适的内存空间来给数组分配空间，因为数组一定是连续的内存空间，要是内存空间很零散，很多碎片，那你的数组就分配不下来了。

 

最后注意，二分查找是针对有序的数据才好用，对于无序的数据集合，如果是静态的还好，弄一次排序就行，可以均摊，但要是动态的就不行了，因为每次进行插入和删除，都要重新排序，导致时间成本的大大提升

实际上，二分查找除了用循环来实现，还可以用递归来实现，过程也非常简单。