时间空间复杂度分析
时间空间复杂度是衡量代码执行效率的一个重要指标。
事后统计法依赖于测试环境,会受极端数据规模的影响,所以时间空间复杂度分析就应运而生了
大O时间复杂度表示法
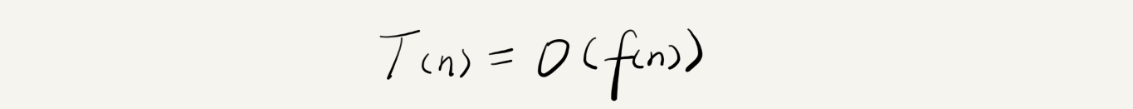
T(n)代表代码执行的时间,f(n)代表每行代码执行次数的总和,O是代表前面两个变量成正比,n是数据规模
大O时间复杂度实际上并不代表代码具真正运行的时间,而是代表代码执行时间随数据规模增长的变化趋势,所以也叫渐进时间复杂度,简称时间复杂度
时间复杂度的分析
①只关注执行次数最多的一段代码,因为左右变化趋势的都是最高阶n的代码,n越大,这段代码造成的时间变化趋势就越大,常量趋势固定,不能左右趋势,而低阶的n比起最高阶的n,也是不能左右趋势的,所以n要取程序中执行次数最多的代码的执行次数
所以我们可以得出运算律:
加法法则:总的时间复杂度等于量级最大的那段代码的复杂度
抽象成公式就是:如果 T1(n)=O(f(n)),T2(n)=O(g(n));那么 T(n)=T1(n)+T2(n)=max(O(f(n)), O(g(n))) =O(max(f(n), g(n))).
乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
抽象成公式:如果 T1(n)=O(f(n)),T2(n)=O(g(n));那么 T(n)=T1(n)*T2(n)=O(f(n))*O(g(n))=O(f(n)*g(n)).
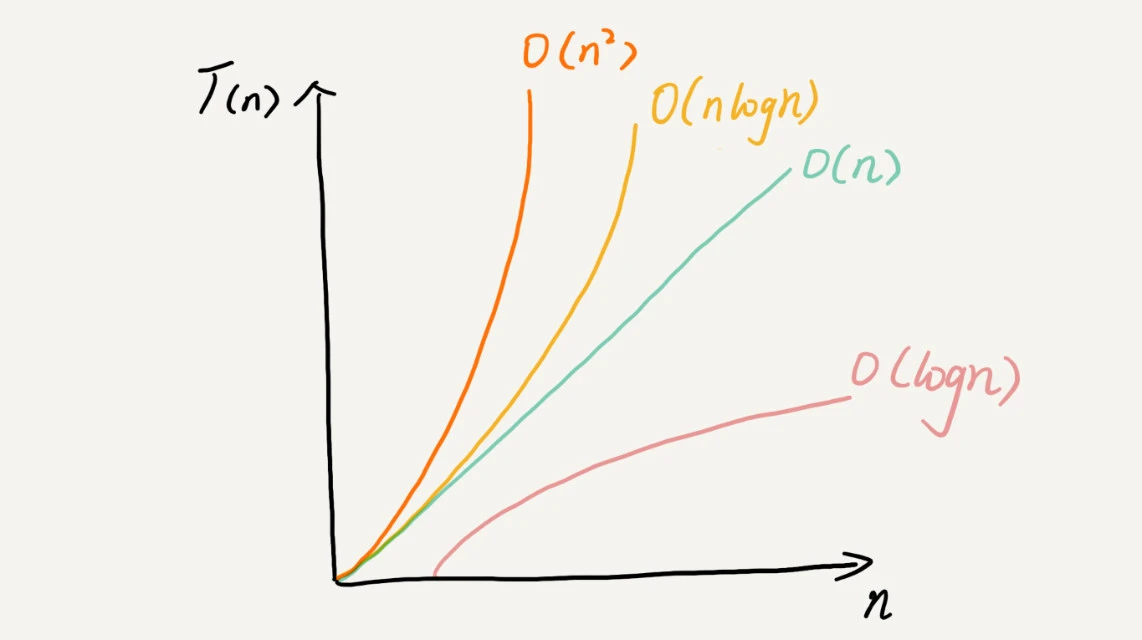
几种常见的时间复杂度实例分析

这些复杂度量级可以粗略分为两类:多项式量级和非多项式量级,其中非多项式量级只有指数阶和阶乘阶
对于非多项式量级的算法问题叫做NP(Non-Deterministic Polynomial,非确定多项式)问题,当数据规模越来越大时,非多项式算法的执行时间会急剧增加,求解问题需要的耗时会无限增长,所以非多项式时间复杂度的算法,其实是非常低效的算法,是垃圾代码
O(1)
这是常量时间复杂度,代码执行时间不会因n变化而变化
O(logn)、O(nlogn)
很常见且最难分析的一种,一般当数据规模呈等比数列或是其他能构成对数形式时用。
i=1; while (i <= n) { i = i * 2; }
这段代码,每次i的取值其实就是前一次的值乘2,所以所有i的取值是一个公比为2的等比数列,并且最后一次的i值就是执行次数,所以n=O(logn)
注意:不管是以 2 为底、以 3 为底,还是以 10 为底,我们可以把所有对数阶的时间复杂度都记为 O(logn)。为什么呢?我们知道,对数之间是可以互相转换的,log3n 就等于 log32 * log2n,所以 O(log3n) = O(C * log2n),其中 C=log32 是一个常量。基于我们前面的一个理论:在采用大 O 标记复杂度的时候,可以忽略系数,即 O(Cf(n)) = O(f(n))。所以,O(log2n) 就等于 O(log3n)。因此,在对数阶时间复杂度的表示方法里,我们忽略对数的“底”,统一表示为 O(logn)
O(m+n)、O(m*n)
这其实是加法法则的一种特殊情形,当我们无法比较m和n谁的量级大时,就要把加法法则改成这样:T1(m) + T2(n) = O(f(m) + g(n)),乘法法则不变
有时候,代码在不同的情况有不同的复杂度,于是有了最好情况时间复杂度,最坏情况时间复杂度,平均情况时间复杂度
最好情况时间复杂度:在最理想的情况下,执行这段代码的时间复杂度
最坏情况时间复杂度:在最糟糕的情况下,执行这段代码的时间复杂度
平均情况时间复杂度:在概率期望值的情况下,执行这段代码的时间复杂度,也叫加权平均时间复杂度或期望时间复杂度
还有一种更高级的概念
均摊时间复杂度,其分析方法是摊还分析,或者叫平摊分析,这算是平均情况时间复杂度的一种特殊情形
应用场景比较特殊:对一个数据结构进行一组连续操作中,大部分情况下时间复杂度都很低,只有个别情况下时间复杂度比较高,而且这些操作之间存在前后连贯的时序关系,这个时候,我们就可以将这一组操作放在一块儿分析,看是否能将较高时间复杂度那次操作的耗时,平摊到其他那些时间复杂度比较低的操作上。而且,在能够应用均摊时间复杂度分析的场合,一般均摊时间复杂度就等于最好情况时间复杂度。
空间复杂度
空间复杂度全称渐进空间复杂度,表示算法的存储空间与数据规模之间的增长关系,原理类似于时间复杂度
总之,越高阶复杂度的算法,执行效率越低



 浙公网安备 33010602011771号
浙公网安备 33010602011771号