第8章排序

第8章排序

8.1 基本概念和排序方法概述

8.1.1排序概念

（1）定义

排序（Sorting）是将一组杂乱无章的数据，按照预先设定的规则（如数值大小、字母顺序等）排列成有序序列的过程。

• 排序规则：常见为 “升序”（自小到大，如 08→16→21）或 “降序”（自大到小，如 49→25→21），只要最终序列满足 “有序” 即可。

• 重复元素的处理：

  若序列中存在相同关键字（如 “08,16,21,25,25”），为区分两个 “25”（视为不同数据对象），通常在后续重复元素后加 “” 标记（即 “25,25”）。此标记的核心作用是后续判断 “稳定性” 时，能明确相同关键字的原始先后次序。

  示例：无序序列[08,21,16,25*,25]，升序排序后为[08,16,21,25,25*]（若稳定）或[08,16,21,25*,25]（若不稳定），通过标记可直观观察次序变化。

8.1.2排序方法的分类

课堂与课件一致，排序方法可从 “规则”“时间复杂度” 两个核心维度分类，具体类别及子类如下（修正课堂识别错误：“C2 插入排序” 实际为 “希尔排序”）：

（1）分类维度

分类维度	具体划分
按排序规则	升序排序、降序排序（根据业务需求选择）
按时间复杂度	- 简单排序：时间复杂度为O(n²)（适用于小规模数据） - 高效排序：时间复杂度为O(nlog₂n)或更低（适用于大规模数据）

（2）具体类别及子类（核心框架）

排序算法主要分为五大类，每类包含典型子类，需明确对应关系：

大类	包含子类	时间复杂度范围	适用场景
插入排序	直接插入排序、折半（二分）插入排序、希尔排序（课堂 “C2 插入” 修正）	O(n²)（前两者）、O(n¹.³)（希尔）	小规模数据（前两者）、中规模数据（希尔）
交换排序	冒泡排序、快速排序	O(n²)（冒泡）、O(nlog₂n)（快速）	小规模（冒泡）、大规模（快速，平均情况）
选择排序	直接选择排序、树形选择排序、堆排序	O(n²)（直接选择）、O(nlog₂n)（堆排序）	小规模（直接选择）、大规模（堆排序）
归并排序	二路归并排序、多路归并排序	O(nlog₂n)	大规模数据（需稳定排序时优先）
分配排序	多关键字排序、基数排序（课堂补充的 “第五类”）	O(d(n+r))（d 为关键字位数，r 为基数）	整数、字符串等可按 “位” 排序的数据

• 初始分类为 “插入、交换、选择、归并” 四大类，后续补充 “分配排序”（含基数排序），形成完整的五大类框架；
• 时间复杂度是区分 “简单排序” 与 “高效排序” 的核心：O(n²)算法实现简单但效率低，O(nlog₂n)算法效率高但逻辑稍复杂。

8.1.3排序方法的核心评价指标

判断一个排序算法优劣，需从时间效率、空间效率、稳定性三个维度综合衡量，课堂对每个维度均做了重点解释：

（1）时间效率：排序速度的核心

• 定义：指算法执行过程中关键操作的次数，核心关键操作为 “关键字比较” 和 “数据对象移动”（强调：这两个操作是排序的核心消耗）。
• 影响因素：与数据规模n、数据初始排列状态相关（如 “已基本有序” 和 “完全无序” 对冒泡排序的效率影响极大）。
  • 示例（课堂隐含）：对n=6的序列[17,3,25,14,20,9]，直接插入排序在 “已升序” 时（最好情况），比较次数仅5次（n-1）、移动次数0；若 “完全降序”（最坏情况），比较次数为15次（n(n-1)/2）、移动次数更多。

（2）空间效率：辅助空间的消耗

• 定义：指算法执行过程中，除原始数据存储外，额外申请的辅助空间大小（课堂表述：“辅助空间的申请，它占空间有多大”）。
• 常见场景：
  • 低空间消耗：如直接插入排序、冒泡排序，仅需 1 个临时变量存储待插入 / 交换元素，空间复杂度为O(1)；
  • 高空间消耗：如归并排序，需额外申请与原始数组大小相同的辅助数组，空间复杂度为O(n)。

（3）稳定性：相同关键字的次序保持

• 定义（课堂通俗解释）：若序列中存在两个关键字相同的数据对象（如 A 的关键字 = B 的关键字，且原始序列中 A 在 B 之前），排序后仍能保持 “A 在 B 之前”，则称该算法 “稳定”；否则 “不稳定”。

• 课堂示例验证：

  以序列[25（A）,25*（B）,16]升序排序为例：

  • 稳定算法（如冒泡排序）：排序后为[16,25（A）,25*（B）]，A 仍在 B 前；
  • 不稳定算法（如直接选择排序）：可能出现[16,25*（B）,25（A）]，A 与 B 次序颠倒。

• 重要性：若数据需保留 “相同关键字的原始次序”（如学生成绩排序，分数相同时保留报名先后），必须选择稳定排序算法。

8.2 插入排序

8.2.1插入排序总述

（1）核心思想​

​ 插入排序的本质是 “逐步构建有序序列”：每一步将一个待排序元素，按其关键字（排序码）大小，插入到已排好序的子序列的合适位置，插入后子序列仍保持有序，重复此过程直到所有元素完成插入。

（2）分类

根据 “查找插入位置的方式” 不同，插入排序分为三类：

• 直接插入排序（顺序查找位置）

• 折半插入排序（折半查找位置）

• 希尔排序（缩小增量分组插入）

8.2.2 直接插入排序

（1）核心思想

​ 当插入第i个元素时，前1~i-1个元素已构成有序序列；通过顺序查找（从后往前逐一比较）找到第i个元素的插入位置，再将插入位置后的元素向后顺移，最终插入第i个元素，保证序列有序。

（2）算法步骤

设待排序元素存于数组R[0..n-1]（讲课中以R0~R5为例，n为元素总数），升序排序：

1. 初始化：将R[0]视为初始有序子序列（单个元素天然有序）；

2. 循环插入：从i=1到i=n-1（共n-1次插入）：

   • 步骤 1：取待插入元素temp = R[i]（临时存储，避免后续移动覆盖）；

   • 步骤 2：顺序查找位置：从j=i-1开始，向前逐一比较R[j]与temp：

     • 若R[j] > temp，则R[j+1] = R[j]（元素向后顺移），j--；

     • 若R[j] ≤ temp，则停止比较，插入位置为j+1；

   • 步骤 3：将temp插入到R[j+1]，完成第i个元素的插入。

（3）举例，n=6，数组R的六个排序码分别为：17，3，25，14，20，9。它的直接插入排序的执行过程下图所示。

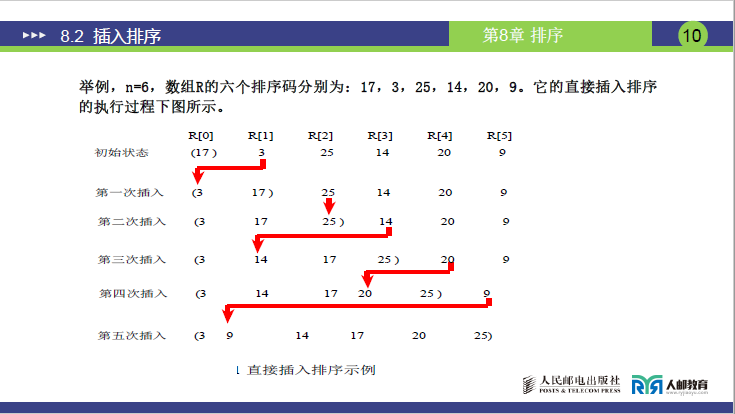
初始化

有序子序列：[17]，待插入元素：3(R1)、25(R2)、14(R3)、20(R4)、9(R5)（共 5 次插入）

第 1 次插入（i=1，temp=3）

• 比较：j=0（R[0]=17），17>3 → R[1]=17（顺移），j=-1；

• 插入位置：j+1=0 → R[0]=3；

• 结果：[3, 17, 25, 14, 20, 9]

第 2 次插入（i=2，temp=25）

• 比较：j=1（R[1]=17），17≤25 → 停止比较；

• 插入位置：j+1=2 → R[2]=25（无需顺移）；

• 结果：[3, 17, 25, 14, 20, 9]

第 3 次插入（i=3，temp=14）

• 比较 1：j=2（R[2]=25），25>14 → R[3]=25（顺移），j=1；

• 比较 2：j=1（R[1]=17），17>14 → R[2]=17（顺移），j=0；

• 比较 3：j=0（R[0]=3），3≤14 → 停止比较；

• 插入位置：j+1=1 → R[1]=14；

• 结果：[3, 14, 17, 25, 20, 9]

第 4 次插入（i=4，temp=20）

• 比较 1：j=3（R[3]=25），25>20 → R[4]=25（顺移），j=2；

• 比较 2：j=2（R[2]=17），17≤20 → 停止比较；

• 插入位置：j+1=3 → R[3]=20；

• 结果：[3, 14, 17, 20, 25, 9]

第 5 次插入（i=5，temp=9）

• 比较 1：j=4（R[4]=25），25>9 → R[5]=25（顺移），j=3；

• 比较 2：j=3（R[3]=20），20>9 → R[4]=20（顺移），j=2；

• 比较 3：j=2（R[2]=17），17>9 → R[3]=17（顺移），j=1；

• 比较 4：j=1（R[1]=14），14>9 → R[2]=14（顺移），j=0；

• 比较 5：j=0（R[0]=3），3≤9 → 停止比较；

• 插入位置：j+1=1 → R[1]=9；

• 最终结果：[3, 9, 14, 17, 20, 25]

（4）性能分析​

指标	说明
时间复杂度	最坏情况：O(n²)（逆序序列，比较n(n-1)/2次，移动(n²+4n-4)/2次）；> 最好情况：O(n)（有序序列，比较n-1次，移动 0 次）；：O(n²)
空间复杂度	O(1)（仅需 1 个临时变量temp存储待插入元素）
稳定性	稳定（若两元素关键字相等，插入时不改变其相对位置，如[2, 1, 1]排序后仍为[1, 1, 2]）

（5）扩展：适用场景

• 适合小规模数据（n≤100）：O(n²)在小规模下效率可接受；

• 适合接近有序的数据：此时接近最好情况，效率远超冒泡、选择排序；

• 实际应用：作为更复杂排序（如希尔排序）的子步骤。

8.2.3 折半插入排序

（1）核心思想

​ 在直接插入排序基础上优化 “查找插入位置” 的方式：利用折半查找（二分查找）替代顺序查找 —— 因前1~i-1个元素已有序，可通过折半快速定位插入位置，减少比较次数；元素移动次数与直接插入排序一致。

（2）算法步骤

设数组R[1..n]，升序排序：

1. 初始化：R[1]为初始有序子序列；

2. 循环插入（i=2到i=n）：

   • 步骤 1：temp = R[i]，定义折半指针low=1（有序子序列左边界）、high=i-1（右边界）；

   • 步骤 2：折半查找位置：

     • 若low ≤ high：

       • 计算mid = (low + high) // 2（中间位置，向下取整）；

       • 若R[mid] > temp：插入位置在左半区，high = mid - 1；

       • 若R[mid] ≤ temp：插入位置在右半区，low = mid + 1；

     • 循环结束后，插入位置为low（因low > high时，low即为待插入索引）；

   • 步骤 3：将R[low..i-1]元素向后顺移 1 位，R[low] = temp。

（3）详细示例（讲课数据：R = [21, 25, 49, 25, 16, 8]，n=6）

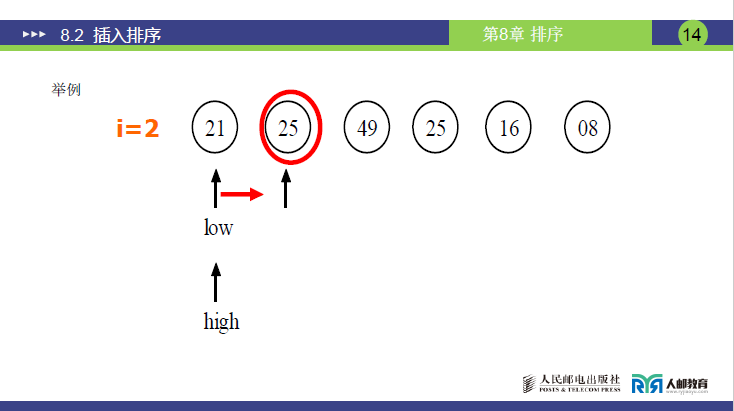
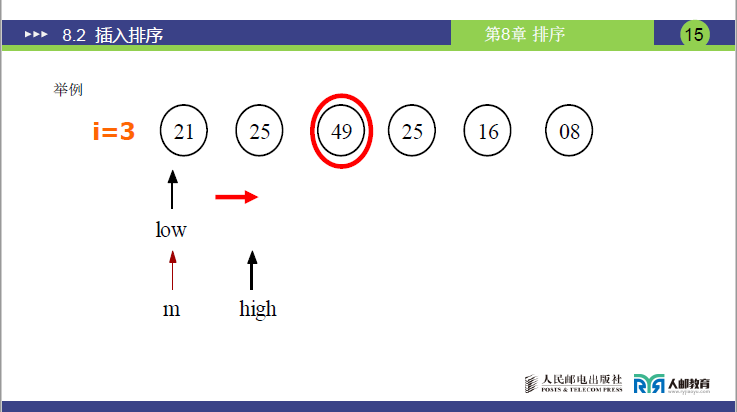
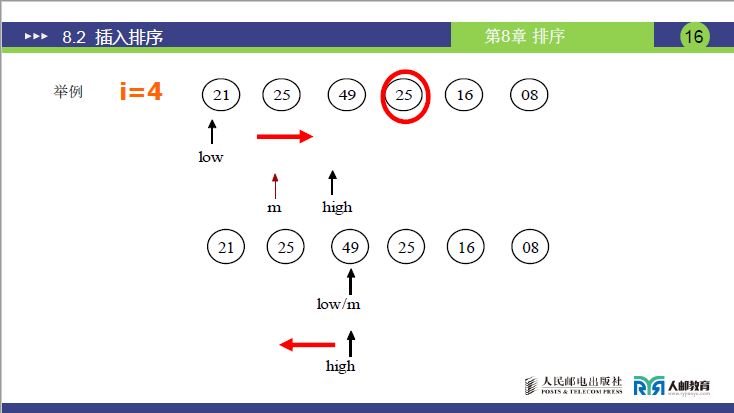
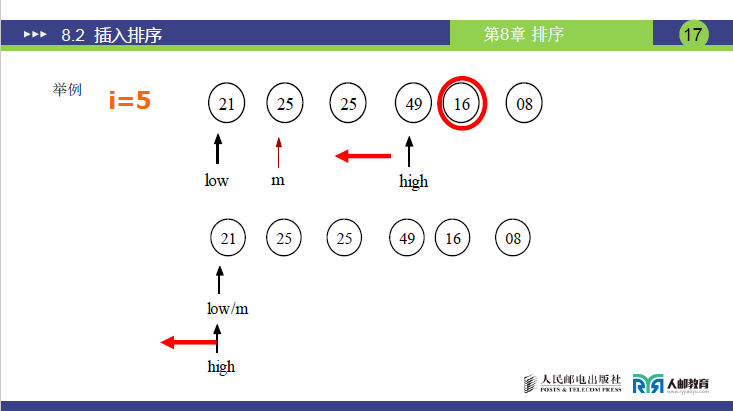
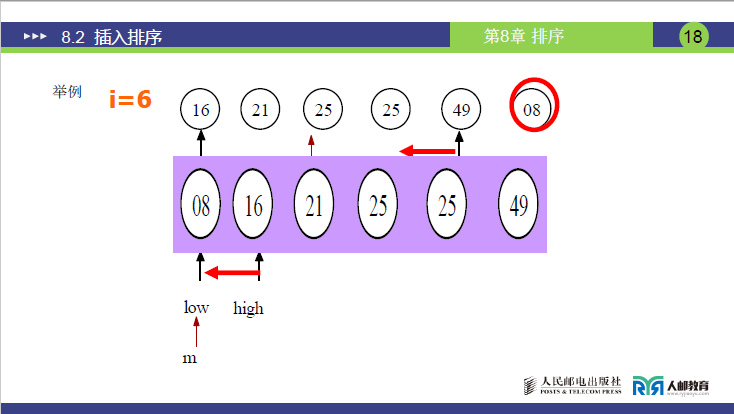
初始化

有序子序列：[21]（R[1]=21），待插入元素：25(R[2])、49(R[3])、25(R[4])、16(R[5])、8(R[6])（注：R[4]=25与R[2]=25关键字相同，用于验证稳定性）

第 1 次插入（i=2，temp=25）

• low=1，high=1（有序子序列仅R[1]=21）；

• 计算mid=(1+1)//2=1：R[1]=21 ≤ 25 → 插入位置在右半区，low=1+1=2；

• 循环结束（low=2 > high=1），插入位置为low=2；

• 无需顺移（low=i=2），直接将temp=25插入R[2]；

• 结果：[21, 25, 49, 25, 16, 8]（R[1]~R[6]，下同）

第 2 次插入（i=3，temp=49）

• low=1，high=2（有序子序列为[21,25]）；

• 第 1 轮折半：mid=(1+2)//2=1 → R[1]=21 ≤ 49 → low=1+1=2；

• 第 2 轮折半：low=2 ≤ high=2，mid=(2+2)//2=2 → R[2]=25 ≤ 49 → low=2+1=3；

• 循环结束（low=3 > high=2），插入位置为low=3；

• 无需顺移（low=i=3），将temp=49插入R[3]；

• 结果：[21, 25, 49, 25, 16, 8]

第 3 次插入（i=4，temp=25）

• low=1，high=3（有序子序列为[21,25,49]）；

• 第 1 轮折半：mid=(1+3)//2=2 → R[2]=25 ≤ 25（关键字相等，取右半区）→ low=2+1=3；

• 第 2 轮折半：low=3 ≤ high=3，mid=(3+3)//2=3 → R[3]=49 > 25（插入位置在左半区）→ high=3-1=2；

• 循环结束（low=3 > high=2），插入位置为low=3；

• 元素顺移：将R[3..3]（即49）向后顺移 1 位至R[4]（原R[4]=25已暂存为temp，无覆盖问题）；

• 将temp=25插入R[3]；

• 结果：[21, 25, 25, 49, 16, 8]（关键：原R[2]=25仍在R[3]=25之前，保持关键字相同元素的相对位置，验证稳定性）

第 4 次插入（i=5，temp=16）

• low=1，high=4（有序子序列为[21,25,25,49]）；

• 第 1 轮折半：mid=(1+4)//2=2 → R[2]=25 > 16 → high=2-1=1；

• 第 2 轮折半：low=1 ≤ high=1，mid=(1+1)//2=1 → R[1]=21 > 16 → high=1-1=0；

• 循环结束（low=1 > high=0），插入位置为low=1；

• 元素顺移：将R[1..4]（21,25,25,49）依次向后顺移 1 位至R[2]~R[5]；

• 将temp=16插入R[1]；

• 结果：[16, 21, 25, 25, 49, 8]

第 5 次插入（i=6，temp=8）

• low=1，high=5（有序子序列为[16,21,25,25,49]）；

• 第 1 轮折半：mid=(1+5)//2=3 → R[3]=25 > 8 → high=3-1=2；

• 第 2 轮折半：low=1 ≤ high=2，mid=(1+2)//2=1 → R[1]=16 > 8 → high=1-1=0；

• 循环结束（low=1 > high=0），插入位置为low=1；

• 元素顺移：将R[1..5]（16,21,25,25,49）依次向后顺移 1 位至R[2]~R[6]；

• 将temp=8插入R[1]；

• 最终结果：[8, 16, 21, 25, 25, 49]（两个25仍保持原相对位置，证明折半插入排序稳定）

（4）性能分析

指标	说明
时间复杂度	仍为O(n²)（元素移动次数与直接插入一致，仅比较次数减少：从O(n)降至O(logn)，但移动次数仍占主导）
空间复杂度	O(1)（同直接插入，仅需临时变量temp）
稳定性	稳定（如示例中两个25，折半查找时因R[mid] ≤ temp取右半区，最终保持原相对位置，未发生顺序颠倒）

（5）扩展：与直接插入的对比

• 优势：减少比较次数，尤其适合数据量稍大的有序 / 接近有序数据（如n=1000时，折半比较仅需 10 次，顺序需约 500 次）；
• 劣势：仍需移动元素，未解决O(n²)的根本问题；
• 适用场景：比直接插入更适合 “中等规模、有序度高” 的数据。

8.2.4 希尔排序（缩小增量排序）

（1）核心思想

​ 突破O(n²)的关键：将整个序列按增量d 分组，每组内用直接插入排序；逐步缩小增量d（如d=3→d=2→d=1），重复分组与排序；当d=1时，整个序列已接近有序，仅需一次直接插入排序即可完成。

​ 设待排序的数据对象有n个，首先取一个整数d < n作为间隔，将全部对象分为d个子序列，所有距离为d的对象放在同一个序列中，在每一个子序列中分别施行直接插入排序，然后缩小间隔d，如取d=d/2，重复上述的子序列划分和排序工作，直到最后取d为1为止。

（2）关键：增量d的取值

①经典取值方案

• 希尔原方案：d₁ = n//2，dₖ₊₁ = dₖ//2，直到d=1（如n=6时，d=3→1）；

• 优化方案：d₁ = n，dₖ₊₁ = dₖ//3 +1（避免d为偶数时分组重复，如n=10时，d=10→4→2→1）；

• 原则：d需逐步缩小至 1，且相邻增量最好互质（减少重复排序，提升效率）。

（3）算法步骤

设数组R[1..n]，升序排序：

1. 确定增量序列（如d₁, d₂, ..., dₖ=1）；

2. 对每个增量d：

   • 将序列分为d组：第1组R[1], R[1+d], R[1+2d]...，第2组R[2], R[2+d], R[2+2d]...，…，第d组R[d], R[d+d], R[d+2d]...；

   • 每组内独立执行直接插入排序；

3. 当d=1时，排序完成。

（4）详细示例（讲课数据：R = [21, 25, 49, 25, 16, 8]，n=6，数组序号 1~6，增量d=3→2→1）

初始序列：[21, 25, 49, 25, 16, 8]（R[1]~R[6]，R[4]=25与R[2]=25为相同关键字，用于验证稳定性）

第 1 趟：增量d=3（分 3 组，每组间隔 3）

• 分组：

• 组 1：R[1], R[1+3]=R[4] → [21, 25]（直接插入排序后不变）；

• 组 2：R[2], R[2+3]=R[5] → [25, 16]（排序后→[16, 25]）；

• 组 3：R[3], R[3+3]=R[6] → [49, 8]（排序后→[8, 49]）；

• 替换回原数组（R[1]~R[6]）：[21, 16, 8, 25, 25, 49]

第 2 趟：增量d=2（分 2 组，每组间隔 2）

• 分组：

• 组 1：R[1], R[1+2]=R[3], R[1+4]=R[5] → [21, 8, 25]（排序后→[8, 21, 25]）；

• 组 2：R[2], R[2+2]=R[4], R[2+4]=R[6] → [16, 25, 49]（排序后不变）；

• 替换回原数组（R[1]~R[6]）：[8, 16, 21, 25, 25, 49]（此趟后序列已有序，第 3 趟无需额外操作）

第 3 趟：增量d=1（整个序列为 1 组，直接插入排序）

• 序列已接近有序：[8, 16, 21, 25, 25, 49]；

• 无需额外比较与移动，最终结果保持不变：[8, 16, 21, 25, 25, 49]

（5）性能分析

注：Shell 排序中 d 的取法

• Shell最初的方案是：

  • d = n/2，d = d/2，直到d = 1。

• Knuth的方案是：

  • d = d/3+1

• 其它方案有，都取奇数为好；或d互质为好等等。

• 对Shell排序的时间复杂度的分析很困难，在特定情况下可以准确地估算关键码的比较和数据对象移动次数，但是考虑到与增量之间的依赖关系，并要给出完整的数学分析，目前还做不到。

• Shell排序中所需的比较和移动次数约为n^1.3。

• Knuth的统计结论是数据对象平均比较次数和移动次数是在n^1.25 与1.6n^1.25之间。

• 故：Shell排序的时间复杂度为O(n^1.3)。

  • Shell 排序的空间复杂度为O(0)。
  • Shell 排序是一种不稳定的排序方法。

指标	说明
时间复杂度	无精确公式，与增量序列相关：希尔原方案：O(n²)；优化增量（如dₖ//3+1）：O(n^1.3)（平均情况）；：O(n(log₂n)²)
空间复杂度	O(1)（仅需临时变量，无额外空间）
稳定性	不稳定（分组排序时，相同关键字元素可能被分到不同组，导致相对位置改变；本例因数据特性未体现，若初始序列为[25, 21, 49, 25, 16, 8]，分组后可能出现顺序颠倒）

（6）扩展：适用场景

• 适合中大规模数据（n=1000~100000）：O(n^1.3)远优于直接插入的O(n²)；

• 工业应用：作为快排、归并排序的补充，在某些硬件环境（如缓存友好）下性能优异；

• 注意：希尔排序不适合要求 “稳定排序” 的场景（如电商订单按 “价格 + 时间” 排序，时间不能乱序）。

8.2.5 插入排序三种方法对比总结

对比维度	直接插入排序	折半插入排序	希尔排序
核心差异	顺序查找位置	折半查找位置	缩小增量分组插入
时间复杂度	最坏O(n²)，最好O(n)	最坏O(n²)，最好O(n)	平均O(n^1.3)
空间复杂度	O(1)	O(1)	O(1)
稳定性	稳定	稳定	不稳定
比较次数	多（O(n)/ 次插入）	少（O(logn)/ 次）	少（分组减少比较）
移动次数	多（O(n)/ 次插入）	多（同直接插入）	少（分组后移动距离短）
适用场景	小规模、接近有序数据	中等规模、有序数据	中大规模数据

8.3 交换排序

8.3.1交换排序定义

交换排序是基于 “两两比较关键字，交换不满足顺序要求的记录对” 的排序思想，核心是通过反复交换逆序记录，使整个序列逐步有序。

• 核心原理：在待排序记录序列中，两两比较相邻（或指定）记录的关键字，若存在逆序（如要求升序时 “前大后小”），则交换这两个记录，直到所有记录都满足顺序要求。
• 常见方法：冒泡排序、快速排序（二者是考试重点，尤其快速排序需与堆排序共同掌握）。
• 关键区分：需与 “简单选择排序” 区分 —— 冒泡排序是相邻两两比较，而简单选择排序是 “第 i 个记录与后续所有记录比较”，二者比较逻辑完全不同。

8.3.2冒泡排序（Bubble Sort）

（1）基本思想

通过相邻记录的两两比较与逆序交换，使关键字小的记录像 “气泡” 一样向上浮动，或关键字大的记录像 “石头” 一样向下沉落，最终实现有序。

• 两种操作方向（讲课核心补充）：
  • 「冒泡方向」：自后向前比较（j 从 n-1 递减到 1），每次找到当前未排序部分的最小关键字，将其 “冒” 到未排序部分的最前端。
  • 「石沉大海方向」：自前向后比较（i 从 1 递增到 n-1），每次找到当前未排序部分的最大关键字，将其 “沉” 到未排序部分的最后端。
• 优化点：无需固定执行 n-1 趟 —— 若某一趟比较中未发生任何交换，说明序列已完全有序，可直接终止排序（提升效率）。

（2）算法步骤（以升序为例，分两种方向）

方向 1：石沉大海（自前向后，找最大沉底）

1. 初始序列为r[1..n]（n 为记录个数），未排序区间初始为[1..n]。
2. 第 1 趟：在[1..n]内，从i=1开始，两两比较r[i]与r[i+1]：
   • 若r[i].key > r[i+1].key，交换二者；
   • 遍历结束后，最大关键字沉到r[n]，未排序区间缩小为[1..n-1]。
3. 第 k 趟：在[1..n-k+1]内重复步骤 2，将当前未排序区间的最大关键字沉到r[n-k+1]，未排序区间缩小为[1..n-k]。
4. 重复上述过程，直到某一趟无交换或完成 n-1 趟（实际通常提前终止）。

方向 2：冒泡（自后向前，找最小冒顶）

1. 未排序区间初始为[1..n]。
2. 第 1 趟：在[1..n]内，从j=n开始，两两比较r[j]与r[j-1]：
   • 若r[j].key < r[j-1].key，交换二者；
   • 遍历结束后，最小关键字冒到r[1]，未排序区间缩小为[2..n]。
3. 第 k 趟：在[k..n]内重复步骤 2，将当前未排序区间的最小关键字冒到r[k]，未排序区间缩小为[k+1..n]。
4. 直到某一趟无交换或完成 n-1 趟。

（3）详细举例（讲课重点拆解）

举例，n=6，数组R的六个排序码分别为：17，3，25，14，20，9。
下图给出冒泡排序算法的执行过程。

例 1：n=6，初始序列[17, 3, 25, 14, 20, 9]（冒泡方向：自后向前找最小冒顶）

• 初始化：r[0]（哨兵位）空，r[1..6] = [17, 3, 25, 14, 20, 9]（未排序区间[1..6]）。

• 第 1 趟（目标：冒最小关键字 “3” 到r[1]）：

  1. j=6：r[6]=9与r[5]=20比较（9<20）→ 交换，序列变为[17, 3, 25, 14, 9, 20]；
  2. j=5：r[5]=9与r[4]=14比较（9<14）→ 交换，序列变为[17, 3, 25, 9, 14, 20]；
  3. j=4：r[4]=9与r[3]=25比较（9<25）→ 交换，序列变为[17, 3, 9, 25, 14, 20]；
  4. j=3：r[3]=9与r[2]=3比较（9>3）→ 不交换；
  5. j=2：r[2]=3与r[1]=17比较（3<17）→ 交换，序列变为[3, 17, 9, 25, 14, 20]；
  • 结果：最小关键字 “3” 冒到r[1]，未排序区间缩小为[2..6]。

• 第 2 趟（目标：冒未排序区间[2..6]的最小关键字 “9” 到r[2]）：

  1. j=6：20与14（20>14）→ 交换，序列[3,17,9,25,20,14]；
  2. j=5：20与25（20<25）→ 交换，序列[3,17,9,20,25,14]；
  3. j=4：20与9（20>9）→ 不交换；
  4. j=3：9与17（9<17）→ 交换，序列[3,9,17,20,25,14]；
  • 结果：“9” 冒到r[2]，未排序区间[3..6]。

• 第 3~5 趟：依次冒 “14”“17”“20” 到对应位置，第 5 趟后序列为[3,9,14,17,20,25]，第 6 趟无交换→排序终止。

例 2：n=8，初始序列[38, 49, 65, 97, 76, 13, 27, 30]（石沉大海方向：自前向后找最大沉底）

• 初始化：r[1..8] = [38,49,65,97,76,13,27,30]（未排序区间[1..8]）。

• 第 1 趟（目标：沉最大关键字 “97” 到r[8]）：

  1. i=1：38<49→不交换；i=2：49<65→不交换；i=3：65<97→不交换；
  2. i=4：97>76→交换，序列[38,49,65,76,97,13,27,30]；
  3. i=5：97>13→交换，序列[38,49,65,76,13,97,27,30]；
  4. i=6：97>27→交换，序列[38,49,65,76,13,27,97,30]；
  5. i=7：97>30→交换，序列[38,49,65,76,13,27,30,97]；
  • 结果：“97” 沉到r[8]，未排序区间[1..7]。

• 第 2~5 趟：第 2 趟沉 “76” 到r[7]，第 3 趟沉 “65” 到r[6]，第 4 趟沉 “49” 到r[5]，第 5 趟无交换→序列有序[13,27,30,38,49,65,76,97]。

（4）性能分析

指标	具体说明
时间复杂度	最坏情况（逆序）：$比较次数 = \sum_{i=1}^{n-1} (n-i) = \frac{1}{2} (n^2 - n) \(，\)移动次数 = \sum_{i=1}^{n} (n-i) = \frac{3}{2} (n^2 - n)$→时间复杂度O(n²)；最好情况（有序）：比较次数n-1，移动次数0→时间复杂度O(n)；平均情况：O(n²)。
空间复杂度	仅需 1 个临时变量存储交换数据→O(1)（原地排序）。
稳定性	稳定排序：若存在相同关键字（如25和25*），排序后二者相对位置不变（相邻交换不破坏相同元素顺序）。
适用场景	数据量小、接近有序的场景（优化后可提前终止，效率较高）。

8.3.3快速排序（Quick Sort）

快速排序是 “分治法” 的典型应用，是平均效率最高的内部排序算法之一，但需注意 “数据有序程度对效率影响极大”。

（1）基本思想

​ 是取待排序的结点序列中某个结点的值作为控制值，采用某种方法把这个结点放到适当的位置，使得这个位置的左边的所有结点的值都小于等于这个控制值，而这个位置的右边的所有结点的值都大于等于这个控制值。然后分别对这两个子序列重复实施上述方法。

1. 选控制值（枢轴 / Pivot）：从待排序序列中选一个记录作为 “控制值”（讲课中称为 “旗杆”，通常选第一个元素）；
2. 分区（Partition）：将序列分为两部分 —— 左部分所有记录的关键字小于控制值，右部分所有记录的关键字大于控制值，控制值放到最终位置（“旗杆立住”）；
3. 递归排序：对左、右两个子序列重复步骤 1~2，直到子序列长度为 1（天然有序）。

• 核心特点（讲课重点）：
  • 数据越乱，效率越高（控制值能均匀分区）；
  • 数据基本有序时，效率最差（控制值偏向一端，分区失衡）。

（2）算法步骤（以升序为例，选第一个元素为控制值）

1. 初始化：设待排序序列为r[low..high]，初始化指针i=low（左指针，指向序列起点）、j=high（右指针，指向序列终点），控制值key = r[low].key（存第一个元素的关键字）。
2. 右指针左移（找小于 key 的记录）：j从high开始向左递减，直到找到r[j].key < key，将r[j]赋值给r[i]（此时j位置为空）；
3. 左指针右移（找大于 key 的记录）：i从low开始向右递增，直到找到r[i].key > key，将r[i]赋值给r[j]（此时i位置为空）；
4. 重复分区：循环执行步骤 2~3，直到i = j（此时i/j为控制值的最终位置），将key赋值给r[i]；
5. 递归处理子序列：对左子序列r[low..i-1]和右子序列r[i+1..high]重复步骤 1~4，直到所有子序列有序。

• 关键细节（讲课补充）：
  • 先动j再动i：因为控制值取自low（左起点），需先从右侧找 “小值” 填充左侧空位，避免控制值位置错乱；
  • 相等关键字不交换：若r[j].key == key或r[i].key == key，继续移动指针，保证分区逻辑一致。

（3）详细举例（讲课重点拆解）

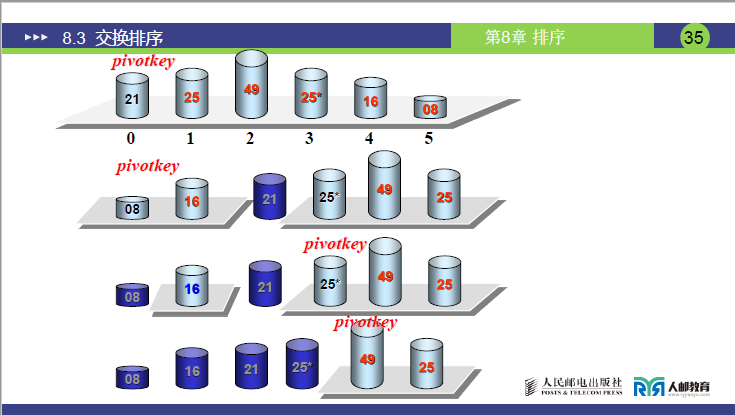
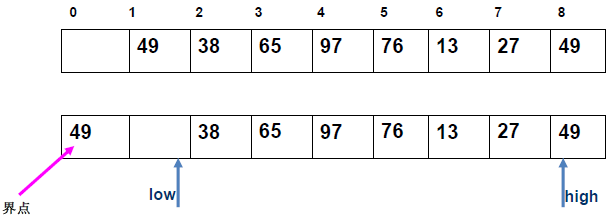
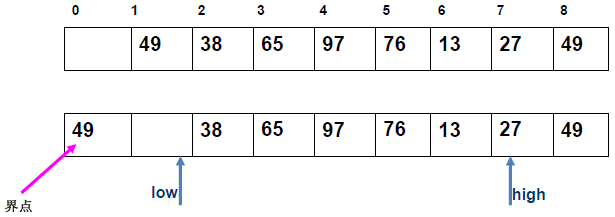
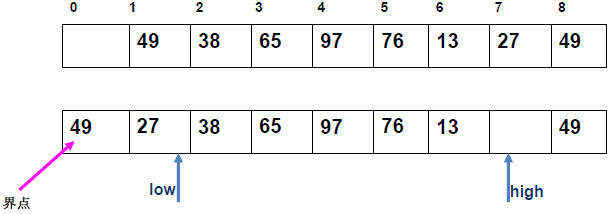
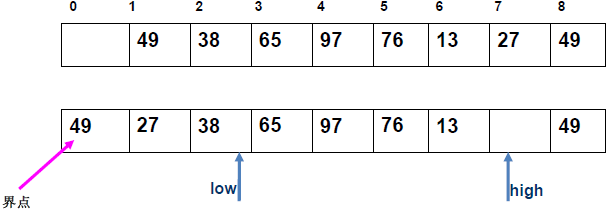
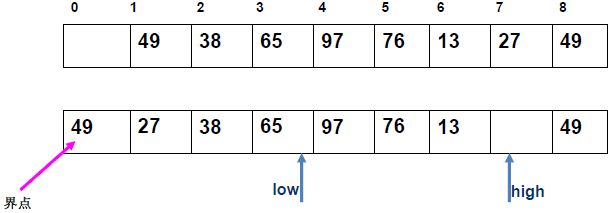
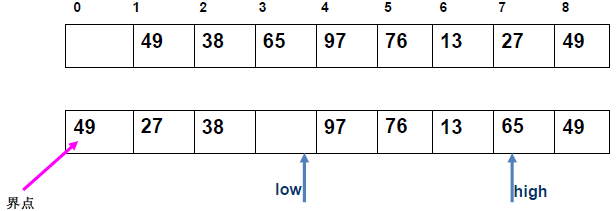
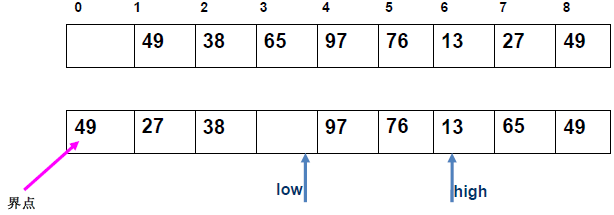
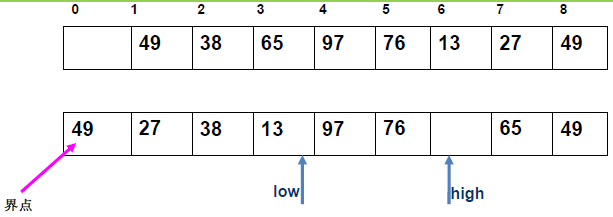
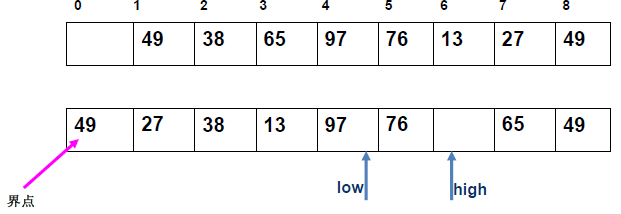
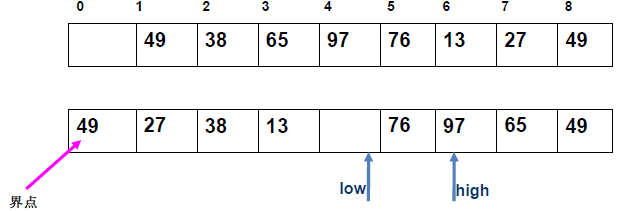
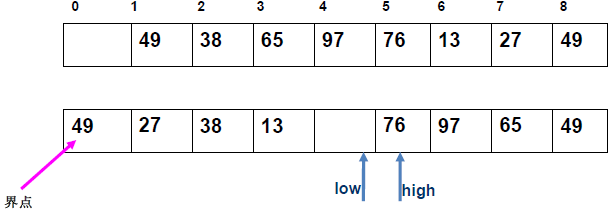
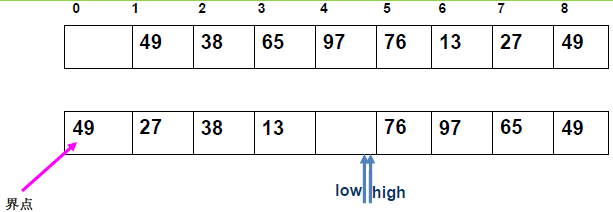
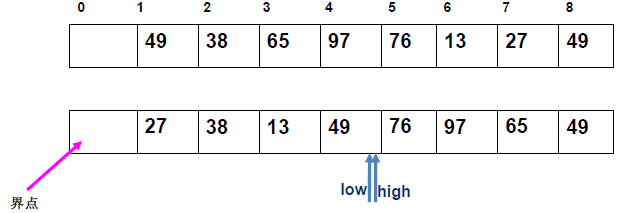
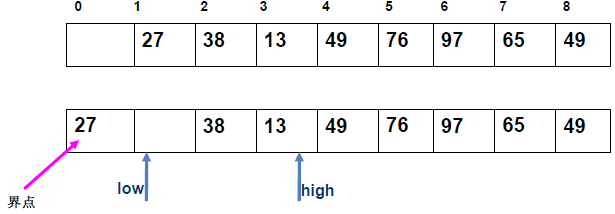
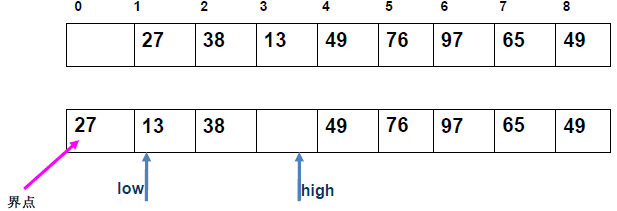
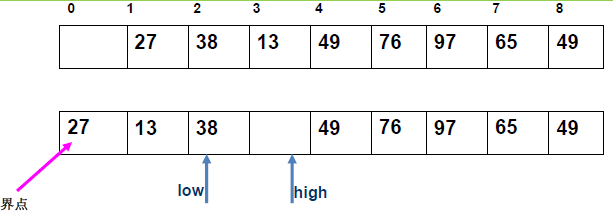
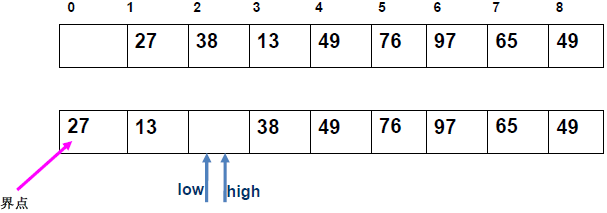
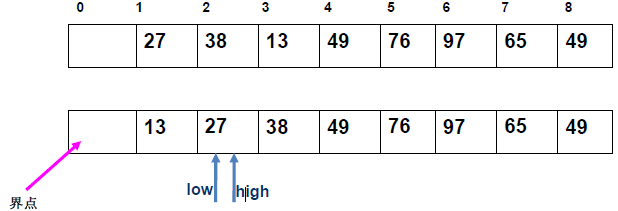
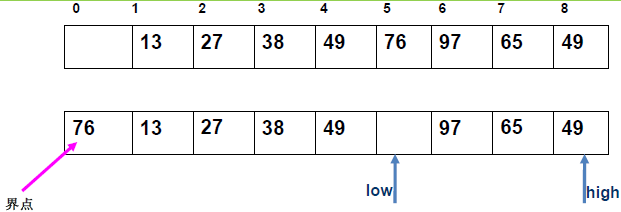
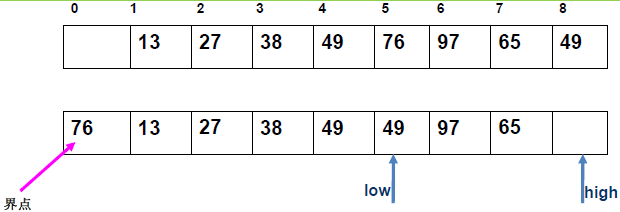
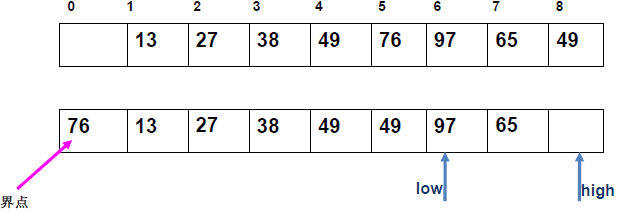
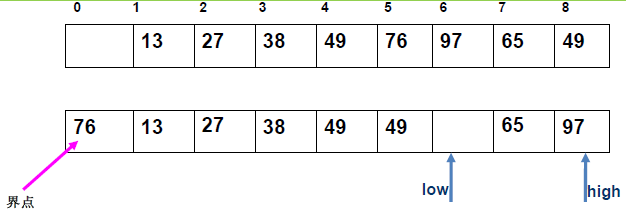
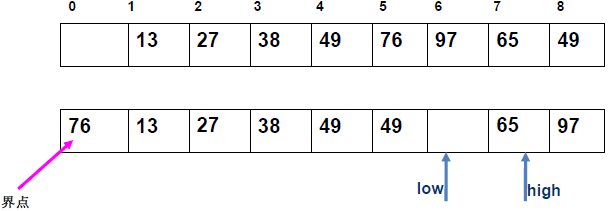
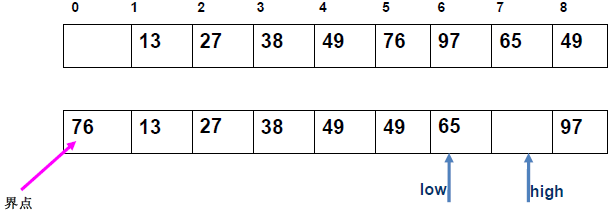
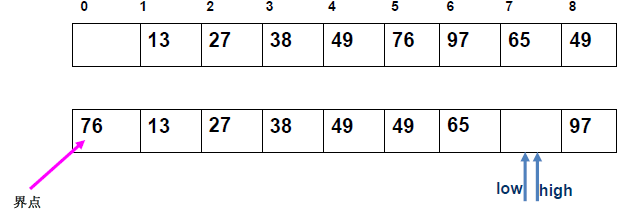
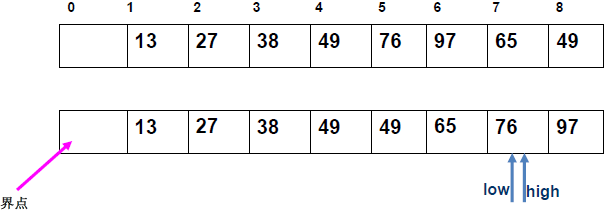
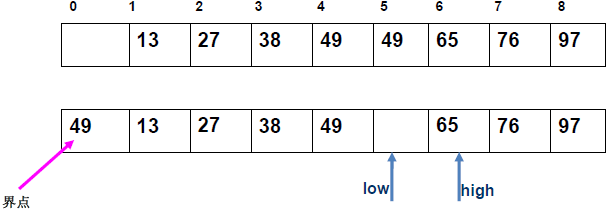
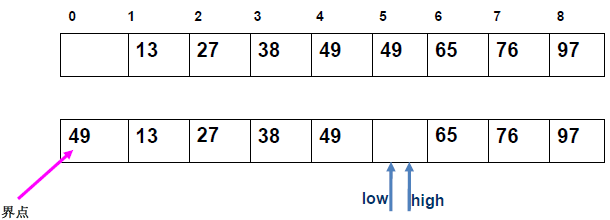
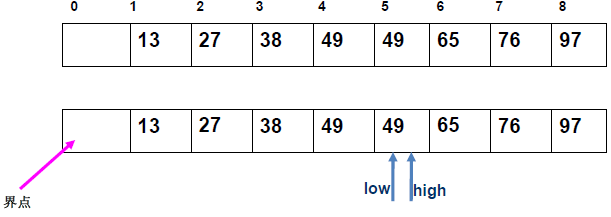
例 1：n=6，初始序列[21, 25, 49, 25*, 16, 08]（low=1，high=6，key=21）

• 第 1 趟分区（目标：确定 21 的最终位置）：

  1. 初始化：i=1，j=6，key=21，序列[21,25,49,25*,16,08]；
  2. j左移：找r[j].key < 21→j=6（08<21），将r[6]赋值给r[1]→序列[08,25,49,25*,16,08]（j=6空）；
  3. i右移：找r[i].key > 21→i=2（25>21），将r[2]赋值给r[6]→序列[08,25,49,25*,16,25]（i=2空）；
  4. j左移：找r[j].key <21→j=5（16<21），将r[5]赋值给r[2]→序列[08,16,49,25*,16,25]（j=5空）；
  5. i右移：找r[i].key >21→i=3（49>21），将r[3]赋值给r[5]→序列[08,16,49,25*,49,25]（i=3空）；
  6. j左移：j=4（25*>21）→继续左移到j=3，此时i=j=3；
  7. 控制值归位：将key=21赋值给r[3]→序列[08,16,21,25*,49,25]；
  • 结果：控制值 21 的最终位置是i=3，左子序列[08,16]（low=1,high=2），右子序列[25*,49,25]（low=4,high=6）。

• 递归排序左子序列[08,16]：

  • key=08，i=1，j=2：j左移找 < 08（无），i=j=1，08 归位→左子序列有序；
  • 右子序列[16]天然有序。

• 递归排序右子序列[25\*,49,25]：

  • key=25，i=4，j=6：j找 < 25（j=6，25<25）→赋值给r[4]，i找 > 25（i=5，49>25*）→赋值给r[6]，j左移到i=j=5，25 * 归位→右子序列变为[25,25*,49]，最终有序。

• 最终序列：[08,16,21,25,25*,49]。

例 2：n=8，初始序列[46,55,13,42,94,05,17,70]（仅需第一次划分）

• 初始化：low=1，high=8，key=46，i=1，j=8，序列[46,55,13,42,94,05,17,70]；

• 第一次划分步骤：

  1. j左移：找r[j].key <46→j=7（17<46），将r[7]赋值给r[1]→序列[17,55,13,42,94,05,17,70]（j=7空）；
  2. i右移：找r[i].key >46→i=2（55>46），将r[2]赋值给r[7]→序列[17,55,13,42,94,05,55,70]（i=2空）；
  3. j左移：找r[j].key <46→j=6（05<46），将r[6]赋值给r[2]→序列[17,05,13,42,94,05,55,70]（j=6空）；
  4. i右移：找r[i].key >46→i=5（94>46），将r[5]赋值给r[6]→序列[17,05,13,42,94,94,55,70]（i=5空）；
  5. j左移：找r[j].key <46→j=4（42<46），将r[4]赋值给r[5]→序列[17,05,13,42,42,94,55,70]（j=4空）；
  6. i右移：i=5（94>46）→继续右移到i=4，此时i=j=4；
  7. 控制值归位：将key=46赋值给r[4]→第一次划分结果：[17,05,13,46,42,94,55,70]；
  • 分区结果：左子序列[17,05,13]（low=1,high=3），右子序列[42,94,55,70]（low=5,high=8）。

（4）性能分析

指标	具体说明
时间复杂度	最好情况（控制值每次分中间，均匀分区）：O(nlog₂n)（递归深度log₂n，每趟比较n次）； 最坏情况（数据基本有序，控制值分在一端）：O(n²)（递归深度n，每趟比较n次）； 平均情况：O(nlog₂n)（实际应用中效率最高的内部排序）。
空间复杂度	递归栈空间：最好情况O(log₂n)（递归深度log₂n），最坏情况O(n)（递归深度n）→非原地排序。
稳定性	不稳定排序：若相同关键字在控制值两侧，可能因交换改变相对位置（如[25*,25]可能变为[25,25*]）。
适用场景	数据量较大、数据杂乱无章的场景（避免基本有序数据，否则效率骤降）。

8.3.4冒泡排序与快速排序对比

对比维度	冒泡排序	快速排序
基本思想	相邻两两交换，逐步浮动 / 沉落	分治法，选控制值分区后递归排序
比较方式	仅相邻记录比较	左右指针双向比较
时间复杂度	最坏 / 平均O(n²)，最好O(n)	最坏O(n²)，平均 / 最好O(nlog₂n)
空间复杂度	O(1)（原地）	O(log₂n)~O(n)（递归栈）
稳定性	稳定	不稳定
适用数据规模	小规模数据	大规模数据
数据有序影响	有序时效率最高（提前终止）	有序时效率最低（分区失衡）

8.4 选择排序

8.4.1选择排序概述

（1）定义

选择排序(Select Sort)的基本原理，是将待排序的记录分为已排序(初始为空)和未排序两组，依次将未排序的记录中关键字码最小的记录插入已排序的组中。

常见的选择排序方法有：简单选择排序、树型(锦标赛)排序、堆排序等。

8.4.2简单选择排序

（1）基本原理

①基本思想

在每一趟带排序的记录中选出关键字最小的记录，按照顺序排放在已经排好序的记录序列的最后，直到序列全部有序。

②算法步骤

从长度为 n 的待排序序列中，依次完成以下操作：

1. 第 i 趟排序时，在待排序区间 [i,n−1] 中找到关键字最小的记录，记录其下标 minIndex。
2. 将下标为 minIndex的记录与下标为 i 的记录交换位置。
3. 重复上述步骤，直到 i 遍历至 n−2（最后一个元素无需排序）。

与冒泡排序的核心区别：

• 冒泡排序：通过相邻元素两两交换逐步将最大 / 最小元素 “浮” 到序列末端，每趟交换次数多。
• 简单选择排序：每趟只进行一次交换（找到最小元素后一次性交换到目标位置），减少交换操作次数。

（2）实例演示

以老师课堂示例（8 个无序数，目标升序排序）为例，假设初始序列为 [8,3,2,4,1,5,7,6]，排序过程如下：

• 第 1 趟：待排序区间 [0,7]，找到最小元素 1（下标 4），与下标 0 的元素 8 交换 → 序列变为 [1,3,2,4,8,5,7,6]
• 第 2 趟：待排序区间 [1,7]，找到最小元素 2（下标 2），与下标 1 的元素 3 交换 → 序列变为 [1,2,3,4,8,5,7,6]
• 第 3 趟：待排序区间 [2,7]，最小元素为 3（自身），无需交换 → 序列保持不变
• 后续趟数：依次在剩余区间找最小元素并交换，最终得到有序序列 [1,2,3,4,5,6,7,8]

（3）性能分析

• 时间复杂度：O(n²)
  • 无论序列是否有序，都需要进行 n(n−1)/2 次比较操作；交换操作最多 n−1 次。
• 空间复杂度：O(1)
  • 仅需常数级临时变量存储最小元素下标，属于原地排序。
• 稳定性：不稳定排序
  • 例如序列 [2,2,1]，第一趟交换第一个 2 和 1 后，两个 2 的相对顺序发生变化。

8.4.3树形选择排序（锦标赛排序）

（1）基本原理

采用锦标赛思想，以完全二叉树为载体实现排序，核心步骤如下：

1. 构建完全二叉树：将待排序的 n 个元素放在二叉树的叶子节点。
2. 两两比较选优：从叶子节点开始，两两比较元素大小，将较小值（升序排序）向上传递至父节点，最终根节点为整个序列的最小值。
3. 输出并更新树：输出根节点的最小值，将其对应的叶子节点值置为 ∞（表示已选出），重新从该叶子节点向上比较更新二叉树，得到新的根节点（剩余元素的最小值）。
4. 重复操作：直到所有叶子节点的值均为 ∞，输出的序列即为有序序列。

（2）实例演示

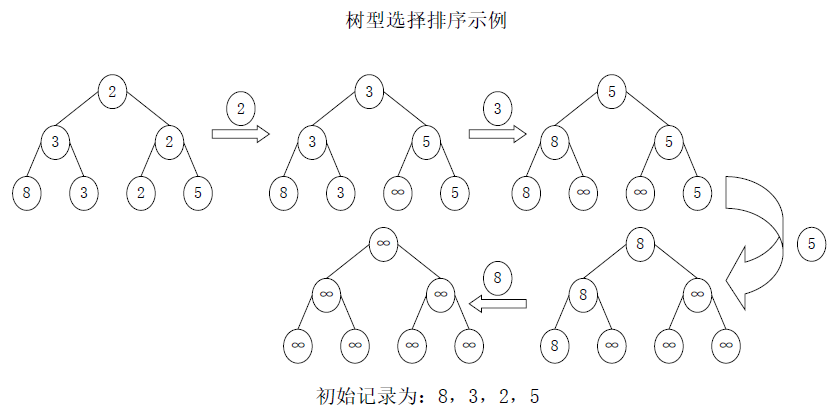
以老师课堂示例（4 个无序数，假设为 [5,3,8,2]）为例，排序过程如下：

• 叶子节点：5,3,8,2
• 第一轮比较：5↔3 选 3；8↔2 选 2 → 父节点为 3,2；根节点选 2（最小值）
• 输出 2，将对应叶子节点置为 ∞ → 叶子节点变为 5,3,8,∞
• 第二轮比较：8↔∞ 选 8；5↔3 选 3 → 父节点为 3,8；根节点选 3
• 输出 3，对应叶子节点置为 ∞ → 重复操作，最终输出有序序列 [2,3,5,8]

（3）性能分析

• 时间复杂度：O(nlog₂n)
  • 完全二叉树的高度为 ⌈log₂n⌉+1，每次更新树的比较次数不超过树的高度，整体比较次数为 O(nlog₂n)。
• 空间复杂度：O(n)
  • 需要额外存储完全二叉树的非叶子节点，空间开销较大。
• 稳定性：稳定排序
  • 关键字相同的元素在比较过程中相对顺序不会改变。

8.4.4 堆排序（选择排序核心考点）

​ 堆排序是树形选择排序的优化版本，克服了树形选择排序空间开销大的缺点，是高效的原地排序算法。

（1）堆的定义与分类

①定义

堆排序实际上是对树型排序的一个改造，它克服了树型排序所需要的巨大附加空间。
n个元素的序列H＝{k₁，k₂，…，k_n}，对于所有的i＝1，2，…，⌊n/2⌋，当它满足如下关系：
① k_i >= k_2i 且k_i >= k_2i+1或
②k_i <= k_2i 且 k_i <= k_2i+1 (1<=i<= ⌊n/2⌋)
则称该序列H为堆。

②性质

​ 堆是一个完全二叉树，且满足以下性质：对于任意节点 i（对应数组下标），其左孩子为 2i+1，右孩子为 2i+2，双亲节点为 ⌊(i−1)/2⌋。

根据节点值的大小关系，堆分为两类：

堆的类型	核心性质	根节点特征
大根堆（大顶堆）	所有双亲节点的值 大于等于 其孩子节点的值	根节点为序列的最大值
小根堆（小顶堆）	所有双亲节点的值 小于等于 其孩子节点的值	根节点为序列的最小值

注意：堆的定义要求所有有孩子的双亲节点都满足上述性质，而非单个节点。

（2）堆的性质

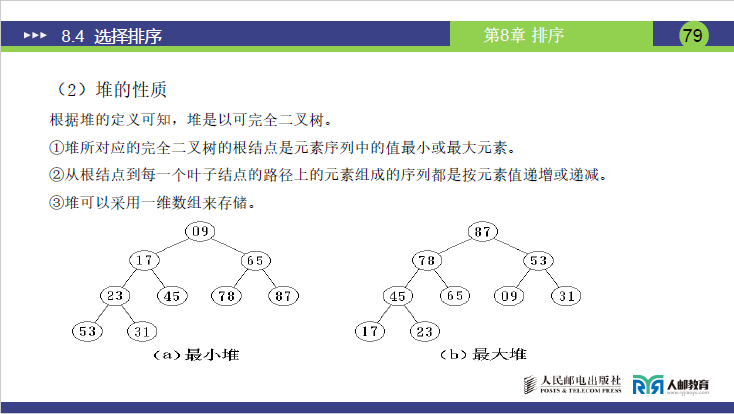
• 堆是一棵完全二叉树（所有层除最后一层外均满，最后一层节点靠左排列）。
• 根节点是序列的极值（最大或最小），即 “堆顶为极值”。
• 从根节点到任意叶子节点的路径上，关键字严格递增（小顶堆）或严格递减（大顶堆）。
• 堆可通过一维数组存储（完全二叉树的天然优势）：若父节点在索引i，则左子节点在2i，右子节点在2i+1（数组从 1 开始索引）。

• 小顶堆（图 (a)）：[9,17,65,23,45,78,87,53,31]，根 9 最小，路径9→17→23→53递增。
• 大顶堆（图 (b)）：[87,78,53,45,65,9,31,17,23]，根 87 最大，路径87→78→45→17递减。

（3）堆排序的核心操作

堆排序的核心是 “建初堆” 和 “筛选法调整堆”，两步循环执行即可完成排序。

①筛选法调整堆

作用：当堆的某一节点值被修改后（如根节点被替换），通过 “向下筛选” 恢复堆的性质。

算法步骤（以大顶堆为例）：

1. 设待调整节点为r[s]，其左子节点为r[2s]，右子节点为r[2s+1]。
2. 找出r[s]、r[2s]、r[2s+1]中的最大关键字，记其位置为max_idx。
3. 若max_idx == s：说明r[s]已是子树的最大值，堆结构正常，无需调整。
4. 若max_idx != s：交换r[s]与r[max_idx]；此时r[max_idx]的位置可能破坏子堆结构，需将s更新为max_idx，重复步骤 2-3，直至s为叶子节点。

②建初堆

作用：将无序序列初始化为堆（大顶堆或小顶堆）。

算法步骤：

1. 将无序序列按完全二叉树结构存入一维数组（索引从 1 开始）。
2. 从最后一个非叶子节点（索引⌊2n⌋）开始，自下向上、自右向左，对每个节点执行 “筛选法调整堆”。
   • 最后一个非叶子节点：⌊2n⌋，因为其右子节点为2*\(\lfloor \frac{n}{2} \rfloor\)+1 ≤n，是最后一个有子节点的父节点。

讲课补充：建初堆的关键是 “从下往上调整”—— 若从上往下调整，下层未调整的大值可能无法上浮到堆顶，导致建堆失败。

（4）堆排序的完整算法步骤

以 “大顶堆实现从小到大排序” 为例（核心：每次取堆顶最大元素，放序列末尾）：

1. 建初堆：将待排序序列初始化为大顶堆（堆顶为最大元素）。
2. 交换堆顶与末尾元素：将堆顶（最大元素）与未排序组的最后一个元素交换，此时最大元素进入 “已排序组”（序列末尾），未排序组长度减 1。
3. 调整堆：交换后堆结构被破坏，对新的堆顶（原末尾元素）执行 “筛选法调整堆”，恢复大顶堆性质。
4. 重复步骤 2-3：共执行n-1次，直至未排序组仅剩 1 个元素，排序结束。

（5）示例 1：建初堆

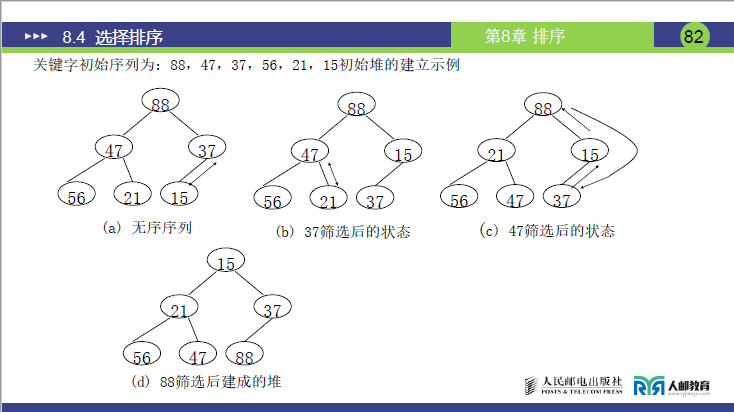
题目：关键字初始序列为[88,47,37,56,21,15]，建立小顶堆（对应课件 P82 图 (a)-(d)）。

详细步骤（自下向上调整，最后一个非叶子节点⌊6/2⌋=3，即节点 37）

1. 初始无序序列（完全二叉树）（课件 P82 图 (a)）：
   • 数组：[88,47,37,56,21,15]（索引 1-6）
   • 结构：根 88，左子 47、右子 37；47 的左子 56、右子 21；37 的左子 15。
2. 调整节点 37（索引 3）（课件 P82 图 (b)）：
   • 节点 37 的子节点：15（索引 6），37>15，交换 37 与 15→数组变为[88,47,15,56,21,37]。
3. 调整节点 47（索引 2）（课件 P82 图 (c)）：
   • 节点 47 的子节点：56（索引 4）、21（索引 5），47>21，交换 47 与 21→数组变为[88,21,15,56,47,37]。
4. 调整节点 88（索引 1）（课件 P82 图 (d)）：
   • 节点 88 的子节点：21（索引 2）、15（索引 3），88>15，交换 88 与 15→数组变为[15,21,88,56,47,37]。
   • 此时节点 88（索引 3）的子节点：37（索引 6），88>37，交换 88 与 37→数组变为[15,21,37,56,47,88]。
   • 节点 88（索引 6）为叶子，调整结束，小顶堆建成。

（6）示例 2：堆排序完整过程

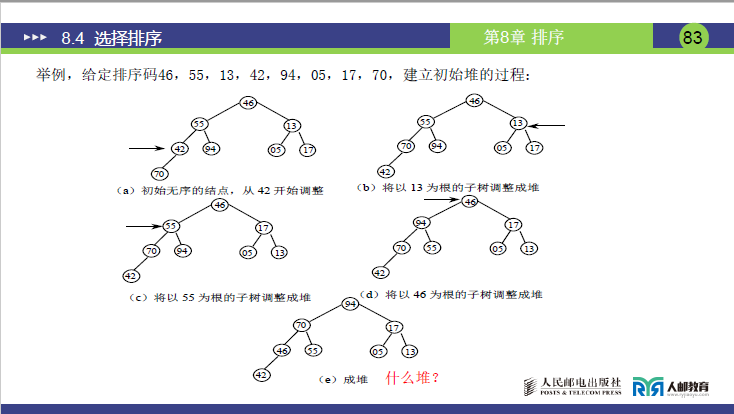
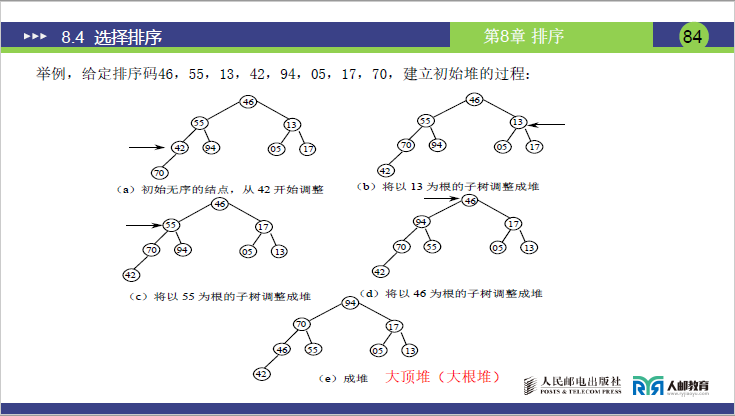
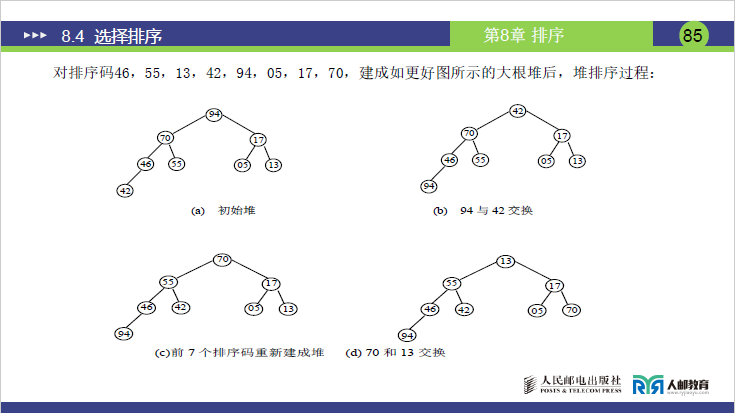
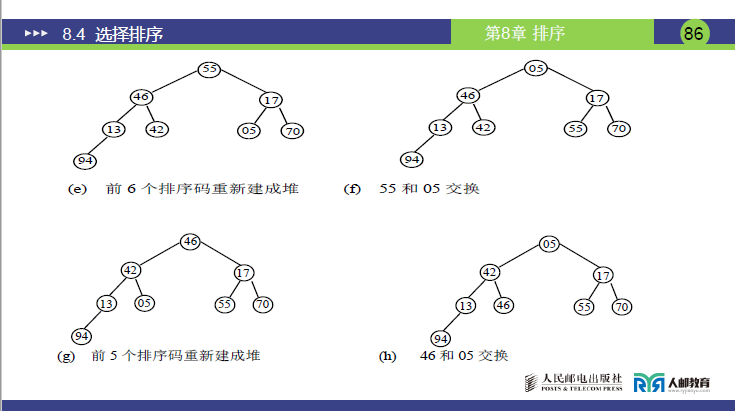
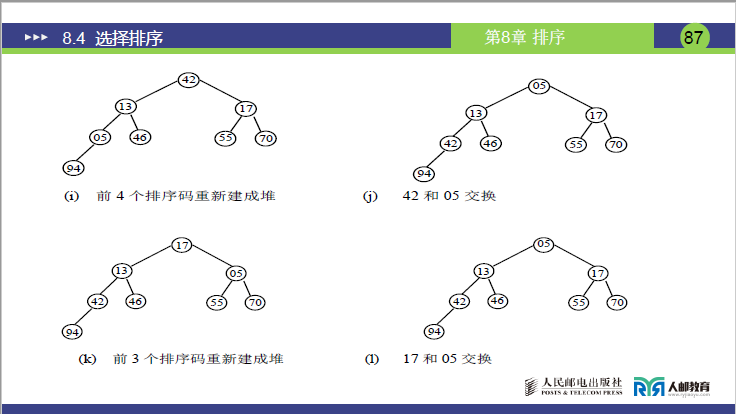
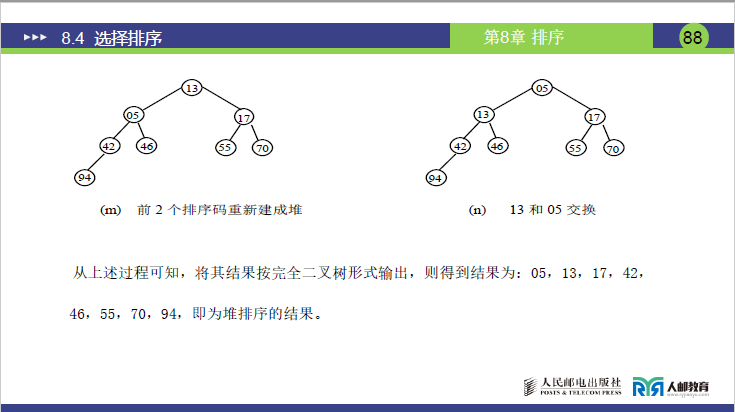
题目：待排序序列排序码为[46,55,13,42,94,05,17,70]，用大顶堆实现从小到大排序（对应课件 P83-88 图 (a)-(m)）。

步骤 1：建初堆（大顶堆）

1. 初始无序数组（索引 1-8）：[46,55,13,42,94,05,17,70]。
2. 最后一个非叶子节点⌊8/2⌋=4（节点 42），自下向上调整：
   • 调整节点 42（索引 4）：子节点 70（索引 8），42<70→交换→[46,55,13,70,94,05,17,42]。
   • 调整节点 13（索引 3）：子节点 05（索引 6）、17（索引 7），13<17→交换→[46,55,17,70,94,05,13,42]。
   • 调整节点 55（索引 2）：子节点 70（索引 4）、94（索引 5），55<94→交换→[46,94,17,70,55,05,13,42]。
   • 调整节点 46（索引 1）：子节点 94（索引 2）、17（索引 3），46<94→交换→[94,46,17,70,55,05,13,42]；节点 46（索引 2）的子节点 70（索引 4）>46→交换→[94,70,17,46,55,05,13,42]；节点 46（索引 4）的子节点 42（索引 8）<46→调整结束，大顶堆建成（堆顶 94 为最大值）。

步骤 2：堆排序循环（共 7 趟，每趟交换 + 调整）

趟数	操作 1：交换堆顶与未排序组末尾	操作 2：调整堆（恢复大顶堆）	未排序组长度	当前序列（已排序部分加粗）
1	堆顶 94 与末尾 42 交换→[42,70,17,46,55,05,13,94]	调整堆顶 42→[70,55,17,46,42,05,13,94]	7	[70,55,17,46,42,05,13,94]
2	堆顶 70 与末尾 13 交换→[13,55,17,46,42,05,70,94]	调整堆顶 13→[55,46,17,13,42,05,70,94]	6	[55,46,17,13,42,05,70,94]
3	堆顶 55 与末尾 05 交换→[05,46,17,13,42,55,70,94]	调整堆顶 05→[46,42,17,13,05,55,70,94]	5	[46,42,17,13,05,55,70,94]
4	堆顶 46 与末尾 05 交换→[05,42,17,13,46,55,70,94]	调整堆顶 05→[42,13,17,05,46,55,70,94]	4	[42,13,17,05,46,55,70,94]
5	堆顶 42 与末尾 05 交换→[05,13,17,42,46,55,70,94]	调整堆顶 05→[17,13,05,42,46,55,70,94]	3	[17,13,05,42,46,55,70,94]
6	堆顶 17 与末尾 05 交换→[05,13,17,42,46,55,70,94]	调整堆顶 05→[13,05,17,42,46,55,70,94]	2	[13,05,17,42,46,55,70,94]
7	堆顶 13 与末尾 05 交换→[05,13,17,42,46,55,70,94]	无需调整（仅 1 个元素）	1	[05,13,17,42,46,55,70,94]

最终有序序列

[05,13,17,42,46,55,70,94]（与课件 P88 结果一致）

（7）性能分析（课件 P89）

指标	具体分析
时间复杂度	建初堆需O(n)次比较，每趟调整堆需O(log2n)次比较，共n−1趟调整，总时间复杂度为O(nlog2n)（最好、最坏、平均均为此复杂度，稳定性优于快速排序）。
空间复杂度	仅需 1 个临时变量存储交换节点，无额外辅助空间，故空间复杂度为O(1)。
稳定性	不稳定。例：序列[2,1,2']，建大顶堆后堆顶 2 与末尾 2' 交换，得到[2',1,2]，原 2 与 2' 的相对次序改变。
讲课补充	堆排序是 “时间高效 + 空间高效” 的排序算法，适合数据量较大的场景（如百万级数据），是面试高频考点。

8.4.5 三种选择排序方法对比（汇总）

方法	时间复杂度	空间复杂度	稳定性	核心优势	核心劣势
简单选择排序	O(n2)	O(1)	不稳定	编程实现简单，交换次数少	时间复杂度高，仅适合小数据量
树型选择排序	O(nlog2n)	O(n)	稳定	时间复杂度低，逻辑直观	附加空间大，实用性低
堆排序	O(nlog2n)	O(1)	不稳定	时间 + 空间效率均优，适合大数据	实现复杂，需掌握堆的构建与调整

8.5 归并排序

8.5.1 归并排序概述

（1）归并排序的定义

归并排序（Merge Sort）的基本原理是：通过对两个或两个以上的有序结点序列的合并来实现排序（课件原文）。

归并排序是我们学习的第四类排序方法，前三类分别是插入排序（含直接插入、折半插入、希尔排序）、交换排序（含冒泡排序、快速排序）、选择排序（含简单选择、树型选择 / 锦标赛排序、堆排序）。归并排序的核心是 “合并有序序列”，通过将已有序的子序列合并，最终得到完整的有序序列，理解难度较低。

（2）常见的归并排序方法

根据合并的有序子序列数量，常见的归并排序方法分为两类（课件原文）：

• 2 - 路归并排序：每次合并两个有序子序列，是实际应用中最常用的归并排序方式。
• 多路归并排序：每次合并三个或三个以上的有序子序列（如三路归并、四路归并等）。

8.5.2 方法 1：2 - 路归并排序（对应课件 91-94 页）

（1）基本思想

2 - 路归并排序的核心思路是 “分治 + 递归”：

假设初始的待排序对象序列有 n 个数据对象，首先将其看成 n 个长度为 1 的有序子序列（因为单个元素本身就是有序的）；之后反复进行 “两两归并” 操作 —— 第一趟归并后得到 n/2 个长度为 2 的有序子序列（若 n 为奇数，则最后一个子序列长度仍为 1）；第二趟归并后得到 n/4 个长度为 4 的有序子序列；以此类推，直到最终合并成一个长度为 n 的有序序列（课件原文）。

老师补充：2 - 路归并的过程很直观，我们可以把初始数据放在一维数组中，每次只合并两个相邻的有序子序列，且始终按 “由小到大”（或指定排序规则）合并，子序列长度每趟翻倍，直到整个序列有序。

（2）算法步骤

2 - 路归并排序通过递归实现，具体步骤如下（课件原文）：

1. 分裂序列：将当前待排序序列（范围为low到high）一分为二，计算分裂点mid = ⌊(low + high)/2⌋（⌊⌋表示向下取整，即取中间位置左侧索引）。
2. 递归排序左子序列：对子序列R[low, mid]调用归并排序算法，将排序后的结果存入辅助数组S的S[low, mid]区间。
3. 递归排序右子序列：对子序列R[mid+1, high]调用归并排序算法，将排序后的结果存入辅助数组S的S[mid+1, high]区间。
4. 合并有序子序列：将辅助数组中两个有序子序列S[low, mid]和S[mid+1, high]合并，得到一个完整的有序序列，存入最终数组T[low, high]。

老师解释：递归的核心是 “先分后合”—— 先把大序列拆成最小的有序子序列（长度 1），再逐层合并回大的有序序列，合并操作是整个算法的关键。

（3）举例：2 - 路归并排序过程（对应课件 93 页 “二路归并排序过程” 图）

已知待排序排序码为：46, 55, 13, 42, 94, 05, 17, 70（共 8 个元素，按由小到大排序），具体排序过程如下（课件原文 + 老师详细讲解）：

①初始状态

将 8 个元素视为 8 个长度为 1 的有序子序列，即：

[46] [55] [13] [42] [94] [05] [17] [70]

（对应课件 93 页 “初始状态” 描述，每个括号内为一个有序子序列）

②第一趟归并（两两归并长度为 1 的子序列）

按顺序合并相邻的两个有序子序列，合并时按 “由小到大” 排序：

• [46]与[55]合并 → [46, 55]（46<55，直接按顺序排列）
• [13]与[42]合并 → [13, 42]（13<42，直接按顺序排列）
• [94]与[05]合并 → [05, 94]（05<94，交换顺序后排列）
• [17]与[70]合并 → [17, 70]（17<70，直接按顺序排列）

第一趟归并后得到 4 个长度为 2 的有序子序列：

[46, 55] [13, 42] [05, 94] [17, 70]

（对应课件 93 页 “一趟归并” 结果）

③第二趟归并（两两归并长度为 2 的子序列）

继续合并相邻的两个有序子序列：

• [46, 55]与[13, 42]合并：依次比较元素，13<42<46<55 → [13, 42, 46, 55]
• [05, 94]与[17, 70]合并：依次比较元素，05<17<70<94 → [05, 17, 70, 94]

第二趟归并后得到 2 个长度为 4 的有序子序列：

[13, 42, 46, 55] [05, 17, 70, 94]

（对应课件 93 页 “二趟归并” 结果）

④第三趟归并（合并长度为 4 的子序列）

合并最后两个有序子序列[13, 42, 46, 55]与[05, 17, 70, 94]：

依次比较两个子序列的元素，05<13<17<42<46<55<70<94 → 最终有序序列：

[05, 13, 17, 42, 46, 55, 70, 94]

（对应课件 93 页 “三趟归并” 结果，排序完成）

（4）性能分析

①时间复杂度

通常情况下，2 - 路归并排序的时间复杂度为O(n log₂n)（课件原文）。

原因：归并排序的 “分裂” 过程将序列拆分为 log₂n 层（如 8 个元素拆分为 3 层：8→4→2→1），每一层的 “合并” 操作需要遍历所有 n 个元素，因此总时间复杂度为 O (n × log₂n)，且最好、最坏、平均时间复杂度均为 O (n log₂n)，性能稳定。

②空间复杂度

2 - 路归并排序需要一个与原待排序对象数组同样大小的辅助数组（用于存储递归排序后的子序列和最终合并结果），因此空间复杂度为O(n)（课件原文）。

老师补充：这是 2 - 路归并排序的主要缺点 —— 空间开销较大，实际使用时需考虑内存是否充足。

③稳定性

2 - 路归并排序是稳定的排序方法（课件原文）。

原因：合并两个有序子序列时，若两个子序列中出现相同排序码（如子序列 A 含 “25”，子序列 B 含 “25”），会先复制前一个子序列中的 “25”，再复制后一个子序列中的 “25”，始终保持相同排序码的相对次序不变。

8.5.3 方法 2：多路归并排序

（1）定义

将三个或三个以上有序子区间合并成一个有序子区间的排序，称为多路归并排序（课件原文）。常见的有三路归并排序（合并三个有序子区间）、四路归并排序（合并四个有序子区间）等。

（2）实现思路

多路归并排序的核心逻辑与 2 - 路归并排序一致，都是 “分治 + 合并”—— 先将序列拆分为多个有序子区间，再逐步合并为完整有序序列；区别仅在于每次合并的子区间数量（由 2 个变为 3 个及以上）（课件原文）。

（3）说明

多路归并排序的原理和 2 - 路归并类似，但实现细节更复杂（如需要同时比较多个子区间的元素），且在大多数场景下，2 - 路归并排序的性能已能满足需求，因此实际应用中以 2 - 路归并排序为主，多路归并排序不再重点展开（课件原文 “在此，不再赘述”）。

8.6 基数排序

8.6.1 基数排序的定义

（1）核心内容

基数排序（Radix Sort）的基本原理：采用 “分配” 和 “收集” 的办法，用对多关键码进行排序的思想实现对单关键码进行排序的方法。

（2）补充讲解

• 基数排序是排序算法中的最后一类（前四类分别为插入排序、交换排序、选择排序、归并排序），前一类排序为归并排序（以二路归并为主）。
• 归并排序的特点：时间复杂度为O(nlog₂n)，稳定性好（关键字相等时相对次序不变），但缺点是需额外申请O(n)的辅助空间，而基数排序的 “分配 - 收集” 机制在空间开销上有不同特点。
• 实际应用中，基数排序的核心是将单关键码按 “位” 拆分（如个位、十位、百位），通过多轮 “按位分配 - 收集” 实现整体有序，类似生活中对数字的排序逻辑。

8.6.2 基数排序的算法步骤

（1） 核心内容

具体实现时，基数排序包含 “分配” 和 “收集” 两个核心操作，步骤如下：

1. 设待排序记录的关键字位数为d（如数字 123 的关键字位数d=3），依次对第k位（1≤k≤d）进行排序；
2. 分配：将第k位排序码相同的元素放到同一个队列中（队列按第k位排序码从小到大编号，如 0-9 对应数字的个位 / 十位 / 百位）；
3. 收集：按队列编号从小到大（如 0→9）依次取出队列中的元素，组成该趟排序后的结果，作为下一趟排序的输入。

（2）补充讲解

• 关键注意点：若待排序元素的关键字位数不同（如 9 是 1 位、78 是 2 位、123 是 3 位），需对高位补 0（不影响数值大小），统一为

  d

  位（取所有元素中最大的关键字位数）。例如：

  • 9 补为 009，78 补为 078，3 补为 003，7 补为 007，8 补为 008，68 补为 068，108 补为 108，309 补为 309，确保所有元素按 “相同位数” 参与每一轮分配。

• 队列特性：分配时使用 “先进先出”（FIFO）队列，保证相同排序码元素的相对次序不变，为基数排序的稳定性提供支持。

8.6.3 基数排序示例

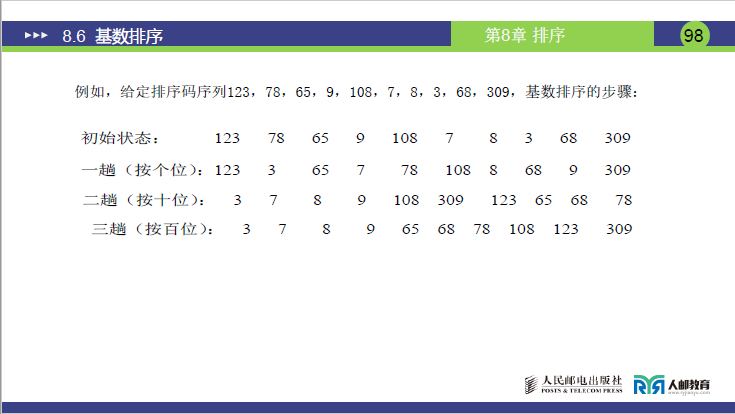
（1）初始条件

• 待排序排序码序列：123, 78, 65, 9, 108, 7, 8, 3, 68, 309（共 10 个元素）；

• 关键字最大位数d=3（如 123、309），每一位取值r=10（0-9），需进行 3 趟排序（按个位→十位→百位）；

• （图 1：初始状态，课件 98 页）

  | 初始状态 | 123 | 78 | 65 | 9 | 108 | 7 | 8 | 3 | 68 | 309 |

（2）第一趟：按个位分配与收集

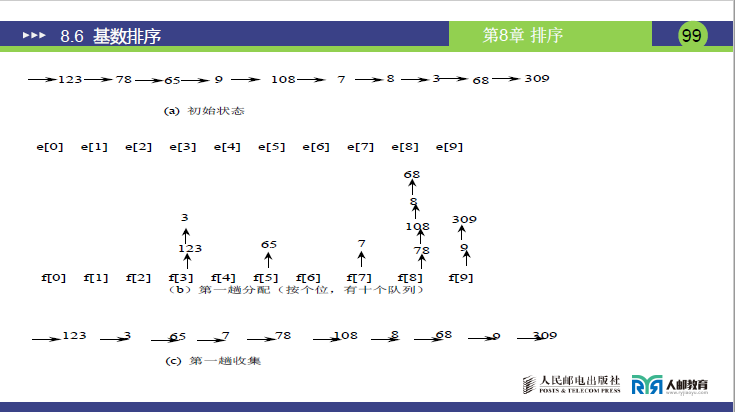
① 分配（按个位排序码，使用 10 个队列 F0-F9）

• 规则：提取每个元素的个位数字，放入对应编号的队列（F0 对应个位 0，F1 对应个位 1，…，F9 对应个位 9），相同个位按初始顺序入队；

• 具体分配过程（老师详细拆解）：

  • 123（个位 3）→ F3；
  • 78（个位 8）→ F8；
  • 65（个位 5）→ F5；
  • 9（个位 9，补 0 后 009）→ F9；
  • 108（个位 8）→ F8（接在 78 之后，保持初始顺序）；
  • 7（个位 7，补 0 后 007）→ F7；
  • 8（个位 8，补 0 后 008）→ F8（接在 108 之后）；
  • 3（个位 3，补 0 后 003）→ F3（接在 123 之后）；
  • 68（个位 8，补 0 后 068）→ F8（接在 8 之后）；
  • 309（个位 9，补 0 后 309）→ F9（接在 9 之后）；

• （图 2：第一趟分配结果，课件 99 页图 b）

  | 队列编号 | F0（空） | F1（空） | F2（空） | F3（123→3） | F4（空） | F5（65） | F6（空） | F7（7） | F8（78→108→8→68） | F9（9→309） |

② 收集（按队列编号 F0→F9 依次取元素）

• 收集结果：123, 3, 65, 7, 78, 108, 8, 68, 9, 309；

• （图 3：第一趟收集结果，课件 99 页图 c）

  | 第一趟收集结果 | 123 | 3 | 65 | 7 | 78 | 108 | 8 | 68 | 9 | 309 |

（3） 第二趟：按十位分配与收集

①分配（按十位排序码，基于第一趟收集结果，补 0 后提取十位）

• 补 0 后序列：123（123）、3（003）、65（065）、7（007）、78（078）、108（108）、8（008）、68（068）、9（009）、309（309）；

• 规则：提取每个元素的十位数字，放入对应队列 F0-F9；

• 具体分配过程：

  • 123（十位 2）→ F2；
  • 003（十位 0）→ F0；
  • 065（十位 6）→ F6；
  • 007（十位 0）→ F0（接在 003 之后）；
  • 078（十位 7）→ F7；
  • 108（十位 0）→ F0（接在 007 之后）；
  • 008（十位 0）→ F0（接在 108 之后）；
  • 068（十位 6）→ F6（接在 065 之后）；
  • 009（十位 0）→ F0（接在 008 之后）；
  • 309（十位 0）→ F0（接在 009 之后）；

• （图 4：第二趟分配结果，课件 100 页图 d）

  | 队列编号 | F0（003→007→108→008→009→309） | F1（空） | F2（123） | F3（空） | F4（空） | F5（空） | F6（065→068） | F7（078） | F8（空） | F9（空） |

② 收集（按 F0→F9 取元素）

• 收集结果：3, 7, 108, 8, 9, 309, 123, 65, 68, 78；

• （图 5：第二趟收集结果，课件 100 页图 e）

  | 第二趟收集结果 | 3 | 7 | 108 | 8 | 9 | 309 | 123 | 65 | 68 | 78 |

（4）第三趟：按百位分配与收集

① 分配（按百位排序码，基于第二趟收集结果，补 0 后提取百位）

• 补 0 后序列：3（003）、7（007）、108（108）、8（008）、9（009）、309（309）、123（123）、65（065）、68（068）、78（078）；

• 规则：提取每个元素的百位数字，放入对应队列 F0-F9；

• 具体分配过程：

  • 003（百位 0）→ F0；
  • 007（百位 0）→ F0（接在 003 之后）；
  • 108（百位 1）→ F1；
  • 008（百位 0）→ F0（接在 007 之后）；
  • 009（百位 0）→ F0（接在 008 之后）；
  • 309（百位 3）→ F3；
  • 123（百位 1）→ F1（接在 108 之后）；
  • 065（百位 0）→ F0（接在 009 之后）；
  • 068（百位 0）→ F0（接在 065 之后）；
  • 078（百位 0）→ F0（接在 068 之后）；

• （图 6：第三趟分配结果，课件 101 页图 f）

  | 队列编号 | F0（003→007→008→009→065→068→078） | F1（108→123） | F2（空） | F3（309） | F4-F9（空） |

② 收集（按 F0→F9 取元素）

• 收集结果（最终有序序列）：3, 7, 8, 9, 65, 68, 78, 108, 123, 309；

• （图 7：第三趟收集结果，课件 101 页图 g）

  | 最终有序序列 | 3 | 7 | 8 | 9 | 65 | 68 | 78 | 108 | 123 | 309 |

8.6.4 基数排序的性能分析

（1）课件核心内容

性能指标	具体分析
时间复杂度	O(d(n+r))，其中：- d：关键字位数（如 3 位数字d=3）；- n：待排序元素个数；- r：每一位排序码的取值数（如数字 0-9，r=10）；每趟分配时间O(n)，每趟收集时间O(r)，共d趟，总时间为d×(O(n)+O(r))=O(d(n+r))。
空间复杂度	O(n+2r)，其中：- 2r：10 个队列的头指针（F0-F9）和尾指针（e0-e9），共2r个链表指针；- n：存储待排序元素的指针域空间（需记录元素间的连接关系）。
稳定性	稳定。分配时按 “先进先出” 原则，相同排序码元素的相对次序在收集后保持不变（如示例中 78 和 108 的个位均为 8，分配后 78 在前、108 在后，收集后次序不变）。

（2）补充讲解

• 基数排序的时间效率与d（关键字位数）密切相关：若待排序元素为整数，d由最大元素的位数决定（如最大元素为 999，d=3），当d较小时（如数据范围不大），时间复杂度接近O(n)，适合大规模数据排序；
• 空间开销特点：相较于归并排序的O(n)辅助空间，基数排序需额外维护2r个指针，但r通常较小（如r=10），因此空间开销主要由n决定，与归并排序相近。

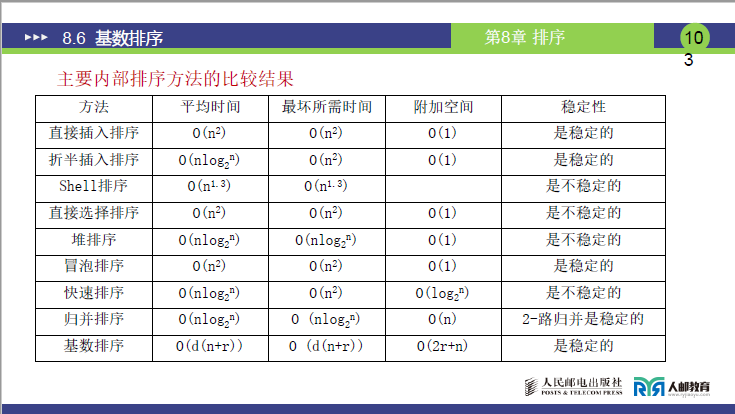
8.6.5 主要内部排序方法的比较

（1）综合对比表

（2）补充对比表

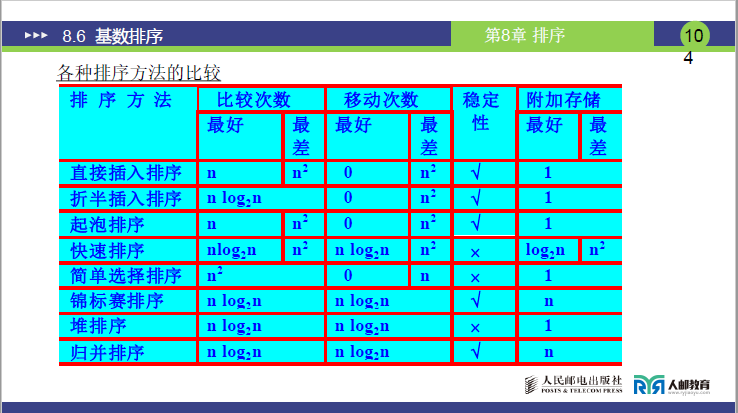
（3）总结

• 稳定排序方法：直接插入、折半插入、冒泡、归并（2 - 路）、基数排序，适合对 “相同关键字相对次序有要求” 的场景（如按成绩排序后需保持同分数学生的原始报名次序）；
• 高效排序方法（平均时间O(nlog₂n)或接近O(n)）：快速排序、堆排序、归并排序、基数排序，适合大规模数据；
• 原地排序（附加空间O(1)）：直接插入、折半插入、希尔、直接选择、堆排序、冒泡排序，适合内存有限的场景。

参考资料：教材《数据结构 C 语言 第 3 版》 数据结构考研指导（基础篇） 、数据结构考研指导（基础篇） 视频课程｜赵海英