第7章查找

第7章查找

7.1 查找的基本概念

7.1.1 查找的目的

（1）核心定义

所谓查找（Searching），是指在一个含有众多的数据元素（或记录）的查找表中，找出某个特定的数据元素（或记录） 的过程。

• 核心前提：数据集合必须是 “同一类型”，例如 “学生信息集合”（每个元素都是 “学生” 类型，含学号、姓名、成绩等字段）、“商品库存集合”（每个元素都是 “商品” 类型，含编号、名称、价格等字段），不同类型数据无法在同一集合中查找；
• 查找目标：既可以是单个 “数据元素”（如完整的学生信息），也可以是 “记录”（数据元素的别称，在数据库或表结构场景中常用 “记录” 描述，如 “一条学生记录”）
• 定义强调 “过程性”：查找不是 “结果”，而是 “从表中定位特定目标的操作流程”，流程可能成功（找到目标）或失败（未找到目标）；
• 与 “查找目的” 的区别：目的是 “找所需元素”，定义是 “找元素的过程”，前者是目标，后者是实现目标的动作。

7.1.2 查找的分类（按 3 个维度划分，衔接后续章节）

（1）按 “查找算法依赖的结构” 分（核心分类，讲课 + 课件一致）

这是第七章的核心脉络，后续 3 节分别对应这三类查找的具体实现：

• ① 线性表的查找（7.2 内容）
  • 基于 “线性结构”（顺序表、单链表）实现，属于静态查找（部分可扩展为动态）。
  • 后续重点：顺序查找、折半查找（二分查找）、分块查找。
• ② 树表的查找（7.3 内容，修正讲课 “数表” 为 “树表”）
  • 基于 “树形结构”（二叉树、多叉树）实现，属于动态查找（支持增删）。
  • 后续重点：二叉排序树查找、平衡二叉树查找、B - 树与 B + 树查找。
• ③ 散列表的查找（哈希表）（7.4 内容，修正讲课 “希表” 为 “散列表”）
  • 基于 “散列函数” 直接计算存储地址，不依赖比较，兼顾静态与动态。
  • 后续重点：散列函数构造、冲突解决方法（开放地址法、链地址法）。

（2）按 “查找表是否可修改” 分（即静态 / 动态查找，见 2.2 术语）

• 核心区别：是否对查找表进行 “增删操作”。
  • 静态：仅 “查”，不增删（如历史数据查询）；
  • 动态：“查 + 增删”，找不到则插入（如实时数据维护）。

（3）按 “查找表存储位置” 分（即内部 / 外部查找，见 2.2 术语）

• 核心区别：存储介质不同。
  • 内部：内存（速度快，数据量小）；
  • 外部：外存（速度慢，数据量大，需考虑 IO 效率）。

7.1.3 必须掌握的核心术语

术语是理解后续算法的关键，需区分清楚 “定义” 与 “作用”：

术语	讲课表述核心	课件补充与规范解析	例子
数据元素（记录）	数据集按行叫数据元素，又称记录	数据元素是组成数据结构的基本单位，“记录” 是数据元素在 “查找场景” 下的别称（侧重结构化数据）	学生表中一行 “学号 01 + 姓名张三” 是 1 条记录
关键字（Key）	查找的某一个字段	用于标识数据元素（记录）的特定字段，是查找的 “匹配依据”	按 “学号” 查学生，学号就是关键字
主关键字（Primary Key）	决定一行唯一的字段	唯一标识一条记录的关键字（一个记录仅 1 个主关键字），无重复值	身份证号、学号（唯一）
次关键字（Secondary Key）	非主关键字的字段	不能唯一标识记录的关键字（可重复），用于辅助查找	性别、班级（同一班级有多个学生）
查找表（Search Table）	存放待查找数据的集合	由同一类型的记录构成的集合，是查找操作的 “载体”	学生信息表、员工工资表
静态查找（Static Search）	找不到返回失败	查找过程中不修改查找表（仅查询，不增删记录）；查找表可存为顺序表或单链表	查历史成绩表（成绩不修改）
动态查找（Dynamic Search）	找不到则插入记录	查找过程中可修改查找表（找不到时插入，找到时可删除）；查找表多存为树表或散列表	查实时购物车（没找到的商品可加入）
内部查找（Internal Search）	内存中的查找	查找表存储在内存中，速度快；后续 7.2、7.3 主要讲内部查找	内存数组中的查找
外部查找（External Search）	外存中的查找	查找表存储在磁盘、U 盘等外存中，速度慢；为后续排序（外排序）铺垫，如磁盘文件查找	查电脑 D 盘下的 Excel 表格数据

7.1.4 查找算法的性能衡量指标：平均查找长度（ASL）

（1）为什么用 ASL？（讲课重点强调）

• 讲课提到：“查找的时间复杂度不常用大 O 法、频度法（修正讲课 “平度法” 为 “频度法”），而是用 ASL”。
• 原因：大 O 法是 “宏观复杂度”（如顺序查找 O (n)），ASL 是 “微观具体指标”—— 通过 “比较次数的期望值” 精准衡量查找效率，更贴合查找算法的实际性能。

（2）ASL 的定义与公式（讲课 + 课件推导）

• 定义：给定待查找关键字与查找表中关键字的比较次数的期望值，称为平均查找长度，简称 ASL。

• 核心公式：\(ASL = \sum_{i=1}^{n} p_i \times c_i\)

  其中：

  • n：查找表中记录的个数；
  • p_i：查找第i条记录的概率（\(\sum_{i=1}^{n} p_i = 1\)）；
  • c_i：查找第i条记录成功时，关键字的比较次数。

（3）常见场景：等概率查找（课件补充计算）

• 实际中若未说明概率，默认 “等概率查找”（即每条记录被查找的概率相等）：\(p_i = \frac{1}{n} (i = 1, 2, \dots, n)\)

• 此时公式简化为：\(ASL = \frac{1}{n} \sum_{i=1}^{n} c_i\)

（4）例子：快速理解 ASL 计算

假设查找表中有 3 条记录（R1、R2、R3），等概率查找，查找成功时的比较次数分别为c1=1（第 1 个元素，1 次比较）、c2=2（第 2 个元素，2 次比较）、c3=3（第 3 个元素，3 次比较）：

ASL=31×(1+2+3)=2

即平均需要 2 次比较就能找到目标记录。

7.1.5 查找的属性（静态查找与动态查找的详细区分）

（1）静态查找

• 课件核心定义：对查找表实施静态查找时，查找表的组织结构可以是顺序表结构，也可以是单链表结构；若表中存在关键字值等于k**ey的记录，则查找成功；否则表示查找失败（不修改查找表）。
• 讲课内容补充：
  • 本质：“只读” 式查找，查找过程中不改变查找表的内容和结构，仅返回 “成功 / 失败” 及目标位置（若成功）；
  • 适用场景：查找表数据固定不变的场景，如 “历年高考分数线查找”“历史订单记录查询”（数据不会新增或删除）。

（2）动态查找

• 课件核心定义：在查找表中实施查找时，对于给定值k**ey，若表中存在关键字值等于k**ey的记录，则查找成功；否则将待查找记录按规则插入查找表中（修改查找表）。
• 讲课内容补充：
  • 本质：“可写” 式查找，查找过程中可能修改查找表（插入未找到的记录，后续也可支持删除），查找表的内容和结构会随查找操作动态变化；
  • 适用场景：查找表数据需动态更新的场景，如 “实时商品库存查找”（新商品需插入表中）、“用户注册信息查找”（新用户需插入表中）。

（3）静态与动态查找的核心区别（总结）

对比维度	静态查找	动态查找
查找表是否修改	不修改（固定）	可能修改（插入 / 删除，动态）
结果返回形式	成功（目标位置）/ 失败	成功（目标位置）/ 失败（插入）
表结构支持	顺序表、单链表等静态结构	树表、哈希表等动态结构
典型应用场景	历史数据查询	实时数据查询与更新

易错点纠正与辨析

1. 主关键字 vs 次关键字：唯一与否是关键
   • 易错点：认为 “次关键字也能唯一标识记录”。
   • 辨析：主关键字唯一（如身份证号），次关键字可重复（如 “姓名” 可能重名），这是区分两者的核心。
2. 动态查找的核心：“找不到就插入”，而非 “找到就修改”
   • 易错点：把 “动态查找” 理解为 “找到记录后修改其值”。
   • 辨析：动态查找的 “动态” 体现在 “查找表的大小可变化”（找不到时插入新记录，找到时可删除旧记录），修改记录值不属于动态查找的定义范畴。

本节核心总结

1. 3 个核心术语：关键字（查找依据）、查找表（载体）、ASL（性能指标）；
2. 1 个核心公式：\(ASL = \sum_{i=1}^{n} p_i \times c_i\)（等概率下简化为\(\frac{1}{n} \sum_{i=1}^{n} c_i\)）；
3. 3 类查找算法：线性表、树表、散列表（后续章节逐一展开）；
4. 1 个关键区别：静态查找（不修改表）vs 动态查找（可增删表）。

7.2 线性表的查找

章节概览

　　7.2 线性表的查找是静态查找（查找过程中不改变查找表结构）的核心内容，是后续树表、散列表查找的基础。其核心框架围绕两种经典方法展开：顺序查找（适用于简单场景）和折半查找（适用于高效场景），需重点掌握两种方法的思想、过程、性能分析及适用场景，尤其关注平均查找长度（ASL） 的计算（查找性能的核心衡量指标）。

7.2.1顺序查找（Sequential Search）

（1）查找思想（课件 9 页）

• 核心逻辑：用待查找元素（或其关键字）与查找表中的元素逐个依次比较，若找到关键字相等的元素，则查找成功；若遍历完所有元素仍未找到，则查找失败。

• 老师补充示例：生活中 “找座位” 就是典型的顺序查找 —— 座位按 1、2、3…n 顺序排列，从第 1 个座位开始逐个核对，直到找到自己的座位（成功）或确认没有目标座位（失败）。

• 表结构要求：顺序查找是最基础的查找方法，无任何前提限制：

  • 表结构：数组、链表均可；

  • 数据顺序：有序、无序均可；

  • 核心场景：数据量较小（如n≤100）或表结构频繁变动（插入 / 删除后无需维护顺序）的场景。

（2）过程举例（课件无单独图，结合老师讲解补充）

①核心思想

假设查找表为顺序表[15, 28, 36, 42, 57]（n=5），目标元素为36：

1. 比较第 1 个元素15：15≠36，继续；
2. 比较第 2 个元素28：28≠36，继续；
3. 比较第 3 个元素36：36=36，查找成功，共比较 3 次。

若目标元素为60：

1. 依次比较15、28、36、42、57，均不相等；
2. 遍历结束，查找失败，共比较 5 次（等于表长 n）。

（3）扫描方向补充（重点）

顺序查找有两种扫描方式，最终 ASL 结果一致，但实现细节不同：

• 从前往后：第i个元素（i=1~n）的比较次数c_i=i（第 1 个比 1 次，第 2 个比 2 次…）；

• 从后往前：第i个元素的比较次数c_i=n-i+1（最后 1 个比 1 次，倒数第 2 个比 2 次…）；

  两种方式的核心是 “逐个遍历”，差异仅在于遍历起点，不影响性能。

7.2.2性能分析（关键：平均查找长度 ASL）

在数据结构中，查找的性能主要通过平均查找长度（Average Search Length，ASL） 衡量，ASL 指 “所有查找情况的比较次数的平均值”，需分 “查找成功” 和 “查找失败” 两种场景分析（默认 “每个元素被查找的概率相等”）。

（1）查找成功时的 ASL

• 核心公式：\(ASL_{success} = \sum_{i=1}^{n} p_i \times c_i\)

  代入p_i=1/n、c_i=i（以从前往后扫描为例）：

  \(ASL_{success} = \sum_{i=1}^{n} \frac{1}{n} \times i = \frac{1}{n}(1 \times 1 + 1 \times 2 + \dots + 1 \times n) = \frac{1}{n} \times \frac{n(n+1)}{2} = \frac{n+1}{2}\)

• 结论：成功时平均需比较(n+1)/2次，如n=10时，ASL_success=5.5。

（2）查找失败时的 ASL

• 场景：遍历完所有n个元素仍未找到K，需比较n次（从前往后）或n次（从后往前）；
• 结论：ASL_failure = n（如n=10时，失败需比较 10 次）。

（3）时间复杂度与空间复杂度

• 时间复杂度：O(n)（比较次数与元素个数n成线性关系，n越大效率越低）。
• 空间复杂度：O(1)（无需额外空间存储辅助数据，仅用变量记录当前比对位置）。

（4）优缺点

优点	缺点
1. 算法简单，易实现； 2. 对表结构无要求（数组 / 链表、有序 / 无序均可）； 3. 适合小规模数据（n较小时效率可接受）。	1. 效率低，n较大时（如n>1000）ASL 急剧增大； 2. 未利用数据的有序性（若表有序，顺序查找也无法优化）。

（5）优缺点

在查找成功时的ASL为:\(ASL_{success} = \sum_{i=1}^{n} p_i \times c_i\)

顺序查找的优点是算法简单，对表结构无任何要求，无论是用向量（相当于数组）还是用链表来存放结点，也无论结点之间是否按关键字有序或无序，它都同样适用。顺序查找的缺点是查找效率低，ASL达到了(n+1)/2 ，所以时间复杂度为O(n)。当n较大时，不宜采用顺序查找，而必须寻求更好的查找方法。

7.2.3折半查找（Binary Search）

（1）定义与严格前提

折半查找又称 “二分查找”，是高效静态查找方法，但有两个不可突破的前提：

• 表结构：必须是顺序存储（如数组）—— 需随机访问中间元素，链表无法满足；
• 数据顺序：必须是有序表（从小到大或从大到小，课堂默认 “从小到大”）。

（2）核心思想与详细实例

①核心思想

​ 折半查找(Binary Search)是用待查找元素的key与查找表的“中间位置”的元素的关键字进行比较，若它们的值相等，则查找成功。若查找元素key大于查找表的“中间位置”的元素的关键字的值，则在查找表的中间位置的后端范围内，继续使用折半查找。否则，则在查找表的中间位置的前端范围内，继续使用折半查找。直到查找成功或者失败为止。

通过 “二分缩小范围” 减少比较次数，步骤如下：

1. 初始化：用low（指向查找范围起点，初始low=1）、high（指向范围终点，初始high=n）、mid（指向范围中点，mid=(low+high)//2，//表示向下取整，符合 C 语言整数除法规则）；
2. 循环比较：
   • 若K == 元素[mid]：查找成功，返回mid；
   • 若K > 元素[mid]：K在mid右侧，调整low=mid+1；
   • 若K < 元素[mid]：K在mid左侧，调整high=mid-1；
3. 终止条件：若low > high，查找范围为空，返回失败。

②课堂 + 课件实例（有序表[8,17,25,44,68,77,98,100,115,125]，n=10）

实例 1：查找K=17（成功）

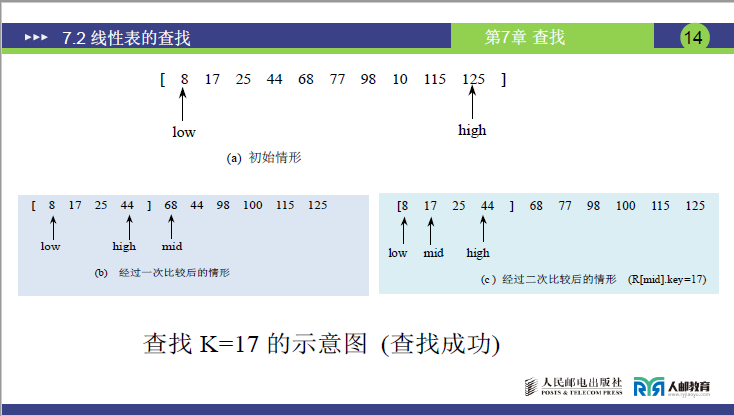
步骤	low	high	mid=(low+high)//2	元素 [mid]	比较结果（K=17）	范围调整
初始化	1	10	5	68	17 < 68	调整 high=mid-1=4
第 1 次比较	1	4	2	17	17 == 17	查找成功

• 结论：共比较 2 次，成功返回位置 2。

实例 2：查找K=120（失败）

步骤	low	high	mid=(low+high)//2	元素 [mid]	比较结果（K=120）	范围调整
初始化	1	10	5	68	120 > 68	调整 low=mid+1=6
第 1 次比较	6	10	8	100	120 > 100	调整 low=mid+1=9
第 2 次比较	9	10	9	115	120 > 115	调整 low=mid+1=10
第 3 次比较	10	10	10	125	120 < 125	调整 high=mid-1=9
终止	10	9	-	-	low > high	查找失败

• 结论：共比较 4 次，确认K=120不存在。

（3）性能分析（判定树为核心工具）

​ 为了分析二分查找的性能，可以用二叉树来描述二分查找过程。把当前查找区间的中点作为根结点，左子区间和右子区间分别作为根的左子树和右子树，左子区间和右子区间再按类似的方法，由此得到的二叉树称为二分查找的判定树。例如，给定的关键字序列8，17，25，44，68，77，98，100，115，125，它的判定树是什么？

课件明确指出：折半查找的过程可通过判定树可视化，树的结构直接决定 ASL—— 每个节点代表一次比较，树的层数对应比较次数。

①判定树的构建规则（课件定义）

• 根节点：第一次比较的mid元素（如n=10时，根节点为 68）；
• 左子树：K < mid时的查找范围（左侧元素），右子树：K > mid时的查找范围（右侧元素）；
• 叶子节点：查找失败的情况（无对应元素，共n+1个）。

②n=10时的判定树结构

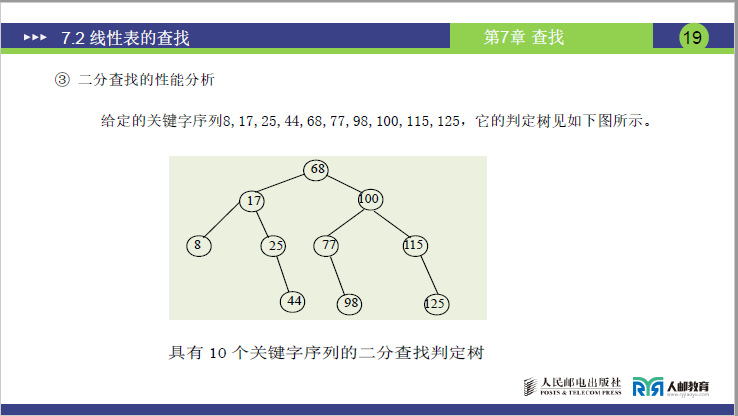
        68（第1层，比较1次）
       /   \
    17（2）  100（2）（第2层，比较2次）
   /  \     /   \
 8（3）25（3）77（3）115（3）（第3层，比较3次）
        \     \      \
       44（4）98（4）125（4）（第4层，比较4次）

• 各层节点数：第k层最多2^(k-1)个节点（符合完全二叉树特性）；
• 比较次数：节点所在层数 = 该元素的比较次数。

③查找成功时的 ASL

​ 从②中图可知，查找根结点68，需一次查找，查找17和100，各需二次查找，查找8、25、77、115各需三次查找，查找44、98、125各需四次查找。因此，可以得到结论：二叉树第K层结点的查找次数各为k次(根结点为第1层)，而第k层结点数最多为2^k-1个。假设该二叉树的深度为h，则二分查找的成功的平均查找长度为（假设每个结点的查找概率相
等）：

\[ASL_{success} = \sum_{i=1}^{n} p_i \times c_i = \frac{1}{n} \sum_{i=1}^{n} c_i \le \frac{1}{n}(1 \times 2^0 + 2 \times 2^1 + 3 \times 2^2 + \dots + h \times 2^{h-1}) \]

​ 因此，在最坏情形下，上面的不等号将会成立，并根据二叉树的性质，最大的结点数n=2^h-1，h=log₂(n+1) ，于是可以得到平均查找长度\(ASL=\frac{n+1}{n}log_2(n+1)-1\)

。该公式可以按如下方法推出：

\[\ \begin{aligned} \text{设 } s &= \sum_{k=1}^{h} k 2^{k-1} = 2^0 + 2 \cdot 2^1 + 3 \cdot 2^2 + \dots + (h-1) \cdot 2^{h-2} + h \cdot 2^{h-1} \\ \text{则 } 2s &= 2^1 + 2 \cdot 2^2 + \dots + (h-2) \cdot 2^{h-2} + (h-1) \cdot 2^{h-1} + h \cdot 2^h \\ s &= 2s - s \\ &= h \cdot 2^h - (2^0 + 2^1 + 2^2 + \dots + 2^{h-2} + 2^{h-1}) \\ &= h \cdot 2^h - (2^h - 1) \\ &= \log_2(n+1) \cdot (n+1) - n \end{aligned} \]

图里的最后一步发生了变量代换，它是基于满二叉树的性质：

• \(n = 2^h - 1\) （\(h\) 层满二叉树的总节点数 \(n\)）
• 所以推导出 \(2^h = n+1\) 和 \(h = \log_2(n+1)\)

当n很大时，ASL_success≈log₂(n+1)−1 可以作为二分查找成功时的平均查找长度，它的时间复杂度为O(log₂n)。

• 等概率假设下，ASL_success = （各元素比较数之和）/ n代入n=10的判定树：

  ASL_success=(1×1+2×2+3×4+4×3)/10=(1+4+12+12)/10=2.9

• 通用公式（课件结论）：

  若判定树高度为h（h=⌈log₂(n+1)⌉，⌈⌉表示向上取整），则：ASL_success≈log₂(n+1)−1

  时间复杂度为O(log₂n)（远优于顺序查找的O(n)）。

④查找失败时的 ASL（课件补充）

• 失败节点共n+1=11个，比较次数为对应父节点的层数：

  第 2 层对应 2 个失败节点（比较 2 次），第 3 层对应 4 个（比较 3 次），第 4 层对应 5 个（比较 4 次）；

  代入计算：

  ASL_failure=(2×2+3×4+4×5)/11≈3.27

（4）优缺点（课件 + 课堂总结）

优点	缺点
1. 效率高，时间复杂度O(log₂n)，n越大优势越明显（如n=1000时，最多比较 10 次）； 2. 空间复杂度O(1)，仅需 3 个指针变量（low, high, mid）。	1. 前提严格：必须是 “有序 + 顺序存储”，链表无法使用； 2. 表结构变动成本高（插入 / 删除后需重新排序，破坏有序性）； 3. 小规模数据时，优势不明显（对比顺序查找，实现稍复杂）。

7.2.4顺序查找与折半查找对比（课件核心差异）

对比维度	顺序查找	折半查找
前提条件	无（数组 / 链表、有序 / 无序均可）	有序表 + 顺序存储（数组）
核心逻辑	逐个比对	二分缩小范围
成功 ASL	(n+1)/2（线性）	≈log₂(n+1)-1（对数）
时间复杂度	O(n)	O(log₂n)
空间复杂度	O(1)	O(1)
适用场景	小规模数据、表结构频繁变动	大规模静态有序数据
链表兼容性	兼容（支持逐个遍历）	不兼容（无法随机访问 mid）

7.2.5课堂考试与应用提示（课件 + 老师重点强调）

1. 术语规范：考试中 “折半查找” 为标准术语，“二分查找” 可通用，但需避免老师口误的 “泽曼查找”“banner search”（正确为 “Binary Search”）；
2. 折半查找高频考点：
   • 查找过程描述：需写出low, high, mid的每次调整值（如实例中的步骤表）；
   • 判定树绘制：按 “根为 mid，左小右大” 规则，明确各层节点及比较次数；
   • ASL 计算：结合判定树，代入等概率公式求解；
3. 易错点：折半查找的mid计算需 “向下取整”，终止条件为low > high（而非low == high）；
4. 实际应用：若数据需 “频繁查找 + 偶尔变动”，优先选折半查找（维护有序性成本可接受）；若 “频繁变动 + 少量查找”，选顺序查找（无需维护顺序）。

7.3 树的查找

章节概述：树表查找的定位

​ 树表查找是动态查找的核心实现方式，与 7.2 节 “线性表的静态查找”（查找失败不修改表结构）本质区别在于：

• 动态查找特性：若查找表中存在关键字等于目标值的记录，则查找成功；若不存在，则将目标记录按规则插入表中（表结构随查找过程动态变化）。
• 核心优势：解决线性表查找（如顺序查找 O (n)、折半查找依赖有序表且无法动态插入）在 “大规模数据 + 动态更新” 场景下的效率问题，通过树型结构控制查找深度，降低时间复杂度。

树表查找（1）重点讲解两类基础树结构：二叉排序树（基础动态查找树）和平衡二叉树（解决二叉排序树不平衡问题的优化结构）。

树表查找是一种动态查找，包括三种方法。

• 方法1：二叉排序树查找
• 方法2：平衡二叉树查找
• 方法3：B-树 B+树

7.3.1法 1：二叉排序树查找（Binary Search Tree, BST）

（1）前提条件

需将查找表组织为二叉排序树，树的结构满足 “二叉排序树性质”：

• 若左子树非空，则左子树中所有节点的关键字小于根节点的关键字；
• 若右子树非空，则右子树中所有节点的关键字大于根节点的关键字；
• 左、右子树本身也需满足二叉排序树性质。

（2）核心思想（查找过程）

​ 若二叉排树为空，则查找失败，否则，先拿根结点值与待查值进行比较，若相等，则查找成功，若根结点值大于待查值，则进入左子树重复此步骤，否则，进入右子树重复此步骤，若在查找过程中遇到二叉排序树的叶子结点时，还没有找到待找结点，则查找不成功。

遵循 “比根大找右，比根小找左” 的递归 / 迭代逻辑，步骤如下：

1. 若二叉排序树为空 → 查找失败；
2. 若目标关键字key等于根节点关键字 → 查找成功；
3. 若key < 根节点关键字 → 递归查找左子树；
4. 若key > 根节点关键字 → 递归查找右子树；
5. 若遍历至叶子节点仍未匹配 → 查找失败（此时需将key插入树中，维持二叉排序树性质）。

（3）二叉排序树的构建示例

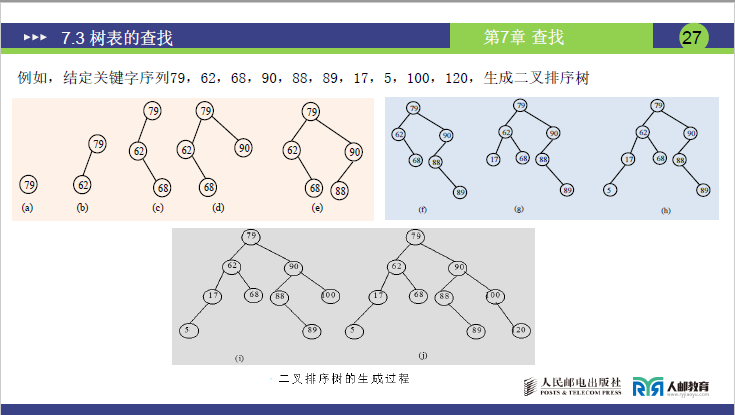
例如，结定关键字序列79，62，68，90，88，89，17，5，100，120，生成二叉排序树过程如下图所示。（注：二叉排序树与关键字排列顺序有关，排列顺序不一样，得到的二叉排序树也不一样）

构建过程体现 “动态插入” 特性：

插入顺序	核心操作	树结构变化
1. 插入 79	空树 → 79 为根节点	根：79（无左右子树）
2. 插入 62	62 < 79 → 作为 79 左子树	79 左孩子：62
3. 插入 68	68 <79 → 进入左子树；68> 62 → 作为 62 右子树	62 右孩子：68
4. 插入 90	90 > 79 → 作为 79 右子树	79 右孩子：90
5. 插入 88	88 > 79 → 进入右子树；88 < 90 → 作为 90 左子树	90 左孩子：88
6. 插入 89	89 > 79 → 进入右子树；89 <90 → 进入左子树；89> 88 → 作为 88 右子树	88 右孩子：89
7. 插入 17	17 < 79 → 进入左子树；17 < 62 → 作为 62 左子树	62 左孩子：17
8. 插入 5	5 < 79 → 进入左子树；5 < 62 → 进入左子树；5 < 17 → 作为 17 左子树	17 左孩子：5
9. 插入 100	100 > 79 → 进入右子树；100 > 90 → 作为 90 右子树	90 右孩子：100
10. 插入 120	120 > 79 → 进入右子树；120 > 90 → 进入右子树；120 > 100 → 作为 100 右子树	100 右孩子：120

⚠️ 关键结论：二叉排序树的结构依赖关键字插入顺序—— 若插入序列有序（如从小到大5,17,62,...120），树会退化为单链表（左子树为空，仅右子树延伸）。

（4）性能分析（基于 ASL 和时间复杂度）

①平均查找长度（ASL）

​ 在二叉排序树查找中，成功的查找次数不会超过二叉树的深度，而具有n个结点的二叉排序树的深度，最多为log₂n，最坏为n。因此，二叉排序树查找的最好时间复杂度为O(log₂n)，最坏的时间复杂度为O(n)，一般情形下，其时间复杂度大致可看成O(log₂n)，比顺序查找效率要好，但比二分查找要差。

查找成功的 ASL 计算公式：\(ASL = \sum_{i=1}^{n} p_i \times c_i\)（第i个节点的查找概率p_i ， 查找该节点的比较次数c_i）\(ASL = \sum_{i=1}^{n} p_i \times c_i\)

• 假设所有节点查找概率相等（p_i = 1/n，n 为节点数），则$ASL = \frac{1}{n} \sum_{i=1}^{n} c_i $；
• 比较次数c_i=节点所在的 “树的深度”（根节点深度为 1，子节点深度 = 父节点深度 + 1）。

②时间复杂度

最好情况：树结构平衡（近似完全二叉树），深度为log₂n，此时ASL ≈ log₂n，时间复杂度O(log₂n)；
最坏情况：树退化为单链表（如有序插入），深度为n，此时ASL = (n+1)/2，时间复杂度O(n)（与顺序查找效率相同）；
一般情况：树结构介于平衡与单链表之间，时间复杂度接近O(log₂n)，但稳定性差。

（5）存在问题

​ 二叉排序树的核心缺陷是结构稳定性差：当插入序列有序或接近有序时，树会退化为单链表，导致查找效率急剧下降（从O(log₂n)降至O(n)）。为解决此问题，需引入 “平衡二叉树”。

7.3.2方法 2：平衡二叉树查找（Balanced Binary Tree, AVL 树）

（1）前提条件：平衡二叉树的定义

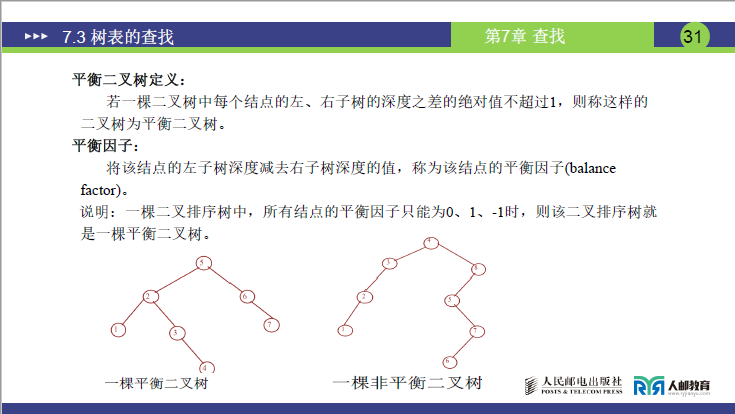
平衡二叉树定义：若一棵二叉树中每个结点的左、右子树的深度之差的绝对值不超过1，则称这样的二叉树为平衡二叉树。

平衡二叉树是 “满足平衡条件的二叉排序树”，核心指标是平衡因子：

• 平衡因子（Balance Factor, BF）：节点左子树深度 - 右子树深度；
• 平衡条件：所有节点的平衡因子只能为-1、0、1（左、右子树深度差≤1）。

“一棵平衡二叉树” 与 “一棵非平衡二叉树” 对比：

• 平衡二叉树：根节点 BF=0（左深 2，右深 2），所有子节点 BF∈{-1,0,1}；
• 非平衡二叉树：节点 5，BF=-2（左深 0，右深 2），违反平衡条件。

（2）核心思想（查找 + 平衡调整）

​ 若平衡二叉树为空，则查找失败，否则，先拿根结点值与待查值进行比较，若相等，则查找成功，若根结点值大于待查值，则进入左子树重复此步骤，否则，进入右子树重复此步骤，若在查找过程中遇到平衡二叉树的叶子结点时，还没有找到待找结点，则查找不成功。

平衡二叉树的查找逻辑与二叉排序树完全相同（“比根大找右，比根小找左”），差异在于：

• 插入新节点后，需检查树的平衡性：若出现 “不平衡节点”（BF=±2），则通过旋转调整恢复平衡；
• 调整原则：找到 “与插入点最近的不平衡节点”（从插入点向上回溯第一个 BF=±2 的节点），仅调整该节点及其子树（局部调整，避免全树重构）。

平衡二叉树查找步骤：

• 第一步：调整成一棵平衡二叉排序树
• 第二步：平衡二叉树查找

（3）四大平衡调整场景（插入导致不平衡的解决）

第一步：非平衡二叉树的平衡处理

若一棵二叉排序树是平衡二叉树，扦入某个结点后，可能会变成非平衡二叉树，这时，就可以对该二叉树进行平衡处理，使其变成一棵平衡二叉树。
处理的原则应该是处理与扦入点最近的、而平衡因子又比1大或比-1小的结点。下面将分四种情况讨论平衡处理。

插入新节点后，不平衡节点的 BF 可能为2（左子树过深）或-2（右子树过深），对应 4 种调整类型：

①LL 型调整（左左型：左子树的左子树插入）

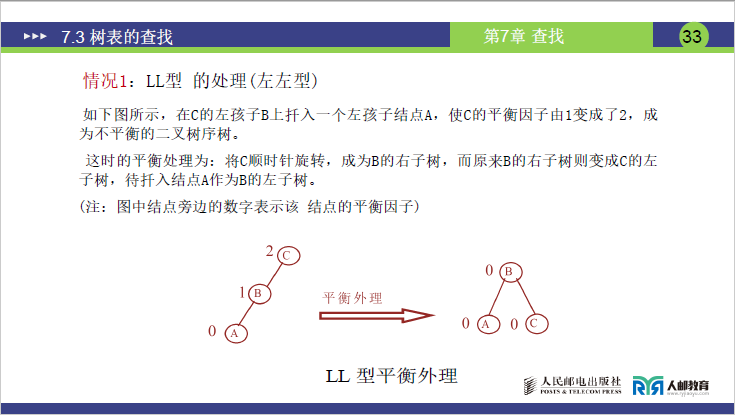
• 场景：不平衡节点 A 的 BF=2，且 A 的左孩子 B 的 BF=1（B 的左子树插入新节点，导致 A 左子树过深）；
• 调整步骤：顺时针旋转 A 节点（以 B 为轴）：
  1. 将 B 的右子树（若存在）作为 A 的左子树；
  2. 将 A 作为 B 的右子树；
  3. 更新 B 为新的根节点（原 A 的父节点指向 B）。
• 示例：C（BF=2）的左孩子 B（BF=1）的左子树插入 A → 顺时针旋转 C，B 成为新根，原 B 的右子树变为 C 的左子树，C 变为 B 的右子树。

如下图所示，在C的左孩子B上扦入一个左孩子结点A，使C的平衡因子由1变成了2，成为不平衡的二叉树序树。
这时的平衡处理为：将C顺时针旋转，成为B的右子树，待扦入结点A作为B的左子树。
(注：图中结点旁边的数字表示该结点的平衡因子)

②LR 型调整（左右型：左子树的右子树插入）

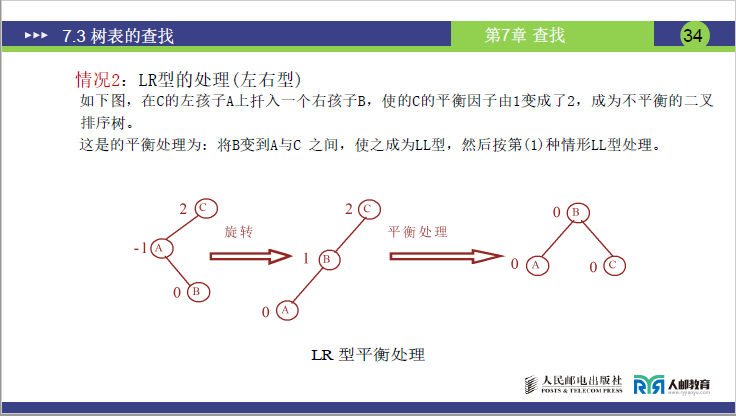
• 场景：不平衡节点 A 的 BF=2，且 A 的左孩子 B 的 BF=-1（B 的右子树插入新节点，导致 A 左子树过深）；
• 调整步骤：先左旋 B，再右旋 A（两次旋转）：
  1. 以 B 的右孩子 C 为轴，逆时针旋转 B：将 C 的左子树作为 B 的右子树，B 作为 C 的左子树；
  2. 以 C 为轴，顺时针旋转 A：将 C 的右子树作为 A 的左子树，A 作为 C 的右子树；
  3. 更新 C 为新的根节点。
• 示例（课件）：C（BF=2）的左孩子 A（BF=-1）的右子树插入 B → 先左旋 A（B 成为 A 的父节点），再右旋 C（B 成为新根）。

如下图，在C的左孩子A上扦入一个右孩子B，使的C的平衡因子由1变成了2，成为不平衡的二叉排序树。
这是的平衡处理为：将B变到A与C 之间，使之成为LL型，然后按第(1)种情形LL型处理。

③RR 型调整（右右型：右子树的右子树插入）

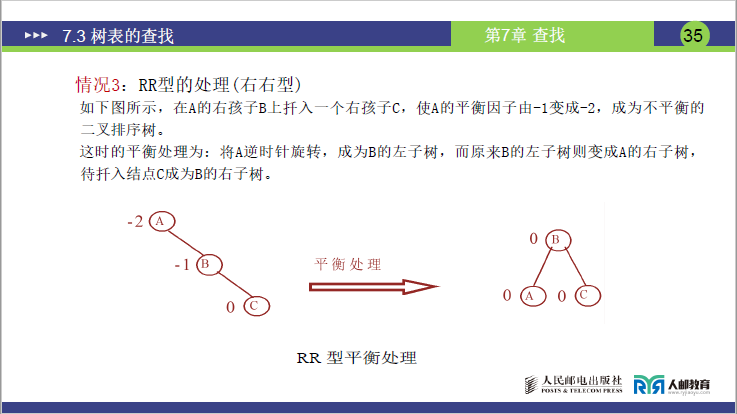
• 场景：不平衡节点 A 的 BF=-2，且 A 的右孩子 B 的 BF=-1（B 的右子树插入新节点，导致 A 右子树过深）；
• 调整步骤：逆时针旋转 A 节点（以 B 为轴）：
  1. 将 B 的左子树（若存在）作为 A 的右子树；
  2. 将 A 作为 B 的左子树；
  3. 更新 B 为新的根节点。
• 示例（课件）：A（BF=-2）的右孩子 B（BF=-1）的右子树插入 C → 逆时针旋转 A，B 成为新根，原 B 的左子树变为 A 的右子树，A 变为 B 的左子树。

如下图所示，在A的右孩子B上扦入一个右孩子C，使A的平衡因子由-1变成-2，成为不平衡的二叉排序树。
这时的平衡处理为：将A逆时针旋转，成为B的左子树，而原来B的左子树则变成A的右子树，待扦入结点C成为B的右子树。

④RL 型调整（右左型：右子树的左子树插入）

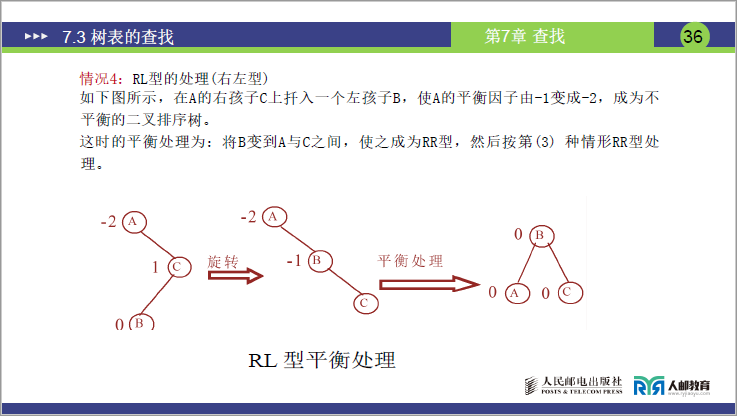
• 场景：不平衡节点 A 的 BF=-2，且 A 的右孩子 B 的 BF=1（B 的左子树插入新节点，导致 A 右子树过深）；
• 调整步骤：先右旋 B，再左旋 A（两次旋转）：
  1. 以 B 的左孩子 C 为轴，顺时针旋转 B：将 C 的右子树作为 B 的左子树，B 作为 C 的右子树；
  2. 以 C 为轴，逆时针旋转 A：将 C 的左子树作为 A 的右子树，A 作为 C 的左子树；
  3. 更新 C 为新的根节点。
• 示例（课件）：A（BF=-2）的右孩子 C（BF=1）的左子树插入 B → 先右旋 C（B 成为 C 的父节点），再左旋 A（B 成为新根）。

如下图所示，在A的右孩子C上扦入一个左孩子B，使A的平衡因子由-1变成-2，成为不平衡的二叉排序树。
这时的平衡处理为：将B变到A与C之间，使之成为RR型，然后按第(3) 种情形RR型处理。

（4）平衡二叉树的构建示例（课件关键字序列4,5,7,2,1,3,6）

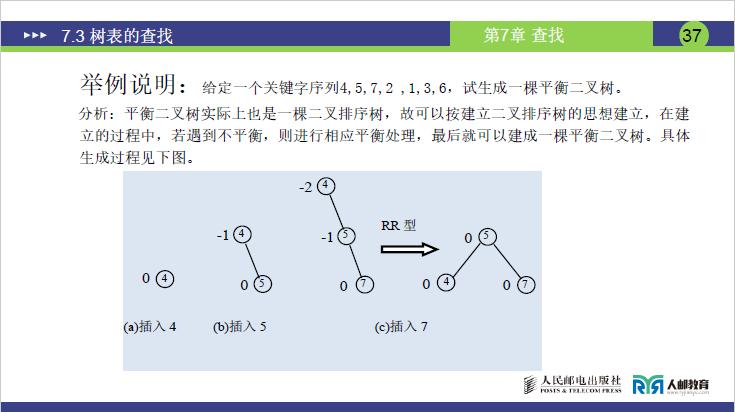
举例说明：给定一个关键字序列4,5,7,2 ,1,3,6，试生成一棵平衡二叉树。
分析：平衡二叉树实际上也是一棵二叉排序树，故可以按建立二叉排序树的思想建立，在建立的过程中，若遇到不平衡，则进行相应平衡处理，最后就可以建成一棵平衡二叉树。具体生成过程见下图。

给定一个关键字序列4,5,7,2 ,1,3,6，试生成一棵平衡二叉树。

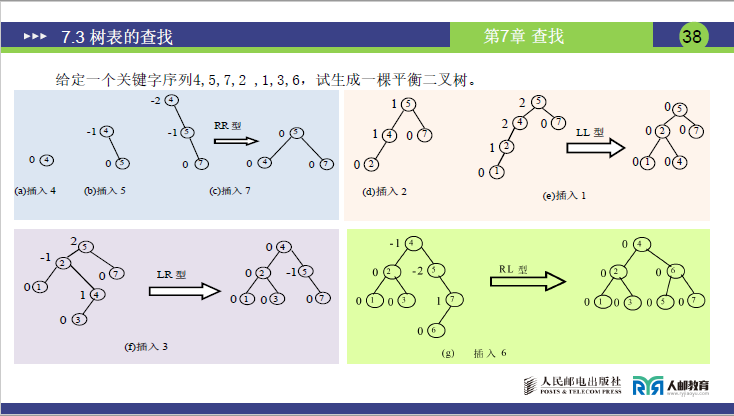
插入顺序	插入后状态	平衡调整	最终树结构（核心节点）
1. 插入 4	根：4（BF=0）	无（平衡）	4（无左右子树）
2. 插入 5	5>4 → 4 右子树（4 的 BF=-1，5 的 BF=0）	无（平衡）	4 右孩子：5
3. 插入 7	7>4→右子树，7>5→5 右子树 → 4 的 BF=-2（不平衡，RR 型）	RR 调整：以 5 为轴逆时针旋转 4 → 5 成为根，4 为 5 左子树，7 为 5 右子树	根：5（左：4，右：7）
4. 插入 2	2<5→左子树，2<4→4 左子树 → 5 的 BF=1，4 的 BF=1（平衡）	无	4 左孩子：2
5. 插入 1	1<5→左子树，1<4→左子树，1<2→2 左子树 → 4 的 BF=2（不平衡，LL 型）	LL 调整：以 2 为轴顺时针旋转 4 → 2 成为 4 的父节点，1 为 2 左子树，4 为 2 右子树；5 的 BF=0（平衡）	5 左孩子：2（左：1，右：4）
6. 插入 3	3<5→左子树，3>2→右子树，3<4→4 左子树 → 2 的 BF=-1，4 的 BF=1（2 的 BF=2，不平衡，LR 型）	LR 调整：先以 3 为轴左旋 4（3 成为 4 的父节点），再以 3 为轴右旋 2（3 成为 2 的父节点） → 5 的左孩子变为 3	5 左孩子：3（左：2，右：4）；2 左孩子：1
7. 插入 6	6<5→右子树，6<7→7 左子树 → 5 的 BF=-1，7 的 BF=1（平衡）	无	7 左孩子：6

（5）平衡二叉树的查找与性能对比

​ 平衡二叉树本身就是一棵二叉排序树，故它的查找与二叉排序树完全相同。但它的查找性能优于二叉排序树，不像二叉排序树一样，会出现最坏的时间复杂度O(n)，它的时间复杂度与二叉排序树的最好时间复杂相同，都为O(log₂n)。

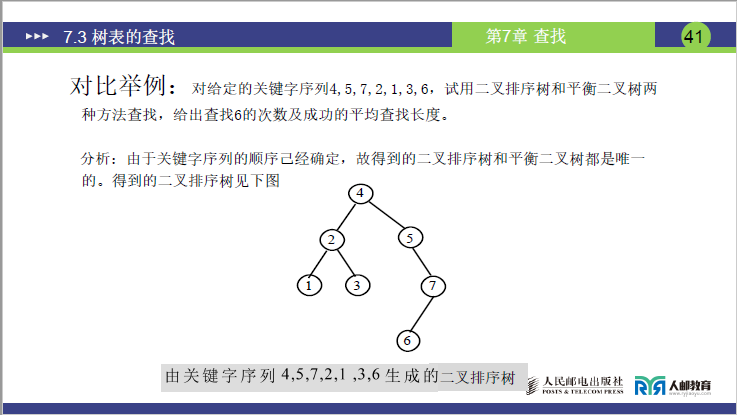
对比举例：对给定的关键字序列4、5、7、2、1、3、6，试用二叉排序树和平衡二叉树两种方法查找，给出查找6的次数及成功的平均查找长度。
分析：由于关键字序列的顺序己经确定，故得到的二叉排序树和平衡二叉树都是唯一的。得到的二叉排序树见下图：

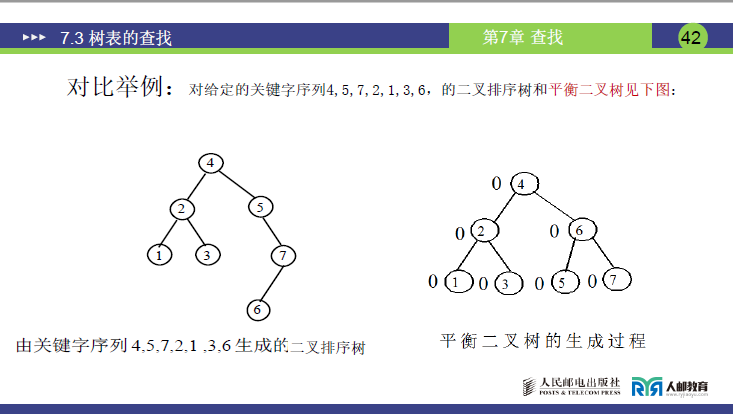
①查找逻辑（与二叉排序树一致）

• 若树空→查找失败；
• 若待查关键字 = 根→成功；
• 若待查关键字＜根→递归查左子树；
• 若待查关键字＞根→递归查右子树。

②性能对比

以关键字序列「4,5,7,2,1,3,6」为例，对比二叉排序树与平衡二叉树：

指标	二叉排序树	平衡二叉树
查找「6」的次数	4 次（深度 4 层）	2 次（深度 2 层）
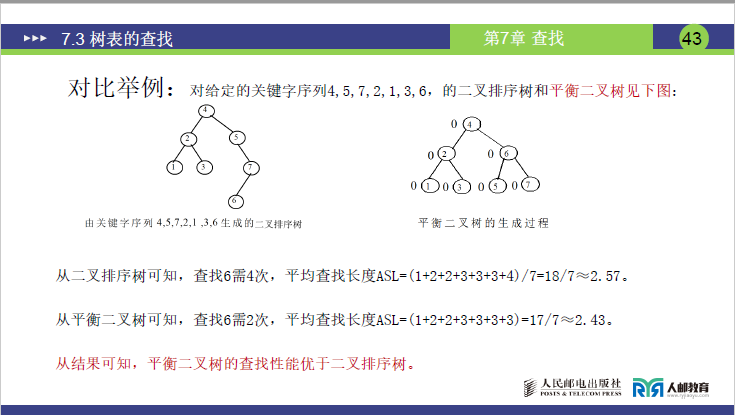
成功平均查找长度（ASL）	(1+2+2+3+3+3+4)/7≈2.57	(1+2+2+3+3+3+3)/7≈2.43
时间复杂度	最坏 O (n)（退化时）	稳定 O (log₂n)

• 结论：平衡二叉树通过 “边构建边调整”，避免了二叉排序树的退化风险，查找性能更优且稳定。

③平衡二叉树的查找及性能分析

​ 平衡二叉树本身就是一棵二叉排序树，故它的查找与二叉排序树完全相同。但它的查找性能优于二叉排序树，不像二叉排序树一样，会出现最坏的时间复杂度O(n)，它的时间复杂度与二叉排序树的最好时间复杂相同，都为O(log₂n)。

7.3.3 B - 树（平衡多路查找树）

（1）核心定义

• 本质：适用于外存（如硬盘） 的平衡多路查找树（解决二叉树 “层深过大、IO 次数多” 的问题）。
• 一棵m阶的B-树或为空树，或为满足下列特性的m叉树：：
  1. 树中每个节点至多有m棵子树；
  2. 若根结点不是叶子结点，则至少有两棵子树；
  3. 除根结点之外的所有非终端结点至少有m/2棵子树；
  4. 所有的非终端结点中包含下列信息数据(n,A₀,K₁,A₁,K₂,A₂,…,K_n,A_n)其中K_i(i=1,…,n)为关键字，且K_i<K_i+1,(i=1,…,n-1)为关键字，且K_i<K_i+1,(i=1,…,n-1)
     • n：节点的关键字个数（满足⌈m/2⌉-1 ≤ n ≤ m-1）；
     • K₁＜K₂＜...＜Kₙ：有序关键字；
     • A₀~Aₙ：指针（A₀指向比 K₁小的子树，A₁指向比 K₁大且比 K₂小的子树，…，Aₙ指向比 Kₙ大的子树）；
     • 关键关系：指针数 = 关键字数 + 1（老师强调 “N 个关键字对应 N+1 个方向”）；
  5. 所有叶子节点在同一层（叶子是空指针，不存储数据，课件 46 页示例中省略不画）。

实例解读：B-树是一种平衡的多路查找树

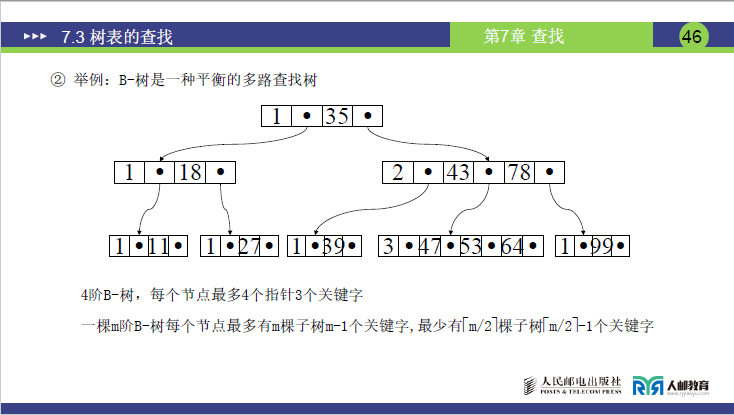
• 阶 m=4→最多 4 棵子树、3 个关键字；非根非终端节点至少⌈4/2⌉=2 棵子树、1 个关键字。
• 一棵m阶B-树每个节点最多有m棵子树m-1个关键字,最少有⌈m/2⌉棵子树⌈m/2⌉-1个关键字
• 根节点：关键字 35，指针 A₀（指向比 35 小的子树）、A₁（指向比 35 大的子树）→符合 “根非叶子时至少 2 棵子树”；
• 下层节点：如含关键字 18、43、78 的节点，有 4 个指针（A₀~A₃）→最多 4 棵子树，符合 m=4 的限制。

（2）B - 树的核心操作

①插入操作

插入方法：
B-树「m/2⌉-1≤节点中的关键字个数≤ m-1,并且整个B-树可以看成全部由关键字组成的树，每次插入一个关键字不是在树中添加一个叶子节点，而是在查找的过程中找到叶子节点所在层的上一层（叶子节点是记录，上一层是关键字最后一层），在某个节点中添加一个关键字，若结点的关键字个数不超过m-1，则插入完成，否则产生节点的分裂。

• 核心原则：插入仅在 “叶子节点的上一层”（非叶子层）进行，若节点关键字数超 m-1→分裂节点（中间关键字上移为父节点的关键字）。
• 实战示例：3 阶 B - 树（又称 2-3 树，m=3，最多 2 个关键字、3 棵子树；最少 1 个关键字、2 棵子树）插入「30,26,85,7」。

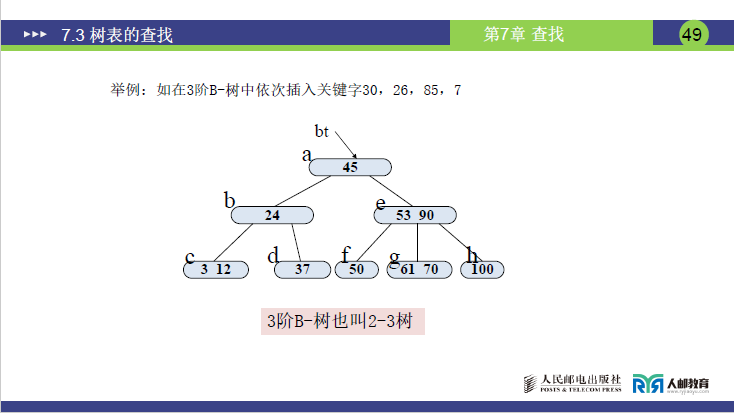
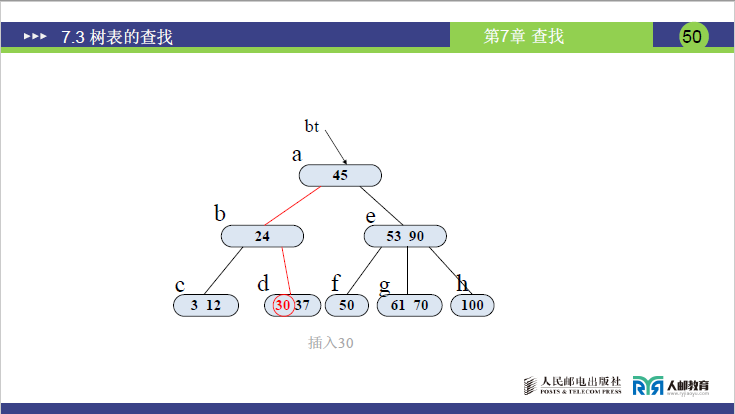
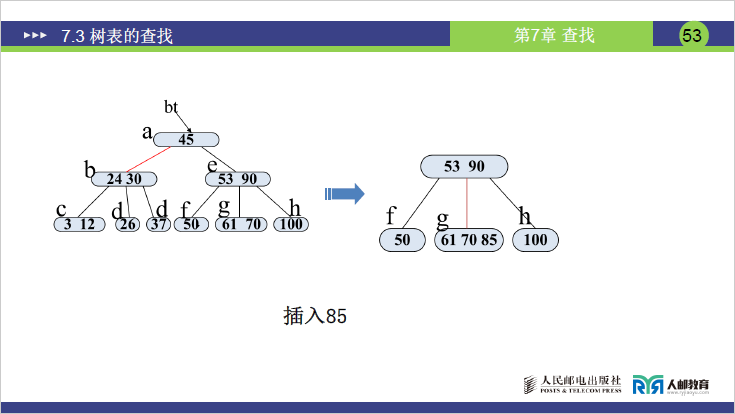
步骤 1：插入 30

• 原树：根 a (45)，左子树 b (24)，右子树 e (53,90)，b 的子树 c (3,12)、d (37)。
• 30 的哈希地址：比 24 大、比 37 小→插入 d 节点（d 原为 (37)，插入后为 (30,37)，关键字数 = 2≤m-1=2→无需分裂）。

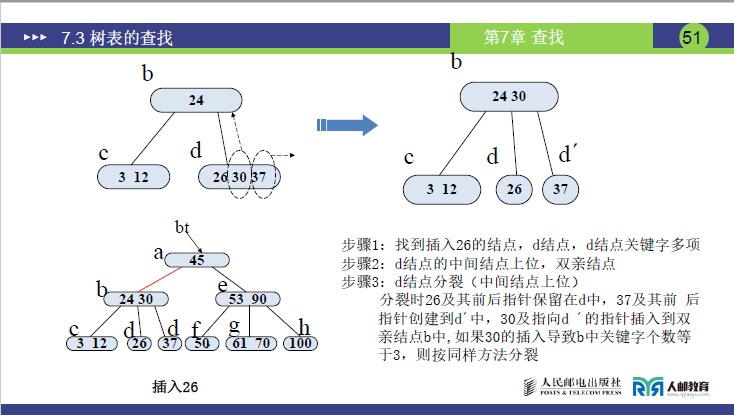
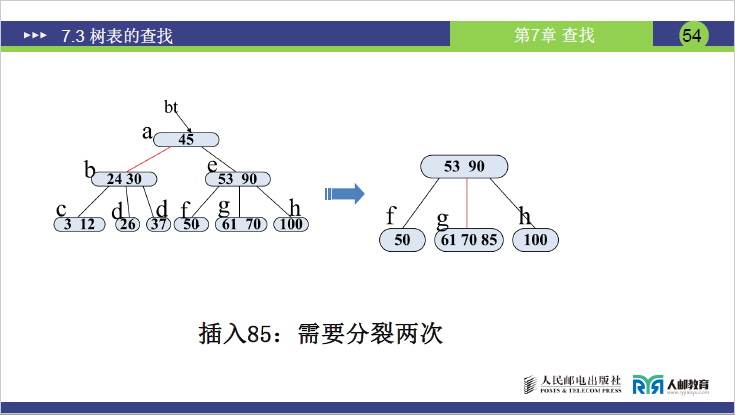
步骤 2：插入 26

• 26 比 24 大、比 30 小→插入 d 节点（d 变为 (26,30,37)，关键字数 = 3＞2→分裂）。
• 分裂规则（老师强调）：
  1. 取中间关键字 30 上移至父节点 b（b 原为 (24)，变为 (24,30)）；
  2. d 分裂为 d₁(26)、d₂(37)，d₁作为 24 的右子树，d₂作为 30 的右子树。

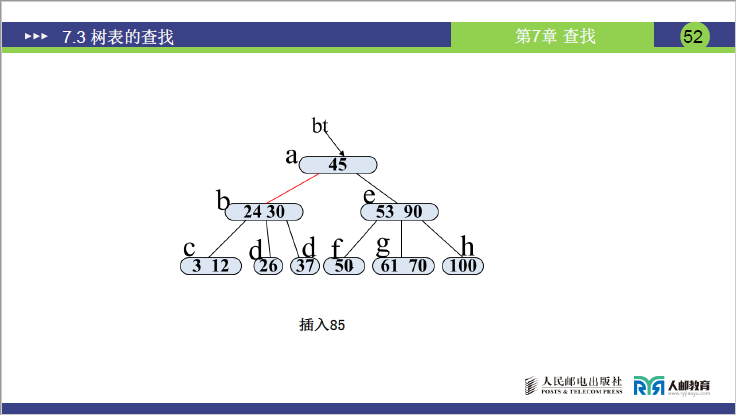
步骤 3：插入 85

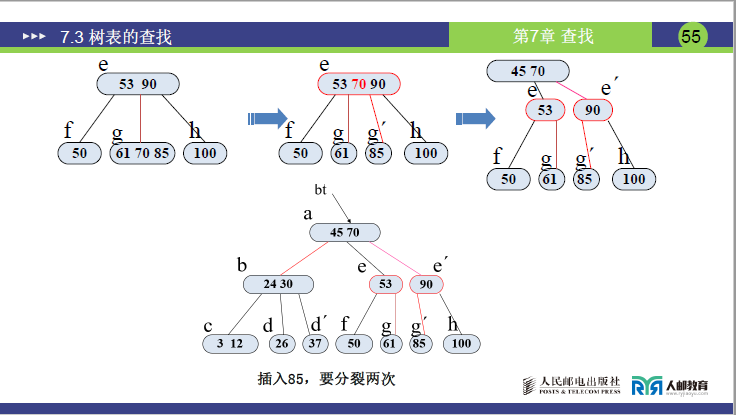
• 85 比 45 大、比 53 大、比 90 小→插入 e 的子树 g (61,70)（g 变为 (61,70,85)，关键字数 = 3＞2→分裂）。
• 分裂 1：中间关键字 70 上移至 e（e 原为 (53,90)，变为 (53,70,90)，关键字数 = 3＞2→再次分裂）；
• 分裂 2：中间关键字 70 上移至根 a（a 原为 (45)，变为 (45,70)）；
• e 分裂为 e₁(53)、e₂(90)，g 分裂为 g₁(61)、g₂(85)。

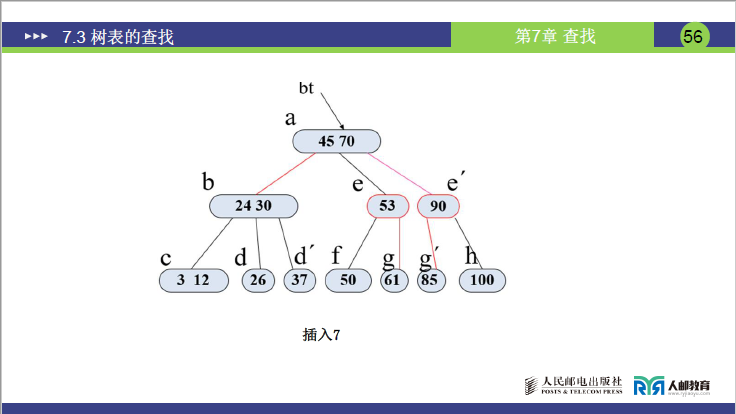
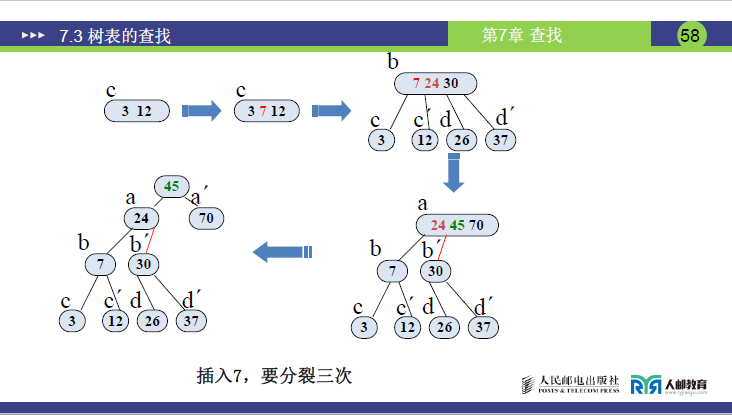
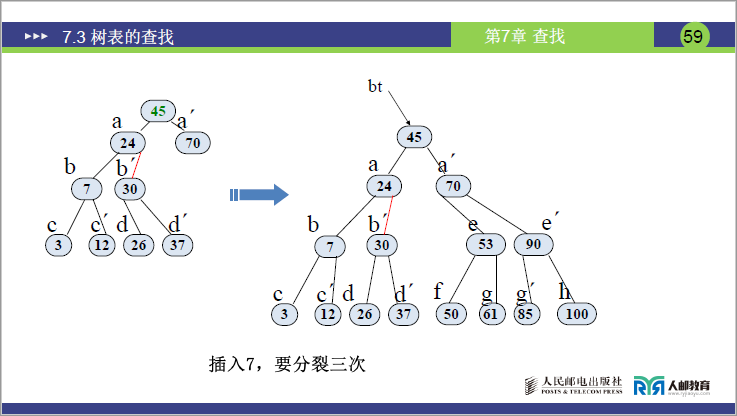
步骤 4：插入 7

• 7 比 24 小、比 3 大、比 12 小→插入 c 节点（c 原为 (3,12)，插入后为 (3,7,12)，关键字数 = 3＞2→分裂）。
• 分裂 1：中间关键字 7 上移至 b（b 原为 (24,30)，变为 (7,24,30)，关键字数 = 3＞2→分裂）；
• 分裂 2：中间关键字 24 上移至根 a（a 原为 (45,70)，变为 (24,45,70)，关键字数 = 3＞2→分裂）；
• 分裂 3：中间关键字 45 上移为新根，a 分裂为 a₁(24)、a₂(70)→最终树平衡。
• 插入总结：分裂可能 “自下向上层层传递”，最终保证树的平衡（所有叶子在同一层）。

②删除操作

• 核心原则：删除优先在 “最下层非叶子节点” 进行，删除后若关键字数＜⌈m/2⌉-1→通过 “借关键字” 或 “合并节点” 恢复平衡。
• 3 阶 B - 树删除示例：原树含关键字「45,24,53,90,37,50,61,70,3,12,100」，删除「12,50,53,37」。

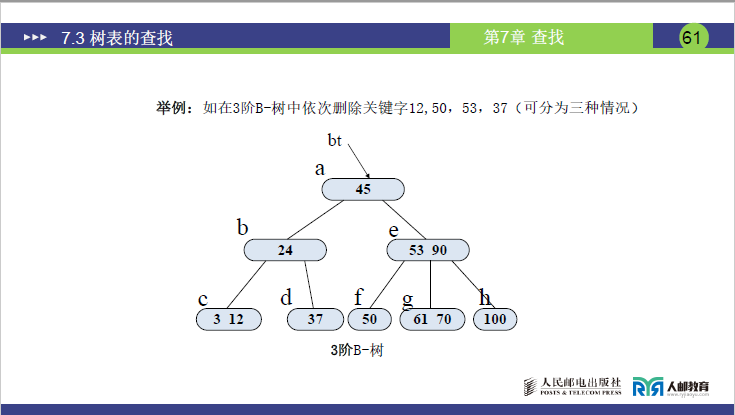
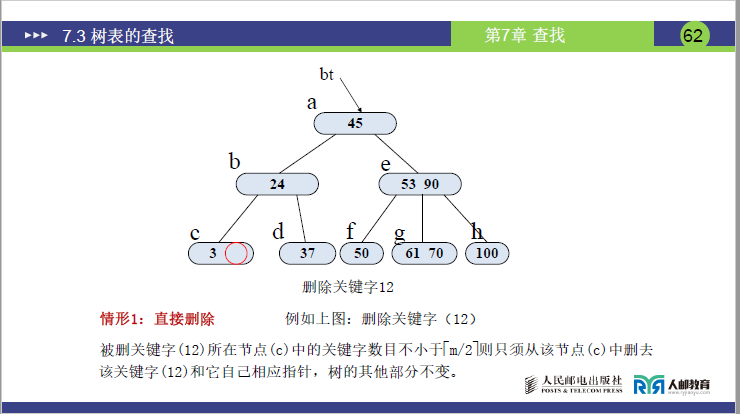
情况 1：直接删除（关键字所在节点数≥⌈m/2⌉）

• 删除 12：12 在 c 节点 (3,12)，删除后 c 节点关键字数 = 1（≥⌈3/2⌉-1=1）→直接删，树不变。

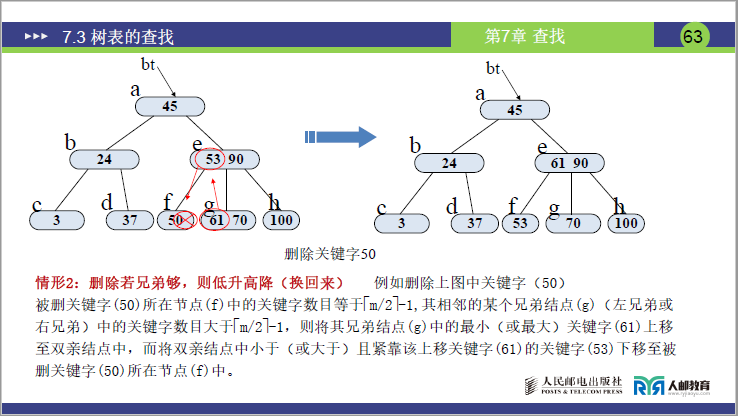
情况 2：兄弟 “够借”（兄弟节点数＞⌈m/2⌉-1）

• 删除 50：50 在 f 节点 (50)，删除后 f 节点数 = 0（＜1）；
• 右兄弟 g 节点 (61,70) 数 = 2（＞1）→借 g 的最小关键字 61 上移至父节点 e (53,90)，父节点的 53 下移至 f→e 变为 (53,61,90)，f 变为 (53)，g 变为 (70)。

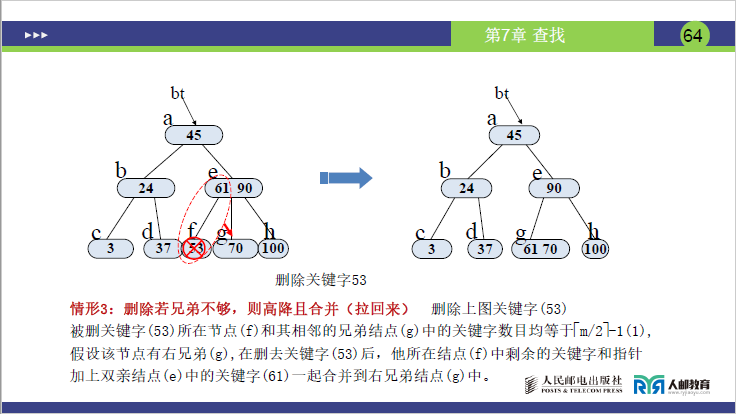
情况 3：兄弟 “不够借”（兄弟节点数 =⌈m/2⌉-1）→合并节点

• 删除 53：53 在 f 节点 (53)，删除后 f 数 = 0；右兄弟 g 节点 (70) 数 = 1（=1）；
• 合并规则：将父节点 e 的 61 下移，与 f、g 合并为 (61,70)→e 变为 (90)，树平衡。

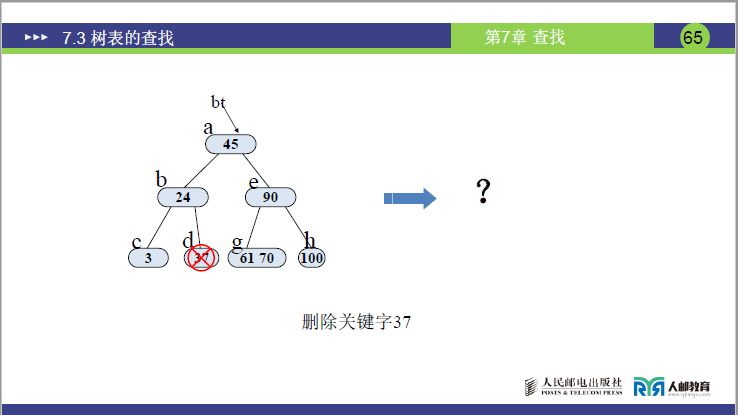
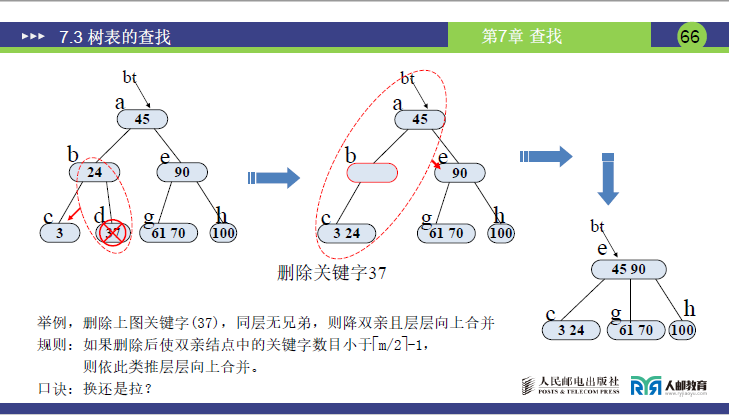
情况 4：合并传递至根

• 删除 37：37 在 d 节点 (37)，删除后 d 数 = 0；无兄弟→合并父节点 b (24) 与根 a (45,90)→最终树简化为根 (24,45,90)，子树 c (3)、g (61,70)、h (100)。

（3）B - 树的查找性能

• 逻辑：从根出发，比较关键字确定待查区间（通过 A₀~Aₙ指针），直至叶子层（空指针→失败）或找到关键字→成功。
• 性能优势：多路结构减少 “层深”，外存 IO 次数仅为树的深度（如 m=100 的 B - 树，100 万数据仅需 3 层，IO 仅 3 次）。

7.3.4 B + 树（B - 树的变型）

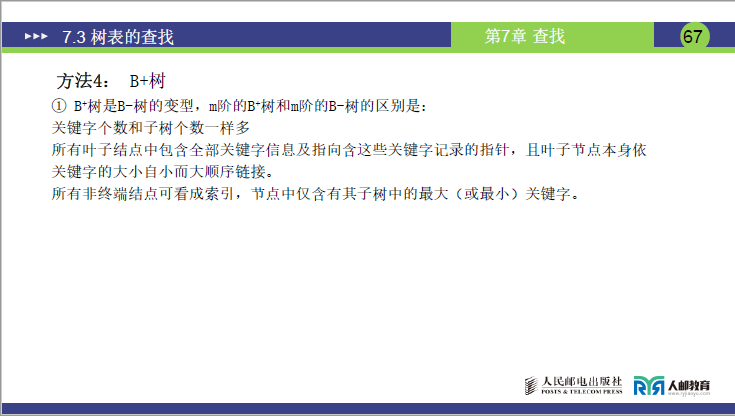
（1）B + 树与 B - 树的核心区别

对比维度	B - 树	B + 树
关键字与子树数关系	子树数 = 关键字数 + 1	子树数 = 关键字数（讲课强调 “个数一样多”）
关键字存储	非终端节点存储部分关键字，叶子无关键字	所有关键字存储在叶子节点（完整集合），非终端仅存 “索引关键字”（子树最大 / 最小关键字）
叶子节点特性	叶子为无信息空指针，不链接	叶子节点按关键字有序链接（支持顺序查找，讲课重点）
查找终止位置	找到关键字即可终止（非终端 / 叶子层均可）	必须到叶子节点（无论成功与否，课件 P68）

（2）B + 树的查找、插入与删除

1. 查找：与 B - 树类似，沿索引逐层向下，最终到叶子节点确认是否存在（支持 “随机查找”+“顺序查找”，因叶子有序链接）；
2. 插入：仅在叶子节点插入，若叶子关键字数超 m，分裂为两个叶子（关键字数分别为⌊(m+1)/2⌋和⌈(m+1)/2⌉），中间关键字插入双亲（非终端仅存索引）；
3. 删除：仅删除叶子节点关键字，若叶子关键字数低于⌈m/2⌉，与兄弟合并（规则同 B - 树）；非终端的 “索引关键字” 可保留（即使对应叶子关键字被删，仍作为分界索引）。

讲课补充：B + 树重点是 “叶子存全量关键字 + 有序链接”，适合数据库索引（需范围查询），B - 树适合文件系统，本节课核心掌握 B - 树，B + 树了解即可。

7.3.5 树表查找方法对比与总结

查找方法	结构特点	查找性能（时间复杂度）	适用场景	核心优势 / 不足
二叉排序树	二叉，动态	最好 O (log₂n)，最坏 O (n)	内存中简单动态查找	实现简单，性能不稳定（易退化）
平衡二叉树	二叉，平衡（深度差≤1）	稳定 O (log₂n)	内存中高效动态查找	性能稳定，仍为二叉（深度较大）
B - 树（多路）	多路，平衡	稳定 O (logₘn)（m 为路数）	外存查找（数据库、文件）	多路减少深度，降低 IO 成本
B + 树（B - 树变型）	多路，叶子有序	稳定 O (logₘn)	数据库索引（范围查询）	支持顺序查找，全量关键字在叶子

总结（讲课提炼）：

树表查找的核心是 “动态调整 + 平衡”：二叉排序树是基础，平衡二叉树解决其退化问题，B - 树通过 “多路” 进一步优化外存性能；B + 树则针对 “顺序查找” 需求优化，需根据实际存储场景（内存 / 外存、是否需范围查询）选择。

7.3.6 关键公式与术语整理（核心）

1. B - 树节点关键字数范围：⌈m/2⌉-1 ≤ n ≤ m-1（m 为阶数）；
2. 三阶 B - 树（2-3 树）：m=3，n≥1，n≤2；
3. 装填因子（散列表相关，对比参考）：α=n/m（n 为元素数，m 为表长），B - 树无装填因子，靠节点分裂 / 合并保证平衡；
4. 平衡因子（平衡二叉树相关，对比参考）：左子树深度 - 右子树深度（仅 - 1,0,1），B - 树靠 “所有叶子同层” 保证平衡，无需平衡因子。

7.4 散列表的查找

7.4.1知识点1

（1）本节课概述

本节课聚焦散列查找（又称哈希查找）的基础部分，是考研高频考点。核心目标是理解 “如何通过函数直接计算关键字存储地址，避免大量无效比较”，主要覆盖两部分内容：

1. 散列查找的基本概念（术语、冲突原因、学习重点）；
2. Hash 函数的构造原则与 6 种常用构造方法（重点为除留余数法）。

（2）散列查找基本概念

散列查找的核心优势是不通过大量无效比较，直接通过函数计算关键字的存储地址，这与顺序查找（逐一遍历）、二分查找（判定树比较）、树表查找（树深度比较）有本质区别。

①核心术语

术语	定义	解释	补充说明
散列 / 哈希	在存放记录时，通过相同函数计算存储位置，并按此位置存放，这种方法称为Hash方法。	两种等价叫法，均指 “通过函数计算关键字存储地址” 的查找思想	英文均为 Hash，后续笔记中 “散列” 与 “哈希” 通用
哈希方法	是指在Hash方法中使用的函数。	核心逻辑：用哈希函数将关键字映射为存储地址，再用地址直接访问数据的方法	是散列查找的 “方法论”，涵盖 “存储” 与 “查找” 两个过程（边存边查）
哈希函数（H）	按Hash方法构造出来的表称为Hash表	输入为关键字（K），输出为存储地址（ADD）的函数，记为 ADD = H(K)	函数设计直接决定查找效率，理想状态下不同 K 对应不同 ADD（无冲突）
哈希表	通过Hash函数计算记录的存储位置，我们把这个存储位置称为Hash地址。	按哈希函数计算的地址，有序存储关键字的表结构（本质是顺序表的特殊应用）	表的大小记为 M（申请的存储单元总数），需提前确定
哈希冲突	不同记录的关键字经过Hash函数的计算可能得到同一Hash地址，即key1≠key2时，H(key1)＝H(key2)。这种现象叫做“冲突”	两个不同关键字代入哈希函数后，得到相同地址的现象	例：K1=18、K2=31，若 H (K)=K%13，则 H (18)=5、H (31)=5，二者冲突

②冲突的产生与影响因素

通过 “房间跑步” 类比（空间越小越易碰撞），总结冲突的 3 个核心影响因素：

1. Hash 函数的优劣
   • 若 Hash 函数能让关键字地址 “均匀分布”，冲突概率低；若函数设计差（如H(key)=1，所有关键字地址都是 1），冲突会频繁发生。
2. 装填因子 α（Alpha）
   • 定义（课件 76 页）：散列表中已存元素个数n与散列表大小m的比值，即α = n/m。
   • 讲课分析：
     • α 越小：空间越充裕，冲突概率越低（如m=100、n=10，α=0.1，几乎无冲突）；
     • α 越大：空间越拥挤，冲突概率越高（如m=10、n=9，α=0.9，极易冲突）；
     • 实际取值（讲课补充）：需平衡 “空间利用率” 与 “冲突概率”，一般 α 取 60%-70%。
3. 解决冲突的方法
   • 即使 Hash 函数和 α 合理，仍可能冲突，需依赖有效的冲突解决方法（如线性探查、链地址法，下节课重点讲解）。

③散列查找的学习重点

讲课明确 3 个核心知识点，是后续学习的核心框架：

1. Hash 函数构造：设计 “计算简单、地址分布均匀” 的函数，减少冲突；
2. 冲突解决方案：制定冲突发生后的处理规则；
3. 散列查找性能分析：通过平均查找长度（ASL）评估查找效率。

④实例：散列表构建与查找

已知条件

• 关键字序列：18、75、60、43、54、90、46；
• Hash 函数：H(key)=key%13；
• 散列表大小：地址 0-15（共 16 个存储单元）。

步骤 1：计算每个关键字的 Hash 地址

• H(18)=18%13=5
• H(75)=75%13=10
• H(60)=60%13=8（13×4=52，60-52=8）
• H(43)=43%13=4（13×3=39，43-39=4）
• H(54)=54%13=2（13×4=52，54-52=2）
• H(90)=90%13=12（13×6=78，90-78=12）
• H(46)=46%13=7（13×3=39，46-39=7）

步骤 2：构建散列表

地址	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
关键字	-	-	54	-	43	18	-	46	60	-	75	-	90	-	-	-

步骤 3：查找示例

• 计算 Hash 地址：H(75)=75%13=10；
• 直接访问HT[10]，找到 75；
• 特点（讲课强调）：无需任何比较，直接通过地址查找，效率极高（理论时间复杂度 O (1)）。

（3）Hash 函数构造

Hash 函数是散列查找的 “核心引擎”，构造时需兼顾 “计算效率” 与 “地址均匀性”。

①Hash 函数构造的关键要求

需考虑 5 个因素，直接影响函数优劣：

1. 计算 Hash 函数的时间：尽量简单（如取余、线性运算），避免复杂计算（如高次幂）；
2. 关键字的长度：若关键字过长（如 10 位数字），需简化（如取后几位）；
3. Hash 表的大小：函数值需在 Hash 表地址范围内（如地址 0-15，函数值不能超过 15）；
4. 关键字的分布情况：若关键字集中在某一区间，需通过函数 “离散化”（如除留余数法）；
5. 记录的查找频率：查找频繁的关键字，尽量分配到易访问的地址（如地址中间区域）。

②常用 Hash 函数构造方法（6 种）

A.直接定址法

• 定义：取关键字的线性函数值作为 Hash 地址，公式为：H(key) = a×key + b

  （其中a、b为常数，通常a=1、b=0，即H(key)=key）。

• 特点：

  • 优点：一对一映射，无冲突，计算简单；
  • 缺点：Hash 地址空间需与关键字集合大小一致，若关键字范围大（如 1000-100000），会浪费大量空间（需申请 99001 个单元，但可能只存 10 个关键字）。

• 讲课补充：实际应用极少，仅适用于关键字范围小且连续的场景（如学生学号 1-50，直接用学号作为地址）。

B.除留余数法（重点！考研高频）

• 课件定义：用关键字对常数p取余，公式为：Hash(key)=key%p(p≤m)

  其中m为 Hash 表大小，p需取 “不大于m且接近m的质数”，或 “不含小于 20 的质因子的合数”，且p不靠近 2 的幂（如 8、16）。

• 讲课补充：p的 3 个核心取值规则（考研必背）：

  1. p≤m：若p>m，取余结果可能超出地址范围（如m=16，p=17，，虽合法但无意义）；
  2. p优先取质数：质数约数少，关键字余数更均匀（如p=13比p=12好，12 的约数多易导致地址聚集）；
  3. p不靠近 2 的幂：2 的幂的余数仅与关键字后几位相关，易冲突（如p=8，key=10（1010）、key=18（10010）均得余数 2）。

• 课件核心实例（与讲课一致，详细计算）：

  已知：关键字序列[18,75,60,43,54,90,46]，Hash 函数H(key)=key%13（p=13，m=16，地址范围 0~15）。

  步骤 1：逐个计算每个关键字的 Hash 地址：

  • H(18)=18%13=5（13×1=13，18-13=5）
  • H(75)=75%13=10（13×5=65，75-65=10）
  • H(60)=60%13=8（13×4=52，60-52=8）
  • H(43)=43%13=4（13×3=39，43-39=4）
  • H(54)=54%13=2（13×4=52，54-52=2）
  • H(90)=90%13=12（13×6=78，90-78=12）
  • H(46)=46%13=7（13×3=39，46-39=7）

  步骤 2：构建 Hash 表（一维数组HT）：

  Hash 地址	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
  关键字	-	-	54	-	43	18	-	46	60	-	75	-	90	-	-	-

  步骤 3：查找实例（查找k**ey=75）：

  • 计算地址：H(75)=75%13=10；
  • 直接访问HT[10]，找到 75；
  • 结果：0 次比较，体现散列查找的高效性（讲课强调：这是线性表、树表查找无法实现的）。

C.数字分析法

• 课件定义：针对 “n个d位关键字”，分析各位数字的分布频率，选取符号分布最均匀的若干位作为 Hash 地址。

• 课件核心公式（均匀度计算）：\(\lambda_k = \sum_{i=1}^{r} (a_{ik} - \frac{n}{r})^2\)

  其中：

  • a_ik：第k位上数字i的出现次数；
  • n：关键字总数；
  • r：数字范围（0~9 取 10）；
  • λ_k越小，第k位数字分布越均匀，越适合作为地址。

• 课件实例（详细计算均匀度）：

  已知：8 个 6 位关键字[942148,941269,940527,941630,941805,941558,942047,940001]，需选 1 位作为 Hash 地址。

  步骤 1：统计每一位数字的出现次数：

  • 第 1 位：均为 9（出现 8 次，其他数字 0 次）；
  • 第 2 位：均为 4（出现 8 次，其他数字 0 次）；
  • 第 3 位：0 出现 2 次、1 出现 4 次、2 出现 2 次（其他数字 0 次）；
  • 第 5 位：0 出现 2 次、2 出现 1 次、3 出现 1 次、4 出现 2 次、5 出现 1 次、6 出现 1 次（其他数字 0 次）。

  步骤 2：计算各位置的λ_k：

  • 第 1 位：λ1=(8−108)2×1+(0−108)2×9=(7.2)2+9×(0.8)2=51.84+5.76=57.6；
  • 第 3 位：λ3=(2−108)2×2+(4−108)2×1+(0−108)2×7=2×(1.2)2+(3.2)2+7×(0.8)2=2.88+10.24+4.48=17.6；
  • 第 5 位：λ5=(2−108)2×2+(1−108)2×4+(0−108)2×4=2×(1.2)2+4×(0.2)2+4×(0.8)2=2.88+0.16+2.56=5.6。

  步骤 3：选择地址位：

  因λ5最小（5.6），故选取第 5 位作为 Hash 地址（讲课补充：肉眼可观察第 5 位数字分散度最高，公式验证了这一结论）。

D.平方取中法

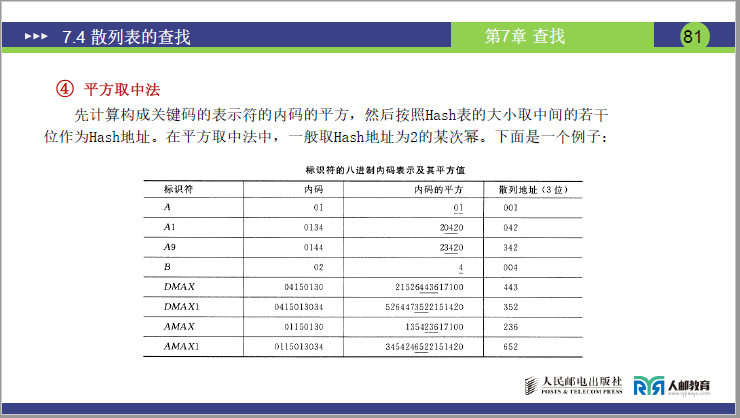
• 定义：先计算关键字的平方，再取平方值的 “中间几位” 作为 Hash 地址（适用于关键字位数较短且无明显分布规律的场景）。

• 原理（讲课补充）：关键字的平方值 “中间几位” 受关键字所有位影响，差异较大，能减少冲突（如 12 和 21，平方后为 144 和 441，中间位分别为 4 和 4，若关键字差异大，中间位差异也大）。

• 实例（课件 81 页 平方取中法示例表格）：

  标识符	八进制内码	内码的平方	散列地址（取中间 3 位）
  A	01	000001	001
  A1	0134	0020420	042
  A9	0144	0023420	342
  DMAX	04150130	21526443617100	443

  • 说明：Hash 地址通常取 2 的幂（如 3 位地址对应 8 位空间），中间位的选取需根据 Hash 表大小调整（如表大小 1000，取中间 3 位）。

E.折叠法

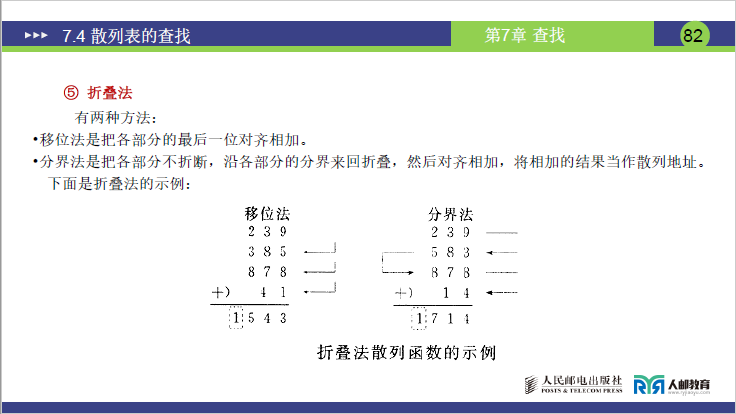
• 课件定义：将关键字拆分为若干等长片段，通过 “对齐相加” 合并片段作为 Hash 地址，分两种方式：

  1. 移位法：片段最后一位对齐，直接相加；
  2. 分界法：片段沿分界 “对折”（奇数片段中间不变），再相加。

• 课件实例（讲课补充计算步骤）：

  例 1：移位法（关键字key=123456，拆分为 3 位片段：12、34、56）：

  • 对齐方式：最后一位对齐（12→012，34→034，56→056）；
  • 相加：012+034+056=102；
  • Hash 地址 = 102。

  例 2：分界法（关键字key=1234567，拆分为 3 位片段：12、345、67）：

  • 对折方式：12 沿分界对折为 21，67 沿分界对折为 76，中间片段 345 不变；
  • 对齐相加：21+345+76=442；
  • Hash 地址 = 442（对折后片段更分散，进一步降低冲突率）。

F.随机数法

• 定义：取随机函数值作为 Hash 地址，公式为：Hash(key)=random(key)其中random为随机函数。

• 限制：仅适用于 “关键字长度不等且无规律” 的临时场景（如临时验证码）；

• 否定其通用性：工科需 “地址可追溯”，随机性无法重复定位（如再次查找同一关键字，随机地址可能变化），考研中极少考察。

本节课小结

1. 核心逻辑：散列查找通过 “Hash 函数计算地址” 实现高效查找，核心是 “减少冲突”；
2. 关键术语：Hash 方法、Hash 函数、Hash 表、Hash 地址、冲突（需理解冲突的 3 个影响因素）；
3. 重点方法：Hash 函数构造的 6 种方法中，除留余数法是考研核心（需掌握p的取值原则），数字分析法、平方取中法需理解原理；
4. 后续预告：下节课重点讲解 “冲突解决方案”（线性探查、链地址法等）及 “散列查找性能分析”。

（4）考研高频考点总结

1. Hash 函数构造（必考计算题）：
   • 除留余数法：p的 3 个取值规则（≤m、质数、不靠近 2 的幂）+ 地址计算实例（如课件 7 个关键字的 Hash 表构建）；
   • 数字分析法：均匀度公式λ**k的计算逻辑 + 地址位选择（课件 8 个 6 位关键字的实例）。
2. 术语定义（名词解释）：
   • 冲突：不同关键字得相同地址（例：K1=18、K2=31，H (K)=K%13=5）；
   • 装填因子α：公式α=m**n + 经验值 60%~70%。
3. 核心实例（必须掌握）：
   • 除留余数法的 Hash 表构建（7 个关键字，H (key)=key%13）；
   • 数字分析法的均匀度计算（8 个 6 位关键字选第 5 位作为地址）。

7.4.2 知识 2：处理冲突的方法（课件 84-91 页）

冲突是散列查找中不可避免的现象（不同关键字通过 Hash 函数得到同一地址，即key1\=key2但H(key1)=H(key2)）。课件及老师讲解中，核心处理方法分为 4 类，其中开放地址法和链地址法是考试与应用的重点。

（1）开放地址法（课件 84-85 页）

①定义

冲突发生时，生成一个探测序列，按序列探测 Hash 表中其他空闲存储单元，直到找到不冲突的单元为止。核心公式：Hi(key)=(H(key)+di)%m(i=1,2,…,m)

• H(key)：关键字的直接 Hash 地址；
• di：第i次探测的地址增量；
• m：Hash 表长度；
• 老师通俗解释：“像找空房子，若当前地址被占，就按规则往后 / 跳着找下一个空地址”。

②3 种地址增量

根据di的不同，开放地址法分为 3 类，前两类是考试重点：

类型	地址增量di规则	老师通俗解释	特点
线性探查再 Hash	di=1,2,…,m−1	“谦让往后找，每次多往后 1 个地址”	易产生 “淤积”（连续地址被占），但计算简单
二次探查再 Hash	di=±12,±22,…,±k2（k≤⌊m/2⌋）	“跳着找，先往后 1、再往前 1，再往后 4、往前 4”	淤积现象减轻，地址分布更均匀
伪随机探测再 Hash	di=伪随机函数值	“随机找空地址”	不易淤积，但增加随机数计算时间，应用少

（3）课件练习提示

已知 Hash 函数H(key)=key%7，Hash 表地址范围 0-6，关键字序列(25,6,42,11,15,31,14)，需分别用线性探查和二次探查解决冲突构造 Hash 表。

• 老师强调：Hash 表的结构由 3 个因素决定 ——Hash 函数、处理冲突方法、装填因子α（α=n/m，n为关键字个数，m为表长）。

（2）链地址法（拉链法）

①定义

将 Hash 地址相同的关键字，通过单链表链接起来；所有链表的表头结点组成一个向量（数组），向量长度与 Hash 地址范围一致。

• 老师解释：“同一‘房子’（Hash 地址）住不下，就在房子后面接‘小房间’（链表节点），表头存数组里”。

②详细例子

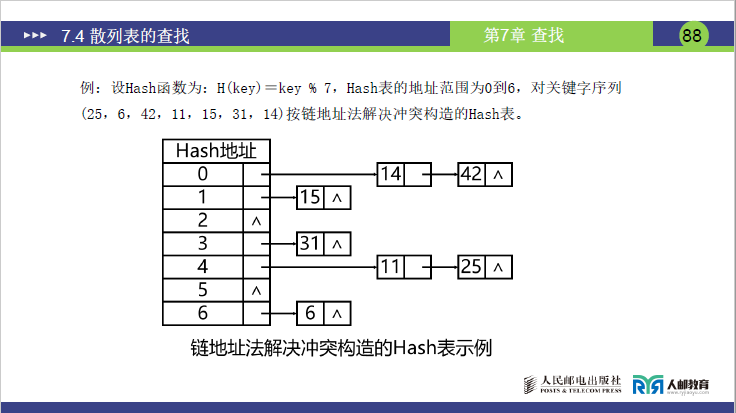
题目：Hash 函数H(key)=key%7，地址范围 0-6，关键字序列(25,6,42,11,15,31,14)，用链地址法构造 Hash 表。

步骤 1：计算每个关键字的 Hash 地址

• 25%7=4，6%7=6，42%7=0，11%7=4，15%7=1，31%7=3，14%7=0；
• 冲突关键字：42 与 14（地址 0）、25 与 11（地址 4）。

步骤 2：构建 Hash 表

Hash 表为长度 7 的数组，每个元素是链表表头，结构如下：

Hash 地址	链表结构（关键字链接）	查找次数说明
0	14 → 42	找 14 需 1 次，找 42 需 2 次
1	15	找 15 需 1 次
2	空（无关键字）	-
3	31	找 31 需 1 次
4	25 → 11	找 25 需 1 次，找 11 需 2 次
5	空（无关键字）	-
6	6	找 6 需 1 次

• 老师强调：链地址法的查找次数 =“表头到目标关键字的节点数”，冲突仅影响链表内部，不影响其他地址，无淤积问题。

（3）建立公共溢出区

①定义

设置两个表：

• 基本表：存储 Hash 地址无冲突的关键字（地址范围 0~m-1）；
• 公共溢出区：存储所有与基本表关键字冲突的关键字（单独的向量）。
• 老师解释：“专门建一个‘备用区’，所有冲突的关键字都去备用区，基本表只存‘无争议’的关键字”。

②详细例子（对应表 7-XX 基本表与溢出表）

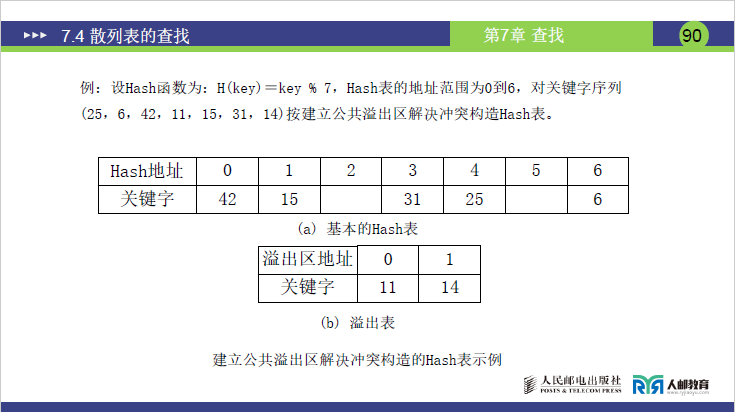
题目：同链地址法例子（H(key)=key%7，关键字序列(25,6,42,11,15,31,14)）。

步骤 1：构建基本表

存储无冲突的关键字，冲突的（14、11）放入溢出区：

Hash 地址	0	1	2	3	4	5	6
关键字	42	15	空	31	25	空	6

步骤 2：构建溢出区

存储冲突的关键字（14、11）：

溢出区地址	0	1
关键字	11	14

• 查找逻辑：先查基本表，若找不到且基本表对应地址有冲突记录，再查溢出区（顺序查找溢出区）。

（4）再 Hash 法

①定义

冲突发生时，换一个新的 Hash 函数重新计算关键字的地址，即、、、，直到找到空闲地址。

• 老师解释：“第一次算的地址被占，就换个公式再算，直到找到空地址”。

②特点

• 优点：无淤积现象；
• 缺点：增加 Hash 函数计算时间，多次计算可能影响效率，应用较少。

7.4.3 知识 3：散列查找性能分析（课件 92 页）

散列查找的理论时间复杂度是O(1)（直接通过 Hash 地址定位），但冲突会导致实际平均查找长度（ASL）大于 1。性能主要与装填因子*α*、Hash 函数、处理冲突方法有关。

（1）核心指标：装填因子α

α=mn（n为关键字个数，m为 Hash 表长度）：

• α越小：表中空闲单元多，冲突概率低，但空间浪费多；
• α越大：表中单元利用率高，但冲突概率高，ASL 增大；
• 老师建议：实际应用中α通常取 0.6~0.8，兼顾空间与效率。

（2）不同处理冲突方法的 ASL

①线性探查法

成功查找的平均查找长度：ASL=21(1+1−α1)

• 例：若α=0.7，则ASL≈21(1+0.31)≈2.17。

②链地址法

成功查找的平均查找长度：ASL=1+2α

• 例：若α=0.7，则ASL≈1+20.7=1.35，优于线性探查。
• 老师总结：链地址法的 ASL 普遍低于开放地址法，且无淤积，是更常用的冲突处理方式。

7.4.4 综合举例：多种查找方法对比

题目：给定关键字序列(11,78,10,1,3,2,4,21)，分别用顺序查找、二分查找、二叉排序树查找、平衡二叉树查找、散列查找（线性探查 + 链地址法） 实现查找，要求：

1. 画出对应存储结构（顺序表、判定树、二叉树、散列表）；
2. 计算成功查找的 ASL（假设每个关键字查找概率相等）；
3. 散列查找的 Hash 函数为H(key)=key%11（地址范围 0~10）。

（1）顺序查找

①存储结构：顺序表（一维数组）

数组下标	0	1	2	3	4	5	6	7
关键字	11	78	10	1	3	2	4	21

②ASL 计算

顺序查找的比较次数 = 关键字在数组中的 “下标 + 1”（第 1 个元素比 1 次，第 2 个比 2 次，…，第 8 个比 8 次）：ASL_Succ=81+2+3+4+5+6+7+8=836=4.5

• 老师提示：公式可简化为2n+1（n=8时，28+1=4.5），与计算结果一致。

（2）二分查找

①前提：关键字有序排列

先将序列排序为(1,2,3,4,10,11,21,78)（共 8 个元素，地址 0~7）。

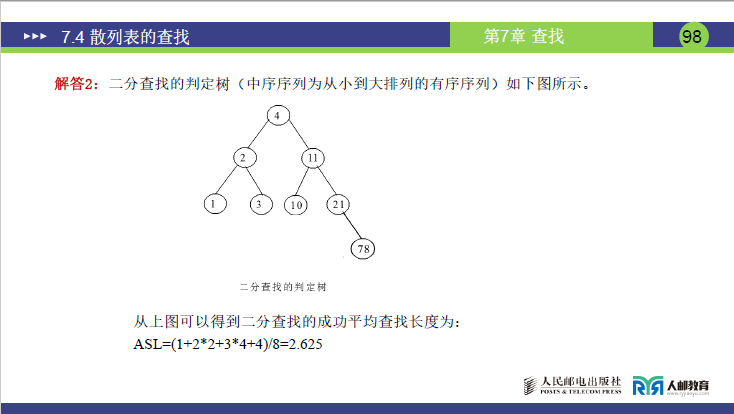
②存储结构：判定树

判定树的构建规则：每次取区间中点为根，左区间为左子树，右区间为右子树：

• 根节点（第 1 层）：4（下标 3），比较 1 次；
• 第 2 层：2（下标 1）、11（下标 5），各比较 2 次；
• 第 3 层：1（下标 0）、3（下标 2）、21（下标 6）、78（下标 7），各比较 3 次；
• 第 4 层：10（下标 4），比较 4 次。

③ASL 计算

ASL_Succ=81×1+2×2+3×4+4×1=81+4+12+4=821=2.625

• 对比：二分查找 ASL（2.625）远小于顺序查找（4.5），但仅适用于有序表，且需随机访问（数组存储）。

（3）二叉排序树查找（课件 99-104 页）

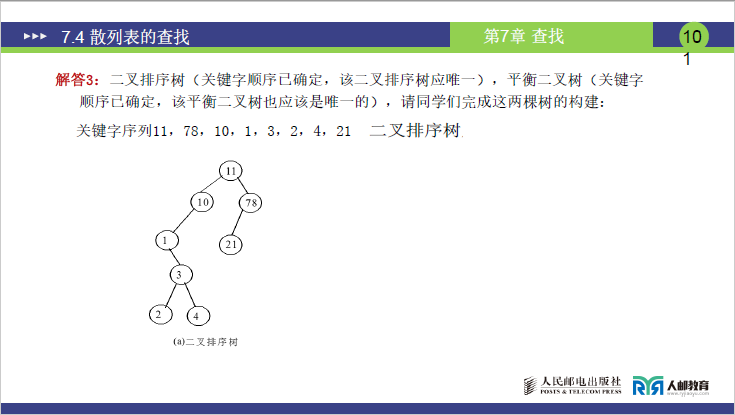
①存储结构：二叉排序树

构建规则：以第一个关键字为根，小于根的放左子树，大于根的放右子树：

• 根：11；
• 11 的右子树：78（78>11），78 的左子树：21（21<78）；
• 11 的左子树：10（10<11），10 的左子树：1（1<10），1 的右子树：3（3>1）；
• 3 的左子树：2（2<3），3 的右子树：4（4>3）。

②ASL 计算

各关键字的比较次数 = 所在层数：

• 11（1 次）、78（2 次）、10（2 次）、21（3 次）、1（3 次）、3（4 次）、2（5 次）、4（5 次）；ASL_Succ=81+2+2+3+3+4+5+5=825=3.125
• 老师提醒：二叉排序树可能退化（如关键字有序时退化为链表，ASL=O (n)），需平衡二叉树优化。

（4）平衡二叉树查找

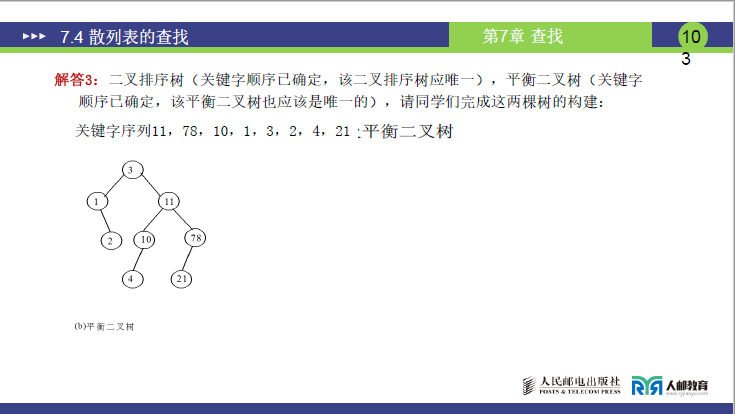
①存储结构：平衡二叉树

构建规则：保证每个节点的左右子树深度差≤1（平衡因子为 0、1、-1），需通过 LL、LR、RR、RL 旋转调整：

• 最终平衡树结构：根为 3，左子树 1（平衡因子 0），右子树 11（平衡因子 0）；
• 1 的左子树 2（平衡因子 0），1 的右子树 4（平衡因子 0）；
• 11 的左子树 10（平衡因子 0），11 的右子树 78（平衡因子 0），78 的左子树 21（平衡因子 0）。

②ASL 计算

各关键字的比较次数 = 所在层数（均为 3 次或 2 次）：ASLSucc≈82×2+6×3=84+18=2.75

• 总结：平衡二叉树避免退化，ASL 稳定为O(log₂n)，优于普通二叉排序树。

（5）散列查找（课件 105-108 页）

①线性探查法

• 步骤 1：计算 Hash 地址：

  11%11=0，78%11=1（78=11×7+1），10%11=10，1%11=1（冲突，探 2），3%11=3，2%11=2（冲突，探 4），4%11=4（冲突，探 5），21%11=10（冲突，探 9）；

• 步骤 2：构建散列表：

Hash 地址	0	1	2	3	4	5	6	7	8	9	10
关键字	11	78	1	3	2	4	空	空	空	21	10

• ASL 计算：

  11（1 次）、78（1 次）、1（2 次）、3（1 次）、2（3 次）、4（2 次）、21（8 次）、10（1 次）；

  ASL_Succ=81+1+2+1+3+2+1+8=819=2.375

②链地址法

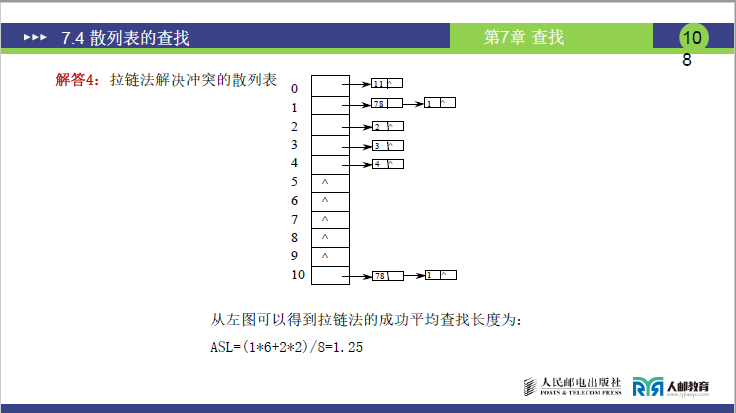
• 步骤 1：计算 Hash 地址：

  11%11=0，78%11=1，10%11=10，1%11=1，3%11=3，2%11=2，4%11=4，21%11=10；

• 步骤 2：构建散列表：

Hash 地址	链表结构	比较次数
0	11	1
1	78 → 1	1（78）、2（1）
2	2	1
3	3	1
4	4	1
5-9	空	-
10	10 → 21	1（10）、2（21）

• ASL 计算：ASL_Succ=81×6+2×2=86+4=1.25
• 老师强调：链地址法的 ASL（1.25）是所有方法中最低的，体现了散列查找的高效性。

7.4.5 方法对比总结

查找方法	时间复杂度	ASL（本题 n=8）	适用场景
顺序查找	O(n)	4.5	无序表、链表存储
二分查找	O(log₂n)	2.625	有序数组，静态查找
二叉排序树	O(log₂n)~O(n)	3.125	动态查找（需插入 / 删除）
平衡二叉树	O(log₂n)	≈2.75	动态查找，需稳定高效
散列（线性探查）	O(1)	2.375	中等冲突，空间有限
散列（链地址）	O(1)	1.25	高冲突，需高效低淤积

• 核心结论：散列查找（尤其是链地址法）在平均性能上最优，是动态查找的首选；平衡二叉树适用于需有序遍历的场景；二分查找适用于静态有序表。

参考资料：教材《数据结构 C 语言 第 3 版》 数据结构考研指导（基础篇） 、数据结构考研指导（基础篇） 视频课程｜赵海英