第6章图

6.1 图的定义和基本数据

6.1.1 图的定义

（1）图的核心定义

图是一种由 “顶点” 和 “顶点间关系（边 / 弧）” 构成的数据结构，用二元组定义为 G=(V,E)，其中：

V：顶点集（Vertex Set），由图中所有不重复的顶点组成；
E：边集（Edge Set），由顶点间的关联关系（边或弧）组成。

（2）无向图与有向图的定义及二元组表示

类型	核心特征	二元组表示示例	符号区别
无向图	边无方向性，无箭头标识	无向图G1=(V1,E1)，其中V1={a,b,c,d}，E1={(a,b),(a,c),(a,d),(b,d),(c,d)}	边集元素用小括号 ()表示，代表两点间无向边
有向图	边有方向性，用箭头标识（边称为 “弧”）	有向图G2=(V2,E2)，其中V2={1,2,3}，E2=	弧集元素用尖括号 <> 表示，尖括号内前者为弧尾（箭头起点）、后者为弧头（箭头终点）

6.1.2 图的基本术语

（1）有向图与无向图（基础分类）

有向图：边有方向性，边称为弧，有明确的弧尾（起点）和弧头（终点），用箭头标识。
无向图：边无方向性，仅表示两点间存在连接，无箭头标识。

（2）完全图、稠密图、稀疏图

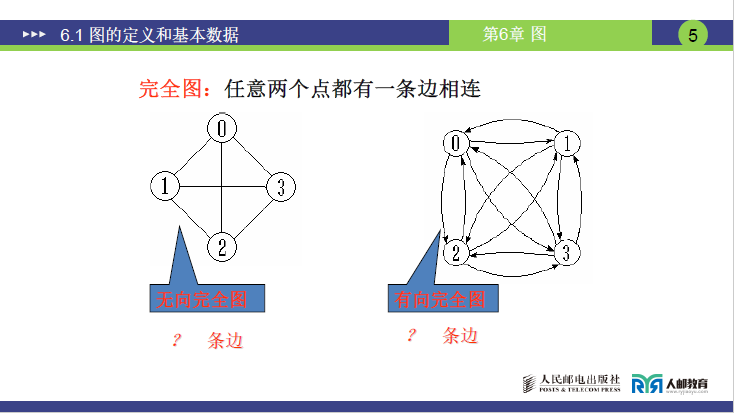
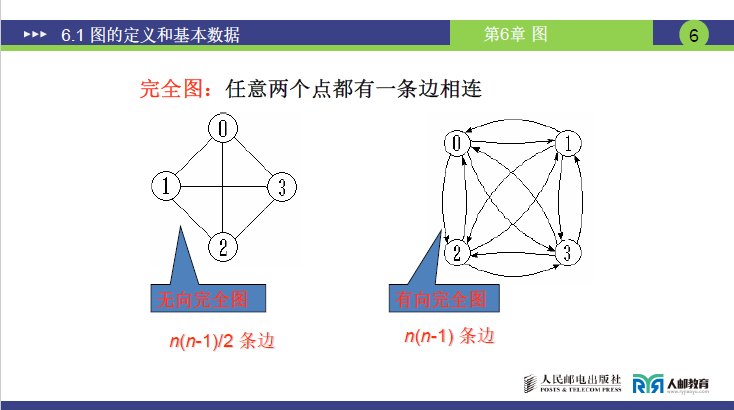
①完全图

定义：任意两个顶点之间都存在边（无向图）或弧（有向图）的图，分为无向完全图和有向完全图。

无向完全图：n个顶点的无向完全图，边数为组合数C_n²=n(n−1)/2（推导：任意两点仅需 1 条无向边连接，共需从n个顶点选 2 个的组合数）。例如 4 个顶点的无向完全图，边数为4×3/2=6。
有向完全图：n个顶点的有向完全图，弧数为排列数A_n²=n(n−1)（推导：两点间需 2 条方向相反的弧，弧数为无向完全图边数的 2 倍）。例如 4 个顶点的有向完全图，弧数为4×3=12。
共同特征：完全图的边 / 弧数达到对应图类型的 “最大值”，课件中完全图示例的邻接矩阵（后续内容）对角元素为 0（顶点自身无关联），其余元素为 1。

②一般图的边 / 弧数范围

无向图：顶点数为n，边数e满足0≤e≤n(n−1)/2（最少 0 条边，最多无向完全图的边数）；
有向图：顶点数为n，弧数e满足0≤e≤n(n−1)（最少 0 条弧，最多有向完全图的弧数）。

③稠密图与稀疏图

稠密图：边 / 弧数接近对应完全图边 / 弧数的图。
稀疏图：边 / 弧数远少于对应完全图边 / 弧数的图（讲课表述中 “析出符” 为口误，实际为稀疏图）。

（3）度、入度、出度

①度的通用定义

图中一个顶点依附的边或弧的数目，称为该顶点的度。

②有向图的入度与出度

有向图中顶点的度为入度与出度之和，具体定义如下：

入度：顶点依附的弧头（箭头指向该顶点）的数目，代表进入该顶点的弧的数量。
出度：顶点依附的弧尾（箭头从该顶点出发）的数目，代表从该顶点发出的弧的数量。

③无向图的度

无向图中无入度、出度之分，顶点的度即为其相连的边的数目。

④典型问题：特殊有向图的形状

若有向图中仅 1 个顶点入度为 0，其余顶点入度均为 1，则该图为有向树（入度为 0 的顶点为树根，其余顶点对应树的子节点，有唯一的双亲节点）。

（4）连通图与强连通图

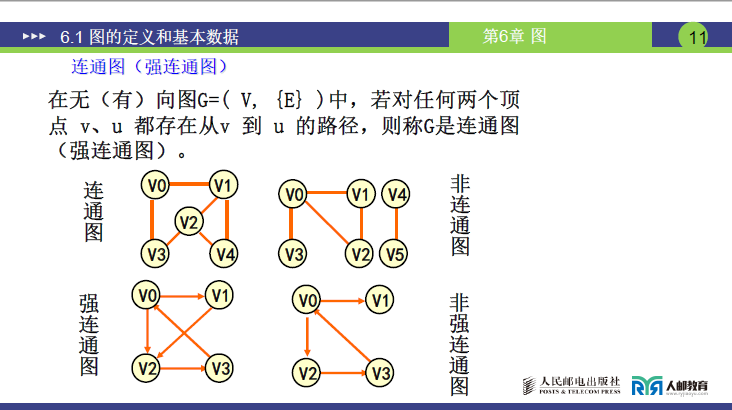
类型	适用图	核心定义
连通图	无向图	图中任意两个顶点v和u 都存在从v到u的路径
强连通图	有向图	图中任意两个顶点v和u 都存在双向路径（既存在v到u的路径，也存在u到v的路径）

反例：若无向图中存在两个顶点组（如V₀−V₁−V₂−V₃和V₄−V₅），两组内顶点互通但组间无路径，则为非连通图；有向图中若存在顶点对无双向路径（如V₁无法到V₂），则为非强连通图。

（5）网

图的边 / 弧上附带的相关数值称为权（可表示距离、耗费等），带权的图称为网，也叫有权图。

（6）子图

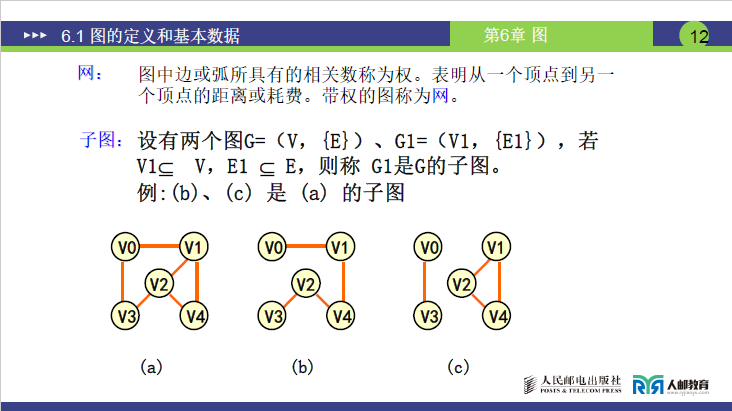
设两个图G=(V,{E})和G1=(V₁,{E₁})，若满足V₁⊆V且E₁⊆E，则称G₁是G的子图。例如课件中图 (a) 的顶点和边的部分子集构成的图 (b)、图 (c)，均为图 (a) 的子图。

6.2 图的存储结构

6.2.1 邻接矩阵（顺序存储，底层为二维数组）

（1）邻接矩阵的定义

邻接矩阵是基于二维数组的顺序存储结构，用于存储图的顶点信息和顶点间的关系：

顶点信息：用一个一维数组（顶点表）存储所有顶点；
顶点关系：用一个n×n的二维数组（邻接矩阵）存储，其中n为顶点数。

邻接矩阵的元素定义为：

\[A[i][j] = \begin{cases} 1 & \text{若}(i,j) \in E(G) \text{或} <i,j> \in E(G) \\ 0 & \text{其它情形} \end{cases} \]

邻接矩阵通过顶点表存储顶点本身信息，通过二维矩阵存储顶点间的邻接关系：

若两顶点间存在边 / 弧，矩阵对应位置值为1（普通图）或边 / 弧的权值（网）；
若不存在边 / 弧，普通图对应位置为0，网对应位置为 ∞；
顶点自身到自身（主对角线）：考试建议记为0，教材通常记为 ∞，需注意题目约定。

（2）不同类型图的邻接矩阵表示

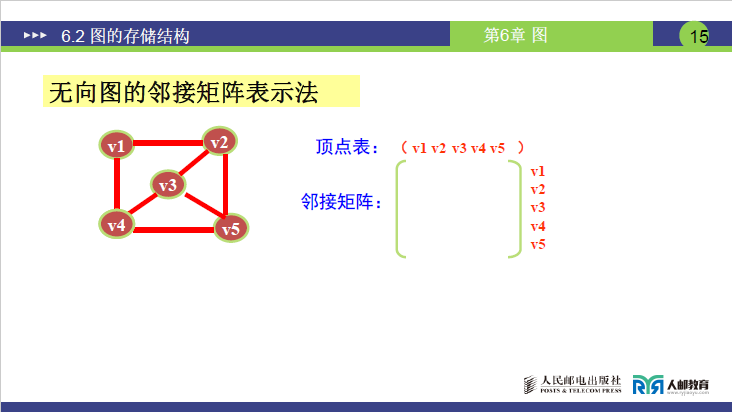
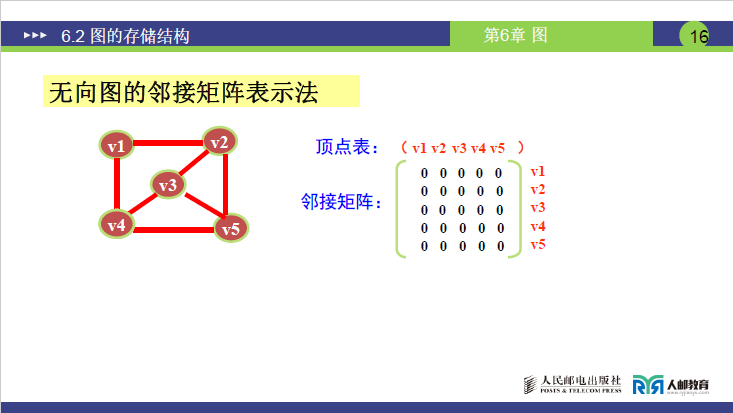
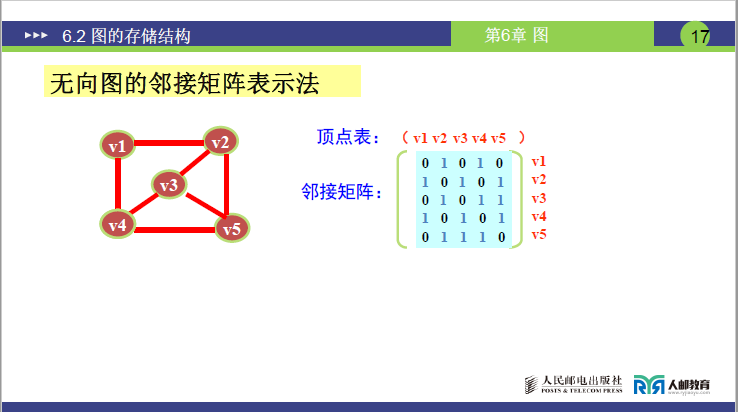
①无向图的邻接矩阵

构建步骤：

① 按顶点数构建n×n矩阵（5 顶点为5×5），初始化全为 0；

② 若顶点V_i与V_j有边，将矩阵[i][j]和[j][i]置为 1（无向边双向对称）。
讲课易错点：无向图 7 条边对应矩阵 14 个 1（每条边被双向记录，边数 = 矩阵中 1 的个数 / 2）。
核心特点：
1. 矩阵对称；
2. 第i行或第i 列1的个数为顶点i 的度；
3. 完全无向图的邻接矩阵主对角线为 0，其余位置全为 1；
4. 矩阵中1的个数的一半为图中边的数目
5. 可通过[i][j]是否为 1，快速判断Vi与Vj是否有边;
6. 占用的存储单元数目为n+2e。

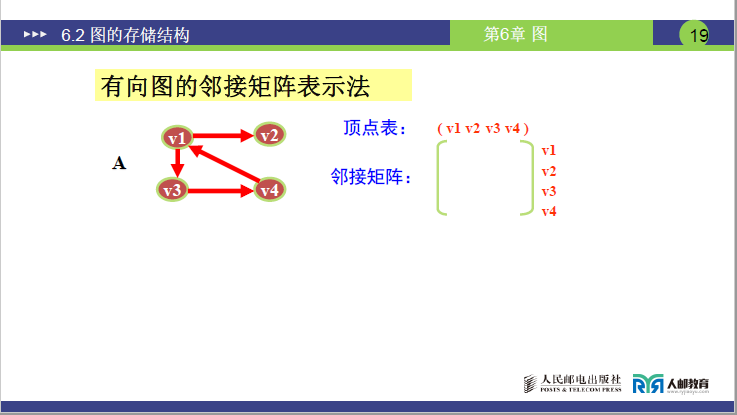
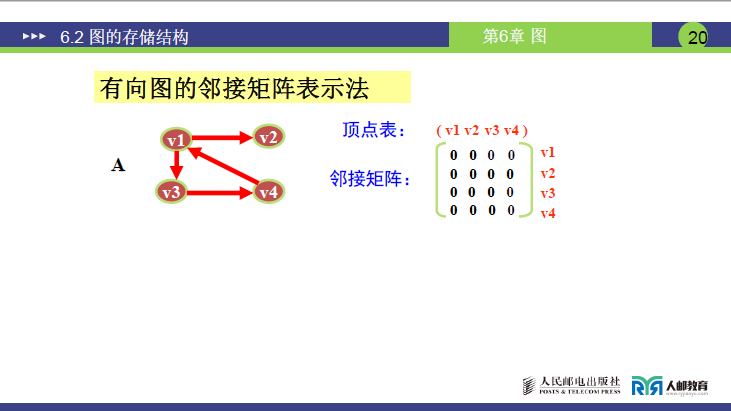
②有向图的邻接矩阵

构建约定：矩阵记录顶点发出去的弧（出度边），即[i][j]=1表示存在<Vi,Vj>的弧。
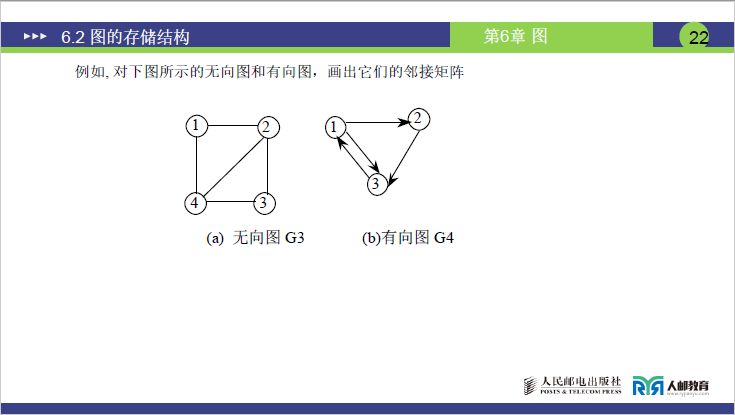
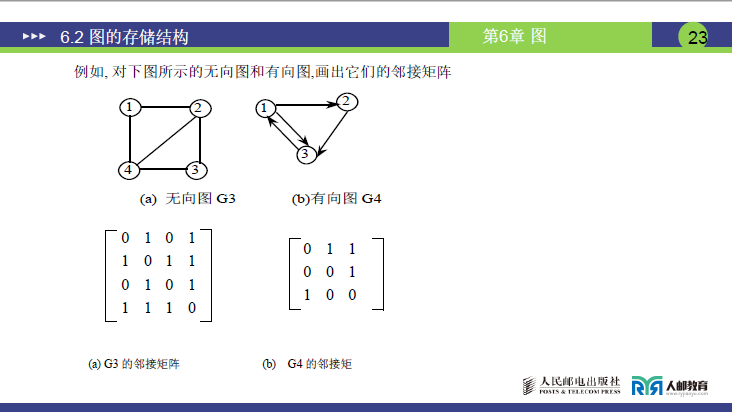
构建步骤（以4 顶点有向图为例）：

① 构建4×4矩阵并初始化全为 0；

② 若Vi发出弧至Vj，仅将[i][j]置为 1（入度边不记录在该行）。
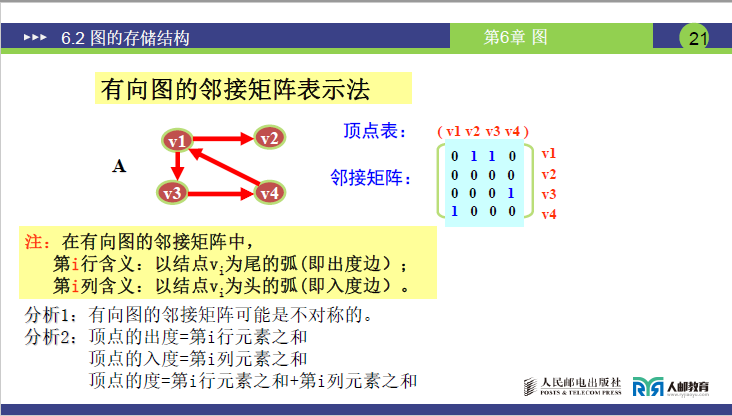
核心特点：
1. 矩阵不一定对称（有向弧单向性）；
2. 顶点i的出度= 第i行 1 的个数，入度= 第i列 1 的个数，总度数 = 出度 + 入度；
3. 矩阵中 1 的个数 = 图中弧的总数（无重复记录）；
4. 完全有向图的邻接矩阵主对角线为 0，其余位置全为 1；
5. 很容易判断顶点i 和顶点j 是否有弧相连。

结论

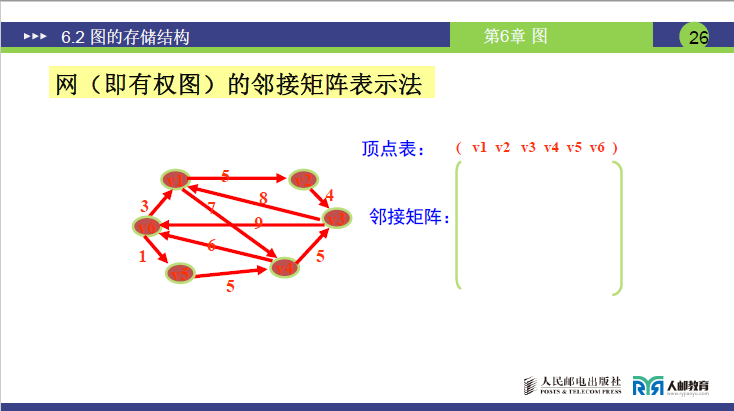
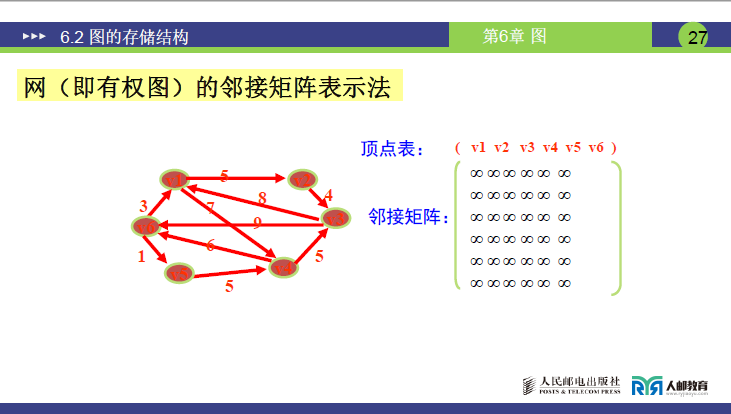
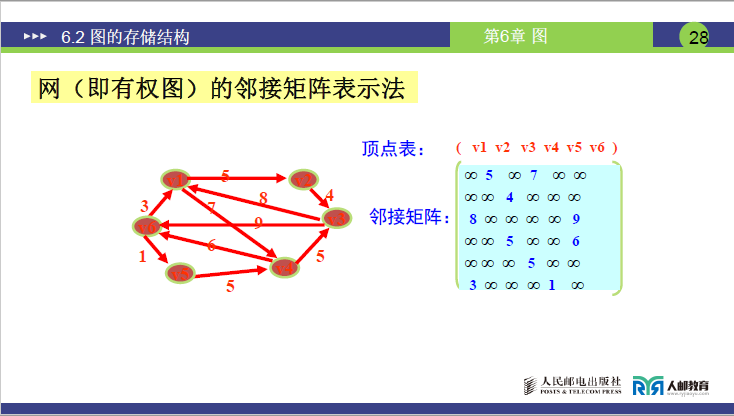
③网的邻接矩阵（带权图）

定义公式：

\[A[i][j] = \begin{cases} w_{ij} & \text{若}(i,j) \in E(G) \text{或} <i,j> \in E(G) \\ 0 & \text{若} i = j \\ \infty & \text{其它情形} \end{cases} \]
构建注意事项（讲课重点强调）：

① 权值w_ij替换普通图的 “1”，表示两顶点间边的权重；

② 主对角线的 0/∞需按题目要求选择（考试优先用 0）；

③ 无向网矩阵对称，有向网矩阵不对称。

（3）邻接矩阵的优缺点（扩展补充）

优点：判断两顶点是否邻接效率高（O (1)）；计算顶点度（无向图）、出 / 入度（有向图）方便；
缺点：空间复杂度高（O (n²)），适合存储稠密图；稀疏图会造成大量空间浪费。

6.2.2 邻接表（链式存储，头节点 + 表节点）

（1）邻接表的存储结构（课件定义）

把同一个顶点发出的边链接在同一个边链表中，链表的每一个结点代表一条边，叫做表结点（边结点），邻接点域adjvex保存与该边相关联的另一顶点的顶点下标，链域next存放指向同一链表中下一个表结点的指针，数据域weight存放边的权。边链表的表头指针存放在头结点中。头结点以顺序结构存储，其数据域info存放顶点信息，链域first指向链表中第一个顶点

邻接表由头节点数组和表节点链表组成，网的表节点需额外增加权值域：

节点类型	结构组成	说明
头节点	`data`（顶点信息）+`firstarc`（指向首个表节点的指针）	按顶点顺序存储，形成头节点数组
普通图表节点	`adjvex`（邻接点的顶点下标）+`nextarc`（指向下一表节点的指针）	存储顶点的出度边 / 邻接边
网的表节点	`adjvex`+`weight`（边的权值）+`nextarc`	比普通图表节点多权值域，记录边的权重

（2）不同类型图的邻接表表示

①无向图的邻接表

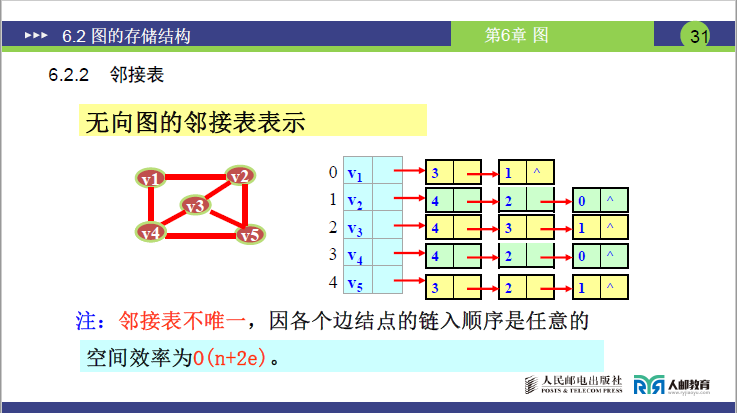
构建逻辑：每个顶点的头节点链表，存储所有与该顶点邻接的顶点下标（无向边双向存储，如V_i邻接V_j，则V_i链表有j，V_j链表有i）。
讲课示例：5 顶点无向图中，V₁的表节点为 V₂（下标 3）、V₄（下标 1），顺序可任意。
核心特点：
1. 邻接表表示不唯一（表节点链入顺序可自由调整）；
2. 第i个头节点的链表节点数 = 顶点i的度；
3. 所有表节点总数 = 2× 边数（无向边双向记录）；
4. 空间复杂度为O(n+2e)（n 为顶点数，e 为边数）。

②有向图的邻接表与逆邻接表

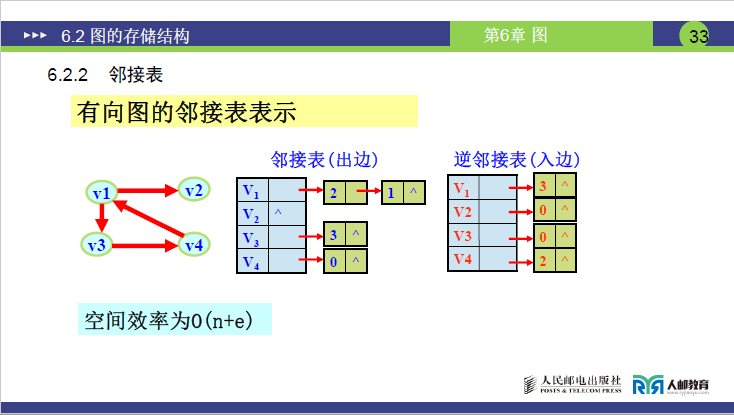
邻接表（出边表）：

① 存储逻辑：仅记录顶点的出度边，即表节点为顶点发出弧的终点下标；

② 特点：第i个头节点的链表节点数 = 顶点i的出度；空间复杂度为O(n+e)（每条弧仅记录一次）；无法直接求入度。
逆邻接表（入边表）：

① 存储逻辑：记录顶点的入度边，即表节点为指向该顶点的弧的起点下标；

② 作用：解决有向图邻接表无法直接求入度的问题，第i个头节点的链表节点数 = 顶点i的入度。
讲课易错点：无特殊说明时，有向图邻接表默认指出边表。

③网的邻接表

构建逻辑：表节点增加weight域存储边的权值，其余结构与普通有向 / 无向图邻接表一致；
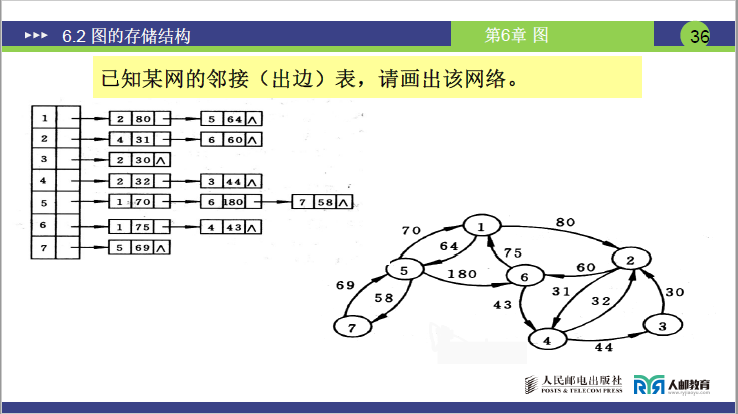
讲课典型例题：已知网的邻接表重构网

① 核心方法：根据头节点的顶点信息，遍历每个头节点的表节点，按adjvex（邻接点下标）和weight（权值）绘制带权边；

② 意义：验证了存储结构可反向恢复逻辑结构，体现数据结构 “存储 - 还原” 的核心价值。

（3）邻接表的优缺点

优点：空间利用率高（O (n+e)），适合存储稀疏图；便于遍历顶点的邻接边；
缺点：判断两顶点是否邻接效率低（需遍历对应头节点的链表）；无向图存在边的重复存储。

6.2.3邻接矩阵与邻接表的核心对比

对比维度	邻接矩阵	邻接表
存储结构	二维数组（顺序存储）	头节点数组 + 链表（链式存储）
空间复杂度	O (n²)（与边数无关）	无向图 O (n+2e)、有向图 O (n+e)
邻接判断效率	O (1)（直接查矩阵下标）	O (d)（d 为对应顶点的度，需遍历链表）
顶点度计算	无向图：行 / 列 1 的个数；有向图：行 = 出度、列 = 入度	无向图：链表节点数；有向图：邻接表 = 出度、逆邻接表 = 入度
适用场景	稠密图、需快速判断邻接的场景	稀疏图、需频繁遍历邻接边的场景

6.2.4讲课中的考试与学习注意事项

邻接矩阵主对角线约定：考试建议主对角线记为 0，教材常用∞，需严格遵循题目要求；
有向图邻接矩阵的边数：矩阵中 1 的个数 = 弧的总数（无向图为 1 的个数 / 2）；
邻接表的唯一性：表节点顺序不影响存储有效性，因此同一图的邻接表表示不唯一；
知识衔接：掌握图的存储结构后，后续将学习图的核心操作 ——图的遍历（深度优先 / 广度优先），为后续最小生成树、最短路径等应用打基础。

6.3 图的遍历

6.3.1图的遍历概述

（1）定义

从图中某一顶点出发，访遍图中其余所有顶点且每个顶点仅被访问一次的操作，称为图的遍历。

（2）核心意义

图的遍历算法是求解图的连通性问题、拓扑排序、关键路径等后续图应用算法的基础，是图论算法体系的核心前置知识点。

（3）两种经典遍历方法

深度优先搜索（DFS）遍历、广度优先搜索（BFS）遍历，两种方法均可实现对图中所有顶点的不重复访问，且遍历序列不唯一。

6.3.2 深度优先搜索（DFS）遍历

（1）算法核心思想

深度优先搜索的本质是 “递归 + 回退”，通过 “优先访问当前顶点的未访问邻居，直到无邻居可访问时回退到上一顶点”

（2）算法执行步骤（标准流程）

首先访问起始顶点i，将其访问标记置为已访问，即visited[i] = 1（初始化时所有visited[]均为 0）；
搜索与顶点i有边相连的下一个顶点j：
- 若j未被访问（visited[j] = 0），则访问j并置visited[j] = 1，然后从j开始重复步骤 2（递归深入）；
- 若j已被访问（visited[j] = 1），则继续检查与i有边相连的其他顶点；
若与i有边相连的所有顶点均已访问，则回退到上一个访问过的顶点，重复步骤 2，直到图中所有顶点都被访问完毕。

（3）辅助存储结构

遍历过程需借助栈实现回溯，栈遵循 “后进先出” 原则，用于记录访问路径，当当前顶点分支探索完毕时，从栈中弹出顶点实现回溯。

（4）典型示例（无向图 G7，从顶点 0 出发）

①图的背景

无向图 G7 包含顶点 0、1、2、3、4、5、6（课件页码 3-4 的图 6-13 中，顶点连接关系：0 连 1、2、3；1 连 0、4、5、6；4 连 1、5；5 连 1、4；6 连 1、2；2 连 0、6；3 连 0）。

②以顶点 0 为起始点的遍历过程（讲课内容补充）

按 “0→1→4→5→回退→1→6→2→回退→0→3” 的顺序展开，每一步跟踪visited数组和回退逻辑：

初始状态：visited = [0,0,0,0,0,0,0]，起始顶点选 0；
- 访问 0，visited[0] = 1，0 的邻居为 1、2、3（任选 1，讲课中选 1）；
访问 1，visited[1] = 1，1 的邻居为 0（已访问）、4、5、6（任选 4）；
访问 4，visited[4] = 1，4 的邻居为 1（已访问）、5（未访问，选 5）；
访问 5，visited[5] = 1，5 的邻居为 1（已访问）、4（已访问）→ 无未访问邻居，回退到 4；
回退到 4 后，4 的邻居均已访问→ 继续回退到 1；
1 的邻居中，0、4、5 已访问，剩余 6（未访问）→ 访问 6，visited[6] = 1；
6 的邻居为 1（已访问）、2（未访问）→ 访问 2，visited[2] = 1；
2 的邻居为 0（已访问）、6（已访问）→ 无未访问邻居，回退到 6；
6 的邻居均已访问→ 回退到 1，1 的邻居均已访问→ 回退到 0；
0 的邻居中，1、2 已访问，剩余 3（未访问）→ 访问 3，visited[3] = 1；
3 的邻居为 0（已访问）→ 无未访问邻居，遍历结束。

③遍历序列与唯一性分析

上述过程的遍历序列：0→1→4→5→6→2→3；
序列不唯一的原因：
1. 起始顶点可选（如选 1、2、3 为起始点，序列完全不同）；
2. 邻居顶点选择顺序可换（如 0 的邻居先选 2 而非 1，序列会变为0→2→6→1→4→5→3；1 的邻居先选 5 而非 4，序列会变为0→1→5→4→6→2→3）；
考试判断序列正确性的方法：检查序列是否符合 “访问当前顶点→递归访问未访问邻居→回退” 的逻辑，只要每一步都能通过 “当前顶点的未访问邻居” 推导到下一个顶点，即为正确序列（如讲课中提到的0→3→2→6→1→5→4也是正确序列）。

（5）关键结论与考点

遍历起点可任意选择，考试中常指定起点；
同一顶点的多个未访问邻接顶点可任选访问顺序，因此DFS 遍历序列不唯一；
考试常考 “判断给定序列是否为合法 DFS 遍历序列”，需验证序列是否符合 “先深后广、回溯探索” 的逻辑。

6.3.3 广度优先搜索（BFS）遍历

（1）算法核心思想

遵循 “先广后深、分层访问” 的原则，先访问起始顶点的所有邻接顶点（同层顶点），再依次访问各邻接顶点的邻接顶点（下一层顶点）。

（2）算法执行步骤（课件标准流程）

初始化队列，将其置空；
选择起始顶点，访问该顶点并置visited[起始顶点] = 1，将其入队；
若队列非空：
- 将队首顶点出队，遍历其所有有边相连的顶点j；
- 若j未被访问，则访问j并置visited[j] = 1，将j入队；
重复步骤 3，直到队列为空：
- 若此时所有顶点均已访问，遍历结束；
- 若仍有未访问顶点，需另选新的起始顶点（针对非连通图），重复步骤 2-3。

关键区别：与深度优先搜索的辅助结构对比

遍历方式	辅助结构	结构特性	遍历逻辑
深度优先搜索	栈（或递归栈）	后进先出（LIFO）	一条路走到底，走不通回退
广度优先搜索	队列	先进先出（FIFO）	一层一层扩散，先扫邻居

（3）辅助存储结构

遍历过程需借助队列实现分层访问，队列遵循 “先进先出” 原则，保证同层顶点按入队顺序依次处理。

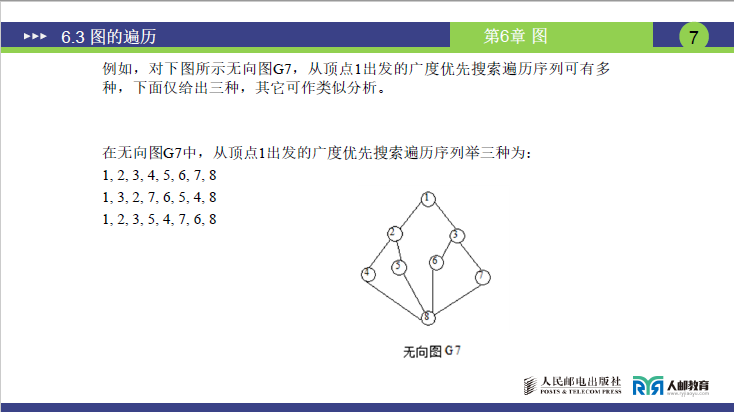
（4）典型示例（无向图 G7，从顶点 1 出发）

①图的背景

同深度优先遍历的无向图 G7（顶点 0-6，连接关系不变；讲课中补充顶点 8，推测为课件图中遗漏标注，实际连接：4 连 8、5 连 8、6 连 8、7 连 8，7 连 3）。

②以顶点 1 为起始点的遍历过程（讲课内容补充）

按 “队列进出 + 层次访问” 展开，每一步跟踪队列状态和visited数组：

初始状态：visited = [0,0,0,0,0,0,0,0,0]，队列空，起始顶点选 1；
- 访问 1，visited[1] = 1，1 入队→ 队列：[1]；
队首 1 出队，遍历 1 的邻居：0（未访问）、2（未访问）、3（未访问）、4（未访问）、5（未访问）、6（未访问）（讲课中选 2、3 优先）；
- 访问 2，visited[2] = 1，2 入队；访问 3，visited[3] = 1，3 入队→ 队列：[2,3]；
队首 2 出队，遍历 2 的邻居：0（未访问）、6（未访问）（1 已访问）；
- 访问 6，visited[6] = 1，6 入队；访问 0，visited[0] = 1，0 入队→ 队列：[3,6,0]；
队首 3 出队，遍历 3 的邻居：0（已访问）、7（未访问）；
- 访问 7，visited[7] = 1，7 入队→ 队列：[6,0,7]；
队首 6 出队，遍历 6 的邻居：1（已访问）、2（已访问）、8（未访问）；
- 访问 8，visited[8] = 1，8 入队→ 队列：[0,7,8]；
队首 0 出队，遍历 0 的邻居：1（已访问）、2（已访问）、3（已访问）→ 无未访问邻居→ 队列：[7,8]；
队首 7 出队，遍历 7 的邻居：3（已访问）、8（未访问？8 未访问则访问 8，已访问则跳过）→ 8 已访问→ 队列：[8]；
队首 8 出队，遍历 8 的邻居：4（未访问）、5（未访问）、6（已访问）、7（已访问）；
- 访问 4，visited[4] = 1，4 入队；访问 5，visited[5] = 1，5 入队→ 队列：[4,5]；
队首 4 出队，遍历 4 的邻居：1（已访问）、5（未访问？5 未访问则访问，已访问则跳过）、8（已访问）→ 5 已访问→ 队列：[5]；
队首 5 出队，遍历 5 的邻居：1（已访问）、4（已访问）、8（已访问）→ 无未访问邻居→ 队列空，遍历结束。

③遍历序列与唯一性分析（课件页码 7）

课件给出 3 种正确序列：
1. 1,2,3,4,5,6,7,8；
2. 1,3,2,7,6,5,4,8；
3. 1,2,3,5,4,7,6,8；
序列不唯一的核心原因：同一层顶点的访问顺序可换（如步骤 2 中 1 的邻居先选 3 再选 2，序列变为1,3,2,...；步骤 8 中 8 的邻居先选 5 再选 4，序列变为...,5,4,...）；
序列正确性判断：检查是否符合 “层次遍历” 逻辑 ------当前顶点的所有邻居（同一层）必须在邻居的邻居（下一层）之前访问（如1的邻居 2、3 必须在 2 的邻居 6、0 之前访问，3 的邻居 7 必须在 6 的邻居 8 之前访问）。

（5）快速判断合法 BFS 序列的技巧

可将遍历序列按 “层” 划分：起始顶点为第 0 层，其邻接顶点为第 1 层，第 1 层顶点的邻接顶点为第 2 层，以此类推。同层顶点的顺序可任意互换，只要满足 “先访问上层顶点，再访问下层顶点” 即可判定为合法序列。

（6）两种遍历方法核心总结

对比维度	深度优先搜索（DFS）	广度优先搜索（BFS）
辅助结构	栈（或递归栈）	队列
遍历顺序	深度优先（一条路走到底）	广度优先（一层一层扩散）
序列唯一性	不唯一（起始点 + 邻居选择）	不唯一（起始点 + 同层顺序）
适用场景	连通性判断、迷宫求解	最短路径（无权图）、层次分析
核心逻辑	递归 + 回退	队列进出 + 层次访问

6.4 图的应用

6.4.1. 生成树和最小生成树

（1）课程引入：图的核心应用方向

上一节学习了图的两种遍历算法（深度优先搜索 DFS、广度优先搜索 BFS），是图应用的基础。本节课进入图的核心应用模块，考试中涉及的图算法共 7 个，重点掌握 4 个核心方向：

最小生成树（本节课重点）
最短路径（后续课程）
拓扑排序（后续课程）
关键路径（后续课程）

图的应用核心思想：将复杂的 “图” 简化为已掌握的结构（如树、线性表）解决，例如树可简化为二叉树，图可简化为树（生成树），再进一步解决 “最小”“最短” 等优化问题。

（2）生成树和最小生成树

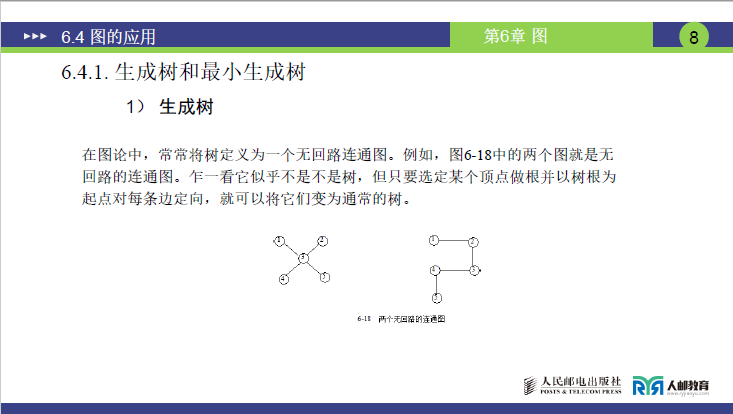
①生成树的定义与本质

1. 课件核心定义

树的图论定义：无回路的连通图（无环且所有顶点连通）。
生成树的概念：从任意连通图中提取的子图，满足两个条件：

（1）包含原图所有顶点；

（2）保持连通且无回路（符合树的定义）；

（3）顶点数为n时，边数必为n-1（树的顶点 - 边关系）。

2. 图与树的区别

特征	树（生成树的基础）	图（生成树的来源）
顶点关系	一对多（有根，唯一父节点）	多对多（无固定根，可双向连接）
回路（环）	无	可能有
核心特点	“甩顶点无珠子掉落”（连通无环，拎任意顶点，所有顶点都被边牵连）	可能 “有珠子掉落”（不连通）或 “形成圈”（有环）

3. 生成树的构造方法（衔接图的遍历）

课件隐含逻辑：通过图的遍历算法（DFS/BFS）可将连通图转化为生成树，对应两种生成树：

深度优先生成树（DFS 生成树）：基于深度优先遍历路径构建，优先 “深入” 未访问顶点。
广度优先生成树（BFS 生成树）：基于广度优先遍历路径构建，优先 “横向” 访问邻接顶点。

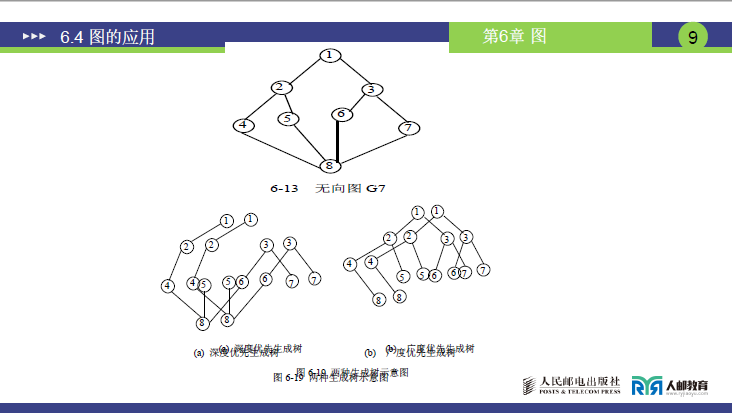
示例：无向图 G7 的生成树

图 6-19（a）深度优先生成树：顶点 1 为起点，遍历路径 1→2→4→8→5→3→6→7，边数 7（顶点 8 个，8-1=7），无环且连通；
图 6-19（b）广度优先生成树：顶点 1 为起点，遍历路径 1→2→3→4→7→5→6→8，边数 7，层级分明（如 1 的邻接顶点 2、3 先访问，再访问 2 的邻接 4 等）。

（3）最小生成树：带权图的 “最优” 生成树

①核心概念：从 “图” 到 “网”

网（带权图）：边附带权值的图（权值可表示距离、费用、时间等）；
最小生成树（Minimum Spanning Tree, MST）：在网的所有生成树中，所有边的权值之和最小的生成树。

②应用场景

实际问题：全国城市间铺设光缆，使所有城市连通且光缆总长度最短（费用最低）；
核心需求：保持连通性（无孤立顶点）、无回路（避免浪费）、权和最小（优化目标）。

③两种经典算法

课件明确提到两种求最小生成树的算法，本节课先详解普里姆算法，后续课程讲克鲁斯卡尔算法：

普里姆（Prim）算法：按 “顶点扩展” 思路，适合稠密图（边多顶点少）；
克鲁斯卡尔（Kruskal）算法：按 “边排序选优” 思路，适合稀疏图（边少顶点多）。

6.4.2 普里姆（Prim）算法：顶点扩展法求 MST

（1）算法核心思想

①三大集合定义

V：图中所有顶点的全集（固定不变）；
U：已加入最小生成树的顶点集合（初始任选一个顶点，逐步扩大）；
W：未加入最小生成树的顶点集合（W = V - U，逐步缩小至空）。

②核心步骤（循环执行至`W`为空）

初始化：任选顶点k（如课件选顶点 1），令U={k}，W=V-U；用虚线连接U中顶点与W中顶点，标注边权（无直接边则标∞，表示 “不可达”）；
选最短边：在U与W之间的所有虚线边中，选择权值最小的边，将其改为实线（加入生成树）；
扩展U：将步骤 2 中最短边的W端顶点（未选顶点）加入U，同时从W中删除该顶点；
修正边权：重新检查U与W之间的虚线边 —— 若新加入U的顶点能让U到W的某顶点的边权更小，则更新该边权（“留小去大”）；
终止条件：当W为空时，U=V，生成树构建完成（边数n-1）。

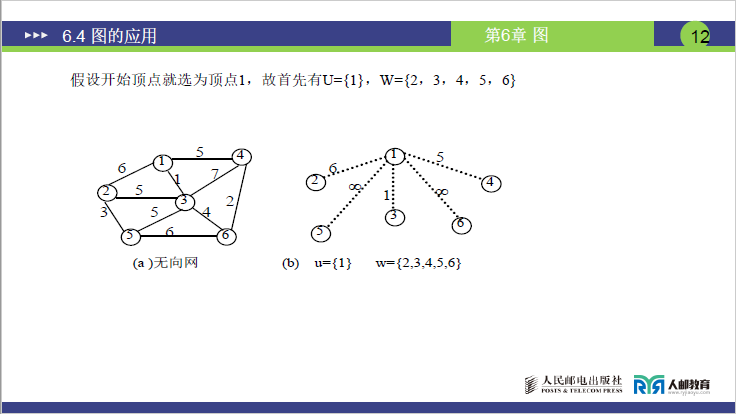
（2）实操示例：无向网（顶点 1-6）的 MST 构建（课件第 12-14 页图 6-20）

已知条件

无向网顶点：1、2、3、4、5、6；边权如下（课件图 6-20（a））：

1-2（6）、1-3（1）、1-4（5）；
3-2（5）、3-5（5）、3-6（4）；
6-4（2）、2-5（3）；
其余无直接边（如 1-5、1-6、4-2、4-5）标∞。

步骤 1：初始化（课件图 6-20（b），页码 12）

U={1}，W={2,3,4,5,6}；
虚线边及权值：1-2（6）、1-3（1）、1-4（5）、1-5（∞）、1-6（∞）；
核心：仅基于U中顶点 1 连接W，无其他顶点辅助。

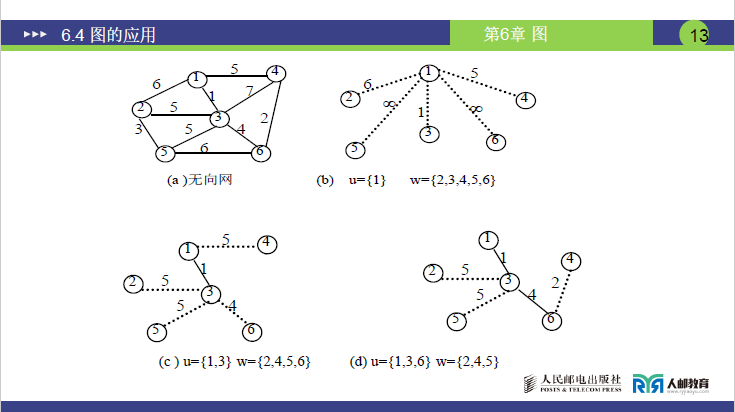
步骤 2：第一次选边与扩展（课件图 6-20（c））

选最短边：U-W间最小权边是 1-3（权 1），改实线；
扩展U：将 3（W中顶点）加入U，此时U={1,3}，W={2,4,5,6}；
修正边权：基于新加入的 3，更新U-W边权：
- 3-2（5）＜1-2（6）→ 删 1-2（6），改虚线 3-2（5）；
- 3-5（5）＜1-5（∞）→ 删 1-5（∞），改虚线 3-5（5）；
- 3-6（4）＜1-6（∞）→ 删 1-6（∞），改虚线 3-6（4）；
- 3-4（7）＞1-4（5）→ 保留虚线 1-4（5）；

结果：U有 2 个顶点，生成树有 1 条边（1-3）。

步骤 3：第二次选边与扩展（课件图 6-20（d））

选最短边：U-W间最小权边是 3-6（权 4），改实线；
扩展U：将 6 加入U，U={1,3,6}，W={2,4,5}；
修正边权：基于新加入的 6，更新U-W边权：
- 6-4（2）＜1-4（5）→ 删 1-4（5），改虚线 6-4（2）；
- 6-2（∞）＞3-2（5）→ 保留 3-2（5）；
- 6-5（6）＞3-5（5）→ 保留 3-5（5）；

结果：生成树新增边 3-6，共 2 条边。

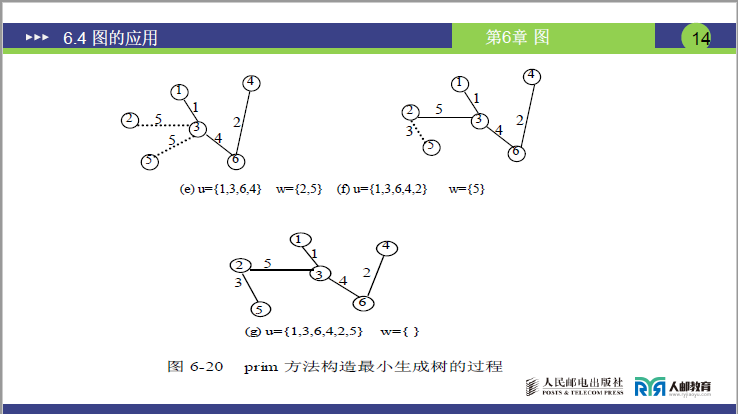
步骤 4：第三次选边与扩展（课件图 6-20（e））

选最短边：U-W间最小权边是 6-4（权 2），改实线；
扩展U：将 4 加入U，U={1,3,6,4}，W={2,5}；
修正边权：基于新加入的 4，检查U-W边：
- 4-2（∞）＞3-2（5）→ 保留 3-2（5）；
- 4-5（∞）＞3-5（5）→ 保留 3-5（5）；
- 无更新，直接保留原有虚线；

结果：生成树新增边 6-4，共 3 条边。

步骤 5：第四次选边与扩展（课件图 6-20（f））

选最短边：U-W间最小权边是 3-2（权 5），改实线；
扩展U：将 2 加入U，U={1,3,6,4,2}，W={5}；
修正边权：基于新加入的 2，更新U-W边权：
- 2-5（3）＜3-5（5）→ 删 3-5（5），改虚线 2-5（3）；

结果：生成树新增边 3-2，共 4 条边。

步骤 6：第五次选边与终止（课件图 6-20（g））

选最短边：U-W间仅存虚线 2-5（权 3），改实线；
扩展U：将 5 加入U，U={1,3,6,4,2,5}=V，W=空；
终止条件满足，生成树构建完成；

最终生成树边集：1-3（1）、3-6（4）、6-4（2）、3-2（5）、2-5（3）；
总权和：1+4+2+5+3=15（最小权和）。

（3）算法规律与学习提示

步骤数规律：n个顶点需n-1次选边（生成树边数），加 1 次初始化，共n步（如 6 个顶点，5 次选边 + 1 次初始化 = 6 步）；
核心逻辑：始终围绕 “U扩展”，每次选 “U-W 最短边”，保证生成树权和最小（贪心思想）；
画图技巧：初始化用虚线，选边后变实线，修正边权时 “只换更小的，不换更大的”；
考试重点：掌握算法思想（集合变化、选边逻辑），能手动模拟小案例（如 3-5 个顶点的网），无需死记代码（第二遍课程再讲实现）。

6.4.3克鲁斯卡尔（Kruskal）算法：边排序法

（1）算法基本思想

排序边：将图中所有边按权值递增顺序排列（需依赖排序算法，后续第八章详细讲解）；
选边判回路：依次选取权值最小的边，若该边与已选边不构成回路，则保留该边；若构成回路，则丢弃该边，继续选下一条权值更大的边；
终止条件：对于含n个顶点的图，当选中n-1条边时，算法结束（n-1条无回路边可构成树，且权值和最小）。

（2）与普里姆算法的区别

对比维度	普里姆算法	克鲁斯卡尔算法
扩展思路	按顶点扩展（`U`逐步扩大）	按边扩展（选排序后的边）
适合图类型	稠密图（边多，顶点少）	稀疏图（边少，顶点多）
核心难点	修正`U-W`边权	判断边是否形成回路（需并查集）

（3）算法执行步骤（结合课件图 6-22 示例）

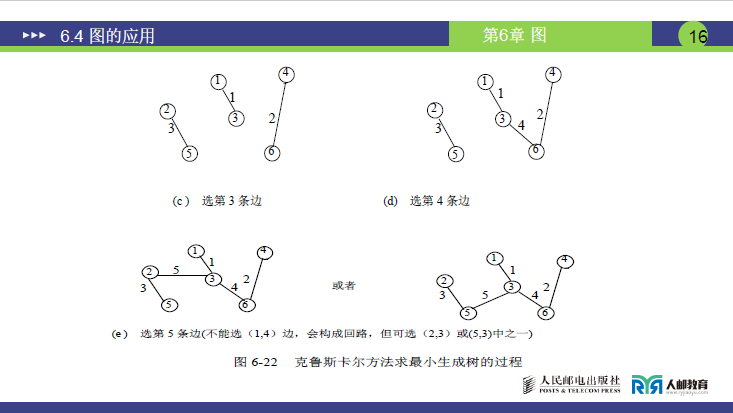
课件以 “图 6-20 (a) 中的无向网” 为示例（含 6 个顶点，需选 5 条边），具体选边过程如下（对应图 6-22 (a)-(e)，课件页码 15-16）：

步骤	选边操作	权值	是否构成回路	已选边集合（边：权值）	备注
1	选边 (1,3)	1	否（初始无已选边）		所有边中权值最小的边（对应图 6-22 (a)）
2	选边 (2,6)	2	否（与 (1,3) 无公共顶点，无回路）		剩余边中权值最小的边（对应图 6-22 (b)）
3	选边 (3,5)	3	否（与 (1,3) 公共顶点为 3，不构成回路）		剩余边中权值最小的边（对应图 6-22 (c)）
4	候选边 (1,4)	4	是（若选 (1,4)，1 与 4 无已选边连接？此处需结合原图：实际 (1,4) 会与 (1,3)、(3,5) 等构成回路，故丢弃）	不变	丢弃后选下一条权值为 5 的边（对应图 6-22 (d)）
5	选边 (2,3) 或 (5,3)	5	否（选 (2,3)：与 (2,6) 公共顶点 2、与 (1,3) 公共顶点 3，无回路；选 (5,3)：与 (3,5) 重复，故任选其一）		此时已选 4 条边，需再选 1 条（对应图 6-22 (e)）
6	选最后一条权值合适的边（如 (4,6)，权值 4？需结合原图，最终凑够 5 条边）	-	否	共 5 条边，满足 n-1（6-1=5）	算法结束，得到最小生成树

（4）关键说明

回路判断核心：选边时需检查 “边的两个顶点是否已在同一连通分量中”（后续可通过 “并查集” 数据结构高效实现，本节课暂不展开）；
与普里姆算法的区别：普里姆算法 “从顶点出发”（先选起始顶点，逐步扩展连通分量），克鲁斯卡尔算法 “从边出发”（先排序边，逐步选无回路边），前者更适合稠密图，后者更适合稀疏图；
最小性保证：因每次选权值最小的无回路边，最终n-1条边的权值和必然最小，符合最小生成树定义。

6.4.4 单源点最短路径

（1）单源点最短路径的定义

问题背景：在带权有向网G=(V,E)中，给定一个 “源点”（出发点）v₁，求v₁到其他所有顶点的最短路径（路径上各边权值之和最小，而非边数最少）；
关键前提：边的权值非负；若两顶点无直接边，初始距离设为∞（表示无直接通路，可能通过中转顶点到达）；
应用场景：交通网络中 “从某一城市到其他所有城市的最短距离 / 时间 / 费用” 计算。

（2）迪杰斯特拉（Dijkstra）算法 —— 单源点最短路径的核心解法

①算法基本思想

算法通过 “逐步扩充已确定最短路径的顶点集合” 实现，核心是两个集合的操作：

集合S：存放已求出最短路径的顶点（初始仅含源点v₁，v₁到自身的距离为 0）；
集合V-S（记为W）：存放未确定最短路径的顶点（初始含除v₁外的所有顶点，v₁到W中顶点的初始距离：有直接边则为边权，无直接边则为∞）。

算法步骤：

初始化S={v₁}，W=V-{v₁}，设置v₁到自身距离为 0，到W中顶点的初始距离；
从W中选一个 “v₁到其距离最小的顶点vₘ”，将vₘ加入S；
以vₘ为中转顶点，修正v₁到W中剩余顶点的距离：若v₁→vₘ的距离 + vₘ→vⱼ的距离 < v₁→vⱼ的当前距离，则更新v₁→vⱼ的距离为前者；
重复步骤 2-3，直到S=V（W为空），此时v₁到所有顶点的最短路径均已确定。

②算法执行步骤（结合课件图 6-27 示例）

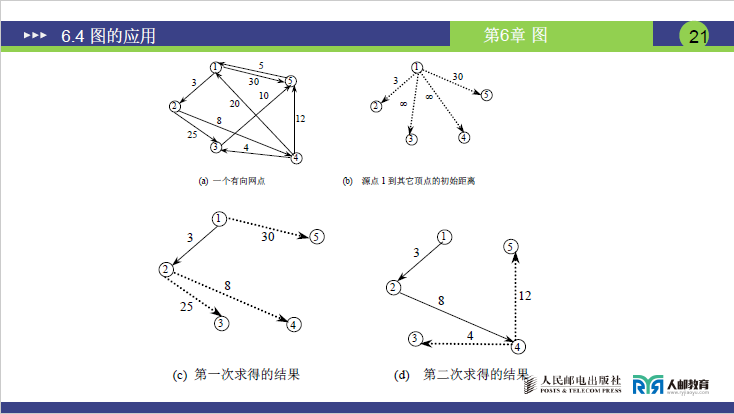
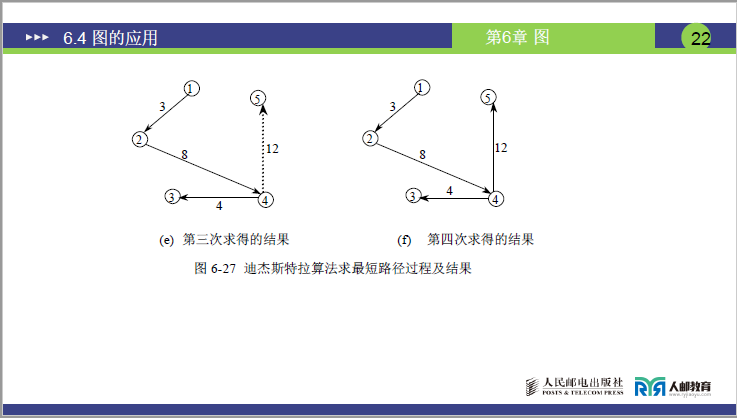
课件以 “图 6-27 (a) 的有向网” 为示例（源点为顶点 1，共 5 个顶点：1、2、3、4、5），具体执行过程如下（对应图 6-27 (a)-(f)，课件页码 19-22）：

A. 初始状态（对应图 6-27 (a)、(b)）

源点v₁=1，S={1}，W={2,3,4,5}；
初始距离（1到各顶点的距离）：
- 1→1：0（已确定）；
- 1→2：3（有直接边，边权 3）；
- 1→3：∞（无直接边）；
- 1→4：∞（无直接边，注意：有向网中 “4→1” 有边，但 “1→4” 无边）；
- 1→5：30（有直接边，边权 30）。

B.第一次迭代（对应图 6-27 (c)）

从W={2,3,4,5}中选距离最小的顶点：2（距离 3），将2加入S，此时S={1,2}，W={3,4,5}；
以2为中转顶点，修正1到W中顶点的距离：
- 1→3：原距离∞，中转后1→2（3） + 2→3（25）= 28 < ∞，故更新为 28；
- 1→4：原距离∞，中转后1→2（3） + 2→4（8）= 11 < ∞，故更新为 11；
- 1→5：原距离 30，中转后1→2（3） + 2→5（∞）= ∞ > 30，不更新；
此时1到W中顶点的距离：3→28、4→11、5→30（对应图 6-27 (c)）。

C.第二次迭代（对应图 6-27 (d)）

从W={3,4,5}中选距离最小的顶点：4（距离 11），将4加入S，此时S={1,2,4}，W={3,5}；
以4为中转顶点，修正1到W中顶点的距离：
- 1→3：原距离 28，中转后1→4（11） + 4→3（4）= 15 < 28，故更新为 15；
- 1→5：原距离 30，中转后1→4（11） + 4→5（12）= 23 < 30，故更新为 23；
此时1到W中顶点的距离：3→15、5→23（对应图 6-27 (d)）。

D.第三次迭代（对应图 6-27 (e)）

从W={3,5}中选距离最小的顶点：3（距离 15），将3加入S，此时S={1,2,4,3}，W={5}；
以3为中转顶点，修正1到5的距离：
- 1→5：原距离 23，中转后1→3（15） + 3→5（10）= 25 > 23，不更新；
此时1到5的距离仍为 23（对应图 6-27 (e)）。

E.第四次迭代（对应图 6-27 (f)）

从W={5}中选唯一顶点5（距离 23），将5加入S，此时S={1,2,4,3,5}（W为空）；
无剩余顶点需修正，算法结束。

F.最终结果（源点 1 到各顶点的最短路径）

源点→顶点	最短路径	路径权值和（最短距离）
1→1	1	0
1→2	1→2	3
1→3	1→2→4→3	3+8+4=15
1→4	1→2→4	3+8=11
1→5	1→2→4→5	3+8+12=23

（3）关键说明

与最小生成树的区分技巧：
- 最小生成树：处理无向网，目标是选n-1条边使权值和最小（构成树）；
- 迪杰斯特拉算法：处理有向网，目标是求 “单源点到所有顶点的最短路径”（非树结构，是路径集合）；
算法理解方法：强调 “跑例子”—— 通过手动模拟每一步选顶点、修正距离的过程，才能理解算法逻辑（避免死记硬背思想）；
时间复杂度：若用邻接矩阵存储图，每次选W中最小距离顶点需O(n)，修正距离需O(n)，共迭代n次，总时间复杂度为O(n²)。

所有顶点对之间的最短路径

问题定义
- 给定有向网G=(V,E)，对任意一对有序顶点(vᵢ, vⱼ)（i≠j），求vᵢ到vⱼ的最短距离，以及vⱼ到vᵢ的最短距离（需考虑有向边的方向）。
求解方法
- 方法 1：重复执行迪杰斯特拉算法n次
  - 思路：轮流将每个顶点作为 “源点”，对每个源点执行一次迪杰斯特拉算法，即可得到所有顶点对的最短路径；
  - 时间复杂度：每次迪杰斯特拉算法时间复杂度为O(n²)，重复n次后，总时间复杂度为O(n³)；
  - 适用场景：边权非负的有向网（迪杰斯特拉算法不支持负权边）。
- 方法 2：弗洛伊德（Floyd）算法
  - 思路：通过 “动态规划” 思想，引入 “中转顶点k”，逐步更新vᵢ到vⱼ的最短距离（d[i][j] = min(d[i][j], d[i][k] + d[k][j])），直接在距离矩阵上进行变换；
  - 时间复杂度：O(n³)（与方法 1 相同，但实现更简洁，且支持负权边，不支持负权回路）；
  - 优势：无需重复调用迪杰斯特拉算法，一次遍历即可得到所有顶点对的最短路径。
- 关键说明
  - 两种方法的时间复杂度均为O(n³)，但弗洛伊德算法的代码实现更简洁，且对负权边的兼容性更好（需注意无负权回路）；
  - 应用场景：当需要一次性求所有顶点对的最短路径时（如交通网络中 “所有城市间的最短路线表”），优先选择弗洛伊德算法；若仅需单源点路径，迪杰斯特拉算法更高效。

6.4.5 拓扑排序（课件 P24-30）

拓扑排序是图的重要应用之一，核心解决 “有先后依赖关系的活动如何有序执行” 的问题，广泛用于工程调度、课程安排等场景。

（1）拓扑排序的引入

在实际场景中，许多活动存在先后依赖关系：

工程场景：大工程拆分为多个子活动（如 “设计图纸” 需在 “施工” 前完成），需按依赖关系有序执行才能高效完成。
课程安排场景（讲课重点示例）：计算机专业课程开设存在 “先修 - 后继” 关系（如 “数据结构” 需先学 “程序设计基础” 和 “离散数学”），不能随意安排顺序。

拓扑排序的本质就是：将存在依赖关系的活动（顶点）排列成一个线性序列，确保所有前驱活动先执行、后继活动后执行。

（2）AOV 网：拓扑排序的载体

为了描述活动的依赖关系，引入AOV 网（顶点表示活动的网络，Activity On Vertices），其定义与性质如下：

核心要素	定义
顶点（Vertex）	表示一个 “活动”（如课程 “高等数学”、“数据结构”）
有向边（Edge）	表示活动的 “优先关系”：若存在有向边`<<i,j>`，则活动`i`是活动`j`的直接前驱，活动`j`是活动`i`的直接后继（即`i`必须完成后，`j`才能开始）
关键性质	1. 传递性：若`i`是`j`的前驱，`j`是`k`的前驱，则`i`是`k`的前驱；2. 反自反性：任何活动不能以自身为前驱 / 后继；3. 无环性：AOV 网中不能存在有向环（否则会出现 “活动 A 依赖 B，B 依赖 A” 的矛盾，工程无法进行）

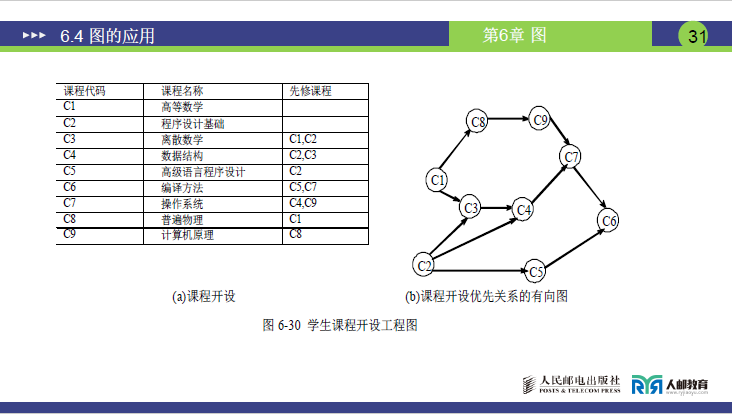
示例：计算机专业课程的 AOV 网

课件中给出计算机专业核心课程的 “先修关系表” 及对应的 AOV 网，具体如下：

课程先修关系表（讲课详细解读）：

课程代号	课程名称	先修课程（直接前驱）	解读（讲课补充）
C1	高等数学	无	无先修课，可最早开设
C2	程序设计基础	无	无先修课，可最早开设
C3	离散数学	C1、C2	需先学 “高等数学（C1）” 和 “程序设计基础（C2）”
C4	数据结构	C2、C3	需先学 “程序设计基础（C2）” 和 “离散数学（C3）”
C5	高级语言程序设计	C2	需先学 “程序设计基础（C2）”
C6	编译原理	C5、C7	计算机四大王牌课之一，需先学 “高级语言（C5）” 和 “操作系统（C7）”
C7	操作系统	C4、C9	需先学 “数据结构（C4）” 和 “普通物理（C9）”
C8	计算机原理	C1	需先学 “高等数学（C1）”
C9	普通物理	C1	需先学 “高等数学（C1）”

对应的 AOV 网（图 6-30（b））：
- 顶点：C1~C9（9 门课程，即 9 个活动）；
- 有向边：<C1,C3>（C1 是 C3 的先修）、<C2,C3>（C2 是 C3 的先修）、<C3,C4>（C3 是 C4 的先修）等，完全体现先修关系。

（3）拓扑排序的算法步骤

拓扑排序的核心是 “反复找入度为 0 的顶点（无未完成的前驱活动），删除其及出边”，具体步骤如下：

选顶点：在 AOV 网中选择一个入度为 0的顶点（无任何前驱活动未完成），将其输出到拓扑序列中；
删边：从 AOV 网中删除该顶点，以及所有从该顶点出发的有向边（这些边对应的后继活动的 “前驱依赖” 已满足）；
循环终止：重复步骤 1 和 2，直到以下两种情况之一：
- 情况 1：AOV 网中所有顶点都被输出 → 拓扑排序成功，AOV 网无环（工程可正常执行）；
- 情况 2：网中无入度为 0 的顶点，但仍有顶点未输出 → 拓扑排序失败，AOV 网存在有向环（工程无法执行）。

（4）拓扑排序示例

示例 1：计算机课程 AOV 网的拓扑排序（讲课详细推导）

以图 6-30（b）的课程 AOV 网为例，逐步执行拓扑排序：

初始状态：入度为 0 的顶点是C1（高等数学）、C2（程序设计基础）（无先修课）；
- 输出 C1 → 删除 C1 的出边<C1,C3>、<C1,C8>、<C1,C9>；
- 此时入度为 0 的顶点：C2（入度仍 0）、C8（删除<C1,C8>后入度 0）、C9（删除<C1,C9>后入度 0）。
输出 C2 → 删除 C2 的出边<C2,C3>、<C2,C4>、<C2,C5>；
- 此时入度为 0 的顶点：C3（删除<C1,C3>和<C2,C3>后入度 0）、C8、C9。
输出 C8 → 无出边（C8 无后继课程），直接删除；
- 输出 C9 → 删除 C9 的出边<C9,C7>；
- 此时入度为 0 的顶点：C3、C5（删除<C2,C5>后入度 0）。
输出 C3 → 删除 C3 的出边<C3,C4>；
- 输出 C5 → 删除 C5 的出边<C5,C6>；
- 此时入度为 0 的顶点：C4（删除<C2,C4>和<C3,C4>后入度 0）。
输出 C4 → 删除 C4 的出边<C4,C7>；
- 此时入度为 0 的顶点：C7（删除<C4,C7>和<C9,C7>后入度 0）。
输出 C7 → 删除 C7 的出边<C7,C6>；
- 此时入度为 0 的顶点：C6（删除<C5,C6>和<C7,C6>后入度 0）。
输出 C6 → 所有顶点输出完毕。
- 最终拓扑序列（一种可能）：C1→C2→C8→C9→C3→C5→C4→C7→C6（序列不唯一，只要满足依赖关系即可）。

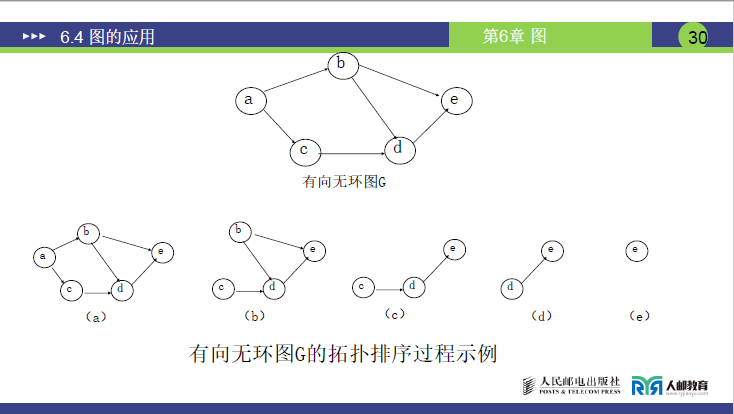
示例 2：有向无环图 G 的拓扑排序（课件 P30 图）

课件给出一个简单有向无环图 G（顶点 a、b、c、d、e），拓扑排序过程如下：

初始入度为 0 的顶点：a（无入边）；
- 输出 a → 删除 a 的出边<a,b>、<a,c>（图 6-30（a）→（b））；
- 入度为 0 的顶点：b、c。
输出 b → 删除 b 的出边<b,d>（图 6-30（b）→（c））；
- 入度为 0 的顶点：c。
输出 c → 删除 c 的出边<c,d>（图 6-30（c）→（d））；
- 入度为 0 的顶点：d。
输出 d → 删除 d 的出边<<d,e>（图 6-30（d）→（e））；
- 入度为 0 的顶点：e。
输出 e → 所有顶点输出完毕，排序成功（序列：a→b→c→d→e）。

（5）拓扑排序的核心作用

生成合法活动序列：为有依赖关系的活动（如课程、工程子任务）提供可执行的顺序；
判断 AOV 网是否有环：若排序后仍有顶点未输出，说明网中存在有向环（如 “课程 A 依赖 B，B 依赖 C，C 依赖 A”，三者无法开设），工程 / 任务无法执行。

6.4.6 关键路径（对应课件 34-42 页）

（1） AOE 网的定义与核心特征

① AOE 网的定义

全称：Activity On Edge Network（活动在边的网），是一种带权有向图，具体定义为：
- 顶点（Vertex）：代表事件（Event），即工程进展中的某个状态（如 “开工”“地基完成”“竣工”），事件是瞬间发生的（无持续时间）。
- 弧（Arc）：代表活动（Activity），即实现事件转换的具体任务（如 “地基施工”“墙体砌筑”）。
- 弧的权值（Weight）：代表完成该活动所需的时间（如 “地基施工需 10 天”）。

②AOE 网的核心特征

源点唯一：入度为 0 的顶点（工程开始事件，如 “项目开工日”），整个工程仅一个起点。
汇点唯一：出度为 0 的顶点（工程结束事件，如 “项目竣工日”），整个工程仅一个终点。
无环：若有环，活动循环依赖，工程无法推进（需通过拓扑排序验证）。

③AOE 网实例解析

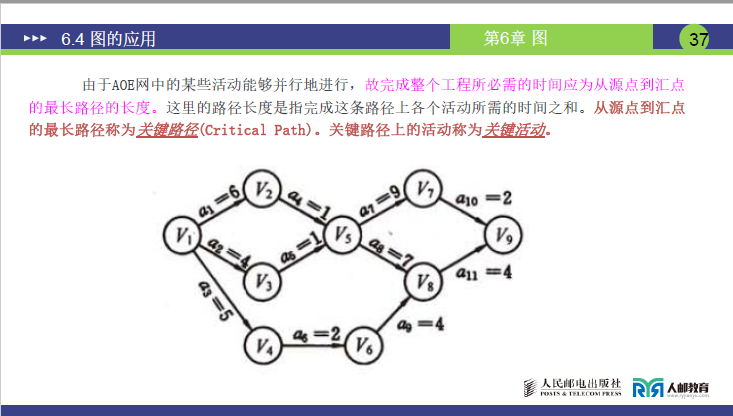
实例规模：9 个事件（V₁~V₉）、11 个活动（a₁~a₁₁），各活动时间及事件含义如下：

事件	含义（对应老师讲课解释）	关联活动（入弧：已完成活动；出弧：可开始活动）
V₁	工程开始（源点，入度 0）	出弧：a₁（V₁→V₂，6 天）、a₂（V₁→V₃，4 天）、a₃（V₁→V₄，5 天）
V₂	a₁完成，a₄可开始	入弧：a₁；出弧：a₄（V₂→V₅，1 天）
V₃	a₂完成，a₅可开始	入弧：a₂；出弧：a₅（V₃→V₅，1 天）
V₄	a₃完成，a₆可开始	入弧：a₃；出弧：a₆（V₄→V₆，2 天）
V₅	a₄、a₅完成，a₇、a₈可开始	入弧：a₄、a₅；出弧：a₇（V₅→V₇，9 天）、a₈（V₅→V₈，7 天）
V₆	a₆完成，a₉可开始	入弧：a₆；出弧：a₉（V₆→V₈，4 天）
V₇	a₇完成，a₁₀可开始	入弧：a₇；出弧：a₁₀（V₇→V₉，2 天）
V₈	a₈、a₉完成，a₁₁可开始	入弧：a₈、a₉；出弧：a₁₁（V₈→V₉，4 天）
V₉	工程结束（汇点，出度 0）	入弧：a₁₀、a₁₁

举例：事件 V₅类似 “交作业前需完成‘写作业’（a₄）和‘买作业本’（a₅）”，只有这两个活动都完成，才能开始 “交作业”（a₇、a₈）相关活动。

（2）关键路径相关核心概念

为明确关键路径的判定依据，需先掌握以下概念：

概念	教材定义（课件 36 页）	通俗解释（更易理解应用）
源点	整个工程开始时的顶点（入度为 0）	工程开工日（如建大楼的 “奠基日”），无任何前置任务。
汇点	整个工程结束时的顶点（出度为 0）	工程竣工日（如建大楼的 “验收通过日”），所有任务最终汇总于此。
路径	由源点经一系列顶点到达汇点的有向边（活动）组成的序列	工程的一条执行流程（如 “开工→地基→主体→竣工”）。
路径长度	路径上所有活动的时间之和	完成某条流程所需的总时间（如 “地基 10 天 + 主体 20 天 = 30 天”）。
最长路径长度	所有路径中长度最大的数值	工程最少完成时间（因并行活动需等最慢的流程完成，如 “地基 10 天、水电 8 天，需等地基完成才进主体”）。
关键活动	不按期完成则整个工程无法按期完成的活动	“牵一发而动全身” 的活动（如 “主体建设延误 1 天，竣工必延误 1 天”）。
关键路径	从源点到汇点的最长路径；关键路径上的活动为关键活动（教材定义，课件 37 页）	关键活动连接而成的路径（老师定义，更实用）；如 “a₁→a₄→a₇→a₁₀”“a₁→a₄→a₈→a₁₁”。

强调：教材 “最长路径 = 关键路径” 的定义仅用于理论判定，实际求解需通过 “找关键活动→连关键路径” 的方式（即五变量法），更易操作。

（3）关键路径求解：五变量法

核心思路：通过计算 5 个变量，判断每个活动的 “时间余量”（松弛时间），无余量的活动即为关键活动，进而构成关键路径。以下为变量定义、公式及实例计算。

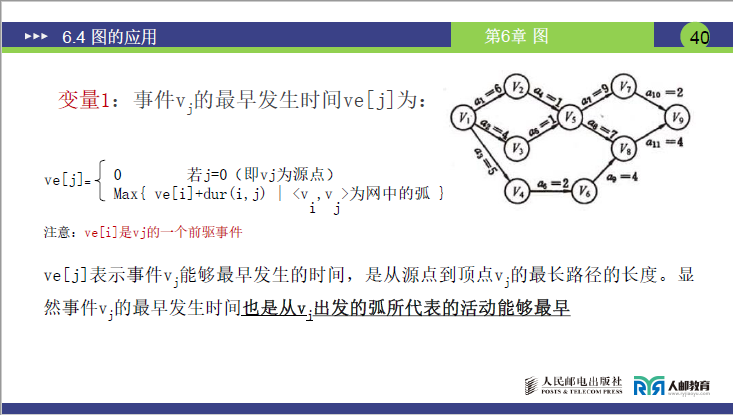
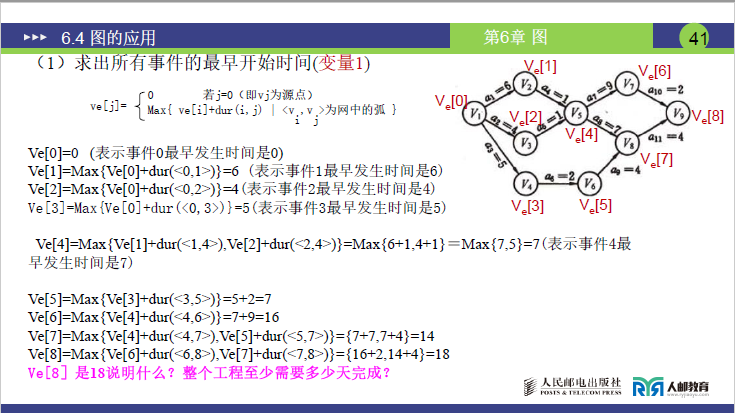
变量 1：事件的最早发生时间（Ve [j]）——“事件最早能在第几天发生”

定义（课件 38 页）：事件 Vⱼ最早发生的时间，等于从源点到 Vⱼ的最长路径长度（需等所有前置活动完成，取最慢的流程时间）。
公式（课件 40 页）：

\[Ve[j] = \begin{cases} 0 & \text{若 } j=0 (V_j \text{为源点，对应课件35页} V_1 ) \\ \text{Max}\{Ve[i] + dur(i, j) \mid <V_i, V_j> \text{为网中的弧} \} & \text{其他情况} \end{cases} \]
- 说明：dur(i,j) 是活动 <V_i,V_j> 的持续时间；Ve[i] 是 Vⱼ的前驱事件 Vᵢ的最早发生时间。
实例计算（对应课件 40-41 页，事件编号按课件 0~8 对应 V₁~V₉）：
- Ve [0]（V₁，源点）= 0（公式规定）
- Ve [1]（V₂）= Max {Ve [0] + dur (0,1)} = 0 + 6 = 6（仅 1 条前置路径：V₁→V₂）
- Ve [2]（V₃）= Max {Ve [0] + dur (0,2)} = 0 + 4 = 4（仅 1 条前置路径：V₁→V₃）
- Ve [3]（V₄）= Max {Ve [0] + dur (0,3)} = 0 + 5 = 5（仅 1 条前置路径：V₁→V₄）
- Ve [4]（V₅）= Max {Ve [1]+dur (1,4), Ve [2]+dur (2,4)} = Max {6+1, 4+1} = Max {7,5} = 7（2 条前置路径：V₂→V₅、V₃→V₅，取最长）
- Ve [5]（V₆）= Max {Ve [3] + dur (3,5)} = 5 + 2 = 7（仅 1 条前置路径：V₄→V₆）
- Ve [6]（V₇）= Max {Ve [4] + dur (4,6)} = 7 + 9 = 16（仅 1 条前置路径：V₅→V₇）
- Ve [7]（V₈）= Max {Ve [4]+dur (4,7), Ve [5]+dur (5,7)} = Max {7+7, 7+4} = Max {14,11} = 14（2 条前置路径：V₅→V₈、V₆→V₈，取最长）
- Ve [8]（V₉，汇点）= Max {Ve [6]+dur (6,8), Ve [7]+dur (7,8)} = Max {16+2, 14+4} = Max {18,18} = 18
关键结论：汇点 Ve [8]=18，即整个工程最少需 18 天完成（强调：考试中求工程最少时间，直接算汇点的 Ve 值即可）。

变量 2：事件的最晚发生时间（Vl [j]）——“事件最晚能在第几天发生，且不延误工期”

定义（课件 38 页）：事件 Vⱼ最晚发生的时间，需保证后续活动能在工程最少时间内完成（即不影响汇点的最早发生时间）。
公式（课件 43 页）：

\[Vl[j] = \begin{cases} Ve[n-1] & \text{若 } j=n-1 (V_j \text{为汇点， } n \text{为事件总数}) \\ \text{Min}\{Vl[k] - dur(j, k) \mid <V_j, V_k> \text{ 为网中的弧} \} & \text{其他情况} \end{cases} \]
- 说明：Vl[k] 是 Vⱼ的后继事件 Vₖ的最晚发生时间；需取 Min 是为了避免后续活动时间不足（如 “后续活动最晚需 18 天完成，若本事件太晚，后续活动无法按时结束”）。
实例计算（对应课件 43 页，汇点 Vl [8]=Ve [8]=18，逆序计算）：
- Vl [8]（V₉，汇点）= Ve [8] = 18（公式规定，工期不延误，汇点最晚与最早发生时间一致）
- Vl [7]（V₈）= Min {Vl [8] - dur (7,8)} = 18 - 4 = 14（仅 1 条后继路径：V₈→V₉）
- Vl [6]（V₇）= Min {Vl [8] - dur (6,8)} = 18 - 2 = 16（仅 1 条后继路径：V₇→V₉）
- Vl [5]（V₆）= Min {Vl [7] - dur (5,7)} = 14 - 4 = 10（仅 1 条后继路径：V₆→V₈）
- Vl [4]（V₅）= Min {Vl [6]-dur (4,6), Vl [7]-dur (4,7)} = Min {16-9, 14-7} = Min {7,7} = 7（2 条后继路径：V₅→V₇、V₅→V₈，取最小）
- Vl [3]（V₄）= Min {Vl [5] - dur (3,5)} = 10 - 2 = 8（仅 1 条后继路径：V₄→V₆）
- Vl [2]（V₃）= Min {Vl [4] - dur (2,4)} = 7 - 1 = 6（仅 1 条后继路径：V₃→V₅）
- Vl [1]（V₂）= Min {Vl [4] - dur (1,4)} = 7 - 1 = 6（仅 1 条后继路径：V₂→V₅）
- Vl [0]（V₁，源点）= Min {Vl [1]-dur (0,1), Vl [2]-dur (0,2), Vl [3]-dur (0,3)} = Min {6-6, 6-4, 8-5} = Min {0,2,3} = 0
举例：事件 V₃（Vl [2]=6）的含义是 “V₃最晚需在第 6 天发生，若超过 6 天，后续活动 V₃→V₅（1 天）完成时间会超过 V₅的最晚发生时间 7 天，导致工期延误”。

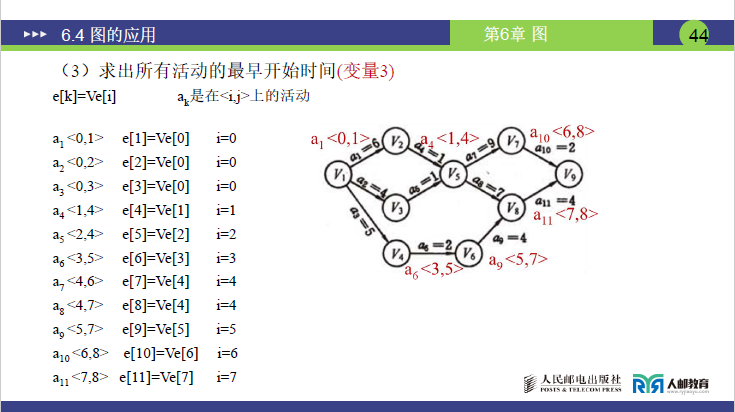
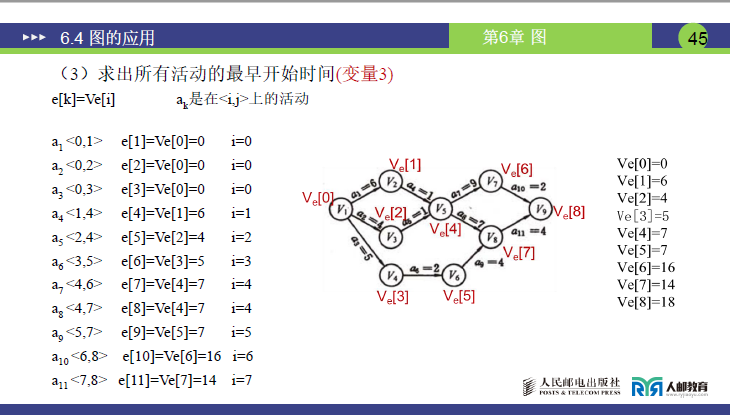
变量 3：活动的最早开始时间（e [k]）——“活动最早能在第几天开始”

定义（课件 38 页）：活动 aₖ（对应弧<V_i,V_j>）的最早开始时间，等于其起点事件 Vᵢ的最早发生时间（Vᵢ发生后，活动即可开始）。
公式（课件 44-45 页）：e[k]=Ve[i]（aₖ对应弧<V_i,V_j>，i 为起点事件编号）

实例计算（对应课件 45 页，11 个活动）：

活动	对应弧	e [k] = Ve [i]（i 为起点事件编号）	计算结果
a₁	<0,1>（V₁→V₂）	Ve[0]	0
a₂	<0,2>（V₁→V₃）	Ve[0]	0
a₃	<0,3>（V₁→V₄）	Ve[0]	0
a₄	<1,4>（V₂→V₅）	Ve[1]	6
a₅	<2,4>（V₃→V₅）	Ve[2]	4
a₆	❤️,5>（V₄→V₆）	Ve[3]	5
a₇	<4,6>（V₅→V₇）	Ve[4]	7
a₈	<4,7>（V₅→V₈）	Ve[4]	7
a₉	<5,7>（V₆→V₈）	Ve[5]	7
a₁₀	<6,8>（V₇→V₉）	Ve[6]	16
a₁₁	<7,8>（V₈→V₉）	Ve[7]	14

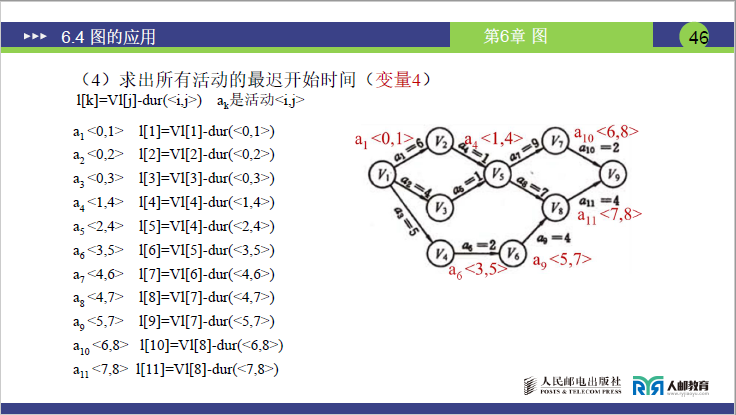
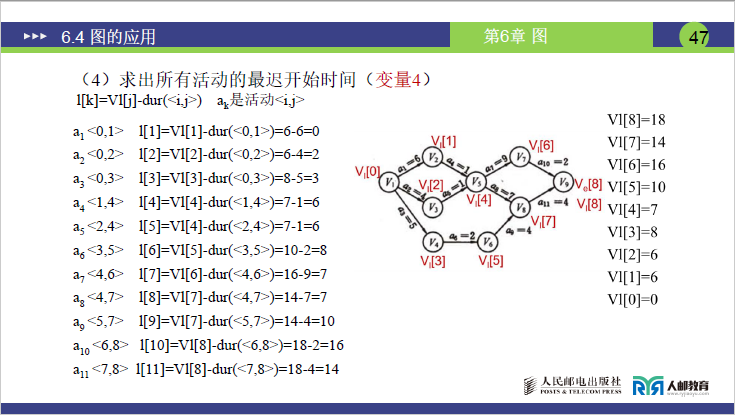
变量 4：活动的最晚开始时间（l [k]）——“活动最晚能在第几天开始，且不延误工期”

定义（课件 38 页）：活动 aₖ（对应弧<V_i,V_j>）的最晚开始时间，需保证其终点事件 Vⱼ能在最晚时间发生（即 Vⱼ的 Vl [j] 减去活动持续时间）。
公式（课件 46 页）：l[k]=Vl[j]−dur(i,j)（aₖ对应弧<V_i,V_j>，j 为终点事件编号，dur (i,j) 为活动时间）

实例计算（对应课件 46-47 页，11 个活动）：

活动	对应弧	l [k] = Vl [j] - dur (i,j)（j 为终点编号，dur 为活动时间）	计算结果
a₁	<0,1>（V₁→V₂）	Vl[1] - 6（dur=6）	6-6=0
a₂	<0,2>（V₁→V₃）	Vl[2] - 4（dur=4）	6-4=2
a₃	<0,3>（V₁→V₄）	Vl[3] - 5（dur=5）	8-5=3
a₄	<1,4>（V₂→V₅）	Vl[4] - 1（dur=1）	7-1=6
a₅	<2,4>（V₃→V₅）	Vl[4] - 1（dur=1）	7-1=6
a₆	❤️,5>（V₄→V₆）	Vl[5] - 2（dur=2）	10-2=8
a₇	<4,6>（V₅→V₇）	Vl[6] - 9（dur=9）	16-9=7
a₈	<4,7>（V₅→V₈）	Vl[7] - 7（dur=7）	14-7=7
a₉	<5,7>（V₆→V₈）	Vl[7] - 4（dur=4）	14-4=10
a₁₀	<6,8>（V₇→V₉）	Vl[8] - 2（dur=2）	18-2=16
a₁₁	<7,8>（V₈→V₉）	Vl[8] - 4（dur=4）	18-4=14

变量 5：松弛时间（Slack Time）——“活动的时间余量”

定义（课件 39 页）：活动 aₖ的时间余量，即最晚开始时间与最早开始时间的差值，公式为：松弛时间=l[k]−e[k]。
核心判断规则（课件 39 页）：
- 若松弛时间 = 0：活动无时间余量，延误则工期延误→关键活动。
- 若松弛时间 > 0：活动有时间余量，延误不影响工期→非关键活动。

实例计算（11 个活动的松弛时间与关键活动判定）：

活动	e[k]	l[k]	松弛时间 = l [k]-e [k]	是否为关键活动
a₁	0	0	0	是
a₂	0	2	2	否
a₃	0	3	3	否
a₄	6	6	0	是
a₅	4	6	2	否
a₆	5	8	3	否
a₇	7	7	0	是
a₈	7	7	0	是
a₉	7	10	3	否
a₁₀	16	16	0	是
a₁₁	14	14	0	是

（4）关键路径最终确定

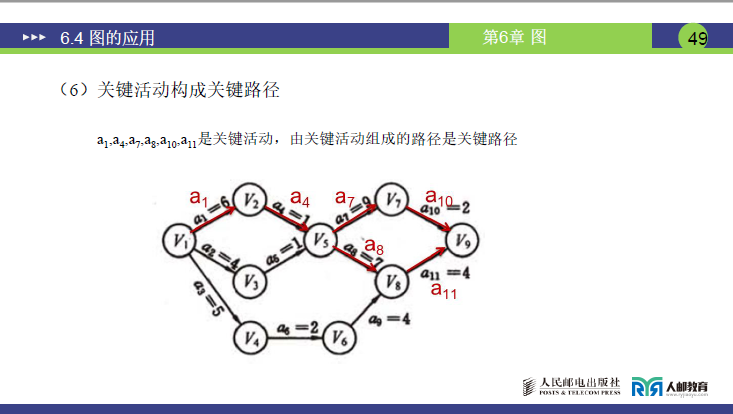
1.关键路径定义

由关键活动首尾连接形成的路径（即无时间冗余的活动构成的路径），对应课件 49 页的 AOE 网图中红色标注的路径。

2.关键路径示例（结合课件 49 页图）

根据关键活动a1、a4、a7、a8、a10、a11，可构成两条关键路径：

\(v_0 \xrightarrow{a_1} v_1 \xrightarrow{a_4} v_4 \xrightarrow{a_7} v_6 \xrightarrow{a_{10}} v_8 \quad (\text{路径长度: } 6+1+9+2=18) ;\)
\(v_0 \xrightarrow{a_1} v_1 \xrightarrow{a_4} v_4 \xrightarrow{a_7} v_6 \xrightarrow{a_{10}} v_8 \quad (\text{路径长度: } 6+1+7+4=18) ;\)。

3.关键路径意义

关键路径的长度 = 总工期（18 天），是源点到汇点的最长路径；
关键活动是 “瓶颈”：任何关键活动延误 1 天，总工期必延误 1 天；
非关键活动有冗余：如a2可延误 2 天，a3可延误 3 天，不影响总工期。

（5）关键路径求解总结

完整的关键路径求解需分 4 步，确保无环（若拓扑排序无法输出所有顶点，说明网中有环，工程无法完成）：

步骤 1：拓扑排序：对 AOE 网进行拓扑排序，得到拓扑序列（如v0→v1→v2→v3→v4→v5→v6→v7→v8）；
步骤 2：计算事件最早发生时间Ve(j)：按拓扑序列从源点到汇点，依次计算每个事件的Ve(j)（用 max）；
步骤 3：计算事件最迟发生时间Vl(j)：按逆拓扑序列从汇点到源点，依次计算每个事件的Vl(j)（用 min）；
步骤 4：判断关键活动与关键路径：对每个活动a_k=<<i,j>，若e[k]=l[k]（即Ve(i)+dur(i,j)=Vl(j)），则为关键活动；将关键活动连接成关键路径。

总结

关键路径的核心是 “找无时间冗余的活动”，依赖 5 个变量的逐步计算；
总工期由汇点的Ve(n−1)决定，关键活动延误则总工期延误；
求解前需先拓扑排序，避免网中有环导致工程无法推进。

参考资料：教材《数据结构 C 语言第 3 版》数据结构考研指导（基础篇）、数据结构考研指导（基础篇）视频课程｜赵海英

posted @ 2025-12-16 15:51 CodeMagicianT 阅读(26) 评论(0) 收藏举报

刷新页面返回顶部

codemagiciant

代码自由

第6章 图

第6章 图

6.1 图的定义和基本数据

6.1.1 图的定义

（1）图的核心定义

（2）无向图与有向图的定义及二元组表示

6.1.2 图的基本术语

（1）有向图与无向图（基础分类）

（2）完全图、稠密图、稀疏图

①完全图

②一般图的边 / 弧数范围

③稠密图与稀疏图

（3）度、入度、出度

①度的通用定义

②有向图的入度与出度

③无向图的度

④典型问题：特殊有向图的形状

（4）连通图与强连通图

（5）网

（6）子图

6.2 图的存储结构

6.2.1 邻接矩阵（顺序存储，底层为二维数组）

（1）邻接矩阵的定义

（2）不同类型图的邻接矩阵表示

①无向图的邻接矩阵

②有向图的邻接矩阵

结论

③网的邻接矩阵（带权图）

（3）邻接矩阵的优缺点（扩展补充）

6.2.2 邻接表（链式存储，头节点 + 表节点）

（1）邻接表的存储结构（课件定义）

（2）不同类型图的邻接表表示

①无向图的邻接表

②有向图的邻接表与逆邻接表

③网的邻接表

（3）邻接表的优缺点

6.2.3邻接矩阵与邻接表的核心对比

6.2.4讲课中的考试与学习注意事项

6.3 图的遍历

6.3.1图的遍历概述

（1）定义

（2）核心意义

（3）两种经典遍历方法

6.3.2 深度优先搜索（DFS）遍历

（1）算法核心思想

（2）算法执行步骤（标准流程）

（3）辅助存储结构

（4）典型示例（无向图 G7，从顶点 0 出发）

①图的背景

②以顶点 0 为起始点的遍历过程（讲课内容补充）

③遍历序列与唯一性分析

（5）关键结论与考点

6.3.3 广度优先搜索（BFS）遍历

（1）算法核心思想

（2）算法执行步骤（课件标准流程）

关键区别：与深度优先搜索的辅助结构对比

（3）辅助存储结构

（4）典型示例（无向图 G7，从顶点 1 出发）

①图的背景

②以顶点 1 为起始点的遍历过程（讲课内容补充）

③遍历序列与唯一性分析（课件页码 7）

（5）快速判断合法 BFS 序列的技巧

（6）两种遍历方法核心总结

6.4 图的应用

6.4.1. 生成树和最小生成树

（1）课程引入：图的核心应用方向

（2）生成树和最小生成树

①生成树的定义与本质

1. 课件核心定义

2. 图与树的区别

3. 生成树的构造方法（衔接图的遍历）

（3）最小生成树：带权图的 “最优” 生成树

①核心概念：从 “图” 到 “网”

②应用场景

③两种经典算法

6.4.2 普里姆（Prim）算法：顶点扩展法求 MST

（1）算法核心思想

①三大集合定义

第6章图

第6章图

②核心步骤（循环执行至`W`为空）

（2）实操示例：无向网（顶点 1-6）的 MST 构建（课件第 12-14 页图 6-20）

（3）关键路径求解：五变量法

（4）关键路径最终确定