第5章 树和二叉树

第5章 树和二叉树

复习回顾

核心目标：回顾线性表、栈和队列的学习逻辑，提炼数据结构通用学习方法，为后续第五章树、第六章图的学习铺垫

1. 第二板块整体章节框架

1. 第二板块章节构成

   本板块包含 4 章内容，分别为第 2 章、第 3 章、第 5 章、第 6 章。

   • 已学内容：第 2 章（线性表）、第 3 章（栈和队列）—— 均属于线性结构
   • 待学内容：第 5 章（树）、第 6 章（图）—— 均属于非线性结构，难度更高、地位更重要

2. 复习目的

   提炼线性结构的学习逻辑，迁移应用到后续非线性结构的学习中

2.第二章 线性表 核心知识点回顾

（1） 线性结构的核心特点（定义 + 判断依据）

线性结构有 4 个核心特点，这既是线性结构的定义，也是判断某一结构是否为线性结构的依据。

线性表是最简单的线性结构，是我们学习线性结构的切入点。

（2） 线性表的学习逻辑（通用学习步骤雏形）

强调：学习任何一种数据结构，都遵循 “定义 → 逻辑结构 → 存储结构 → 操作” 的核心流程，线性表的学习完美契合该流程：

1. 步骤 1：明确线性表的定义

   从线性结构中抽取的最简单结构，是具有相同数据类型的 n 个元素的有限序列。

2. 步骤 2：绘制逻辑结构（核心描述手段）

   逻辑结构描述数据元素之间的逻辑关系，线性表的逻辑关系是 “一对一”（除第一个和最后一个元素外，每个元素有且仅有一个直接前驱和一个直接后继）。

   课件 2 页右上角的图就是线性表的逻辑结构图，直观呈现元素的有序排列关系。

3. 步骤 3：定义存储结构（物理结构）

   • 强调：存储结构又叫物理结构，解决 “如何将数据结构存入计算机” 的问题。
   • 线性表的存储结构分为两种核心类型：顺序存储（顺序表）、链式存储（链表），后续需掌握两种存储结构的具体实现方式。

4. 步骤 4：掌握核心操作（算法实现）

   学习数据结构的最终目的是用算法解决实际问题，操作就是算法的具体步骤序列。

   线性表的常用操作包括：初始化、插入、删除、查找、遍历、销毁等，需结合不同存储结构理解操作的实现逻辑（如顺序表插入需移动元素，链表插入只需改变指针指向）。

3. 第三章 栈和队列 核心知识点回顾

（1） 栈和队列的引出逻辑

栈和队列是从线性表中抽取的两种最常用的线性结构，本质仍属于线性结构，逻辑关系同样是 “一对一”，因此逻辑结构部分讲解较少，重点聚焦特点和操作的特殊性。

（2） 栈和队列的通用学习步骤

与线性表一致，遵循 “定义 → 特点 → 逻辑结构 → 存储结构 → 操作” 的流程，且针对二者的特殊性做了对比学习：

1. 步骤 1：明确定义

   • 栈：限定仅在表尾进行插入和删除操作的线性表，表尾称为栈顶，表头称为栈底。
   • 队列：限定仅在表尾进行插入操作、在表头进行删除操作的线性表，表尾称为队尾，表头称为队头。

2. 步骤 2：对比核心特点（最关键区别）

   • 栈：后进先出（LIFO） —— 最后插入的元素最先被删除。

   • 队列：先进先出（FIFO）—— 最先插入的元素最先被删除。

     二者的操作端点差异：栈只有一个操作端（栈顶），队列有两个操作端（队头 + 队尾）。

3. 步骤 3：逻辑结构

   二者均为线性结构，逻辑关系是 “一对一”，因此无需额外讲解，可直接参考线性表的逻辑结构，重点关注操作端点的特殊性。

4. 步骤 4：存储结构

   与线性表一致，支持顺序存储和链式存储。需注意顺序存储时的特殊问题（如队列的假满）。

5. 步骤 5：核心操作（共 6 个，含优化逻辑）

   老师强调：栈和队列的操作均围绕 “判空、判满、插入、删除、初始化、销毁” 展开，共 6 个核心操作，具体细节有差异：

   • 栈的 6 个操作

     基础操作有 4 个：初始化、入栈（栈顶插入）、出栈（栈顶删除）、销毁；为了保证操作的合法性，补充 2 个操作：判空、判满 → 合计 6 个操作。

   • 队列的 6 个操作（循环队列优化）

     问题：顺序存储的普通队列会出现假满现象（队尾指针到达数组末端，但队头前方仍有空闲空间）。

     解决：使用循环队列（将顺序队列的存储空间想象成环形），不加说明时，队列默认指循环队列。

     循环队列的 6 个操作：初始化、入队（队尾插入）、出队（队头删除）、判空、判满、销毁。

4. 数据结构通用学习方法总结

（1） 通用学习四步法

从线性表、栈和队列的学习中，提炼出所有数据结构的通用学习流程，后续第五章树、第六章图的学习完全遵循该流程：

1. 第一步：明确定义

   掌握该数据结构的本质特征，区分与其他结构的核心差异。

2. 第二步：分析特点

   总结该结构的关键属性（如线性 / 非线性、操作限制等），这是后续学习的核心依据。

3. 第三步：绘制逻辑结构

   用图形直观展示数据元素之间的逻辑关系，这是理解结构的基础。

4. 第四步：定义存储结构 + 掌握核心操作

   • 存储结构：确定用顺序还是链式方式存入计算机，解决 “存储” 问题。
   • 核心操作：结合存储结构实现算法，解决 “应用” 问题。
   • 老师强调：现阶段重点掌握操作的思想和思路，后续巩固提升阶段会结合编程语言（如 C 语言）实现具体代码。

（2） 数据结构的定义呼应

数据结构的官方定义：逻辑结构 + 存储结构 + 相应的一组操作。

我们的学习流程完全契合该定义，这是学好数据结构的核心逻辑。

5.1 树的基本概念

5.1.1 树的定义

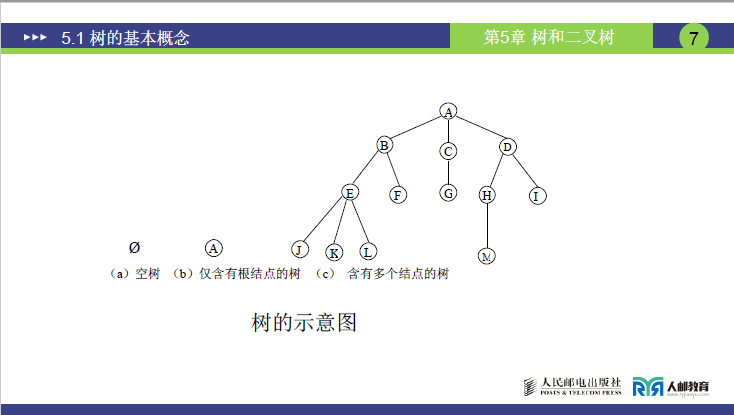
（1）形式化定义

树是由n(n≥0)个结点组成的有限集合（与线性表、栈、队列定义中 “数据元素” 的表述不同，树和后续图结构统一用 “结点” 表述）：

• 若n=0，称为空树；

• 若n>0，需满足两个条件：

  ① 存在一个特定的根结点（root），该结点只有直接后继，无直接前驱；

  ② 除根结点外，其余结点可划分为m(m≥0)个互不相交的有限集合T₀,T₁,...,T_m−1，每个集合T_i都是一棵树（称为根的子树），且子树根结点有且仅有一个直接前驱，可拥有 0 个或多个直接后继。

（2）定义的核心特性

树的定义是递归形式，即子树的定义与整棵树的定义一致，子树可继续划分下一级子树，这是树结构的关键特性，也是后续树相关算法设计的核心逻辑。

（3）树的常见形态

• 空树：无任何结点，是树的特殊形态；
• 仅含根结点的树：只有一个根结点，无任何子树；
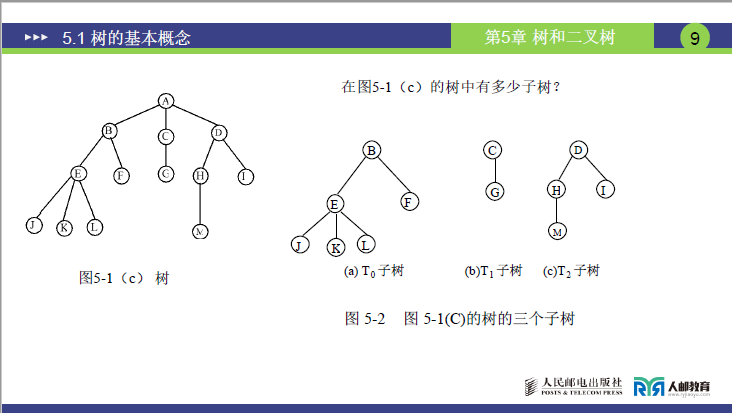
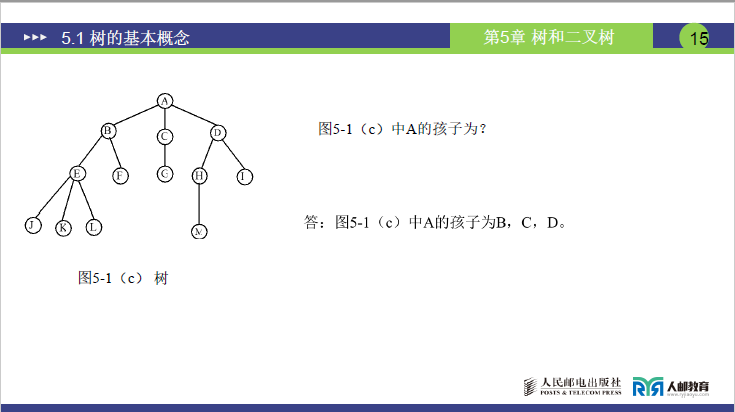
• 含多个结点的树：根结点下挂载若干子树，子树又包含自身的子树，是最常见的树形态（如课件中图 5-1 (c) 的树，根结点 A 下有 3 棵子树）。

（4）子树数量的相对性

子树数量需结合指定的根结点判断：

• 以图中的树为例，若以 A 为根，其子树数量为 3（对应 B、C、D 为根的子树）；
• 若以 B 为根，其子树数量为 2（对应 E、F 为根的子树）。

5.1.2 树的描述

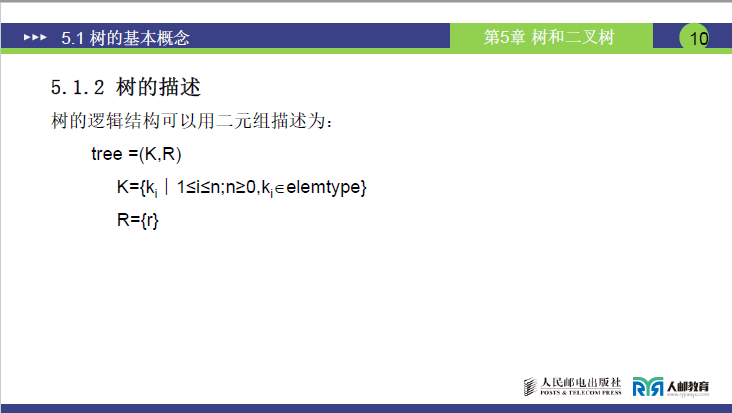
（1）二元组描述法

树的逻辑结构可通过二元组tree=(K,R)精准描述：

• K={k_i∣1≤i≤n;n≥0,k_i∈elemtype}：K是树中所有结点的集合；
• R={r}：r是结点间的关系集合，即结点间的父子关联。

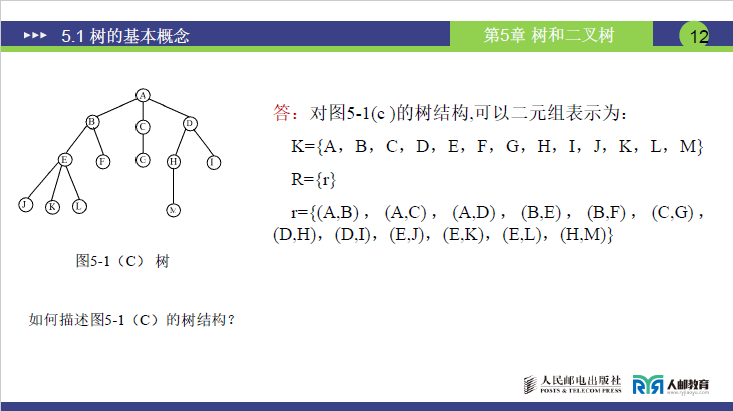
（2）实例应用

以课件中图 5-1 (c) 的树为例，其二元组描述为：

• 结点集合K={A,B,C,D,E,F,G,H,I,J,K,L,M}；
• 关系集合r={(A,B),(A,C),(A,D),(B,E),(B,F),(C,G),(D,H),(D,I),(E,J),(E,K),(E,L),(H,M)}。

（3）双向转换能力

树的图形结构与二元组描述可相互转换：

• 已知树的图形，可提取结点和关系写出二元组；
• 已知二元组，可根据关系集合还原树的图形结构，这是考试中常见的题型。

5.1.3 树的基本术语

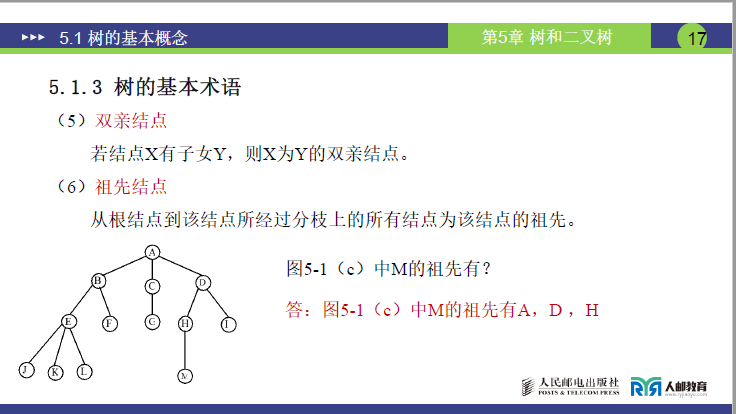
树的术语是后续学习的基础，需精准区分，核心术语如下表所示：

术语	定义	课件实例（图 5-1 (c) 的树）
结点	树中的数据元素，常用字母表示	A、B、C 等均为结点
结点的度	一个结点包含的子树数目	结点 A 的度为 3，结点 B 的度为 2
树叶（叶子）	度为 0 的结点，又称终端结点	J、K、L、F、G、I、M 均为叶子
孩子结点	结点子树的根结点为该结点的孩子（仅指子树根，非子树所有结点）	A 的孩子为 B、C、D；B 的孩子为 E、F
双亲结点	若结点 X 有孩子 Y，则 X 为 Y 的双亲	B 的双亲为 A，E 的双亲为 B
祖先结点	从根结点到该结点路径上的所有结点	M 的祖先为 A、D、H
子孙结点	某结点的孩子及孩子的孩子等所有后代	A 的子孙包含除自身外的所有结点
兄弟结点	具有同一双亲的结点（仅指同胞，不含堂兄 / 表兄）	B、C、D 互为兄弟，E、F 互为兄弟
树的度	树中所有结点度的最大值（具有唯一性）	图 5-1 (c) 树中 E 的度为 3，为最大值，故树的度为 3
树的层数	根结点层数为 1，其余结点层数为根到该结点的分支数 + 1	根 A 层数为 1，B/C/D 层数为 2，E/F/G/H/I 层数为 3
树的高度（深度）	树中结点的最大层数	图 5-1 (c) 树中 J/K/L/M 层数为 4，故树的高度为 4
有序树 / 无序树	子树有固定左右顺序为有序树，反之则为无序树	生活中树多为无序树，子树顺序可互换；二叉树为有序树
森林	若干棵互不相交的树组成的集合，一棵树是特殊森林	若将图 5-1 (c) 树的根 A 移除，其 3 棵子树就构成森林

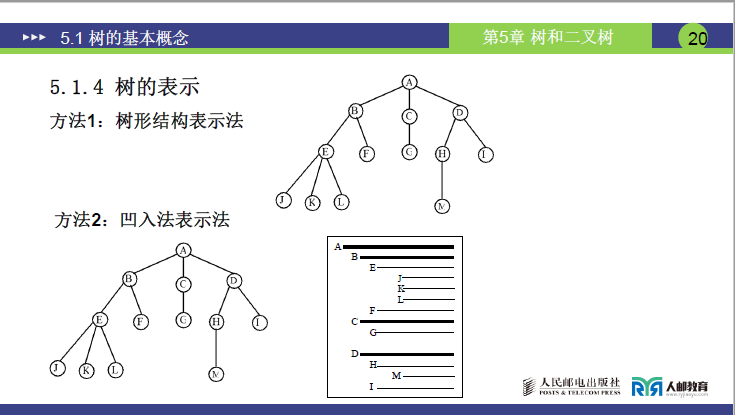
5.1.4 树的表示方法

树有 4 种常用表示方法，适用于不同场景：

1. 树形结构表示法
   • 特点：最直观，用圆圈表示结点，连线表示结点间关系，能清晰体现树的层级和父子关联；
   • 适用场景：日常学习、考试答题的首选表示方法。
2. 凹入法表示法
   • 特点：通过结点的缩进程度体现层级，根结点缩进最少，子结点依次缩进；
   • 不足：对复杂树的表示不够清晰，且对缩进格式要求严格。
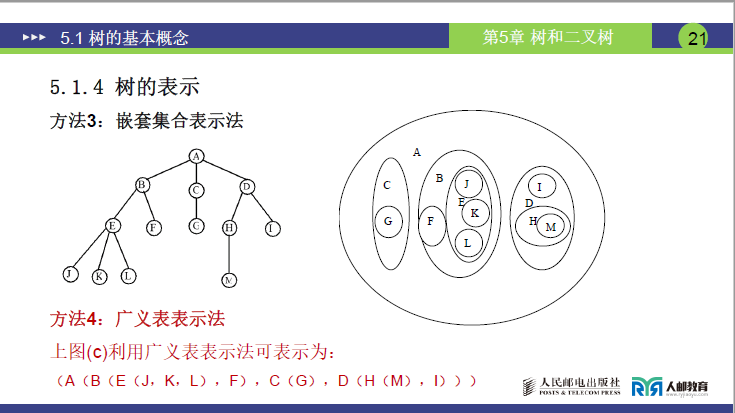
3. 嵌套集合表示法
   • 特点：用集合嵌套的形式展现结点的从属关系，根结点对应最大集合，子结点对应嵌套的子集合；
   • 不足：复杂树的集合嵌套会过于繁琐，不易理解。
4. 广义表表示法
   • 特点：将树的结构转化为广义表格式，根结点写在最前，子树用括号包裹，子树间用逗号分隔；
   • 实例：课件中图 5-1 (c) 的树可表示为(A(B(E(J,K,L),F),C(G),D(H(M),I)))；
   • 适用场景：便于计算机存储和处理，在科研及高级编程中会用到。

5.1.5 树的性质

明确说明，树的性质需结合二叉树的性质进行学习和掌握，核心逻辑如下：

1. 学习逻辑

   树的结构复杂（结点子树数量不固定），直接研究其性质难度较高；而二叉树每个结点度≤2，结构规整，性质易推导，因此先掌握二叉树性质，再通过树与二叉树的转换关系，反推树的性质。

2. 核心关联

   后续会学习 “树转二叉树” 的方法，树的层数、结点数等性质可通过转换后的二叉树性质间接推导，例如树的高度可对应转换后二叉树的深度。

5.2 二叉树的基本概念

5.2.1 二叉树的定义

（1）严谨定义​

二叉树是节点的有限集合，该集合满足以下两个条件之一：

• 集合为空（空二叉树）；

• 由一个根节点和两棵互不相交的、分别称为左子树和右子树的二叉树组成。

（2）核心判断依据

从节点度数角度可简化判断：二叉树中每个节点的度≤2（度指节点的子节点个数，即 “分叉数”）。

根据度数不同，二叉树的节点可分为三类：

• 度为 0 的节点：叶子节点（无子女节点）；

• 度为 1 的节点：仅有一个左子节点或右子节点；

• 度为 2 的节点：同时有左、右两个子节点。

（3）关键特性：有序性

• 普通树为无序树，子树的左右顺序可互换；

• 二叉树为有序树，左、右子树的位置不可颠倒，若交换则视为两棵不同的二叉树。例如根节点的左子树根为 B、右子树根为 C，交换后会形成新的二叉树。

（4）树与二叉树的关系

• 二叉树一定是树；

• 树不一定是二叉树（若树中存在度＞2 的节点，则无法称为二叉树）。

5.2.2 二叉树的形态

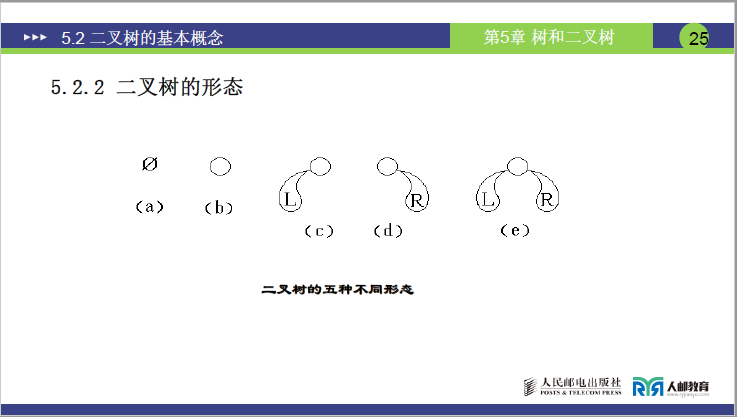
二叉树共有五种基本形态，涵盖了所有可能的结构：

• 空二叉树：无任何节点；
• 仅有根节点：只有一个度为 0 的根节点，无左右子树；
• 仅有左子树：根节点只有左子树，无右子树；
• 仅有右子树：根节点只有右子树，无左子树；
• 同时有左、右子树：根节点既有左子树，也有右子树（完整的基础二叉树结构）。

注：形态 3 和形态 4 为不同二叉树，核心原因是二叉树的有序性。

5.2.3 二叉树的性质

二叉树共有 5 个核心性质，是后续解题和深入学习的关键，其中性质 1-3 为基础必备知识点。

性质 1：某一层的最大节点数

若二叉树的层数从 1 开始计数，则第i层上最多有2ⁱ−1个节点。

• 示例验证：

  • 第 1 层（根节点层）：2⁰=1个节点；

  • 第 2 层：2¹=2个节点；

  • 第 3 层：2²=4个节点，以此类推。

性质 2：深度为 k 的二叉树的最大节点总数

二叉树的深度（又称高度）指树中最大的层数，若深度为k，则该二叉树最多有2^k−1个节点。

• 公式推导：

  深度为k的二叉树，节点总数为各层最大节点数之和，即等比数列求和：2⁰+2¹+2²+...+2^k−1=2^k−1；

• 示例验证：

  深度为 3 的二叉树，最多节点数为2³−1=7个，即每层都达到最大节点数的满结构。

性质 3：叶子节点与度为 2 的节点数量关系

对任意一棵非空二叉树，若其叶子节点数为n0，度为 2 的节点数为n2，则恒有 n₀=n₂+1（叶子节点数比度为 2 的节点数多 1）。

• 严谨证明：

1. 设二叉树总节点数为n，度为 1 的节点数为n₁，则总节点数满足n=n₀+n₁+n₂；
2. 从 “子节点总数” 角度分析：度为 0 的节点无子女，度为 1 的节点有 1 个子女，度为 2 的节点有 2 个子女，因此子节点总数为0×n₀+1×n₁+2×n₂=n₁+2n₂；
3. 二叉树中除根节点外，其余节点均为某一节点的子节点，因此总节点数n=子节点总数+1=n₁+2n₂+1；
4. 联立两个总节点数公式：n₀+n₁+n₂=n₁+2n₂+1，消去n1后可得n₀=n₂+1。

性质 4：n 个节点的完全二叉树的深度

具有n个节点的完全二叉树，其深度k=⌊log₂n⌋+1（⌊log₂n⌋表示对log₂n向下取整）。

• 推导逻辑：

1. 设完全二叉树深度为k，则深度为k−1的满二叉树最多有2^k−1−1个节点，深度为k的满二叉树最多有2^k−1个节点；
2. 完全二叉树节点数n满足2^k−1−1＜n ≤2^k−1，变形得2^k−1≤ n ≤2^k；
3. 对不等式取对数得k−1≤log₂n<k，因k为整数，故k=⌊log₂n⌋+1。

性质 5：完全二叉树的节点编号规则

对完全二叉树的节点按层序遍历顺序（从上到下、从左到右）从 1 开始编号，节点编号满足以下规律：

1.若节点编号为i（i>1），则其双亲节点编号为⌊i/2⌋；

• 示例：编号 2 的节点双亲为⌊2/2⌋=1，编号 3 的节点双亲为⌊3/2⌋=1；

2.若节点编号为i，则其左孩子节点编号为2i（若2i≤n，n为总节点数，否则无左孩子）；

3.若节点编号为i，则其右孩子节点编号为2i+1（若2i+1≤n，否则无右孩子）。

5.2.4 两类特殊二叉树

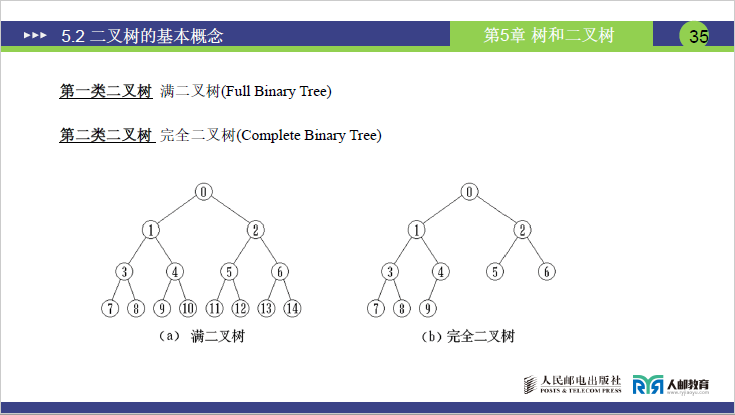
（1）满二叉树

①定义

满二叉树需同时满足两个条件：

• 树中仅存在度为 0 和度为 2 的节点（无度为 1 的节点）；

• 所有叶子节点都在最底层（叶子节点的层数等于树的深度）。

②核心特性

• 若满二叉树深度为k，则总节点数为2^k−1，且叶子节点数为2^k−1；

• 满二叉树是结构最 “紧凑” 的二叉树，每层节点数均达到最大值。

（2）完全二叉树

①简易判断方法

按层序遍历顺序对节点从 1 开始编号，若所有节点的编号与相同深度的满二叉树节点编号完全连续，则为完全二叉树。

②核心特性

• 叶子节点仅可能出现在最下面两层，且最下层叶子节点均靠左排列；

• 度为 1 的节点若存在，最多有 1 个，且该节点只有左孩子、无右孩子；

• 满二叉树一定是完全二叉树，但完全二叉树不一定是满二叉树（完全二叉树允许最底层节点未填满，且需满足左密右疏）。

5.3 二叉树的存储结构

5.3.1存储结构的整体分类

二叉树作为数据结构的重要类型，其存储结构从广义上可分为顺序存储、链式存储、索引存储、散列存储四类，其中顺序存储和链式存储是二叉树存储的核心与重点，需重点掌握。

5.3.2顺序存储结构（数组表示）

（1）核心原理

二叉树的顺序存储依托二叉树的性质 5实现，即对有 n 个结点的完全二叉树按层序（自顶向下、同层自左向右）编号 1~n 后，结点 i（1≤i≤n）满足以下关系：

• 若 i=1，为根结点，无双亲；若 i>1，双亲为⌊i/2⌋
• 若 2i≤n，左孩子为 2i；否则无左孩子
• 若 2i+1≤n，右孩子为 2i+1；否则无右孩子
• 偶数 i（i≠n）的右兄弟为 i+1，奇数 i（i≠1）的左兄弟为 i-1

顺序存储本质是将二叉树结点按上述编号顺序存入一维数组，数组下标与结点编号一一对应，以此实现二叉树的存储与结构还原。

（2）存储步骤

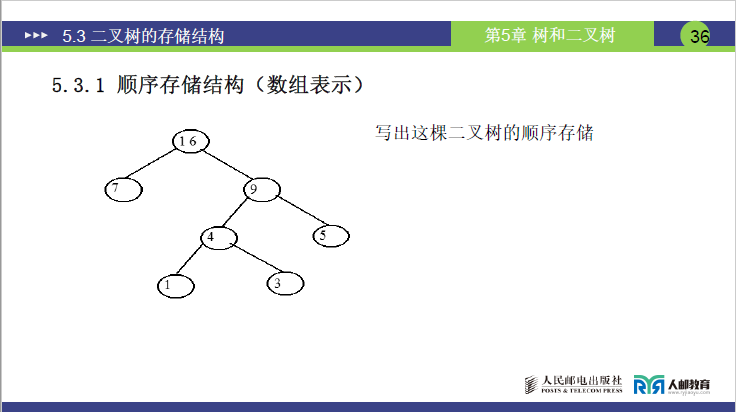
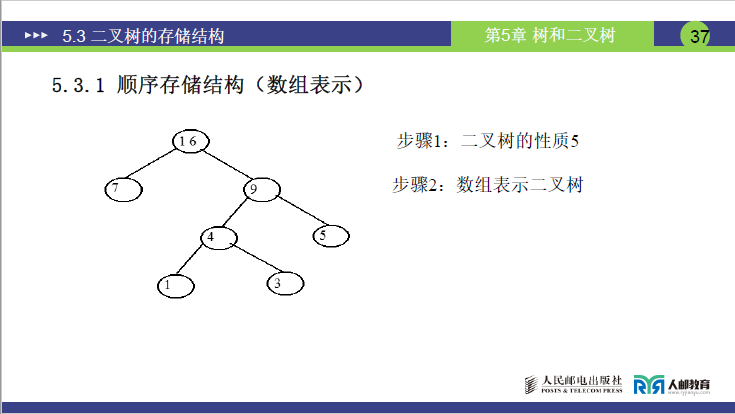
1. 编号：依据二叉树性质 5，对二叉树所有结点完成层序编号，明确每个结点的编号位置
2. 数组存储：申请对应长度的数组，将结点按编号依次存入数组对应下标位置（通常 0 号下标闲置，从 1 号开始存储以匹配编号）

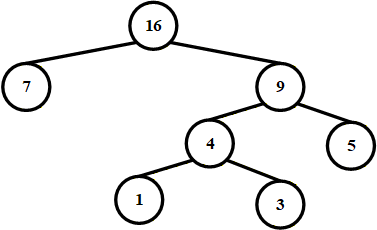
写出这棵二叉树的顺序存储

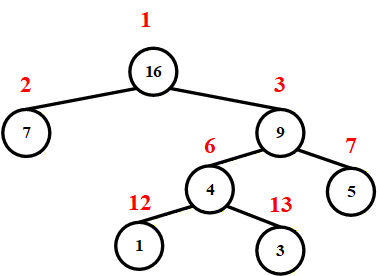
序号	1	2	3	4	5	6	7	8	9	10	11	12	13
值	16	7	9			4	5					1	3

（3）不同二叉树的存储特点

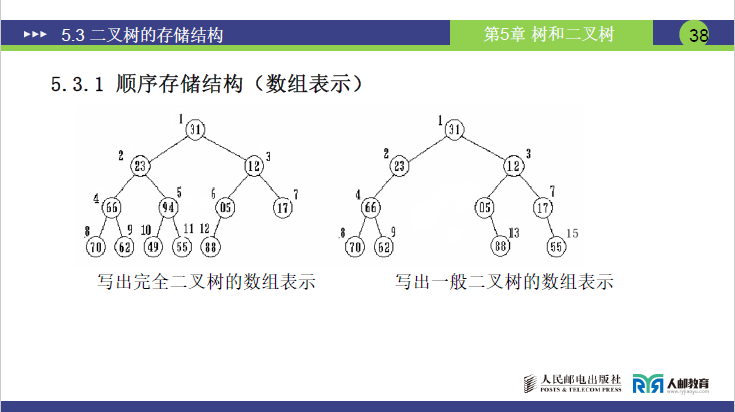
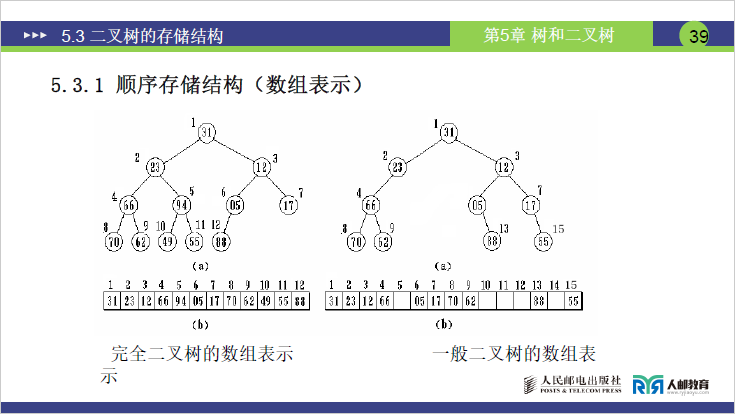
• 完全二叉树 / 满二叉树：编号连续，数组无闲置空间，空间利用率 100%，是顺序存储的最优适配场景
• 普通二叉树：需按完全二叉树的规则补全编号，会出现数组 “空位置”，存在一定空间浪费
• 单分支二叉树（尤其是右单分支）：空间浪费极端。如深度为 5 的右单分支二叉树，需申请长度为 31 的数组（满二叉树结点数 2^5-1=31），但仅 5 个位置存有效结点，其余均为闲置

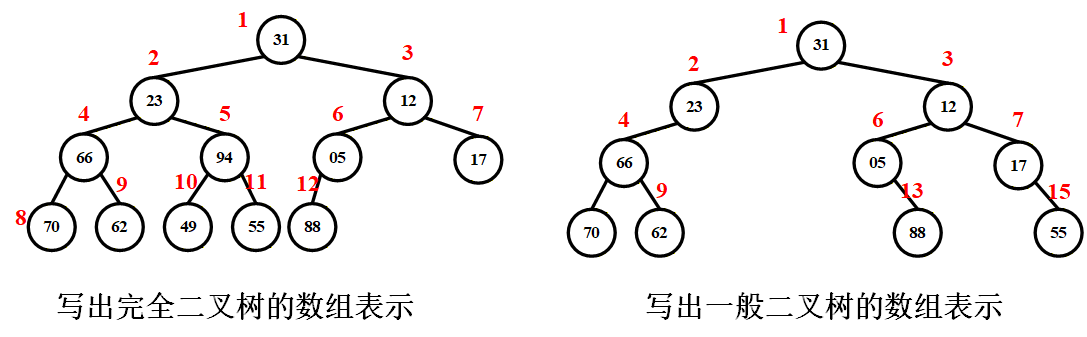
序号	1	2	3	4	5	6	7	8	9	10	11	12
值	31	23	12	66	94	05	17	70	62	49	55	88

序号	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
值	31	23	12	66		05	17	70	62				88		55

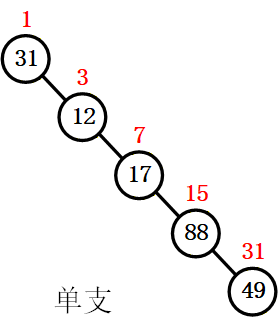
序号	1	...	3	...	7	...	15	...	31
值	31	...	12	...	17	...	88	...	49

（4）关键结论

顺序存储的优势是实现简单、可直接通过下标定位结点双亲与孩子；劣势是对非完全 / 满二叉树空间利用率低，仅适用于形态规整的二叉树。

5.3.3链式存储结构（指针表示）

（1）存储结构分类

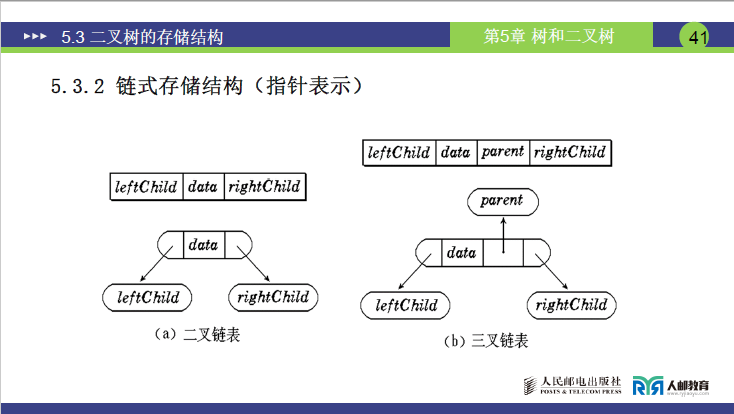
二叉树的链式存储基于链表实现，核心有二叉链表和三叉链表两种结构，其中二叉链表为常用结构。

存储结构	结点组成	适用场景
二叉链表	1 个数据域+2 个指针域（leftChild 指向左孩子、rightChild 指向右孩子）	常规二叉树存储，兼顾空间与功能
三叉链表	1 个数据域+3 个指针域（leftChild、rightChild+parent 指向双亲）	需频繁查找双亲结点的场景，空间开销略高

（2）二叉链表存储实例

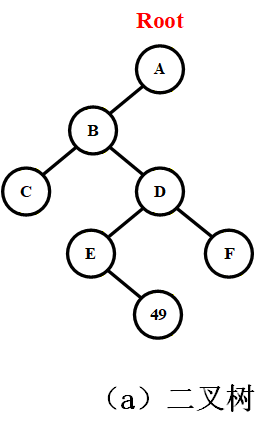
写出二叉树链表表示：二叉链表

设二叉树结点为 A（根）、B（A 左孩子）、C（B 左孩子）、D（B 右孩子）、E（D 左孩子）、F（D 右孩子）、G（E 右孩子），其二叉链表存储逻辑如下：

• 根结点 A：leftChild→B，rightChild→NULL
• 结点 B：leftChild→C，rightChild→D
• 结点 C：leftChild→NULL，rightChild→NULL（叶子结点）
• 结点 D：leftChild→E，rightChild→F
• 结点 E：leftChild→NULL，rightChild→G
• 结点 F：leftChild→NULL，rightChild→NULL（叶子结点）
• 结点 G：leftChild→NULL，rightChild→NULL（叶子结点）

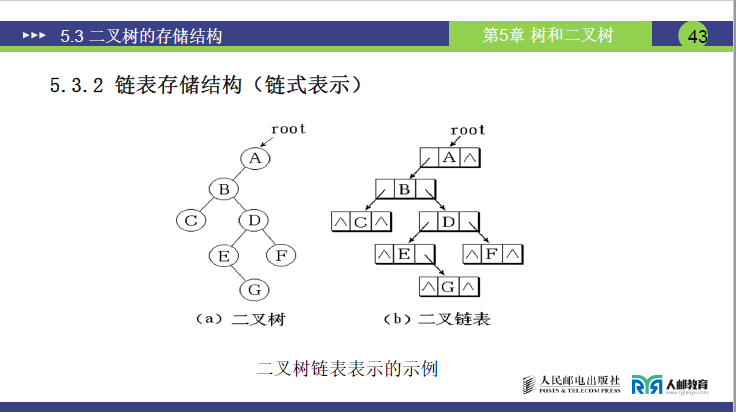
（3）核心特点

• 空间利用率：仅需 n 个结点空间（n 为二叉树结点数），无闲置空间，适配任意形态二叉树
• 结构灵活性：可便捷实现二叉树的插入、删除操作，且能直观体现结点间的父子关系
• 叶子结点判定：二叉链表中，leftChild 和 rightChild 均为 NULL的结点为叶子结点

5.3.4两种存储结构的对比

对比维度	顺序存储	链式存储
存储载体	一维数组	二叉链表 / 三叉链表
空间效率	完全 / 满二叉树高，普通 / 单分支二叉树低	所有形态二叉树均为高效，无空间浪费
操作便捷性	查找双亲 / 孩子快（下标计算），插入删除难	插入删除灵活，查找双亲需遍历（二叉链表）
适配场景	完全 / 满二叉树的静态存储	任意形态二叉树的动态操作（增删改查）

5.4二叉树的遍历---操作1

5.4.1遍历的本质​

二叉树的遍历指按某一次序访问树中所有节点，且每个节点仅被访问一次的过程，最终会将非线性结构的二叉树转化为节点的线性序列，为后续数据处理提供基础。

5.4.2遍历的分类逻辑​

以根节点（记为D）、左子树（记为L）、右子树（记为R）的访问顺序为核心，可推导多种遍历方式：

• 基础排列（先左后右）：共 3 种，分别为先序（根→L→R）、中序（L→根→R）、后序（L→R→根）；

• 逆序排列（先右后左）：共 3 种，对应为逆先序（根→R→L）、逆中序（R→根→L）、逆后序（R→L→根），仅需了解概念，无需深入掌握；

• 特殊遍历：按层次遍历（自上到下、自左到右）；

• 考试重点：先序、中序、后序（先左后右系列）+ 按层次遍历，共 4 类。

5.4.2先序遍历（Preorder Traversal，又称前序遍历）

（1）递归遍历规则

• 若二叉树为空，则不执行任何操作；

• 若二叉树非空，执行顺序为：访问根节点 → 先序遍历左子树 → 先序遍历右子树（即D→L→R）。

• 核心特点：遍历算法为递归定义，与树的递归本质（树的子树仍是树）相契合。

（2）求下面二叉树遍历结果（前缀表达式）

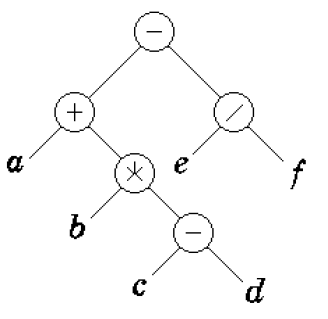
先序遍历的执行步骤为：

• 访问根节点（最外层减号）；
• 先序遍历左子树（根为加号，依次访问加号→a→乘号→b→减号→c→d）；
• 先序遍历右子树（根为除号，依次访问除号→E→F）；

最终遍历序列：- + a * b - c d / e f。

（3）关联拓展：

先序遍历序列对应前缀表达式（运算符在操作数前方），也叫波兰式。

5.4.2 中序遍历（Inorder Traversal）

（1）递归遍历规则

• 若二叉树为空，不执行操作；

• 若二叉树非空，执行顺序为：中序遍历左子树 → 访问根节点 → 中序遍历右子树（即L→根→R）。

• 核心特点：根节点的访问位于左右子树遍历的中间。

（2）实例演示（同表达式二叉树）

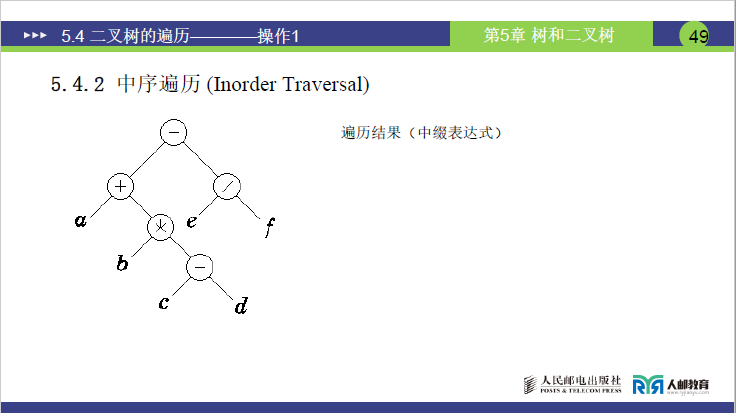
执行步骤为：

1. 中序遍历左子树（A→加号→B→乘号→C→减号→D）；
2. 访问根节点（外层减号）；
3. 中序遍历右子树（E→除号→F）；

最终遍历序列：A + B * C - D - E / F。

（3）关联拓展：

中序遍历序列对应中缀表达式（运算符在操作数中间），是日常使用的表达式形式。但中缀表达式计算需借助两个栈（数据栈 + 运算符栈）处理优先级和括号问题，效率较低。

5.4.3 后序遍历（Postorder Traversal）

（1）递归遍历规则

• 若二叉树为空，不执行操作；

• 若二叉树非空，执行顺序为：后序遍历左子树 → 后序遍历右子树 → 访问根节点（即L→R→根）。

• 核心特点：根节点的访问位于左右子树遍历之后，运算符会出现在操作数后方。

（2）实例演示（同表达式二叉树）

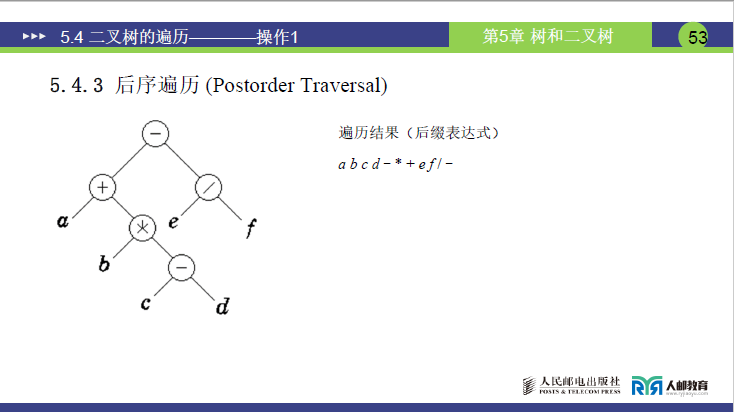
执行步骤为：

1. 后序遍历左子树（A→B→C→D→减号→乘号→加号）；
2. 后序遍历右子树（E→F→除号）；
3. 访问根节点（外层减号）；

最终遍历序列：A B C D - * + E F / -。

（3）关联拓展：

后序遍历序列对应后缀表达式（运算符在操作数后方），又称逆波兰式。该表达式计算仅需一个栈即可完成，无需处理优先级和括号，是编译原理中表达式计算的常用形式。

5.4.4例题分析（对应课件 5.4.4）

课堂例题分为基础遍历求解和进阶二叉树构造两类，是考试高频考点：

类型 1：已知二叉树，求三种遍历序列

例题 1（基础二叉树）

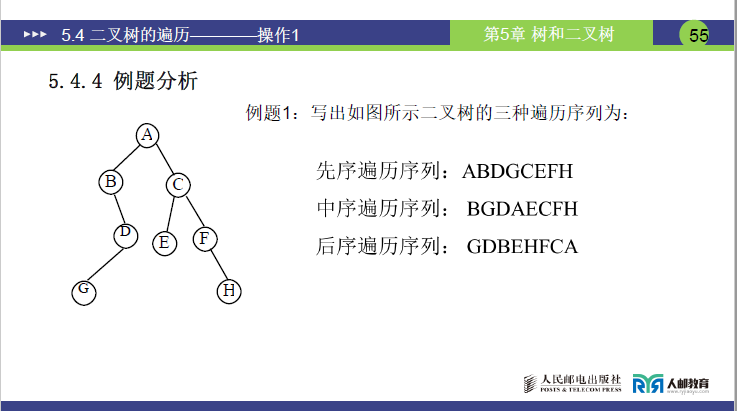
给定二叉树根为 A，左子树根为 B（B 无左子树，右子树为 D（D 右子树为 G）），右子树根为 C（C 左子树为 E，右子树为 F（F 右子树为 H）），求解三种遍历序列：

• 先序遍历（根→L→R）：A B D G C E F H

• 中序遍历（L→根→R）：B G D A E C F H

• 后序遍历（L→R→根）：G D B E H F C A

例题 2（简单表达式二叉树）

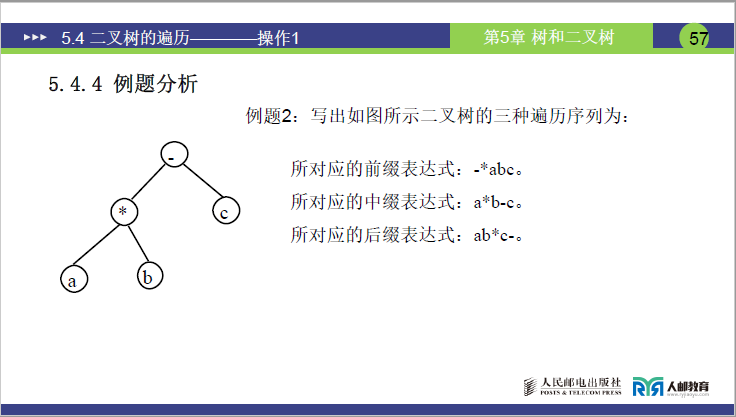
表达式对应的二叉树，根为减号，左子树为 A 和 B 的乘号子树，右子树为 C，求解序列：

• 先序（前缀表达式）：- * A B C

• 中序（中缀表达式）：A * B - C

• 后序（后缀 / 逆波兰式）：A B * C -

类型 2：已知遍历序列，构造唯一二叉树

核心结论

• 可唯一确定的组合：先序 + 中序、后序 + 中序（均需中序序列确定左右子树范围）；

• 不可唯一确定的组合：先序 + 后序（仅能确定根节点，无法区分左右子树）。

实例（先序 + 中序构造二叉树）

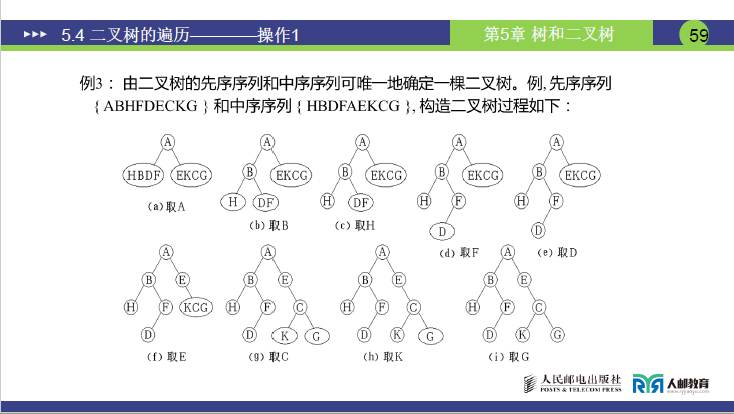
已知先序序列：A B H F D E K C G，中序序列：H B D F A E K C G，构造步骤如下：

1. 确定根节点：先序序列首元素为根，即根为 A；
2. 划分左右子树：在中序序列中，A 左侧H B D F为左子树，右侧E K C G为右子树；
3. 递归确定子树根
   • 左子树：先序中 A 的下一个元素为 B，即左子树根为 B；在中序中 B 左侧为 H（B 的左子树），右侧D F为 B 的右子树；继续递归，先序中 B 的下一个为 F（右子树根），中序中 F 左侧为 D（F 的左子树）；
   • 右子树：先序中左子树元素后为 E，即右子树根为 E；中序中 E 左侧无元素（E 无左子树），右侧K C G为 E 的右子树；继续递归，先序中 E 的下一个为 C（右子树根），中序中 C 左侧为 K（C 的左子树），右侧为 G（C 的右子树）；
4. 得到二叉树：按上述步骤可唯一还原二叉树，进而可推导后序序列为H D F B K G C E A。

5.4.5知识延伸与后续衔接

（1）二叉链表的指针浪费问题​

对于含N个节点的二叉链表，共定义2N个指针域：

• 已使用指针数：除根节点外，每个节点均有一个父指针指向它，故使用N-1个；
• 未使用指针数：2N - (N-1) = N+1个，存在大量空间浪费。

（2）后续内容衔接

为充分利用空指针域，可将其改造为指向节点的前序 / 中序 / 后序前驱或后继，实现遍历过程的简化，这便是下一节要学习的二叉树的线索化（线索二叉树）。

5.4.6课堂重点小结

1. 二叉树遍历的核心是根、左子树、右子树的访问次序，考试重点为前序、中序、后序（先左后右）和层次遍历；
2. 三种基础遍历对应三种表达式：前序→前缀、中序→中缀、后序→后缀（逆波兰式）；
3. 唯一构造二叉树的组合为先序 + 中序、后序 + 中序，先序 + 后序无法唯一确定；
4. 二叉链表存在N+1个空指针，为线索二叉树的引入提供了必要性。

5.5 线索二叉树 / 二叉树的线索化

5.5.1 线索二叉树（Threaded Binary Tree）的基本概念

（1）引入背景

在二叉树的二叉链表存储结构中，若二叉树有n个结点，则会分配2n个指针域。而二叉树中除根结点外，每个结点都有且仅有一个双亲，因此实际用于指向孩子的有效指针仅n−1个，剩余n+1个指针域为空，造成了存储空间的浪费。为了充分利用这些空指针域，引入了线索二叉树。

（2）核心定义

• 线索：将二叉链表中空指针域重新利用，使其指向结点在某一遍历序列中的直接前驱或直接后继，这类特殊的指针称为线索。
• 线索化：将二叉树中空指针域改造为线索的过程，称为二叉树的线索化。
• 线索二叉树：完成线索化改造后的二叉树，其对应的存储结构为线索二叉链表。
• 核心实质：对二叉树这一非线性结构进行线性化处理，使得除序列首末结点外，其余每个结点都有且仅有一个直接前驱和一个直接后继。

（3）关键前提

结点的直接前驱和直接后继的判定依赖于二叉树的遍历顺序，不同遍历顺序下，同一结点的前驱和后继可能完全不同，因此线索化操作必须结合具体的遍历方式进行。

5.5.2 线索二叉树的类型

根据线索化时所依据的二叉树遍历顺序，线索二叉树分为三类，其分类核心是 “前驱 / 后继的判定标准由遍历顺序决定”：

1. 前序线索二叉树
   • 按前序遍历（根→左→右）的序列为结点添加前驱、后继线索，线索指针指向的是前序序列中的直接前驱和直接后继。
2. 中序线索二叉树
   • 按中序遍历（左→根→右）的序列为结点添加线索，是最常用的线索二叉树类型。
3. 后序线索二叉树
   • 按后序遍历（左→右→根）的序列为结点添加线索，其线索指向的是后序序列中的前驱和后继。

5.5.3 线索二叉树的链式存储结构

（1）结点结构设计

为区分指针域是指向孩子还是指向线索，在原二叉链表结点的基础上增加两个标志域（ltag和rtag），最终结点包含 5 个域，结构如下：

域名称	取值与含义
ltag	0：lchild指向该结点的左孩子；1：lchild指向该结点的直接前驱（线索）
lchild	左孩子指针或前驱线索指针
data	结点的数据域
rchild	右孩子指针或后继线索指针
rtag	0：rchild指向该结点的右孩子；1：rchild指向该结点的直接后继（线索）

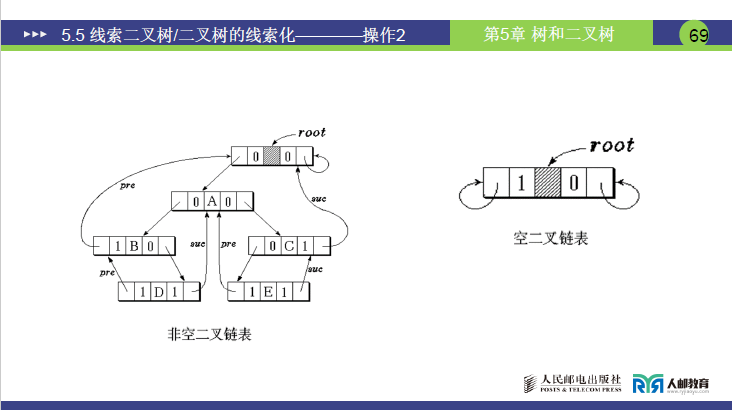
（2）带头结点的线索二叉链表

为方便遍历操作的实现，可给线索二叉树添加头结点，其指向规则如下：

• 头结点的lchild：若二叉树非空，指向二叉树的根结点；若为空，指向自身。
• 头结点的ltag：非空树时为 0（指向根，视为左孩子），空树时为 1（指向自身，视为线索）。
• 头结点的rchild：始终指向自身。
• 头结点的rtag：始终为 0（指向自身，视为右孩子）。
• 遍历序列的首结点的lchild（ltag=1时）和尾结点的rchild（rtag=1时）均指向头结点，形成闭环，便于首尾结点的前驱 / 后继查找。

5.5.4 线索二叉树举例

（1）中序线索二叉树

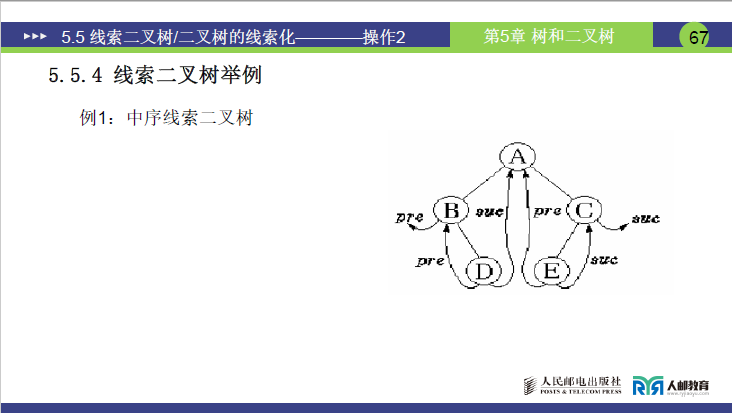
①遍历基础

以二叉树（结点为 A、B、D、E、C）为例，其中序遍历序列为B→D→A→E→C。

②线索化过程

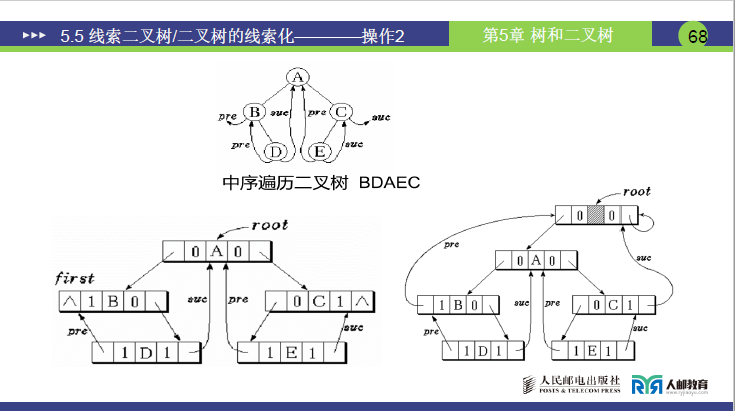
• 根结点 A：左右孩子均存在，ltag=0、rtag=0，lchild指向 B、rchild指向 C。
• 结点 B：仅右孩子（D）存在，左指针为空，ltag=1（指向前驱）、rtag=0；因 B 是中序序列首结点，其lchild（线索）指向头结点。
• 结点 D：无左右孩子（叶子结点），ltag=1、rtag=1；lchild指向前驱 B，rchild指向后继 A。
• 结点 E：无左右孩子，ltag=1、rtag=1；lchild指向前驱 A，rchild指向后继 C。
• 结点 C：仅左孩子（E）存在，右指针为空，ltag=0、rtag=1；因 C 是中序序列尾结点，其rchild（线索）指向头结点。

（2）前序线索二叉树

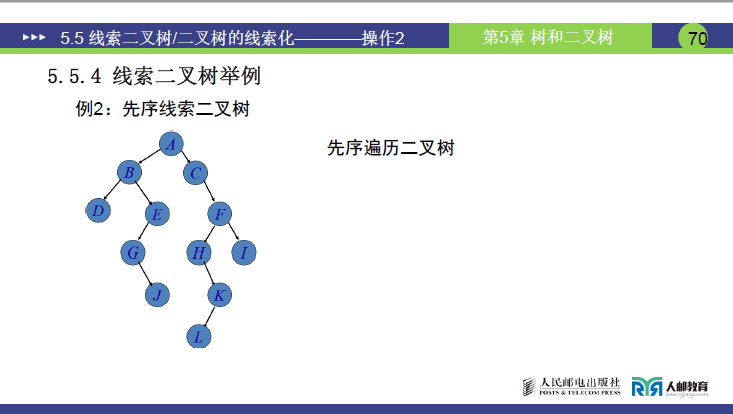
①遍历基础

以含结点 A、B、D、E、G、J、C、F、H、K、L、I 的二叉树为例，其前序遍历序列为ABDEGJCFHKLI。

②线索化过程

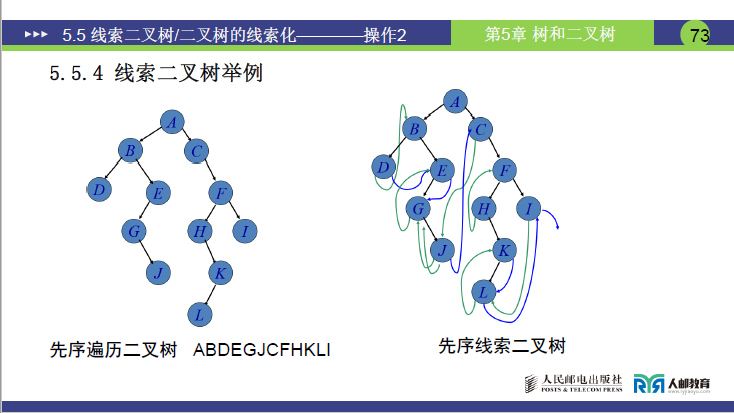
• 核心规则：按前序 “根→左→右” 判定前驱和后继，空指针域转为线索。
• 典型结点处理：
  • 结点 D（叶子）：无左右孩子，ltag=1、rtag=1；前驱为 B，lchild指向 B；后继为 E，rchild指向 E。
  • 结点 C：无左孩子、有右孩子，ltag=1、rtag=0；前驱为 J，lchild指向 J；rchild指向 F。
  • 结点 L（叶子）：无左右孩子，ltag=1、rtag=1；前驱为 K，lchild指向 K；后继为 I，rchild指向 I。

（3）后序线索二叉树

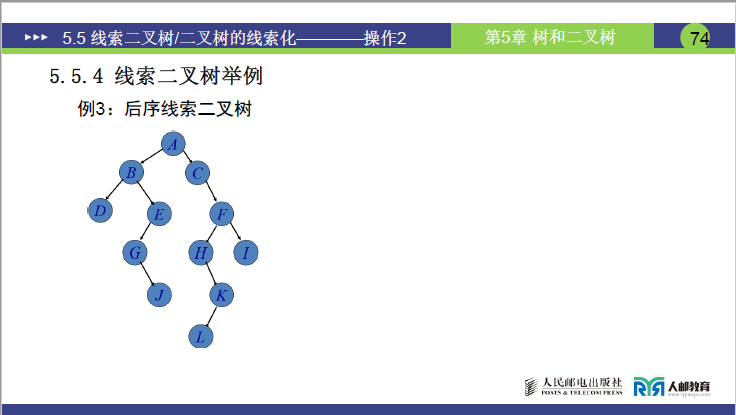
①遍历基础

同上述复杂二叉树，其后序遍历序列为DJGEBLKHIFCA。

②线索化过程

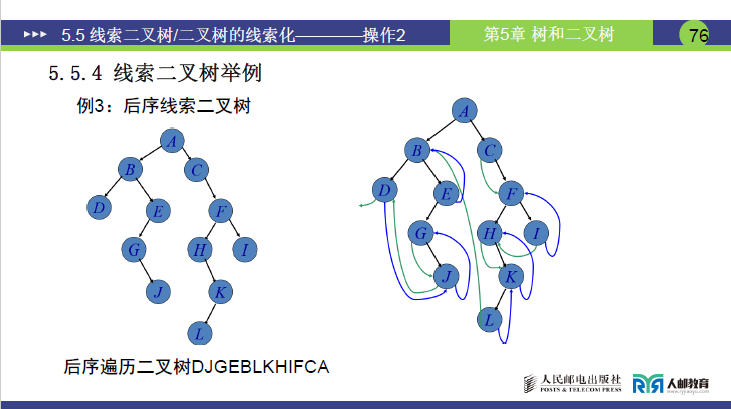
• 核心规则：按后序 “左→右→根” 判定前驱和后继，空指针域转为线索。
• 典型结点处理：
  • 结点 D（叶子）：无左右孩子，ltag=1、rtag=1；因 D 是后序序列首结点，前驱为空；后继为 J，rchild指向 J。
  • 结点 L（叶子）：无左右孩子，ltag=1、rtag=1；前驱为 B，lchild指向 B；后继为 K，rchild指向 K。
  • 结点 I：无左右孩子，ltag=1、rtag=1；前驱为 H，lchild指向 H；后继为 F，rchild指向 F。

补充扩展与易错点

（1）标志域的核心作用

计算机无法区分指针域是指向孩子还是线索，因此ltag和rtag是关键区分依据，不可省略；若省略标志域，会导致指针功能混淆，无法正确遍历。

（2）线索化与遍历的关联

线索二叉树的构造必须基于某一确定的遍历顺序，同一棵二叉树不同遍历顺序下的线索二叉树结构完全不同，且线索仅对当前遍历序列有效。

（3）带头结点的优势

带头结点的线索二叉树可统一处理序列首末结点的前驱 / 后继（均指向头结点），避免了首结点无前驱、尾结点无后继的特殊情况，简化了遍历算法的逻辑。

5.6 哈夫曼树及其应用

5.6.1 基本概述

（1）核心概念

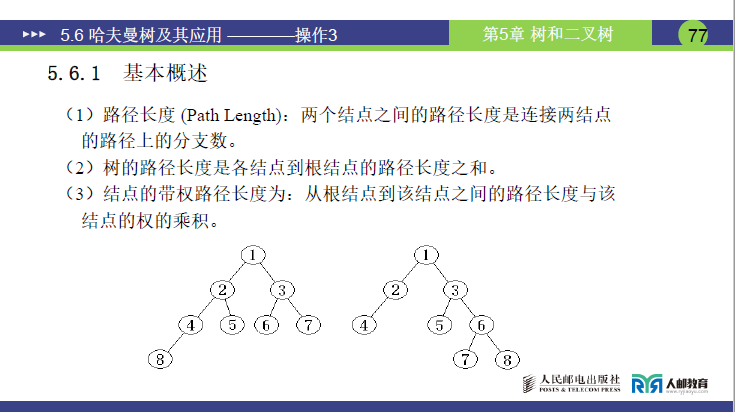
数据结构中 “路径”“带权路径长度” 等术语是描述树结构、设计算法的规范用语，需准确掌握，后续查找、排序等章节也会用到类似逻辑。

1. 路径长度
   • 课件定义：两个结点之间的路径长度是连接两结点的路径上的分支数。
   • 老师补充：路径长度仅统计 “分支数量”，与结点权值无关，是描述结点间距离的基础指标。例如，根结点到其直接子结点的路径长度为 1，根结点到孙结点的路径长度为 2。
2. 树的路径长度
   • 课件定义：各结点到根结点的路径长度之和。
   • 老师解释：树的路径长度是 “所有结点到根的距离总和”，一棵确定的树其路径长度唯一。例如，仅含根结点的树，路径长度为 0；根 + 2 个直接子结点的树，路径长度为 1+1=2。
3. 结点的带权路径长度
   • 课件定义：从根结点到该结点之间的路径长度与该结点的权的乘积。
   • 老师强调：“权” 可理解为结点的 “重要性” 或 “出现频率”（如报文编码中字符的出现次数），该指标体现单个结点的 “加权距离”—— 权值越大的结点，若路径长度过长，会显著增加总代价。
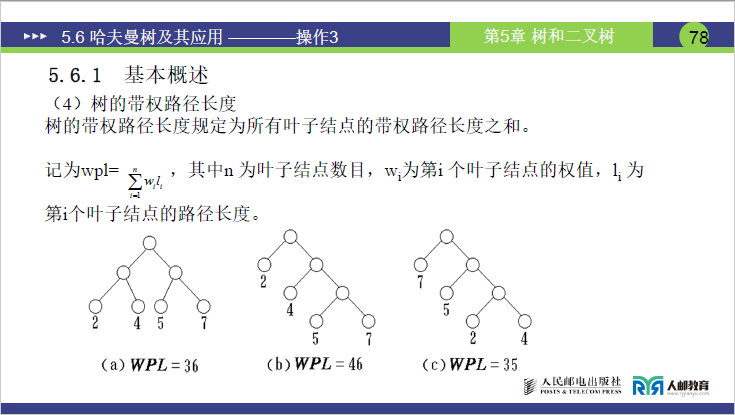
4. 树的带权路径长度（WPL）
   • 课件定义：所有叶子结点的带权路径长度之和，公式为 \(WPL = \sum_{i=1}^{n} w_i l_i\)（其中 n 为叶子结点数目，w_i 为第i个叶子结点的权值，l_i 为第i个叶子结点到根的路径长度）。
   • 老师补充：WPL 是衡量树 “最优性” 的核心指标，仅统计叶子结点（非叶子结点为合并生成，无实际业务意义，如编码中的 “字符” 仅对应叶子）；计算时需先确定每个叶子的路径长度，再与权值相乘后求和。

（2）实例：计算三棵树的 WPL（对应课件 78 页图：三棵二叉树，分别标注 WPL=36、WPL=46、WPL=35）

课件中三棵树的叶子结点权值均为2、4、5、7，但结构不同，导致 WPL 不同，老师详细推导了每棵树的计算过程：

1. 第一棵树（WPL=36）
   • 结构特点：所有叶子结点到根的路径长度均为 2（树为 “平衡结构”，叶子集中在同一层）。
   • 计算过程：WPL=2×2+4×2+5×2+7×2=(2+4+5+7)×2=18×2=36。
2. 第二棵树（WPL=46）
   • 结构特点：叶子结点路径长度不同（权 2 的路径长度为 1，权 4 为 2，权 5、7 为 3）。
   • 计算过程：WPL=2×1+4×2+5×3+7×3=2+8+15+21=46。
3. 第三棵树（WPL=35）
   • 结构特点：权值大的叶子（7）路径长度短（1），权值小的叶子（2、4）路径长度长（3）。
   • 计算过程：WPL=2×3+4×3+5×2+7×1=6+12+10+7=35。

总结：同一组叶子权值，不同树结构的 WPL 差异显著，我们需要找到 WPL 最小的树 —— 即哈夫曼树。

5.6.2 哈夫曼树

（1）课件定义

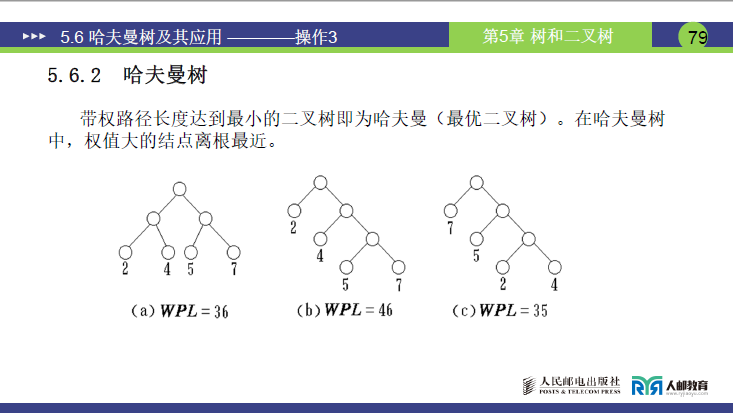
带权路径长度（WPL）达到最小的二叉树，称为哈夫曼树（又称 “最优二叉树”）。

（2）核心特点（老师补充推导）

哈夫曼树的关键特性：权值越大的结点，离根结点越近。

• 原因：结点的带权路径长度是 “权值 × 路径长度”，权值大的结点若离根近（路径长度小），可显著降低其 “加权距离”，进而使总 WPL 最小。
• 实例验证：课件 79 页第三棵树（WPL=35）中，权值最大的叶子（7）路径长度为 1（离根最近），权值最小的叶子（2、4）路径长度为 3（离根最远），符合该特性，因此是哈夫曼树。

5.6.3 哈夫曼树构造

哈夫曼树的构造是 “从叶子到根” 的合并过程，课件给出四步规则，老师结合实例（权值 1、5、7、3）详细拆解了每一步操作（需结合课件 81 页图：哈夫曼树构造过程，含初始森林、一次合并、二次合并、三次合并的四幅子图）。

（1）构造规则

1. 初始状态：将n个权值w1,w2,...,w**n看成n棵树的森林（每棵树仅含一个叶子结点）；
2. 合并操作：在森林中选出根结点权值最小的两棵树，将它们分别作为新树的左、右子树（老师强调：约定 “左子树权值≤右子树权值”，保证构造唯一），新树的根结点权值为两子树根权值之和；
3. 更新森林：从森林中删除刚才选中的两棵树，将新树加入森林；
4. 重复步骤 2-3：直到森林中只剩一棵树，该树即为哈夫曼树。

（2）实例：构造权值为 1、5、7、3 的哈夫曼树

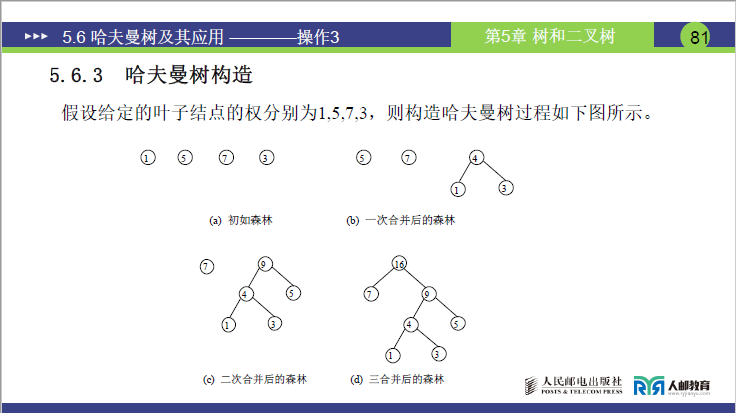
步骤 1：初始森林

• 森林包含 4 棵单结点树，根权值分别为：1、3、5、7（建议先排序，便于选最小的两棵）。

步骤 2：一次合并

• 选权值最小的两棵树：1（左）、3（右）；
• 新树根权值：1+3=4；
• 更新森林：删除 1、3，加入 4，此时森林为：4、5、7。

步骤 3：二次合并

• 选权值最小的两棵树：4（左）、5（右）；
• 新树根权值：4+5=9；
• 更新森林：删除 4、5，加入 9，此时森林为：7、9。

步骤 4：三次合并

• 选权值最小的两棵树：7（左）、9（右）；
• 新树根权值：7+9=16；
• 更新森林：删除 7、9，加入 16，森林仅剩一棵树，即为哈夫曼树。

老师提示：哈夫曼树的叶子结点数 = 初始权值个数（本例中 4 个权值对应 4 个叶子），且哈夫曼树中无度为 1 的结点（仅含度 0 的叶子和度 2 的非叶子），该特性可用于选择题解题（如后续习题 “199 个结点的哈夫曼树有多少叶子”）。

5.6.4 哈夫曼树应用 —— 哈夫曼编码（对应课件 82-90 页）

哈夫曼编码是哈夫曼树的核心应用，用于数据压缩（将字符转换为 0/1 二进制流，减少传输 / 存储体积），课件分 “编码规则”“简单实例”“报文压缩实例” 三部分，老师结合计算过程详细讲解。

（1）哈夫曼编码规则

• 课件规定：在哈夫曼树中，左分支编码为 0，右分支编码为 1；
• 叶子结点的编码：从根结点到该叶子结点的 “路径上的 0/1 序列”（根到叶子的每一步分支对应的 0/1 依次拼接）。

（2）简单实例：权值 1、5、7、3 的哈夫曼编码

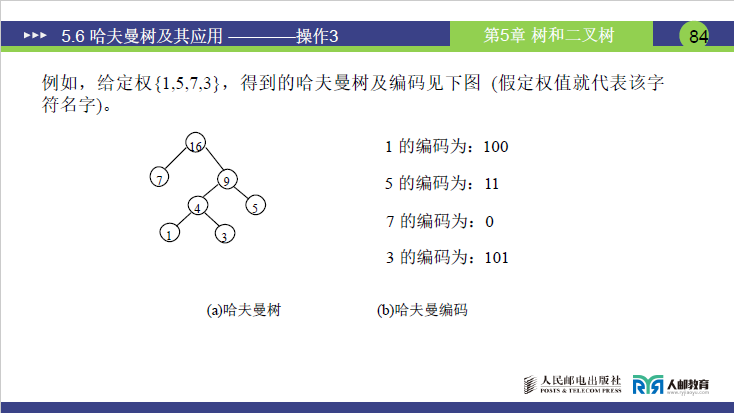
基于 5.6.3 构造的哈夫曼树，推导每个叶子（权值对应 “字符”）的编码：

• 权值 7 的叶子：根→7（左分支），路径为 “0”，编码：100；
• 权值 5 的叶子：根→9（右分支，编码 1）→5（右分支，编码 1），路径为 “11”，编码：11；
• 权值 3 的叶子：根→9（右分支，1）→4（左分支，0）→3（右分支，1），路径为 “101”，编码：101；
• 权值 1 的叶子：根→9（右分支，1）→4（左分支，0）→1（左分支，0），路径为 “100”，编码：100。

老师验证：编码长度与路径长度一致（如 7 的路径长度 1→编码长度 1，1 的路径长度 3→编码长度 3），符合 “权值大的编码短” 的特性，为后续压缩奠定基础。

（3）实际应用：报文压缩

以 “计算机传输需将字符转为 0/1 流” 为背景，对比 “等长编码” 与 “哈夫曼编码” 的压缩效果，验证哈夫曼编码的优越性。

步骤 1：统计字符频度

• 报文拆解：CAST、CAST、SAT、AT、A、TASA，共含字符：C、A、S、T；
• 频度统计（权值）：C 出现 2 次、A 出现 7 次、S 出现 4 次、T 出现 5 次（总次数：2+7+4+5=18）。

步骤 2：方案 1—— 等长编码

• 编码逻辑：4 个字符需至少 2 位二进制（1 位仅能表示 2 个字符），给每个字符分配 2 位等长编码：

  A:00、T:10、C:01、S:11；

• 总编码长度计算：每个字符编码长度为 2，总长度 =（各字符频度 × 编码长度）之和 =（2+7+4+5）×2=18×2=36。

老师分析：等长编码逻辑简单，但未考虑字符频度差异 —— 高频字符（A，7 次）与低频字符（C，2 次）编码长度相同，导致总长度冗余。

步骤 3：方案 2—— 哈夫曼编码（对应课件 87-90 页图：哈夫曼编码树）

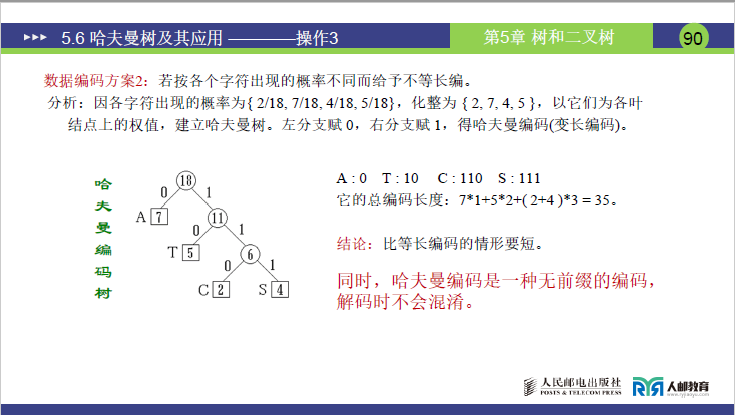
（1）构造哈夫曼树

以字符频度（2、4、5、7）为叶子权值，按 5.6.3 的规则构造哈夫曼树：

1. 初始森林：2、4、5、7；
2. 一次合并：2（左）+4（右）=6，森林变为 5、6、7；
3. 二次合并：5（左）+6（右）=11，森林变为 7、11；
4. 三次合并：7（左）+11（右）=18，得到哈夫曼树（对应课件 88 页图：根为 18，左子树 7 对应 A，右子树 11 分左 5 对应 T、右 6 分左 2 对应 C、右 4 对应 S）。

（2）生成哈夫曼编码

按 “左 0 右 1” 规则，推导各字符编码：

• A（权 7）：根→7（左），编码：0；
• T（权 5）：根→11（右，1）→5（左，0），编码：10；
• C（权 2）：根→11（右，1）→6（右，1）→2（左，0），编码：110；
• S（权 4）：根→11（右，1）→6（右，1）→4（右，1），编码：111。

（3）计算总编码长度

总长度 =（A 频度 ×A 编码长度）+（T 频度 ×T 编码长度）+（C 频度 ×C 编码长度）+（S 频度 ×S 编码长度）

= 7×1 + 5×2 + 2×3 + 4×3

= 7 + 10 + 6 + 12 = 35。

老师对比：哈夫曼编码总长度（35）＜等长编码（36），实现了数据压缩，且频度越高的字符（A）编码越短，压缩效率最优。

步骤 4：哈夫曼编码的关键优势 —— 无前缀编码

• 前缀编码定义：若一个字符的编码是另一个字符编码的 “前缀”（如 C 编码为 11，S 编码为 111，则 11 是 111 的前缀），解码时会混淆（接收 “111” 时，可能误判为 “C+1” 而非 “S”）。

• 哈夫曼编码特性：

  无前缀编码

  —— 任意一个字符的编码都不是其他字符编码的前缀：

  • A（0）：无其他编码以 “0” 开头；
  • T（10）：无其他编码以 “10” 开头；
  • C（110）：无其他编码以 “110” 开头；
  • S（111）：无其他编码以 “111” 开头。

• 强调：无前缀特性保证了解码的唯一性，接收方可按 “遇到完整编码就解码” 的规则还原字符，不会出现混乱（如接收 “0 10 110 111”，可直接解码为 “A T C S”）。

本课时总结

掌握哈夫曼树及其应用需完成四大核心任务：

1. 构造哈夫曼树：按 “选最小两树合并、左小右大” 规则，从叶子到根构建；
2. 生成哈夫曼编码：基于哈夫曼树，左 0 右 1，根到叶子的 0/1 序列即为编码；
3. 计算 WPL：所有叶子的 “权值 × 路径长度” 之和，验证树的最优性；
4. 理解应用场景：数据压缩（利用 “高频短码、低频长码” 减少总长度），且无前缀编码保证解码正确。

5.7 树、森林、二叉树的相互转换---操作4

本节核心逻辑与学习意义

数据结构是问题驱动型学科，树与森林是常见的多分支树形结构，但直接对其进行增删改查、遍历等操作的逻辑复杂度高、实现难度大。因此本节核心思路为：

1. 转换：将树 / 森林先转化为二叉树（利用二叉树成熟的操作体系）；

2. 处理：基于二叉树完成问题求解；

3. 还原：将处理后的二叉树转回原树 / 森林。

   本节所有知识点均围绕该核心思路展开，是连接多叉树与二叉树操作体系的关键桥梁。

5.7.1 树的表示法（课件页码 91-95）

树的表示法核心是解决 “如何存储树的结构关系”，共 4 种常用方式，结合具体树结构（课件图 5-xx，页码 91（a）树的结构）展开说明：

（1）双亲表示法

• 原理：用连续存储单元（数组）存放树中结点，每个结点含 2 个域：

  • data域：存储结点数据（如 A、B、C 等）；
  • parent域：存储该结点双亲在数组中的下标（根结点无双亲，设为 - 1）。

• 讲课补充示例

  （对应课件 91 页 “树的双亲表示法” 数组）：

  • 数组下标 0：data=A，parent=-1（A 是根，无双亲）；
  • 数组下标 1：data=B，parent=0（B 的双亲是 A，A 在下标 0）；
  • 数组下标 2：data=C，parent=0（C 的双亲是 A）；
  • 数组下标 3：data=D，parent=0（D 的双亲是 A）；
  • 数组下标 4：data=E，parent=1（E 的双亲是 B，B 在下标 1）；
  • 数组下标 5：data=F，parent=2（F 的双亲是 C，C 在下标 2）；
  • 数组下标 6：data=G，parent=2（G 的双亲是 C）；
  • 数组下标 7：data=H，parent=3（H 的双亲是 D，D 在下标 3）。

• 特点：找双亲方便（直接查parent域），找孩子需遍历整个数组。

（2）孩子表示法

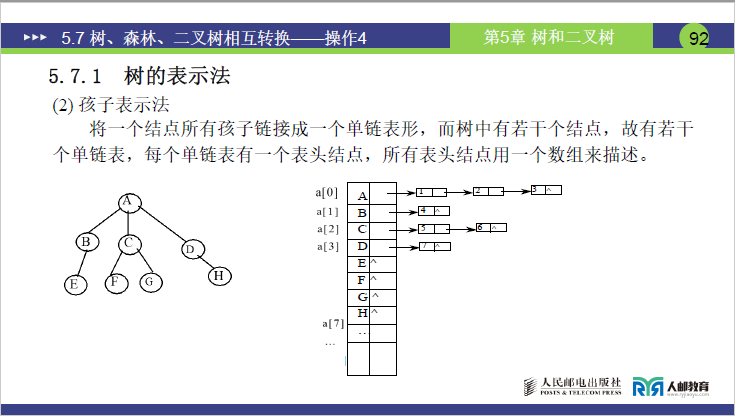
• 原理：分两步构建：

  1. 用数组存储所有结点（每个结点含data域和指向其孩子链表的指针）；
  2. 每个结点的所有孩子构成一个单链表（链表结点存储孩子在数组中的下标）。

• 讲课补充示例

  （对应课件 92 页孩子表示法示意图）：

  • 数组下标 0（A）：data=A，孩子链表指针指向链表结点 1→2→3（对应 B（1）、C（2）、D（3））；
  • 数组下标 1（B）：data=B，孩子链表指针指向链表结点 4（对应 E（4））；
  • 数组下标 2（C）：data=C，孩子链表指针指向链表结点 5→6（对应 F（5）、G（6））；
  • 数组下标 3（D）：data=D，孩子链表指针指向链表结点 7（对应 H（7））；
  • 数组下标 4-7（E、F、G、H）：无孩子，孩子链表指针为^（空）。

• 特点：找孩子方便（直接遍历孩子链表），找双亲需遍历所有孩子链表，效率低。

（3）双亲孩子表示法

• 原理：结合 “双亲表示法” 和 “孩子表示法”，每个结点同时存储parent域（找双亲）和孩子链表指针（找孩子）。
• 特点：兼顾找双亲、找孩子的需求，但存储开销更大（需同时存parent域和孩子链表指针）。

（4）孩子兄弟表示法

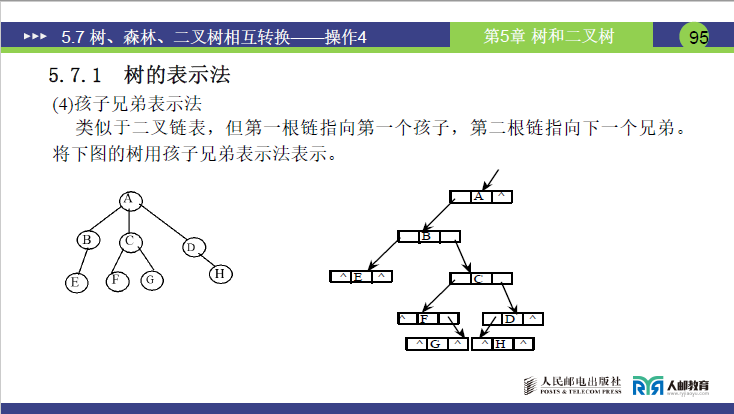
• 原理：采用类似二叉链表的结构，每个结点含 3 个域：
  • data域：存储结点数据；
  • leftChild（左指针）：指向该结点的第一个孩子；
  • rightSibling（右指针）：指向该结点的下一个兄弟（同一双亲的相邻兄弟）。
• 讲课补充示例（对应课件 94-95 页孩子兄弟表示法示意图）：
  • 根结点 A：data=A，leftChild指向第一个孩子 B，rightSibling为空（A 无兄弟）；
  • 结点 B：data=B，leftChild指向第一个孩子 E，rightSibling指向兄弟 C；
  • 结点 C：data=C，leftChild指向第一个孩子 F，rightSibling指向兄弟 D；
  • 结点 D：data=D，leftChild指向第一个孩子 H，rightSibling为空（D 是 A 的最后一个孩子）；
  • 结点 E：data=E，leftChild为空（无孩子），rightSibling为空（无兄弟）；
  • 结点 F：data=F，leftChild为空，rightSibling指向兄弟 G；
  • 结点 G：data=G，leftChild为空，rightSibling为空；
  • 结点 H：data=H，leftChild为空，rightSibling为空。
• 关键作用：是树 / 森林与二叉树转换的核心桥梁（将树的 “孩子 - 兄弟” 关系映射为二叉树的 “左 - 右” 指针关系）。

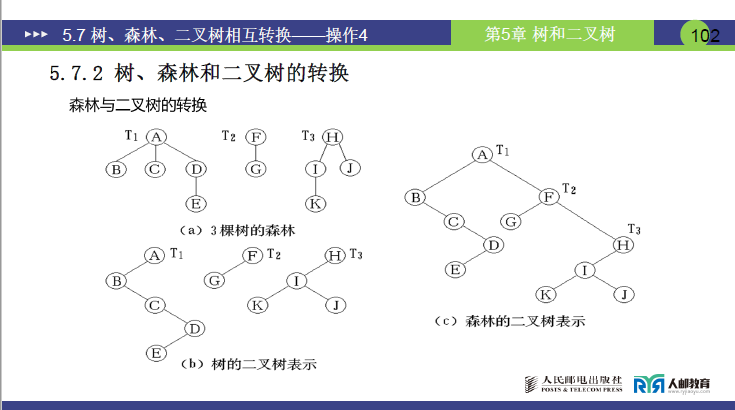
5.7.2 树、森林与二叉树的相互转换

（1）树转换为二叉树

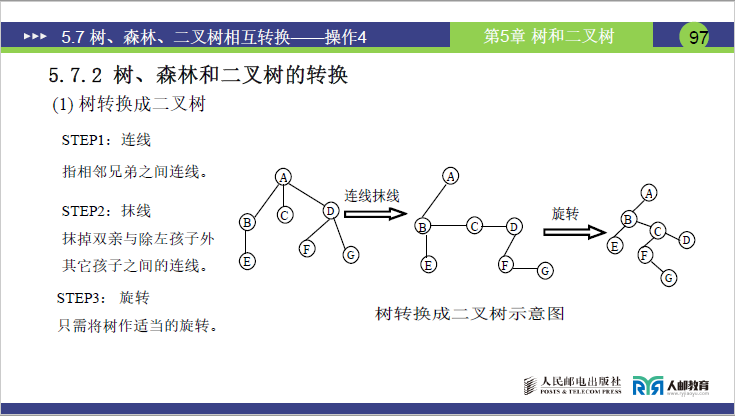
①核心规则（三步六字）

课件与讲课明确了 “连线→抹线→旋转” 的三步法，以下结合具体案例（根 A，孩子 B、C、D；B 的孩子 E）拆解：

a.连线：连接相邻兄弟

将同一双亲的所有相邻兄弟结点用线串联。

• 案例操作：将 B、C、D 三个兄弟结点依次连线，同时将 E 的兄弟（若有）连线（本例 E 无兄弟，无需操作）。

b.抹线：保留左孩子，删除其他亲子连线

仅保留双亲与最左孩子的连线，删除双亲与其他孩子的直接连线，让兄弟连线承担层级关联功能。

• 案例操作：仅保留 A→B 的连线，删除 A→C、A→D 的连线；保留 B→E 的连线（E 为 B 的最左孩子）。

c.旋转：调整为二叉树结构

将处理后的树顺时针旋转 45°，垂直方向的亲子分支转为二叉树左子树，水平方向的兄弟分支转为二叉树右子树。

• 案例结果：
  • A 的左孩子为 B，右孩子为NULL（根无兄弟）；
  • B 的左孩子为 E，右孩子为 C；
  • C 的左孩子为NULL（无最左孩子），右孩子为 D；
  • D 的左、右孩子均为NULL。

②转换本质

树转二叉树后，仅存在左子树（孩子），无右子树（根无兄弟），所有兄弟结点通过右指针串联，实现了多叉树到二叉树的降维。

（2）森林转换为二叉树

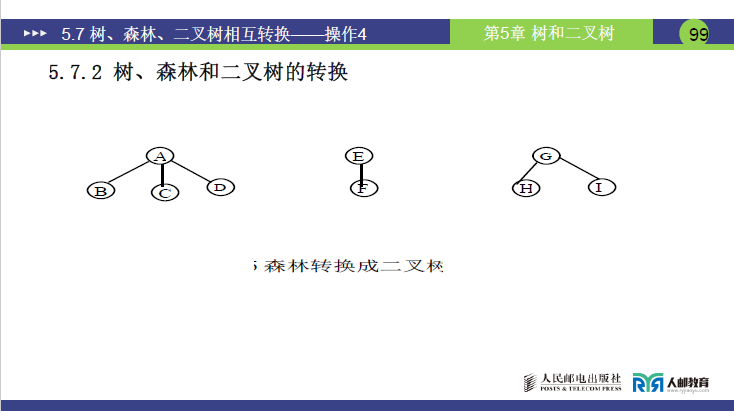
森林是 “m 棵互不相交的树的集合”，其转二叉树分为两步，结合课件 “T1、T2、T3 三棵树的森林” 案例拆解：

①分步转换：每棵树转二叉树

将森林中的 T1、T2、T3 分别按 “树转二叉树” 的三步法，转为 3 棵独立二叉树（记为 B1、B2、B3），且每棵二叉树均 “只有左子树，无右子树”。

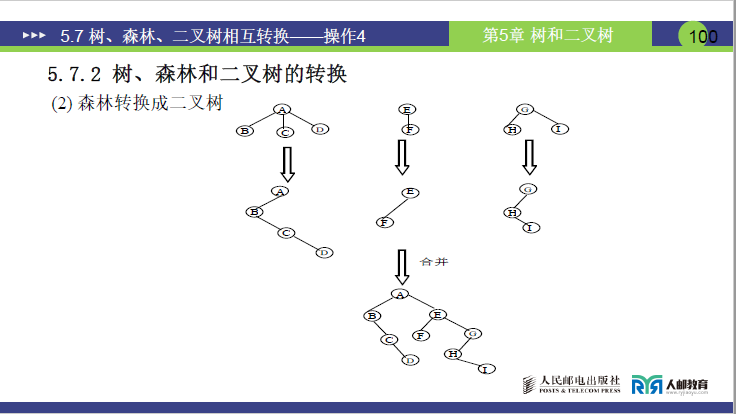
②合并连接：右子树串联多棵二叉树

将第 n 棵二叉树接入第 n-1 棵的右子树，依次向前合并，最终形成一棵完整二叉树。

• 案例操作：
  1. 将 T3 对应的 B3 接入 T2 对应的 B2 的右子树；
  2. 将合并后的 B2-B3 接入 T1 对应的 B1 的右子树；
  3. 最终 B1 为根，其右子树为 B2，B2 的右子树为 B3，形成森林对应的二叉树。

（3）二叉树还原为树 / 森林

为 “树 / 森林转二叉树” 的逆操作，核心是断开右链、还原亲子关系，步骤如下：

①断右链：拆分森林中的独立树

将二叉树根结点及所有结点的右指针链断开，拆分出 m 棵 “无右子树的二叉树”，每一棵对应原森林中的一棵树。

• 课件案例：某森林对应的二叉树，断开右链后得到 4 棵无右子树的二叉树，对应原森林的 4 棵树。

② 二叉树还原为树：逆三步法

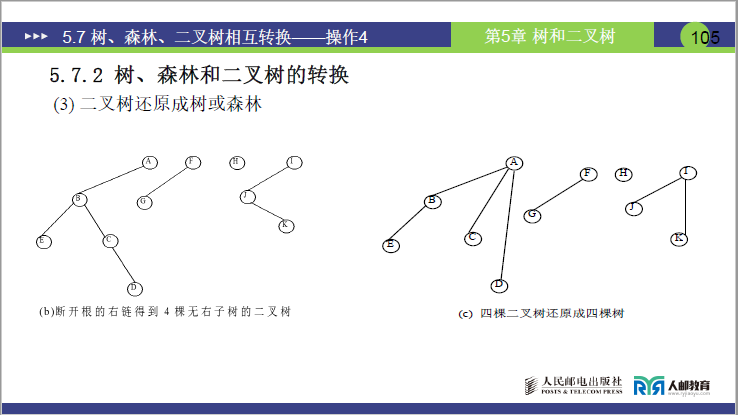
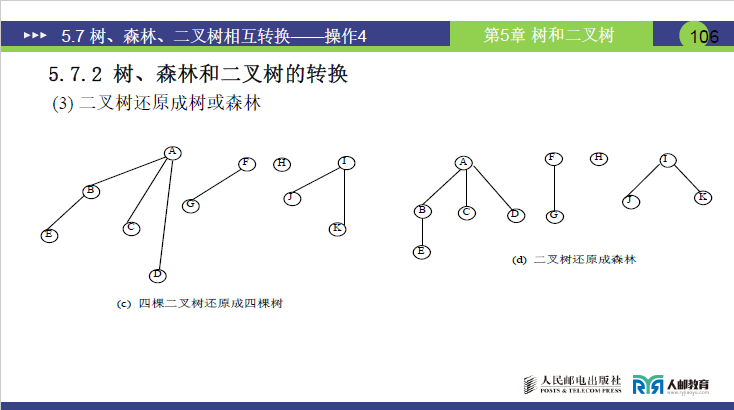
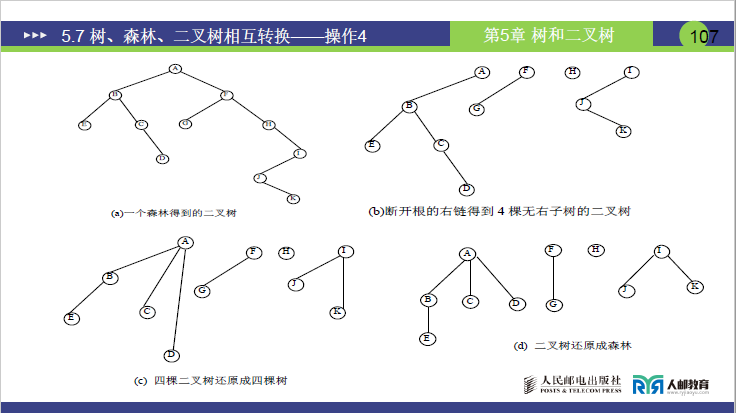
对每棵拆分后的二叉树，执行 “加线→抹线→调整” 的逆操作：

a.加线：重建亲子连线

将右指针指向的 “兄弟结点” 与共同双亲重新建立亲子连线。

b.抹线：删除兄弟连线

断开右指针的兄弟关联，恢复树的亲子层级。

c.调整：恢复树的层级结构

将二叉树的左右分支结构调整为树的 “同一层孩子” 结构（所有孩子结点平行排列，无左右之分）。

• 案例结果：课件中 4 棵二叉树还原后，形成一棵 “根 A，孩子 B、C、D、E” 的树，及另外 3 棵独立树，恢复为原森林结构。

5.7.3 树和森林的遍历

树 / 森林的结点可有多棵子树，无明确 “中序” 定义（无法区分 “左 - 根 - 右” 的中间位置），因此仅支持先序遍历和后序遍历，且其遍历结果与对应二叉树的遍历结果存在固定映射。

（1）树的遍历

①先序遍历

• 规则：根结点→依次先序遍历各子树；
• 课件案例：树 “根 A，孩子 B、C；B 的孩子 E” 的先序遍历为A→B→E→C。

②后序遍历

• 规则：依次后序遍历各子树→根结点；
• 课件案例：上述树的后序遍历为E→B→C→A。

（2）森林的遍历

①先序遍历

• 规则：第一棵树的先序遍历→第二棵树的先序遍历→…→第 m 棵树的先序遍历；
• 课件案例：森林 {T1（根 A，孩子 B）、T2（根 C，孩子 D）} 的先序遍历为A→B→C→D。

②后序遍历

• 规则：第一棵树的后序遍历→第二棵树的后序遍历→…→第 m 棵树的后序遍历；
• 课件案例：上述森林的后序遍历为B→A→D→C。

（3）与二叉树遍历的映射关系（核心考点）

讲课与课件明确了以下等价关系，可简化树 / 森林的遍历操作：

1. 树 / 森林的先序遍历 = 对应二叉树的先序遍历；
   • 验证：上述树的先序（A→B→E→C），对应二叉树先序结果一致；
2. 树 / 森林的后序遍历 = 对应二叉树的中序遍历；
   • 验证：上述树的后序（E→B→C→A），对应二叉树中序结果一致。

本节关键结论与易错点

1. 孩子兄弟表示法是树与二叉树转换的唯一媒介，其 “左孩子右兄弟” 的逻辑是降维核心；
2. 树转二叉树后无右子树，森林转二叉树后右子树为其他树的根；
3. 树 / 森林的后序遍历≠对应二叉树的后序遍历，而是等价于中序遍历，为考研高频易错点。

参考资料：教材《数据结构 C 语言 第 3 版》 数据结构考研指导（基础篇） 、数据结构考研指导（基础篇） 视频课程｜赵海英