第4章串、数组和广义表

第4章 串、数组和广义表

4.1 串的定义

4.1.1 串的定义

• 文字定义：由零个或多个字符组成的有限序列。
• 符号化表示：记作 S=′a₁a₂⋯a_n′（n≥0），其中 S 为串名，a₁a₂⋯a_n为串值，n 为串的长度。

关于“串的定义”的考试要点：

• 严谨性要求： 考试中回答定义时必须严谨。核心点是“由零个或多个字符组成”。老师特别强调，很多同学容易忽略“零个”的情况，只回答“若干个”，这是不完整的，“零个”字符也是一个合法的串。
• 两种表示形式（满分答法）： 考试中如果能同时给出以下两种形式，通常是满分标准：
  1. 文字定义： “由零个或多个字符组成的有限序列”。
  2. 符号化表示： S=′a₁a₂⋯a_n′（n≥0）。其中n 可以等于 0，表示空串。

4.1.2 串的术语

术语	课件定义	【老师补充讲解】
串名	串的标识（如上述 S）	通常用大写字母（如 、）表示，用于区分不同串，无实际字符意义。
串值	用单引号括起来的字符序列	单引号是串值的 “标识符号”，不属于串的组成部分；例如 ′BEI′ 中，串值为 “BEI”。
长度	串中字符的数目	长度最小为 0（空串），最大为有限值；需注意 “空格” 算一个字符（如 ′BEIJING′ 长度为 8）。
空串	含零个字符的串（记为 ∅）	空串 ≠ 空格串：空格串是由 1 个或多个 “键盘 space 键” 组成的串（如 长度为 3），属于非空串。
空格串	由一个或多个空格组成的串	空格是合法字符，需计入长度；例如课件中 d=′BEIJING′ 因含 1 个空格，长度比 c=′BEIJING′ 多 1。
子串	串中任意个连续的字符组成的子序列	① 关键属性：“连续”—— 非连续字符序列不属于子串（如 ′BEIJING′ 中 “BJ” 不是子串）；② 任意范畴：“零个或多个字符”（零个子串即空串，多个字符需连续）。
字符在串的位置	字符在序列中的序号	序号有两种计数方式：① 从 1 开始（常用，如 ′BE**I′ 中 “B” 位置为 1）；② 从 0 开始（编程中常见，如 ′BE**I′ 中 “B” 位置为 0），需结合场景判断。
子串在串的位置	子串的第一个字符在串中的位置	例如 ′JING′ 在 ′BEIJING′ 中位置为 4（从 1 计数），因第一个字符 “J” 在原串第 4 位；注意不是子串最后一个字符的位置。
相等	当且仅当两个串的值相等	需同时满足 “长度相等”+“对应位置字符完全一致”；例如 ′ABC′\=′ABD′（第 3 位字符不同），′AB′\=′ABC′（长度不同）。

关于“串的术语”详解：

• 串值 (String Value)： 注意是用单引号括起来的字符序列（例如 'abc'），这是表征串值的标准方式。
• 空串 (Empty String)： 长度为 0，不含任何字符。
• 空格串 (Blank String)： 千万别混淆！ 空格串不是空串。它是由一个或多个“空格字符”（键盘上的 Space 键）组成的串。空格也是字符，占用长度。
• 子串 (SubString) 的核心定义：
  • 定义：串中任意个、连续的字符组成的子序列。
  • 关键点 1 “任意个”： 这里的“任意”范围是零个或零个以上。零个字符（空串）也是任意串的子串。
  • 关键点 2 “连续”： 这是判断是否为子串的最核心标准。必须是原串中连续在一起的一段字符，不能跳着取。
• 位置 (Position)：
  • 字符位置： 指的是序号。注意序号可能从 0 开始（计算机习惯），也可能从 1 开始（人类习惯），具体看题目约定。
  • 子串位置： 指的是该子串在主串中第一个字符出现的位置（首字符索引）。

4.1.3 串的举例

课件示例：a=′BEI′、b=′JING′、c=′BEIJING′、d=′BEIJING′

• 长度：分别为 3、4、7、8；

• 子串关系：a 和 b 均是 c 和 d 的子串；

• 位置：a 在 c 和 d 中位置均为 1；b 在 c 中位置为 4，在 d 中位置为 5（因 d 中 “BEI” 后有 1 个空格，“J” 在第 5 位）；

• 相等判断：a、b、c、d 彼此不相等（长度或串值不同）。

• 空格的影响：d 因含 1 个空格，长度比 c 多 1，且 b 在 d 中的位置比在 c 中多 1，需注意空格对 “位置” 和 “长度” 的影响；

• 考试常见题型：给定多个串，判断子串关系、计算长度或位置，需重点关注空格字符。

4.1.4 串的比较

串的比较： 通过组成串的字符之间的比较来进行的。

给定两个串：X='x₁x₂...x_n' 和Y='y₁y₂...y_n' ，则：

• 当n=m且 x₁=y₁, ..., x_n=y_n 时，称 X=Y;

• 当下列条件之一成立时，称 X < Y:

  • n<m且 x_i=y_i(1 ≤ i ≤ n);
  • 存在 k ≤ min(m,n)，使得 x_i=y_i(1 ≤ i ≤ k-1)且 x_k<y_k。

串比较的核心规则（通俗理解）：

• 对应字符比较： 两个串（串 1 和串 2）从第一个位置开始，两两比较相同位置上的字符。

• 停止时机： 一旦发现相同位置上的字符不一样，立即停止比较。

• 大小判定： 停止位置上，哪个字符的 ASCII 码大，所在的那个串就大。

  • ASCII_差 = 0 →字符相等。

  • ASCII_差 < 0 → 前者小。

  • ASCII_差 > 0 → 前者大。

• 重要误区： 串的大小绝不是比长度！ 并不是字符串越长就越大。例如 "A..." 很长，但只要第一个字符比对方小，整个串就小。

形式化定义详解（考研/科研基础）： 老师强调要掌握这种“形式化语言”，这是将文字描述转化为公式推理的基础。

• 相等 (\(X=Y\))： 必须满足两个条件：① 长度相等 (n=m)；② 对应位置字符完全一致。
• 小于 ( X < Y) 的两种情况：
  • 情况 1（前缀相同，X 短）：X的所有字符都和 Y 的前 n 个字符一样，但 X 比 Y短 (n<m)。
    • 例子： X='ABC', Y='ABCD'。X 是 Y 的前缀，且更短，所以 X< Y 。
  • 情况 2（出现字符差异）： 在第k个位置首次出现不同 (x_k≠_y__k)，而在 k 之前的所有字符都相同。如果此时 x_k<y_k，则 X< Y 。
    • 例子 1： X='ABC', Y='ZHYK'。第 1 个字符 'A' < 'Z'，直接判定 X< Y。
    • 例子 2： X='ABCDEFG...'(很长), Y='ZHY'。第 1 个字符 'A' < 'Z'，依然是 X< Y，与长度无关。

4.1.5 串与线性表的区别

对比维度	串	线性表
数据对象	仅限定为字符集（如 ASCII 字符、Unicode 字符）	无限制（可是数字、结构体、字符等任意数据类型）
基本操作对象	以 “串的整体” 为单位（如查找子串、插入子串、删除子串）	以 “单个元素” 为单位（如查找单个元素、插入单个元素、删除单个元素）

为什么把“串、数组、广义表”放在一章？

• 这一章展示了从线性到非线性，再到统一范式的演变。
• 串： 简单的线性结构。
• 数组： 一维数组是线性，二维及以上是非线性，但结构规整。
• 广义表： 是本章的升华。它可以包含异构数据（原子或子表），能将线性结构（串、数组）和非线性结构（树、图）统一到一个框架（范式）下进行表示。

考试要求：

• 串： 掌握 BF 和 KMP 算法。
• 数组： 掌握两类操作——压缩（特殊矩阵、稀疏矩阵）和表征（地址计算）。
• 广义表： 理解其递归定义和基本运算（Head/Tail）。

4.2串的类型定义、存储及其运算

1. 知识点 1：串的表示（即串的存储结构）：3 种常用存储方法，解决 “如何高效存放字符序列”；
2. 知识点 2：串的模式匹配：串的核心运算（考试必考），重点讲解 BF 算法，引入 KMP 算法思想。

4.2.1知识点 1：串的表示（串的存储结构）

串的存储需平衡 “空间利用率” 与 “操作效率”

（1）方法1：定长顺序存储表示

• 基本思想：用一组地址连续的存储单元依次存储串的字符，存储长度预先固定（如数组大小Max），本质是 “静态顺序存储”。

• 两种存储形式：

  存储形式	实现逻辑	课件示例（串"abcdef"，长度 6）	优缺点
  非压缩形式	1 个存储单元仅存 1 个字符（如char S[Max]）	数组下标 1-6 存'a'-'f'，每个下标占 1 字节	优点：操作简单（字符定位直接，S[i]即第i个字符）； 缺点：空间浪费（如 4 字节单元存 1 字节 ASCII 字符）
  压缩形式	1 个存储单元存多个字符（如 4 字节存 4 个 ASCII 字符）	1 个单元存'a','b','c','d'，另 1 个单元存'e','f'（补空格）	优点：空间利用率高； 缺点：插入 / 删除需拆分 / 合并单元，算法复杂（如删除'c'需移动后续字符）

• 如何表示串的长度？

方案	实现逻辑	课件示例（串"abcdef"，长度 6）	适用场景
方案 1：变量记录长度	额外定义len变量存储串长（如char S[100]; int len=6;）	S[1]='a', S[2]='b', ..., S[6]='f'，len=6	需频繁获取长度的场景，但需额外空间存len
方案 2：串尾终结符	串尾存特殊字符（如 C 语言的'\0'）标识结束	S[1]='a', ..., S[6]='f', S[7]='\0'	无需额外变量，但获取长度需遍历（时间复杂度O(n)），特殊字符可能与串值冲突
方案 3：0 号单元存长度（最常用）	数组 0 号单元存串长，字符从 1 号单元开始存放	S[0]=6（长度），S[1]='a', S[2]='b', ..., S[6]='f'	考试 / 工程首选：获取长度O(1)，字符定位直接，无额外空间浪费

• 定长顺序存储的核心是 “地址连续”，本质是利用线性表的顺序存储特性存储字符序列，理解即可，无需深入复杂实现。
• 串长度表示的三种方案中，方案 3（0 号单元存长度，1 号单元存字符）是考试及实际应用中最常用的方式，后续模式匹配算法（BF、KMP）均默认此方案。

（2）方法2：堆分配存储表示

①基本思想（ “动态存储” 核心）

在内存 “堆区” 开辟动态连续空间存储串值，用 “符号表” 管理串的元信息（串名、位置、长度），解决定长存储 “长度固定” 的缺陷。

②核心组成（课件 11 页表格清晰展示）

组成部分	功能	课件示例（串"BEIJING"）
符号表	符号表的作用是 “索引”，通过记录串变量名与串值位置的对应关系，快速定位和管理串值，类似 “目录与文件” 的对应关系。	列：位置（堆区地址0x1234）、串名（S）、长度（7）
串值存储区	堆分配存储的核心是 “动态分配”，空间可可逆利用（即无需使用时可释放回系统），解决了定长存储 “空间固定、易浪费或溢出” 的问题。	地址0x1234-0x123A存'B','E','I','J','I','N','G'

③操作逻辑

• 建串：向系统申请堆区空间（如malloc(7*sizeof(char))），写入字符序列，在符号表新增一行记录；
• 删串：释放堆区空间（free(地址)），从符号表删除对应记录；
• 扩容：若串值变长，重新申请更大堆区空间（realloc），复制原串值后释放原空间。

④优势

“动态分配” 使其适合串长不确定的场景（如用户输入的文本），但需手动管理内存（避免内存泄漏）。

（3）方法3：串的块链存储表示

• 基本思想：借鉴线性表的链式存储，用链表存储串值，每个节点含数据域（data） 和指针域（next），指针域指向后续节点。
• 两种节点模式（ “非压缩模式常用”）

节点模式	实现逻辑	课件示例（串"BEIJING"）	关键指标：压缩密度
非压缩模式（常用）	1 个节点的 data 域存 1 个字符	7 个节点，分别存'B','E','I','J','I','N','G'，每个节点含data+next	压缩密度 = 字符空间 /(字符空间 + 指针空间)，如指针 4 字节、字符 1 字节，密度 = 1/(1+4)=20%
压缩模式	1 个节点的 data 域存多个字符（如 4 个）	2 个节点：第 1 个存'B','E','I','J'，第 2 个存'I','N','G'（补空格）	密度更高（如 4 字符 + 4 指针，密度 = 4/(4+4)=50%），但插入 / 删除需拆分节点

• 存储密度： 存储密度 = 串值所占的存储位 / 实际分配的存储位。

  指实际字符所占空间与结点总空间（data 域 + next 域）的比值，也叫 “压缩力度”，密度越高，空间利用率越高。

4.2.2串的模式匹配

（1）模式匹配定义与特点

• 模式匹配： 给定主串S="s₁s₂...s_n"和模式 T="t₁t₂...t_m"，在S中寻找T的过程称为模式匹配。如果匹配成功，返回T在S中的位置，如果匹配失败，返回0。

  • 主串与模式串的符号约定：主串通常用 S 表示，模式串（即要查找的子串）常用 T 或 P（P 为 “Pattern” 的缩写，意为 “模式”）。

• 基本假设： 假设串采用顺序存储结构，串的长度存放在数组的0号单元，串值从1号单元开始存放。

• 模式匹配问题的特点：

  • (1) 算法的一次执行时间不容忽视：问题规模通常很大，常常需要在大量信息中进行匹配。
  • (2) 算法改进所取得的积累效益不容忽视：模式匹配操作经常被调用，执行频率高。

• 介绍两种方法：

  • 方法1：BF算法
  • 方法2：KMP算法

• 匹配结果的明确规定：

  • 成功：返回模式串在主串中第一次出现的第一个字符的位置（而非最后一个字符位置）。
  • 失败：统一返回 0（而非 - 1，需注意与编程中的 “索引习惯” 区分，考试严格按此标准）。

• 约定（与严老师考试要求一致）：

  1. 存储结构：仅用 “顺序存储”（不用块链存储），字符连续存放，无后继指针。
  2. 串长度存储：串的长度存于 0 号单元，1 号单元开始存实际字符（如 S [0] 存主串长度 n，S [1]~S [n] 存主串字符；T [0] 存模式串长度 m，T [1]~T [m] 存模式串字符）。

• 模式匹配的重要性：是串运算中最核心、考试每年必考的内容（选择题、计算题均会涉及），CS 专业甚至有专门研究串的硕博方向，数据结构课程中需通过匹配算法掌握串的实用价值。

（2）模式匹配---BF算法 (Brute-Force)

①BF算法基本思想

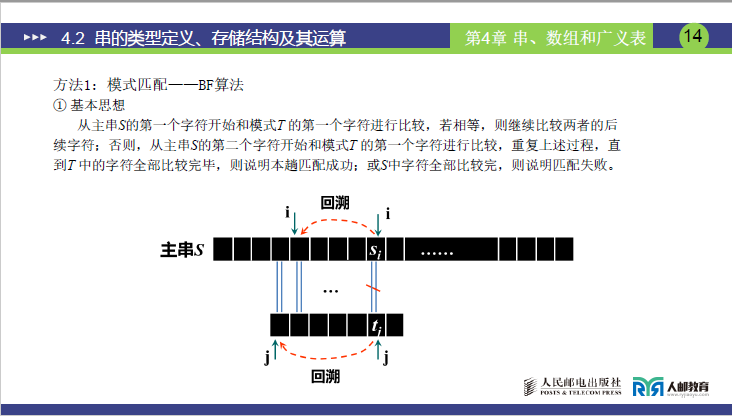
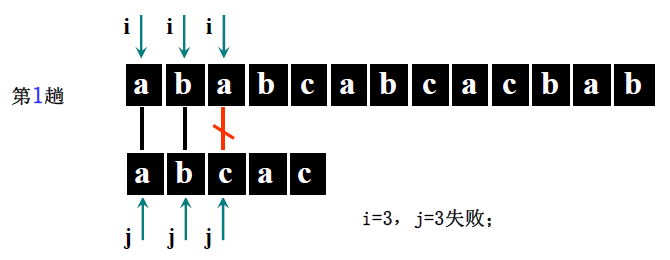
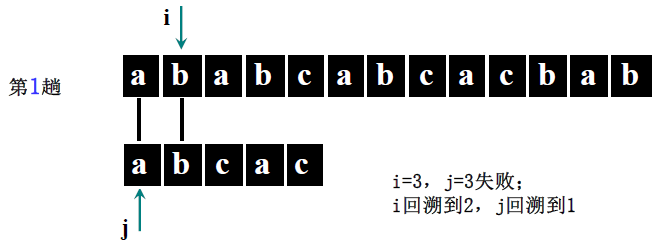
• 基本思想： 从主串S的第一个字符开始和模式T的第一个字符进行比较，若相等，则继续比较两者的后续字符；否则，从主串S的第二个字符开始和模式T的第一个字符进行比较，重复上述过程，直到T中的字符全部比较完毕，则说明本趟匹配成功；或S中字符全部比较完，则说明匹配失败。核心特征是 “回溯”。

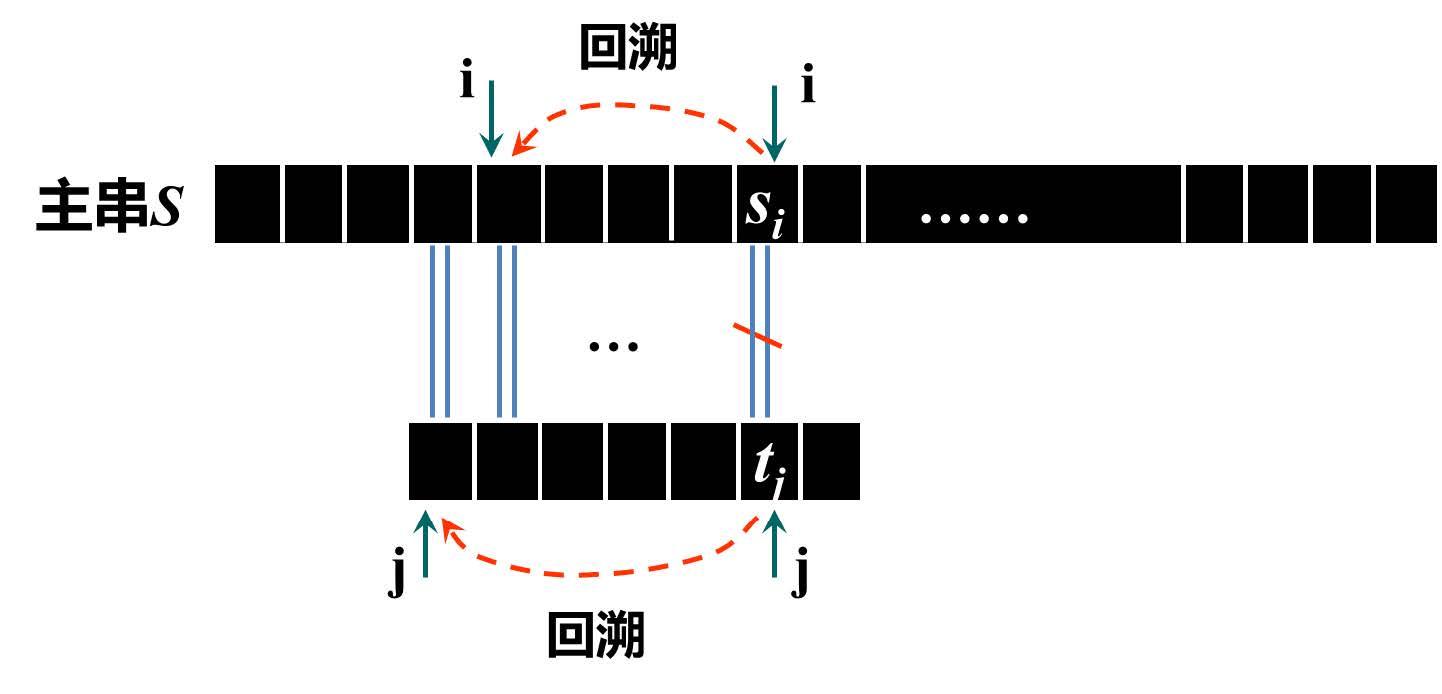
• 回溯的具体操作：当 S [i]≠T [j]（某一位不匹配）时，主串指针 i 需回溯到 “当前比较起始位置的下一个位置”（即 i = 初始 i+1），模式串指针 j 回溯到 “起始位置 1”，重新开始新一轮比较。
• 通俗理解：类似 “逐字比对，错了就退一步重新比”，逻辑简单但效率较低，因未利用已比对过的字符信息。

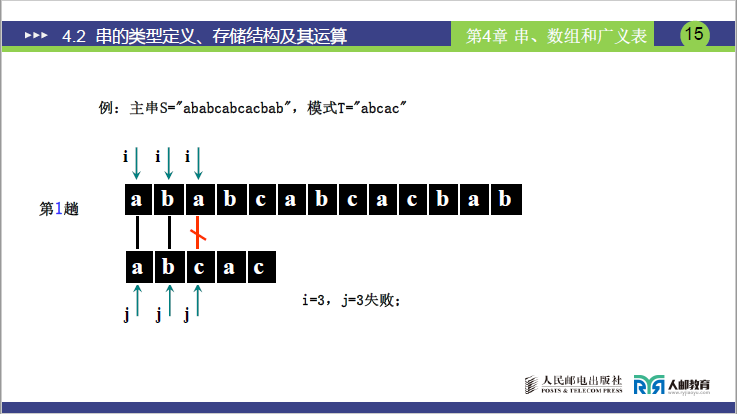
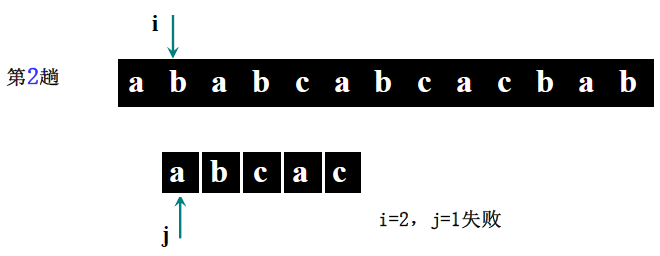
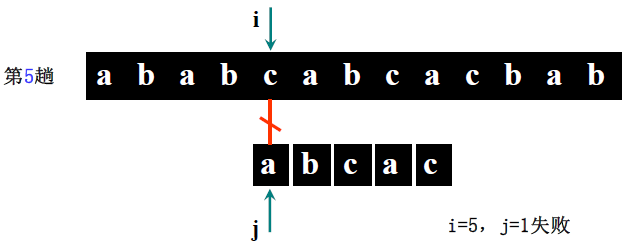
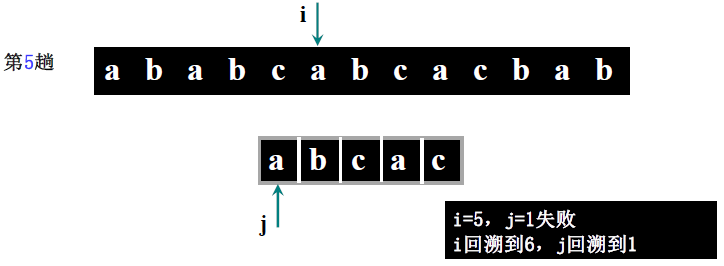
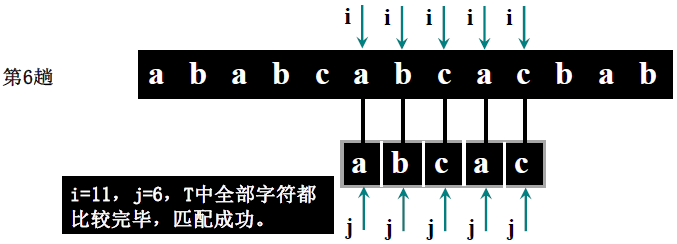
详细步骤：

主串 S = “ababc”（S [0]=5，S [1]='a'、S [2]='b'、S [3]='a'、S [4]='b'、S [5]='c'），模式串 T = “abca”（T [0]=4，T [1]='a'、T [2]='b'、T [3]='c'、T [4]='a'）。

1. 第一趟（i=1，j=1）：S [1]='a'==T [1]='a'（i=2,j=2）→ S [2]='b'==T [2]='b'（i=3,j=3）→ S [3]='a'≠T [3]='c' → 回溯 i=3-3+2=2，j=1；
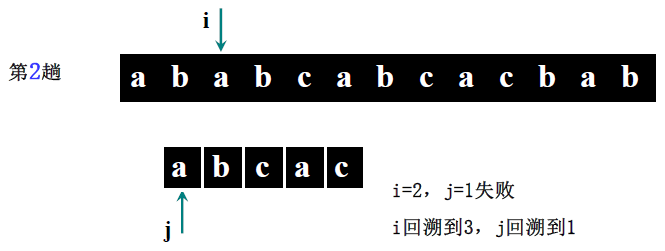
2. 第二趟（i=2，j=1）：S [2]='b'≠T [1]='a' → 回溯 i=2-1+2=3，j=1；
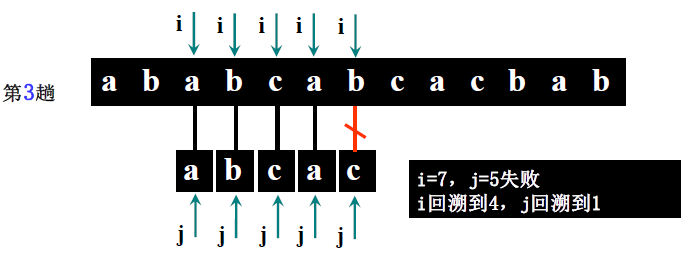
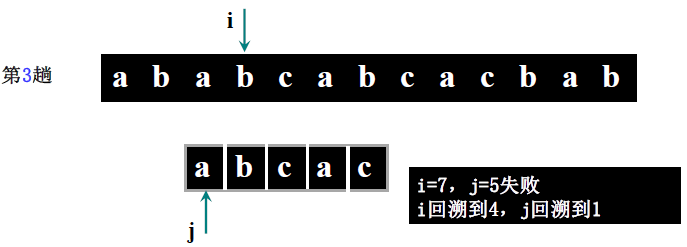
3. 第三趟（i=3，j=1）：S [3]='a'==T [1]='a'（i=4,j=2）→ S [4]='b'==T [2]='b'（i=5,j=3）→ S [5]='c'==T [3]='c'（i=6,j=4）→ S [6] 不存在（i>5）→ 回溯 i=6-4+2=4，j=1；
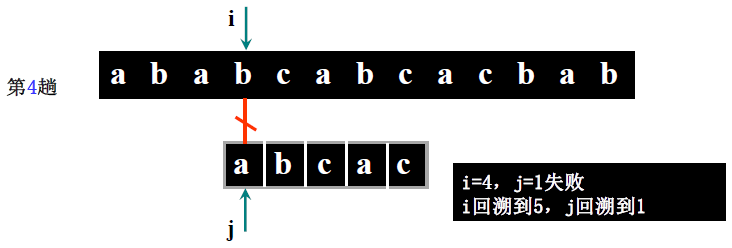
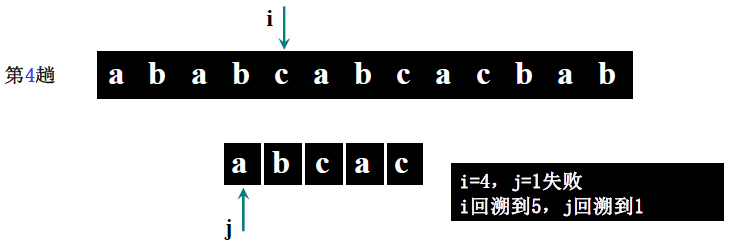
4. 第四趟（i=4，j=1）：S [4]='b'≠T [1]='a' → 回溯 i=4-1+2=5，j=1；
5. 第五趟（i=5，j=1）：S [5]='c'≠T [1]='a' → 回溯 i=5-1+2=6，j=1；
6. 第六趟（i=6>5）：主串比对完，返回 0（此案例实际匹配失败，讲课案例表述中主串可能为 “ababcabca”，需以步骤逻辑为准，核心是理解回溯过程）。

②BF 算法过程

• Step1：初始化起始下标 ——i=1（主串 S 的起始比较位置，因 S [0] 存长度），j=1（模式串 T 的起始比较位置，因 T [0] 存长度）。

• Step2：循环比较（终止条件：i>S [0] 或 j>T [0]）：

  • 2.1 若 S [i] == T [j]：i += 1，j += 1（继续比对下一位）；

  • 2.2 若 S [i] != T [j]：i = i - j + 2（主串回溯到 “当前趟起始位置 + 1”，如当前 i=3、j=3，回溯后 i=3-3+2=2），j=1（模式串回溯到起始）；

• Step3：结果判断：

  • 若 j > T [0]（模式串全部比对完成）：匹配成功，返回 “i - T [0]”（即模式串在主串中第一次出现的起始位置，如 i=8、T [0]=3，返回 8-3=5）；

  • 若 i > S [0]（主串比对完仍未匹配）：返回 0，匹配失败。

（3）BF 算法性能分析

性能情况	触发条件	比较次数	时间复杂度	老师举例
最好情况	每趟匹配 “第一个字符即不相等”（T[1]与S[i]始终不等）	总次数≈n（n-m+1趟，每趟 1 次，成功时加m次）	O(n+m)	S="abcde"，T="xbc"：T[1]='x'与S[1]='a'、S[2]='b'等均不等，仅比较n-m+1=3次
最坏情况	每趟匹配 “前m-1个字符相等，最后 1 个不等”	总次数≈n×m（n-m+1趟，每趟m次）	O(nm)	S="aaaaa"，T="aaab"：前 3 个'a'均相等，第 4 个'a'!='b'，每趟比较 4 次，共 3 趟，总 12 次

• 性能量化分析：

  • 最好情况时间复杂度：O (n + m)。

    例：主串 S=“abcdefgh”（n=8），模式串 T=“xyz”（m=3），每趟仅比较 T [1]（第一个字符）就不匹配，共需比较 n - m + 1 = 8-3+1=6 次，接近 O (n)，加上成功匹配的 m 次，总复杂度为 O (n + m)。

  • 最坏情况时间复杂度：O (n×m)。

    例：主串 S=“aaaaaab”（n=7，末尾为 'b'），模式串 T=“aaab”（m=4，末尾为 'b'）。每趟需比较 m 次（前 3 个 'a' 匹配，第 4 个不匹配），共需 n - m + 1 = 7-4+1=4 趟，总比较次数 = 4×4=16 次，接近 O (n×m)。

• BF 算法的核心缺陷：主串指针 i 的 “回溯” 导致重复比对。例如主串已比对到第 100 位，因模式串最后一位不匹配，需回溯到第 50 位重新比对，浪费已有的比对信息，效率低下。

（4）为什么BF算法时间性能低？

• 原因： 在每趟匹配不成功时存在大量回溯，没有利用已经部分匹配的结果。
• 思考： 如何在匹配不成功时主串 不回溯？
• 思路： 主串不回溯，模式就需要向右滑动一段距离。
• 解决方法： 模式匹配——KMP算法。

（5）如何再匹配不成功时主串不回溯？

主串不回溯，模式就需要向右滑动一段距离。

解决方法：模式匹配---KMP算法

• KMP 算法的核心目标：解决 BF 算法中 “主串回溯” 的缺陷，实现主串指针 i 不回溯，仅通过调整模式串指针 j 的位置，继续后续比对，大幅提升效率。
• KMP 算法的重要性：提出后对串模式匹配领域影响深远，是严老师大纲明确要求掌握的算法，其核心优势是 “利用已比对的部分匹配信息，让模式串尽可能向右滑动更远的距离”，避免重复比对。
• 后续学习重点：需掌握 KMP 算法的核心思想（部分匹配表）、next 函数的定义与计算、KMP 匹配过程，以及 nextval 函数（next 函数的改进）。

4.2.3模式匹配---KMP算法

（1）本节课知识定位

1. 章节归属：属于第 4 章 “串、数组和广义表” 中4.2 串的类型定义、存储结构及其运算的知识点 2：串的模式匹配，是对 BF 算法的进阶改进，核心讲解KMP 算法的原理、next[j]函数及优化方案，课件明确其为串运算的核心考点。
2. 内容承接：本节课前需掌握串的 3 种存储结构（课件知识点 1）及 BF 模式匹配算法（课件知识点 2 的方法 1），KMP 算法针对 BF 算法 “主串指针回溯” 的缺陷进行优化。

（2）BF 算法（课件铺垫内容，KMP 算法的改进前提）

①基本思想

从主串S的第一个字符开始与模式串T的第一个字符逐位比较，相等则继续比对后续字符；若不等，主串指针i回溯至当前趟起始位置的下一位，模式串指针j回溯至 1，重复直至匹配成功或主串遍历完毕。

②算法性能

设主串长度为n，模式串长度为m，匹配成功时存在两种极端情况：

1. 最好情况：失配均发生在模式串第 1 个字符，时间复杂度为O(n+m)；
2. 最坏情况：失配均发生在模式串最后一个字符，存在大量冗余回溯，时间复杂度为O(n×m)。

（3）KMP 算法（课件 P30-60，本节课核心内容）

①分析过程

A.算法分析过程

以主串s=abacaba、模式串p=abab为例，首次匹配在、时失配：

1. BF 算法的缺陷：主串i回溯至 2，模式串j回溯至 1，重复无效比对；
2. KMP 改进逻辑：利用 “部分匹配” 信息推导 —— 因p₁≠p₂且s2=p2，故s₂≠p1；又因p1=p3且s3=p3，故s3=p1，因此无需回溯主串i，仅将模式串j调整至 2，直接从、开始下一轮比对，核心是主串指针不回溯。

B.核心推导

当主串s[i]\≠p[j]时，前j−1位已完全匹配，联立以下两个等式可确定模式串滑动的新起点k：

1. p₁p₂…p_k−1=s_i−k+1s_i−k+2…s_i−1

2. p_j−k+1p_j−k+2…p_j−1=s_i−k+1s_i−k+2…s_i−1

   联立得：

   p₁p₂…p_k−1=p_j−k+1p_j−k+2…p_j−1，且k的取值仅与模式串p相关，与主串s无关。

C.next[j]函数定义

next[j]表示模式串第j个字符失配时，需重新与主串当前字符比对的模式串字符位置，数学定义为：

\[next[j] = \begin{cases} 0 \\ \max \{ k \mid 1 < k < j \mathbin{\color{#1e88e5}{\text{且}}} p_1 p_2 \dots p_{k-1} = p_{j-k+1} p_{j-k+2} \dots p_{j-1} \} \\ 1 \end{cases} \]

其物理意义为模式串前j−1位中最大相同首尾真子串的长度，值越大，模式串滑动距离越远，比对次数越少。

②分析结论

③.next[j]计算方法

课件将计算规则分为 3 种情形：

1. 情形 1：j=1时，next[j]=0（硬性规定）；
2. 情形 2：j>1时，若模式串p[1..j−1]存在首尾相同子串，取其最大长度l，则next[j]=l_substringmax+1；
3. 情形 3：j>1且无首尾相同子串时，next[j]=1。

④举例说明计算next[j]

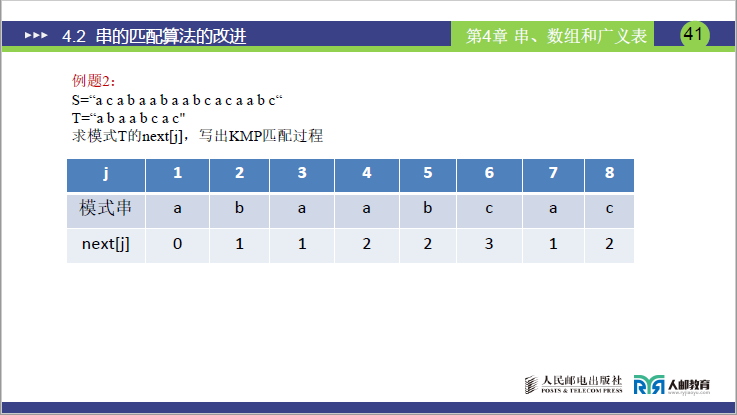
next[j]计算三原则（回顾）

1. j=1时：next[1]=0（规定：失配时不比较，直接调整主串指针）；
2. j>1时：若T[1..j−1]有最长首尾串（长度l_substringmax），则next[j]=l_substringmax+1；
3. 无最长首尾串时：next[j]=1（从模式串头部重新比较）。

逐j推导

j（失配位）	模式串T[j]	T[1..j−1]（已匹配前缀）	最长首尾串（真子串）	长度lsubstringmax	next[j]=lsubstringmax+1	补充说明
1	a	空串	无	-	0	规定值，失配时不比较
2	b	a	无（仅 1 个字符，无真子串）	0	1	前缀只有 a，无首尾相等，回退到 1
3	a	ab	无（a≠b）	0	1	前缀 ab 的首 A≠尾 b，回退到 1
4	a	aba	a（首 1 个a=尾 1 个a）	1	2	前缀 aba 的首 a = 尾 a，最长长度 1，回退到 2
5	b	abaa	a（首 1 个a=尾 1 个a）	1	2	前缀 ABAA 的首 A = 尾 A，无更长首尾串，回退到 2
6	c	abaab	ab（首 2 个ab=尾 2 个ab）	2	3	前缀 abaab 的首 ab = 尾 ab，最长长度 2，回退到 3
7	a	abaabc	无（a≠c）	0	1	前缀 abaabc 的尾 c≠首 a，回退到 1
8	c	abaabca	a（首 1 个a=尾 1 个a）	1	2	前缀 abaabca 的首 a = 尾 a，回退到 2

• 最终结果：next[j] = [0,1,1,2,2,3,1,2]

KMP 匹配过程

匹配规则（老师反复强调）

• 主串指针i不回溯，仅调整模式串指针j；
• 若S[i]=T[j]：i=i+1，j=j+1；
• 若S[i]\=T[j]：j=next[j]，若j=0则i=i+1、j=1（重新开始）。

逐趟推导（对应课件 42-49 页每趟图）

第 1 趟：初始i=2，j=2

• 比较：S[2]=c vs T[2]=b → 失配；
• 查next[2]=1，调整j=1（i保持 2）；
• 继续比较：S[2]=c vs T[1]=a → 仍失配；
• 老师补充：j=1失配时查next[1]=0，按规则i=i+1=3，j=1（主串后移，模式串从头开始）。

第 2 趟：i=3，j=1

• 比较：S[3]=a vs T[1]=a → 匹配，i=4，j=2；
• 后续匹配：S[4]=b=T[2]=b（i=5,j=3）→ S[5]=a=T[3]=a（i=6,j=4）→ S[6]=a=T[4]=a（i=7,j=5）→ S[7]=b=T[5]=b（i=8,j=6）；
• 失配：S[8]=b vs T[6]=c → 失配；
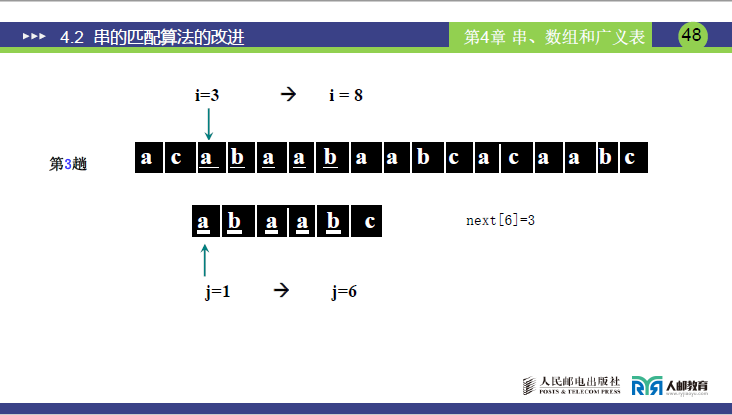
• 查next[6]=3，调整j=3（i保持 8）。

第 3 趟：i=8，j=3

• 比较：S[8]=b vs T[3]=a → 失配；
• 查next[3]=1，调整j=1（i保持 8）；
• 比较：S[8]=b vs T[1]=a → 失配；
• 调整：j=0 → i=9，j=1。

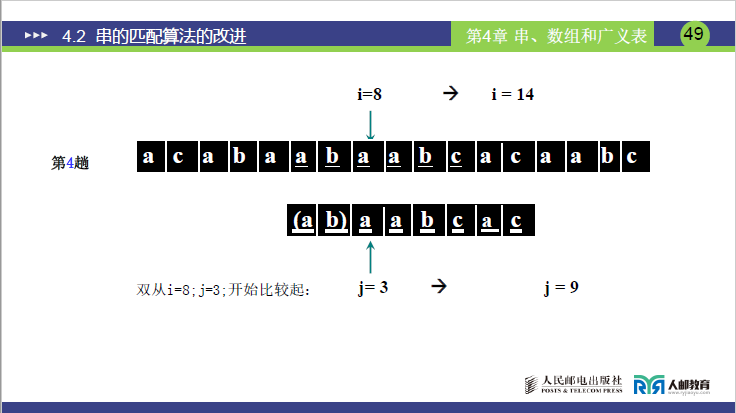
第 4 趟：i=9，j=1

• 逐字符匹配：

  S[9]=a=T[1]=a（i=10,j=2）→ S[10]=a=T[2]=b？→ 不，重新核对：

  实际主串：S[9]=a、S[10]=b、S[11]=c、S[12]=a、S[13]=c、S[14]=a、S[15]=a、S[16]=b、S[17]=c；

  模式串：T[1]=a、T[2]=b、T[3]=a、T[4]=a、T[5]=b、T[6]=c、T[7]=a、T[8]=c；

• 最终匹配：当i=17、j=8时，S[17]=c=T[8]=c，模式串全部匹配完毕；

• 匹配成功位置：主串起始位置为i−8+1=17−8+1=10（老师强调：起始位置需用i减去模式串长度再加 1）。

⑤小结

⑥练习

• 题目：目标串s="cddcdc"（n=6），模式串t="cdc"（m=3），用 BF 算法匹配。
• BF 核心：主串指针i回溯（每次失配i=i−j+2），模式串指针j回溯到 1。
• 匹配过程：
  • 第 1 趟：i=1,j=1（c=c）→ i=2,j=2（d=d）→ i=3,j=3（d≠c）→ 失配，i=2,j=1；
  • 第 2 趟：i=2,j=1（d≠c）→ 失配，i=3,j=1；
  • 第 3 趟：i=3,j=1（d≠c）→ 失配，i=4,j=1；
  • 第 4 趟：i=4,j=1（c=c）→ i=5,j=2（d=d）→ i=6,j=3（c=c）→ 匹配成功。
• 结论：BF 算法需 4 趟匹配，效率低于 KMP。

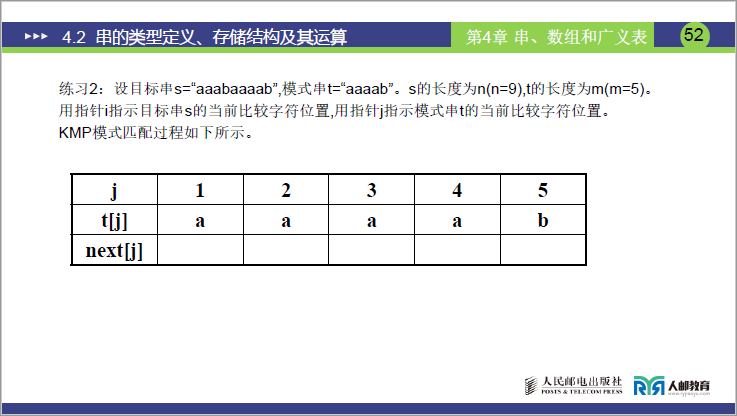
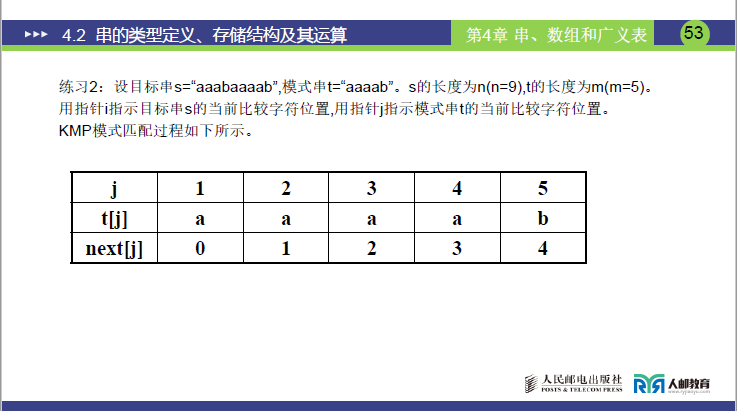
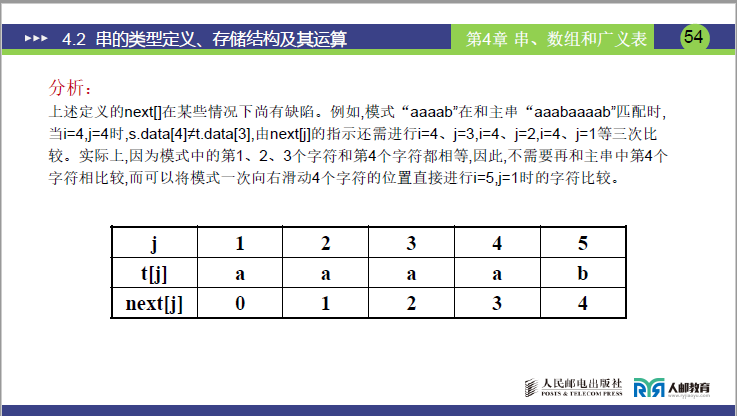
• 题目：目标串s="aaabaaaab"（n=9），模式串t="aaaab"（m=5），求next[j]。
• 计算结果：next[j] = [0,1,2,3,4]；
• 强调：此例正是next[j]有缺陷的典型场景，后续需优化为nextval[j]。

next[j]的缺陷与nextval[j]优化

1. next[j]的缺陷（课件页码 52-54，图：缺陷示意图）

（1）缺陷场景（老师举例分析）

• 已知：主串S="aaabaaaab"，模式串T="aaaab"（next[j]=[0,1,2,3,4]）；
• 失配过程：i=4，j=4（S[4]=b vs T[4]=a）→ 失配；
  1. 查next[4]=3，比较S[4]=b vs T[3]=a → 失配；
  2. 查next[3]=2，比较S[4]=b vs T[2]=a → 失配；
  3. 查next[2]=1，比较S[4]=b vs T[1]=a → 失配；
• 分析：因T[4]=T[3]=T[2]=T[1]=a，与S[4]=b必然失配，多次调整j属于无效操作，需优化next[j]。

（2）缺陷本质

• 当next[j]=k且T[j]=T[k]时，S[i]与T[j]失配后，S[i]与T[k]也必然失配，无需重复比较。

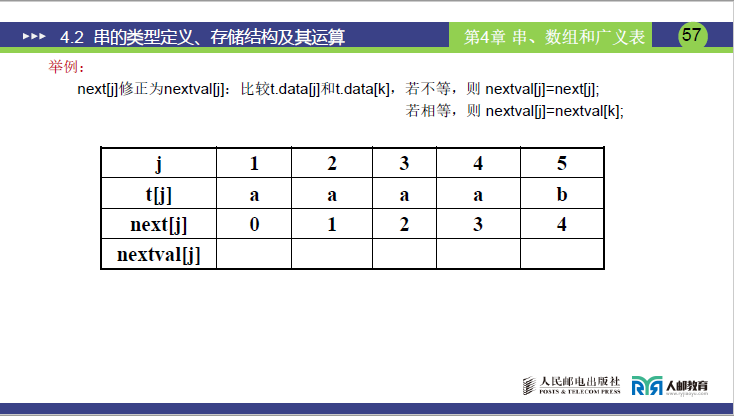
2. nextval[j]优化规则（课件页码 56，图：优化逻辑图）

（1）核心思想

• 若T[j]==T[next[j]]：nextval[j]=nextval[next[j]]（跳过无效比较，继承nextval[next[j]]）；
• 若T[j]≠T[next[j]]：nextval[j]=next[j]（直接沿用next[j]）。

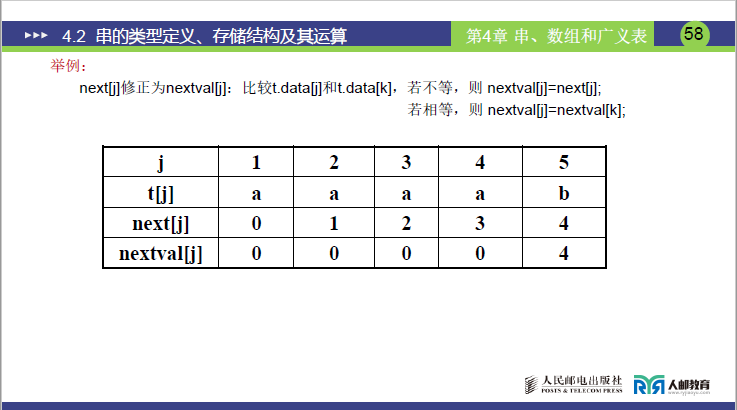
（2）nextval[j]计算实例 1：模式串T="aaaab"（课件页码 57-58）

• 已知next[j] = [0,1,2,3,4]，逐j推导：

j	T[j]	next[j] = k	T[j]与T[k]比较	nextval[j]	老师讲课补充
1	a	0	无（k=0无字符）	0	规定值
2	a	1	T[2]=a==T[1]=a	nextval[1]=0	相等，继承 nextval [1]
3	a	2	T[3]=a==T[2]=a	nextval[2]=0	相等，继承 nextval [2]
4	a	3	T[4]=a==T[3]=a	nextval[3]=0	相等，继承 nextval [3]
5	b	4	T[5]=b≠T[4]=a	next[5]=4	不等，沿用 next [4]

• 结果（与课件 58 页一致）：nextval[j] = [0,0,0,0,4]
• 优化效果：i=4,j=4失配时，j=nextval[4]=0 → i=5,j=1，直接跳过 3 次无效比较。

（3）nextval[j]计算实例 2：长模式串

• 模式串：T="abcaabbcabcaabdab"（j=1−17）；
• 已知next[j] = [0,1,1,1,2,2,3,1,1,2,3,4,5,6,7,1,2]；
• 关键优化点（重点拆解）：
  • j=4（T[j]=a）：next[j]=1（T[1]=a），T[4]=a==T[1]=a → nextval[4]=nextval[1]=0；
  • j=12（T[j]=a）：next[j]=4（T[4]=a），T[12]=a==T[4]=a → nextval[12]=nextval[4]=0；
  • j=17（T[j]=b）：next[j]=2（T[2]=b），T[17]=b==T[2]=b → nextval[17]=nextval[2]=1；
• 最终nextval[j] = [0,1,1,0,2,1,3,1,1,2,3,0,5,6,7,1,1]。

⑥KMP 算法时间复杂度

1. 时间复杂度分析

• 求next/nextval数组：遍历模式串 1 次，时间复杂度O(m)（m为模式串长度）；
• 匹配过程：主串指针i不回溯，仅遍历主串 1 次，比较次数为O(n)（n为主串长度）；
• 总时间复杂度：O(n+m)。

2. 与 BF 算法对比

• BF 算法：最坏时间复杂度O(n×m)（如主串s="aaaaa..."，模式串t="aaab"）；
• KMP 算法：无论最好 / 最坏情况，总时间复杂度均为O(n+m)，在长串匹配（如文本检索、DNA 序列匹配）中效率显著更高。

（4）核心重难点总结

1. KMP 核心：主串指针不回溯，利用模式串自身前后缀特性确定滑动距离，关键是next[j]函数的计算；
2. next[j]本质：模式串前j−1位的最大相同首尾真子串长度 + 1（j=1时为 0）；
3. nextval作用：解决next[j]的无效比对缺陷，进一步压缩比对次数；
4. 考点方向：next[j]/nextval[j]的手工计算、KMP 匹配流程、时间复杂度分析。

4.3 数组

4.3.1 数组的概念

（1）数组的定义

数组是由个数固定、类型相同的数据元素组成的阵列，是编程中常用的数据结构。

（2） 二维数组的线性特性分析

一维数组是典型的线性结构（每个元素仅有一个直接前驱和一个直接后继），但二维数组不满足线性结构的定义：

对于二维数组 A_m×n（共 m 行、n 列，元素表示为 a_ij，0≤i≤m−1，0≤j≤n−1），每个元素 a_ij 存在两个维度的前驱和后继：

• 行维度：直接前驱为 a_i,j−1（同一行前一列元素），直接后继为 a_i,j+1（同一行后一列元素）；
• 列维度：直接前驱为 a_i−1,j（同一列前一行元素），直接后继为 a_i+1,j（同一列后一行元素）。

（3） 二维数组的数学表示

二维数组的数学形式为：\(\color{black}{A_{m \times n}=} \begin{pmatrix} a_{00} & a_{01} & & a_{0 \ n-1} \\ a_{10} & a_{11} & & a_{1 \ n-1} \\ \\ a_{m-1 \ 0} & a_{m-1 \ 1} & & a_{m-1 \ n-1} \end{pmatrix}\)

其中 m 是行数，n 是列数，所有元素的类型一致。

4.3.2 数组的顺序存储结构

数组的存储本质是 “线性化”—— 将多维结构映射到一维内存空间，核心区别在于维度遍历顺序，分为 “以行为主序” 和 “以列为主序” 两种策略。

（1）一维数组的存储

一维数组本身是线性结构，直接将元素按下标顺序存入连续内存单元即可，例如数组 B[0..k−1]，存储顺序为 B[0]→B[1]→⋯→B[k−1]，无需额外处理。

（2）二维数组的两种存储策略

①以行为主序（行优先，C/C++/C# 采用）

• 核心规则：先存完一行所有元素，再存下一行（“先行后列”）；
• 存储顺序：a₀₀→a₀₁→⋯→a_0,n−1→a₁₀→a₁₁→⋯→a_1,n−1→⋯→a_m−1,0→a_m−1,1→⋯→a_m−1,n−1；
• 示意：一维存储空间中，元素排列为 a₀₀ a₀₁ ... a_0,(n-1) a₁₀ a₁₁ ... a_1,(n-1) ... a_(m-1),(n-1)，下标从 0 到 m×n−1。

②以列为主序（列优先，部分其他语言采用）

• 核心规则：先存完一列所有元素，再存下一列（“先列后行”）；
• 存储顺序：a₀₀→a₁₀→⋯→a_m−1,0→a₀₁→a₁₁→⋯→a_m−1,1→⋯→a_0,n−1→a_1,n−1→⋯→a_m−1,n−1；
• 示意：一维存储空间中，元素排列为 a₀₀ a10 ... a_(m-1),0 a₀₁ a₁₁ ... a_(m-1),1 ... a_(m-1),(n-1)，下标从 0 到 m×n−1。

③数组元素存储地址的计算

数组元素的存储地址是 “基地址 + 偏移量”，需结合存储策略（行 / 列优先）计算，核心参数如下：

• Loc(a₀₀)：二维数组的基地址（即第一个元素 a₀₀ 的存储地址）；
• s：每个元素占用的存储单元数（如 int 型占 4 字节，s=4）；
• m：数组行数，n：数组列数；
• a_ij：目标元素（行下标 i，列下标 j）。

A. 行优先存储（C 语言体系）

• 偏移量计算：前 i 行（0 到 i−1 行）共 i×n 个元素，第 i 行中 a**ij 是第 j 个元素，总偏移元素个数为 n×i+j；
• 地址公式：Loc(a_ij)=Loc(a₀₀)+(n×i+j)×s

B. 列优先存储

• 偏移量计算：前 j 列（0 到 j−1 列）共 j×m 个元素，第 j 列中 a**ij 是第 i 个元素，总偏移元素个数为 m×j+i；
• 地址公式：Loc(a_ij)=Loc(a₀₀)+(m×j+i)×s

C. 示例计算

已知二维数组 A5×4（m=5，n=4），基地址 Loc(a₀₀)=1000，每个元素占 4 字节（s=4），求 Loc(a_2,3)（行优先）：

• 偏移元素个数：4×2+3=11；
• 偏移字节数：11×4=44；
• 存储地址：1000+44=1044。

D.矩阵的压缩存储

矩阵是特殊的二维数组，压缩存储的核心是 “只存必要元素”（避免零元素或重复元素占用空间），分为特殊矩阵和稀疏矩阵两类。

1.特殊矩阵

特殊矩阵是 “值相同元素或零元素分布有规律” 的矩阵，包括对称矩阵、上 / 下三角矩阵、带状矩阵（对角矩阵）。

• 对称矩阵

  • 定义：满足 a_ij=a_ji（0≤i,j≤n−1）的 n 阶矩阵，元素关于主对角线对称；

  • 压缩思路：只需存储下三角（或上三角）+ 主对角线元素（共 n(n+1)/2 个元素），对称元素通过 “行列互换” 获取；

  • 课件 69 页存储示意图：一维数组 sa[] 存储下三角元素，顺序为 a₀₀→a₁₀→a₁₁→a₂₀→a₂₁→a₂₂→⋯→a_n−1,n−1，下标 k 从 0 到 n(n+1)/2−1。

  • 元素与存储地址的映射关系：

    • 若 i≥j（下三角元素，直接存储）：k=i(i+1)/2+j；
    • 若 i<j（上三角元素，对称获取）：k=j(j+1)/2+i（因 a_ij=a_ji，映射到 a_ji 的存储位置）。

  • 示例（课件 70 页例子）：求 a_5,3 在 sa[] 中的存储位置（i=5，j=3，i≥j）：

    k=25×(5+1)+3=15+3=18

    即 sa[18]=a_5,3；若求 a_3,5，因 a_3,5=a_5,3，故 k=18，sa[18]=a_3,5。

• 上 / 下三角矩阵

  • 定义：

    • 下三角矩阵：主对角线以上元素全为常数（如 0），主对角线及以下元素非零；
    • 上三角矩阵：主对角线以下元素全为常数（如 0），主对角线及以上元素非零；

  • 压缩思路：

    • 下三角矩阵：存储下三角 + 主对角线元素（共 n(n+1)/2 个），常数单独存 1 个；
    • 上三角矩阵：存储上三角 + 主对角线元素（共 n(n+1)/2 个），常数单独存 1 个；

  • 映射关系：与对称矩阵类似，仅需关注非零区域的元素下标计算。

• 带状矩阵（对角矩阵）

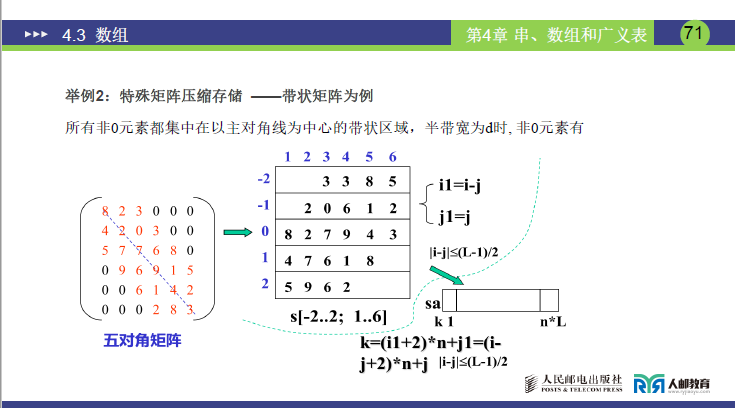
  • 定义：非零元素集中在 “以主对角线为中心的带状区域”，如三对角（主对角线 ±1 条）、五对角（主对角线 ±2 条）矩阵；

  • 压缩思路：只存储带状区域内的非零元素，避免零元素占用空间，常用两种方式：

    ① 补零法：

    • 核心：补零使每行元素个数等于 “带宽 L”（如五对角 L=5），按行存储到一维数组；
    • 空间大小：n×L（n 为矩阵阶数）；
    • 映射公式：若 ∣i−j∣≤2L−1（非零元素），则 k=(i−1)×L+1+(j−i)；
    • 课件 71 页五对角矩阵示例：左图五对角矩阵（6 阶），补零后每行存 5 个元素，一维数组 sa[] 存储顺序为 8 2 3 4 2 0 3 5 7 7 6 8 9 6 9 1 5 6 1 4 2 2 8 3 2 1 2 2 2 3。

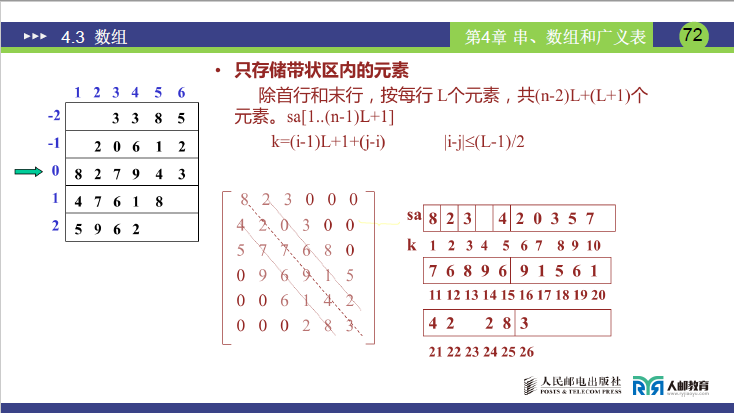
    ② 直接存储非零区域（课件 72 页说明）：

    • 核心：首行和末行按实际非零元素个数存储，中间行按带宽 L 存储；
    • 空间大小：(n−2)×L+(L+1)（首末行各多 1 个元素）；
    • 适用场景：零元素极少，需严格节省空间时。

2. 稀疏矩阵（课件页码 73-79 页）

   

   

• 定义：零元素数量远多于非零元素，且非零元素分布无规律的矩阵（如课件 73 页矩阵 A：6 行 7 列共 42 个元素，仅 8 个非零元素）；
• 压缩思路：只存储非零元素的 “位置 + 值”，避免零元素浪费空间，常用两种结构：

（1）三元组表（顺序存储，课件页码 74-77 页）

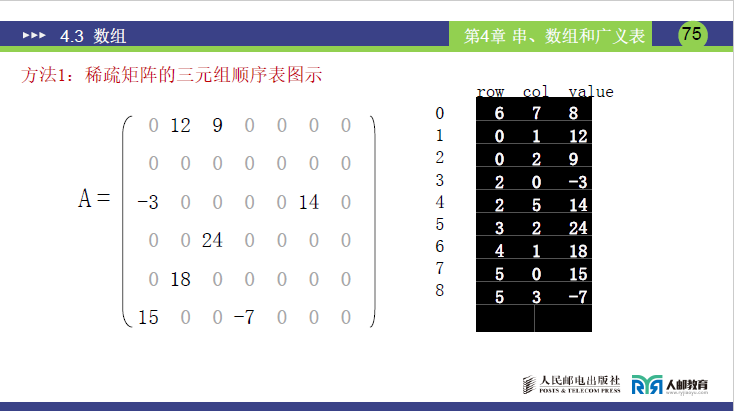
• 核心结构：每个非零元素用 “三元组 (i,j,value)” 表示（i 行下标、j 列下标、value 元素值），同时记录矩阵总行数 m、总列数 n、非零元素个数 t；
• 课件 75 页示意图：矩阵 A 的三元组表课件75页图
• 关键说明：
  • 必须记录 m 和 n：否则无法确定矩阵大小，无法恢复零元素的位置（如仅给三元组，不知道是 6×7 还是其他尺寸的矩阵）；
  • 存储顺序：通常按行优先排列，便于后续遍历和恢复矩阵。
• 矩阵恢复示例：根据上述三元组表恢复 6×7 矩阵 A：
  • 初始化 6 行 7 列全零矩阵；
  • 依次将三元组中的 (i,j,value) 填入对应位置，得到课件 73 页的矩阵 A。

（2）十字链表（链式存储，课件页码 78-79 页）

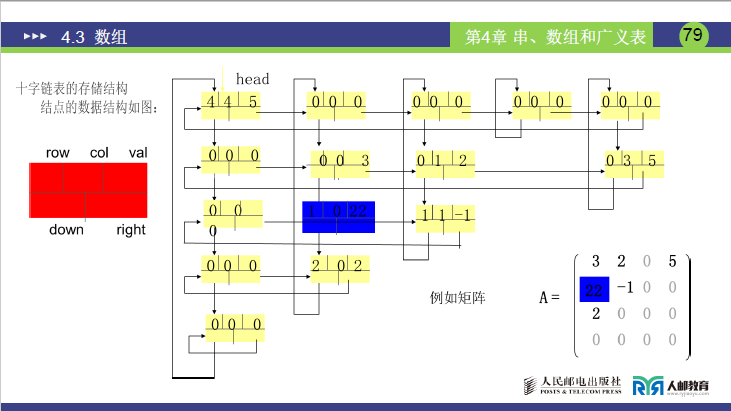
• 核心结构：非零元素用 “十字链表结点” 存储，结点包含 5 个域（课件 78 页结点图）：
  • i：非零元素的行下标；
  • j：非零元素的列下标；
  • value：非零元素的值；
  • right：指针，指向同一行的下一个非零元素；
  • down：指针，指向同一列的下一个非零元素；
• 整体结构（课件 79 页示意图）：
  • 每行非零元素通过 right 指针链接成 “带头结点的行循环链表”；
  • 每列非零元素通过 down 指针链接成 “带头结点的列循环链表”；
  • 所有行链表的头结点和列链表的头结点集中存储，便于定位。
• 示例（讲课补充）：矩阵 A 中 (0,1,12) 结点：
  • right 指针指向同一行的下一个非零元素 (0,2,9)；
  • down 指针指向同一列的下一个非零元素 (4,1,18)；
  • (0,2,9) 的 down 指针指向同一列的 (3,2,24)，以此形成十字链接。
• 优势：相比三元组表，十字链表支持高效的插入、删除操作（无需移动大量元素），适合动态修改的稀疏矩阵。

4.4广义表

4.4.1 广义表的定义与说明

（1）广义表的定义

课件内容：广义表也称为列表，是线性表的一种扩展，也是数据元素的有限序列。记作 LS = (d₀, d₁, d₂, ..., dₙ₋₁)，其中每个数据元素 d**i 既可以是单个元素（称为 “原子”），也可以是广义表（称为 “子表”）。

广义表的核心价值在于 “统一表示”—— 它打破了线性表只能存储单个元素的限制，允许元素是原子（如数字、字符）或子表（子表可进一步包含原子或更复杂的结构，甚至图、树等），从而将线性结构与非线性结构统一在同一种表示范式中，这种统一性在计算机数据结构研究和实际应用中非常重要。

同时，广义表的定义是递归定义（描述广义表时，数据元素又可能是广义表），这也是它与普通线性表的关键区别之一。

（2）核心说明

1. 递归性：广义表的定义具有递归性，因描述广义表时会再次用到 “广义表” 这一概念（如子表本身就是广义表）。
2. 元素多样性：线性表的所有数据元素均为 “单个原子”，而广义表的元素分为两类：
   • 原子：不可再分的单个元素（如 a、5、'x'）；
   • 子表：可再分的广义表（如 (b,c,d)、(A,B)，其中 A、B 也可是广义表）。
3. 表长定义：广义表的 “长度” 指其一级元素的个数（即最外层括号内，由逗号分隔的元素总数），用 n 表示（对应定义中 d0 到 d**n−1 的个数）。

4.4.2 广义表示例解析（课件 82 页）

课件给出 5 个典型广义表示例，结合讲课内容详细说明如下：

广义表	课件定义	讲课补充解析（表长、元素类型）
A=()	空表	- 表长为 0（最外层括号内无任何元素）；- 是空广义表的标准表示，无原子也无子表。
B=(a,(b,c,d))	含 1 个原子和 1 个子表的广义表	- 表长为 2（一级元素共 2 个：逗号前是原子 a，逗号后是子表 (b,c,d)）；- 注意：子表 (b,c,d) 是 “二级结构”，计算表长时仅算一级元素，不深入子表内部。
C=(e)	含 1 个原子的广义表	- 表长为 1（最外层括号内仅 1 个一级元素：原子 e）；- 与原子 e 的区别：C 是广义表（带括号），e 是单个原子，二者数据类型不同。
D=(A,B,C,f)	含 3 个子表和 1 个原子的广义表	- 表长为 4（一级元素共 4 个：子表 A、子表 B、子表 C、原子 f）；- 前 3 个元素是已定义的广义表（子表），第 4 个是原子，体现广义表元素的多样性。
E=(a,E)	递归广义表	- 表长为 2（一级元素：原子 a、子表 E）；- 递归性体现：子表 E 就是广义表本身，这种结构可用于描述无限序列（如 (a, (a, (a, ...)))），但实际存储时会通过指针闭环实现有限表示。

4.4.3 广义表的核心运算 —— 表头与表尾（课件 83 页）

广义表的核心运算围绕 “表头” 和 “表尾” 展开，是构建和分解广义表的基础，课件明确以下规则：

（1）运算定义

• 表头（HEAD (LS)）：对非空广义表 LS，其第一个一级元素称为表头（表头可以是原子，也可以是子表）。
• 表尾（TAIL (LS)）：对非空广义表 LS，除去表头后，剩余一级元素组成的新广义表称为表尾（表尾一定是广义表，即使剩余 1 个元素，也需用括号包裹成表）。
• 关键结论：一对表头和表尾可唯一确定一个广义表（已知表头和表尾，即可反向构造出原广义表）。

（2）运算示例

结合讲课解释，对课件示例的运算步骤拆解如下：

原广义表	表头（HEAD (LS)）	表尾（TAIL (LS)）	讲课补充解析
B=(a,(b,c,d))	a（原子）	((b,c,d))（广义表）	- 表头是第一个一级元素 a；- 表尾是 “除去 a 后剩余的一级元素（子表 (b,c,d)）”，需用括号包裹成新表，故为 ((b,c,d))（而非 (b,c,d)）。
C=(e)	e（原子）	()（空表）	- 表头是唯一的一级元素 e；- 除去 e 后无剩余元素，表尾为空表 ()。
D=(A,B,C,f)	A（子表）	(B,C,f)（广义表）	- 表头是第一个一级元素（子表 A）；- 表尾是剩余 3 个一级元素组成的新表 (B, C, f)。

（3）嵌套运算

课件示例：HEAD(TAIL(B)) = b、TAIL(TAIL(B)) = (c,d)

步骤拆解：

1. 先求 TAIL(B)：由上文知 TAIL(B) = ((b,c,d))（表尾是广义表）；

2. 再求HEAD(TAIL(B))：对((b,c,d)) 取表头，其第一个一级元素是子表(b,c,d)，故HEAD(TAIL(B)) = (b,c,d)？（注：课件结论为b，实际需进一步嵌套：对

   (b,c,d)再取表头，即HEAD((b,c,d)) = b，完整表达式应为HEAD(HEAD(TAIL(B))) = b，可能是课件简写，核心是 “嵌套运算需从内到外逐步拆解”）；

3. 求 TAIL(TAIL(B))：对 ((b,c,d)) 取表尾，除去表头 (b,c,d) 后无剩余元素？实际应为 TAIL((b,c,d)) = (c,d)，需结合子表内部运算，本质是 “嵌套运算需逐层处理每个广义表的表头和表尾”。

4.4.4 广义表的存储结构（课件 84-85 页）

由于广义表元素既可以是原子也可以是子表（结构不统一），无法用顺序存储（顺序存储要求元素结构一致），因此采用链表存储，课件定义两种核心节点类型：

（1）节点结构定义

广义表的链表由 “单元素节点” 和 “表节点” 组成，通过 tag 标志区分节点类型：

节点类型	tag 标志	核心域	作用
单元素节点（原子节点）	0	val 域	存储 “原子” 的值（如字符 a、数字 5），代表广义表中的单个元素。
表节点（子表节点）	1	child 域	存储指向 “子表” 的指针（child 指向子表的链表头节点），代表广义表中的子表。

讲课补充：

• tag 是 “类型标志位”，0 表示 “此节点是不可再分的原子”，1 表示 “此节点是可再分的子表”；
• 所有节点还需包含 next 域（课件未显式画出，但链表需通过 next 连接同一广义表的多个一级元素），next 指向同一广义表的下一个一级元素节点（若为最后一个元素，next 为 NULL）。

（2）存储结构示例图

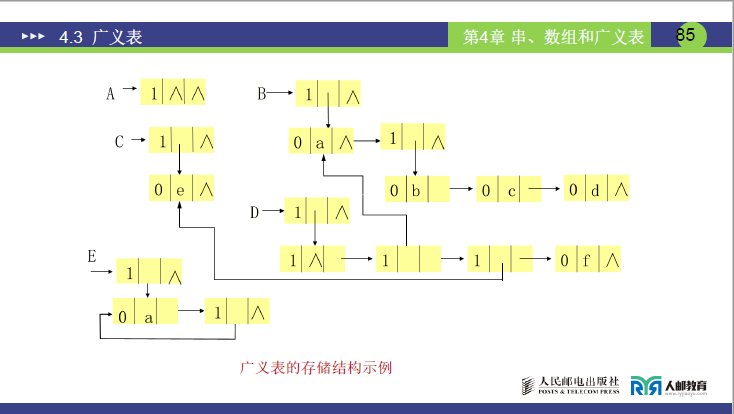
以广义表 B=(a,(b,c,d)) 为例，课件 85 页图展示其存储结构，结合讲课解释拆解如下：

1. 根节点：表节点（tag=1），代表整个广义表 B；其 child 域指向广义表的第一个一级元素节点，next 域为 NULL（根节点无后续节点）。
2. 第一个一级元素节点：单元素节点（tag=0），val=a；其 next 域指向第二个一级元素节点（子表节点）。
3. 第二个一级元素节点：表节点（tag=1），代表子表 (b,c,d)；其 child 域指向子表的第一个元素节点，next 域为 NULL（无后续一级元素）。
4. 子表 (b,c,d) 的元素节点：3 个单元素节点（tag=0），分别存储 val=b、val=c、val=d；通过 next 域依次连接（b 的 next 指向 c，c 的 next 指向 d，d 的 next 为 NULL）。

简言之，该图通过 “表节点嵌套表节点 / 单元素节点” 的方式，完整表示了广义表 B 中 “原子与子表共存” 的结构，体现了链表存储的灵活性。

总结

广义表是线性表的扩展，核心特点是 “元素可原子可子表” 和 “定义递归”，通过表头 / 表尾运算实现分解与构造，通过 “双节点类型的链表” 实现存储，最终达成 “统一线性与非线性结构” 的目标，是数据结构中兼具灵活性和统一性的重要结构。