第3章栈和队列

第3章栈和队列

1. 知识体系中的位置

   • 属于常用线性结构，承接第二章 “线性表”，后续第五章、第六章为非线性结构（树、图）。

2. 栈与队列的关联

   • 二者均为常用线性结构，采用对应式学习方法：栈的核心规则是 “后进先出”，队列是 “先进先出”。

3. 数据结构通用学习要点

   学习任意数据结构，均围绕 4 个核心要点展开：

   定义与特点、描述、操作、存储

   （栈和队列的学习也遵循此逻辑）。

3.1 栈的定义和特点

3.1.1 栈的定义

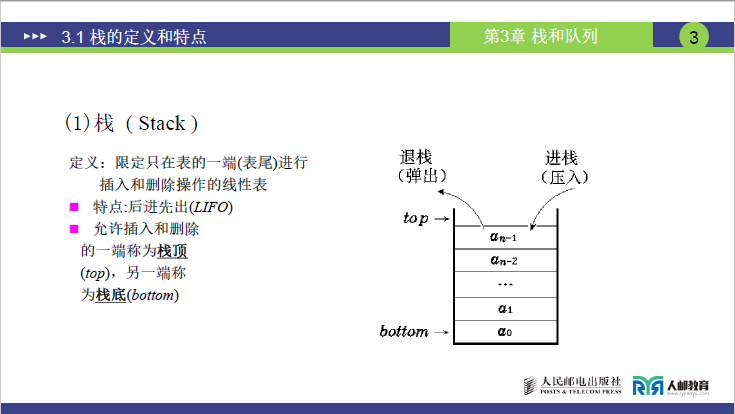
• 定义：限定只在表的一端（表尾）进行插入和删除操作的线性表。

• 补充解释：

  ① 栈是 “特殊的线性表”：栈属于线性表，但线性表≠栈（普通线性表可在任意位置插入 / 删除，栈仅限制一端操作）。

  ② 栈的实际使用（C/C++ 前导课程）：大量用栈能提升程序可读性，但因频繁执行 “入栈 / 出栈”，运行效率相对较低。

3.1.2 栈的核心术语（对应课件 3.1 中的栈结构示意图）

• 栈顶（top）：

  允许执行 插入（进栈 / 压入）、删除（退栈 / 弹出） 操作的一端（是栈的 “活动端”）。

• 栈底（bottom，注：讲课中 “button” 为识别错误）：

  不允许执行插入、删除操作的一端（是栈的 “固定端”）。

3.1.3 栈的特点：后进先出（LIFO，Last In First Out）

• 逻辑推导（结合课件 3.1 中的栈结构示意图）：

  若元素按a₀ → a₁ → … → aₙ₋₁的顺序依次 “进栈”（从栈顶插入），由于仅能操作栈顶，出栈时需先取出最后进入的aₙ₋₁，再依次取出aₙ₋₂… 最后取出最早进入的

  a₀。

• 结论：后进入栈的元素先出栈，先进入栈的元素后出栈，即 “后进先出”，也可表述为 “先进后出”。

3.2 栈的表示和操作的实现

栈的存储结构从理论上可分为顺序存储、链式存储、索引存储、散列存储四种，但本课程前六章重点研究前两种，因此本节主要讲解顺序栈（栈的顺序存储结构） 和链栈（栈的链式存储结构） 。

3.2.1 顺序栈 —— 栈的顺序存储结构

（1）定义

定义：限定在表尾进行插入和删除操作的顺序表（仅允许在 “表尾” 这一端操作，其他端不可操作）。

补充：顺序栈的核心是通过 “栈底指针（bottom）” 和 “栈顶指针（top）” 管理元素，其中bottom始终指向栈底（固定不变，初始化后不再移动），top动态指向栈顶元素的下一个空存储单元（关键指针，控制进栈 / 退栈）。

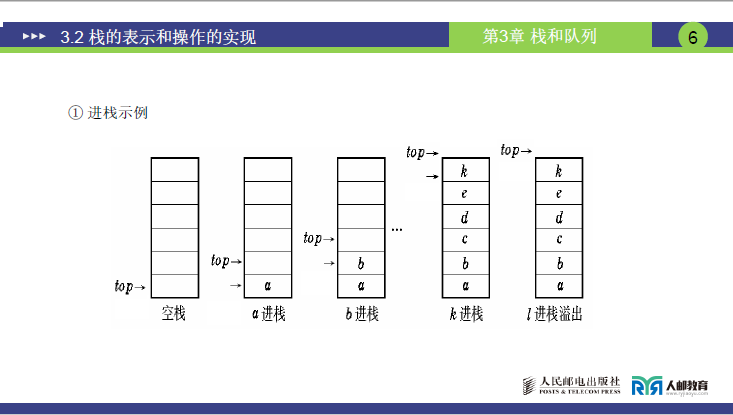
① 进栈示例

进栈核心规则：先进后动指针（先存元素，再移 top）

1. 初始状态（空栈）：top指向顺序表的第一个空存储单元，bottom指向栈底（与空栈时的top位置一致，后续固定），栈内无元素。
2. a 进栈：先将元素a存入top当前指向的存储单元，再将top向上移动 1 位（指向新的空单元）。
3. b 进栈：重复上述操作 —— 先存b到当前top位置，再移top。
4. k 进栈：同理，存k后top继续上移，此时栈内元素为a、b、...、k，top指向k的下一个空单元。
5. l 进栈（溢出）：若栈的最大容量已被占满（top超出栈的存储范围），此时无法再存入l，称为上溢（overflow）。

补充：生活中的栈示例 —— 军训时枪膛压子弹，最后压入的子弹（对应栈顶元素）会最先被打出，完全符合 “后进先出（LIFO）” 特性；进栈前必须判断 “栈是否已满”，避免上溢。

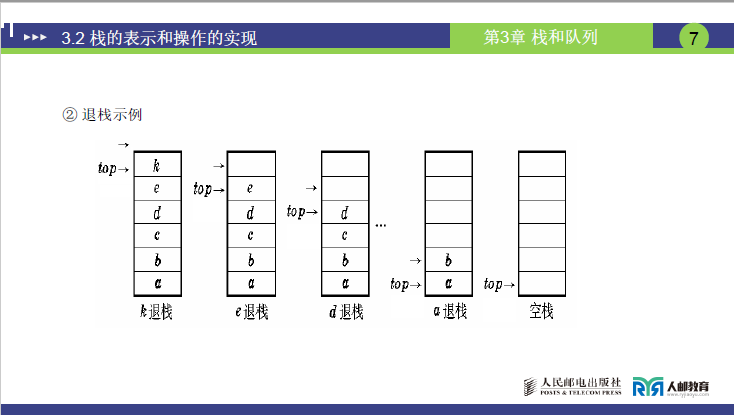
② 退栈示例

退栈核心规则：先动指针再退（先移 top，再取元素）

1. 初始状态（栈满，含 k、e、d、...、a）：top指向k的下一个空单元。
2. k 退栈：先将top向下移动 1 位（指向k所在的存储单元），再取出k；此时栈内元素为a、b、...、e。
3. e 退栈：重复上述操作 —— 先移top指向e，再取e。
4. d 退栈、a 退栈：同理，直到a退栈后，top回到空栈时的初始位置（与bottom重合）。
5. 继续退栈（溢出）：若top已与bottom重合（空栈），仍尝试退栈，称为下溢（underflow）。

讲课补充：

• 退栈前必须判断 “栈是否为空”，避免下溢；
• 内存操作特性：仅 “写操作”（进栈、退栈）会改变栈内数据和top位置；“读操作”（如取栈顶元素）仅读取数据，不移动top，也不破坏栈内元素。

③几点说明

1. 上溢：栈满时仍执行进栈操作，属于 “致命错误”（需扩容或避免）；
2. 下溢：栈空时仍执行退栈操作，属于 “逻辑错误”（需提前判断栈空）；
3. top的指向规律：初始化时top指向顺序表第一个空单元，始终指向 “栈顶元素的下一个空存储单元”，而非栈顶元素本身 —— 这是 “先进后动、先动后退” 规则的核心依据。

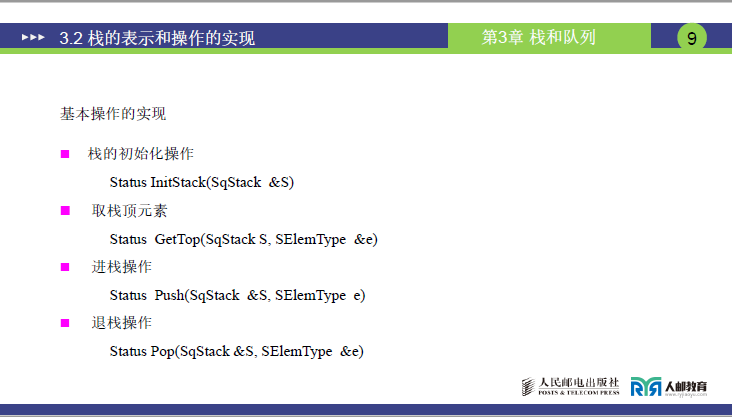
④基本操作的实现

顺序栈的核心操作共 4 种，均需通过代码实现（后续 “巩固提升篇” 编程练习），具体功能如下：

操作名称	函数原型	功能说明	讲课补充（操作细节）
栈的初始化	Status InitStack(SqStack &S)	将栈S置为空栈，初始化bottom和top的初始位置	top与bottom指向同一初始位置，栈内无元素
取栈顶元素	Status GetTop(SqStack S, SElemType &e)	读取栈顶元素，存入e中	读操作，top不移动，仅复制栈顶元素（S.data[top-1]）
进栈操作	Status Push(SqStack &S, SElemType e)	将元素e压入栈S的栈顶	写操作，先存e到S.data[top]，再top++
退栈操作	Status Pop(SqStack &S, SElemType &e)	将栈S的栈顶元素弹出，存入e中	写操作，先top--，再取S.data[top]存入e

注：Status为状态类型（如成功返回OK，失败返回ERROR），SqStack为顺序栈结构体类型，SElemType为栈元素的数据类型（如int、char）。

3.2.2 链栈 —— 栈的链式存储结构

（1）定义

定义：不带头结点的单链表，其插入和删除操作仅限制在表头位置进行，链表的头指针即栈顶指针（top）。

• 链栈的节点结构包含两部分：data域（存储元素值）和next域（指向后一个节点的指针）；
• 无需bottom指针：通过节点的next域串联栈底（最后一个节点的next为NULL），栈底位置由链表结构自然确定。

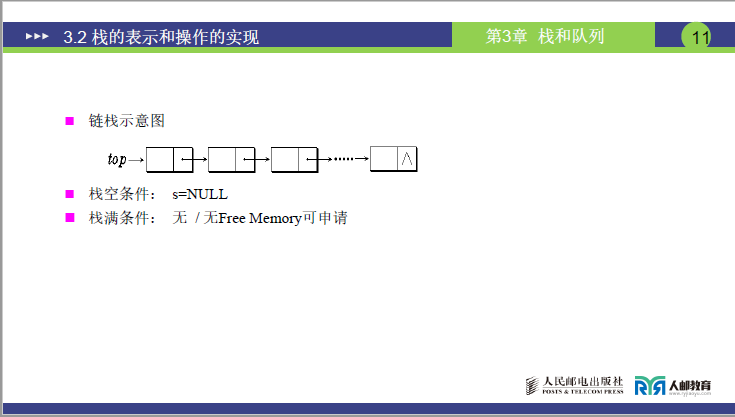
（2）链栈示意图

• 栈顶指针top指向链表的表头节点（栈顶元素）；
• 每个节点的next指针指向 “下一个元素”（栈内的前一个元素）；
• 栈底节点的next为NULL（无后续节点）；
• 空栈条件：top = NULL（链表无节点，无元素可操作）；
• 栈满条件：无固定满条件 —— 仅当内存无空闲空间（Free Memory）时，无法申请新节点，视为栈满；若支持动态内存申请，链栈可无限扩容（无实际栈满）。

（3）链栈的操作特点

1. 进栈：在链表表头插入新节点 —— 新节点的next指向原栈顶节点（top），再将top指向新节点（新节点成为新栈顶）；
2. 退栈：在链表表头删除节点 —— 先保存原栈顶节点的data和next，再将top指向原栈顶的next，最后释放原栈顶节点；
3. 优缺点分析：
   • 优点：无需提前确定栈容量，可动态扩容；
   • 缺点：每个节点需额外存储next指针（浪费空间），且栈仅在表头操作（顺序栈已能高效实现，链式存储无效率优势）；
   • 结论：无特殊需求时，优先使用顺序栈（更高效、节省空间）。

3.2.3 栈的应用

栈的核心特性是 “后进先出（LIFO）”，可解决需 “倒序处理” 或 “优先级处理” 的问题，本节重点讲解两种典型应用：数制转换、表达式求值。

① 数制转换

应用场景

将十进制数N转换为d进制数（如d=2二进制、d=8八进制、d=16十六进制），核心原理基于 “除d取余，倒排余数”。

转换原理（课件公式）

N=(n div d)×d+(n mod d)

• div：整除运算（取商，向下取整）；
• mod：求余运算（取余数，范围0~d-1）；
• 步骤：反复用d除N，记录每次的余数，直到商为0；最后将余数 “倒序排列”，即为d进制结果（余数的产生顺序与最终结果顺序相反，需用栈实现倒序）。

课件示例：(1348)₁₀ = (2504)₈

详细计算过程（结合栈的操作）：

计算步骤	被除数n	整除n div 8（商）	求余n mod 8（余数）	栈操作（余数进栈）
1	1348	168	4	4 进栈（栈：[4]）
2	168	21	0	0 进栈（栈：[4,0]）
3	21	2	5	5 进栈（栈：[4,0,5]）
4	2	0	2	2 进栈（栈：[4,0,5,2]）
结束	商为 0	-	-	余数出栈（2→5→0→4）

最终结果：出栈顺序为2、5、0、4，即 (1348)₁₀ = (2504)₈。

讲课补充示例：(75)₁₀ = (1001011)₂

详细计算过程：

计算步骤	被除数n	整除n div 2（商）	求余n mod 2（余数）	栈操作（余数进栈）
1	75	37	1	1 进栈（栈：[1]）
2	37	18	1	1 进栈（栈：[1,1]）
3	18	9	0	0 进栈（栈：[1,1,0]）
4	9	4	1	1 进栈（栈：[1,1,0,1]）
5	4	2	0	0 进栈（栈：[1,1,0,1,0]）
6	2	1	0	0 进栈（栈：[1,1,0,1,0,0]）
7	1	0	1	1 进栈（栈：[1,1,0,1,0,0,1]）
结束	商为 0	-	-	余数出栈（1→0→0→1→0→1→1）

最终结果：出栈顺序为1、0、0、1、0、1、1，即 (75)₁₀ = (1001011)₂。

② 表达式求值

应用场景

计算中缀表达式（运算符在操作数中间，如3*(7-2)）的值 —— 计算机无法直接识别中缀表达式的优先级（如先算括号内、再算乘除、后算加减），需用 “双栈” 实现优先级管理。

核心概念

1. 双栈结构：
   • OPND栈（操作数栈）：存储操作数或中间计算结果；
   • OPTR栈（运算符栈）：存储运算符（含括号()、结束符#），管理运算符优先级；
2. 算符优先级规则（课件 + 讲课补充）：
   • 常规优先级：乘除（*、/）> 加减（+、-）；
   • 括号优先级：左括号( > 括号外运算符，左括号( < 括号内运算符；右括号) < 括号内运算符；
   • 结束符#：优先级最低，用于标记表达式的开始和结束（表达式首尾需加#，如#3*(7-2)#）；
   • 特殊规则：)遇到(时，两者一起从OPTR栈弹出（无数据计算）；#遇到#时，表达式计算结束。

算法思想

1. 初始化：OPND栈置空；OPTR栈压入#（栈底，标记开始）；
2. 扫描表达式：从左到右依次读取每个字符（记为c）：
   • 若c是操作数：直接压入OPND栈；
   • 若c是运算符：与OPTR栈顶运算符（记为top_op）比较优先级：
     • 若c优先级 > top_op：c压入OPTR栈；
     • 若c优先级 < top_op：OPTR栈弹出top_op，OPND栈弹出两个操作数（先弹b，后弹a），计算a top_op b，结果压入OPND栈；
     • 若c是)且top_op是(：OPTR栈弹出(和)（仅弹运算符，不弹操作数）；
     • 若c是#且top_op是#：OPTR栈弹出#，计算结束（OPND栈剩余元素即为结果）；
3. 结束：OPND栈的唯一元素即为表达式的值。

课件示例：计算3*(7-2)【页码 16】

步骤 1：表达式补#，变为#3*(7-2)#；初始化OPND=[]，OPTR=[#]。

步骤 2：逐字符扫描计算：

最终结果：表达式3*(7-2)的值为15。

扫描字符	数据栈（存操作数）	运算符栈（存运算符）	操作逻辑
#	[]	[#]	运算符栈空，压入 “#”。
3	[3]	[#]	数据直接压入数据栈。
*	[3]	[#, *]	“*” 优先级 > 栈顶 “#”，压入运算符栈。
(	[3]	[#, *, (]	“(” 优先级> 栈顶 “*”，压入运算符栈。
7	[3, 7]	[#, *, (]	数据直接压入数据栈。
-	[3, 7]	[#, *, (, -]	“-” 优先级 > 栈顶 “(”，压入运算符栈。
2	[3, 7, 2]	[#, *, (, -]	数据直接压入数据栈。
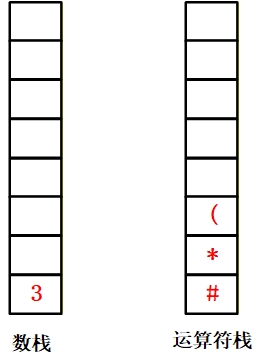
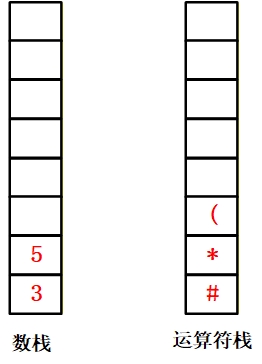
)	[3, 5]	[#, *]	1. “)” 优先级 < 栈顶 “-”，弹出 “-”；2. 数据栈弹 2（第二个操作数）、弹 7（第一个操作数），算 7-2=5，压回数据栈；3. 运算符栈顶为 “(”，与 “)” 配对，同时弹出。
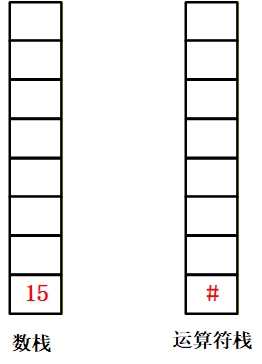
#	[15]	[]	1. “#” 优先级 < 栈顶 “”，弹出 “”；2. 数据栈弹 5（第二个操作数）、弹 3（第一个操作数），算 3×5=15，压回数据栈；3. 两 “#” 相遇，计算结束，弹出所有栈元素。
✅ 最终结果：数据栈剩余 15，即3*(7-2)=15。

1.初始化双栈：数据栈为空，运算符栈先压入左侧 “#”；

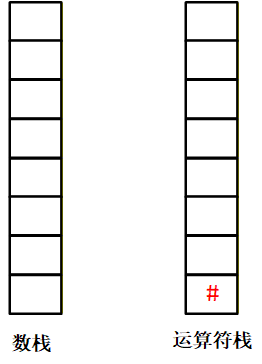
2.从左到右扫描表达式：
遇到 “3”（数据）：直接压入数据栈；

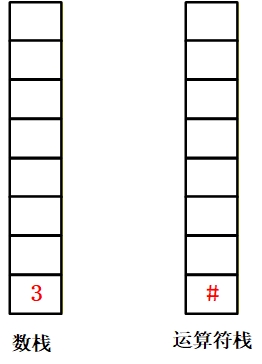
3.遇到 “*”（运算符）：优先级高于栈顶 “#”，压入运算符栈；

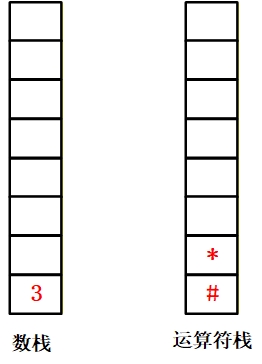
4.遇到 “(”（左括号）：优先级高于栈顶 “*”，压入运算符栈；

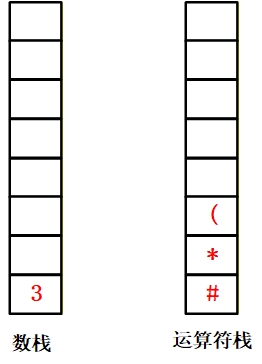
5.遇到 “7”（数据）：压入数据栈；

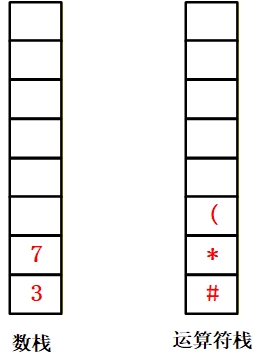
6.遇到 “-”（运算符）：优先级高于栈顶 “(”，压入运算符栈；

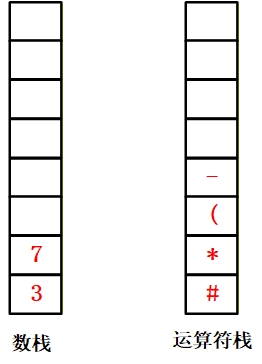
7.遇到 “2”（数据）：压入数据栈；

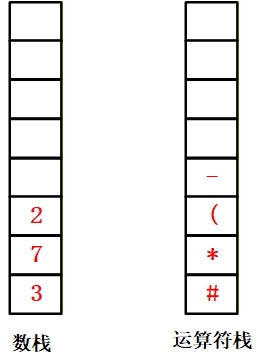
8.遇到 “)”（右括号）：优先级低于栈顶 “-”，需先弹出 “-”；此时从数据栈弹出两个元素（先弹 2，后弹 7），计算 7-2=5，将 5 压回数据栈；接着运算符栈顶为 “(”，与 “)” 配对，两者同时弹出（数据栈不操作）；

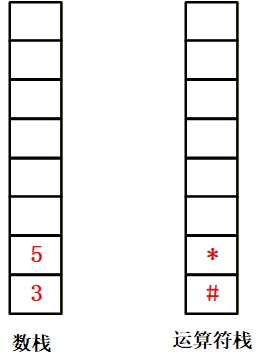
9.遇到 “#”（右侧）：优先级低于栈顶 “”，弹出 “”；从数据栈弹出两个元素（先弹 5，后弹 3），计算 3*5=15，将 15 压回数据栈；最后两个 “#” 相遇，表达式计算结束，弹出所有栈元素，数据栈中剩余的 15 就是结果。

3.2.4 栈的小结

1. 栈的存储：
   • 顺序栈：基于数组，bottom固定，top动态移动，优先使用（高效、省空间）；
   • 链栈：基于不带头结点的单链表，top为头指针，适合动态扩容场景；
2. 栈的操作：
   • 核心操作：初始化、取栈顶（读）、进栈（写，先进后动）、退栈（写，先动后退）；
   • 关键判断：进栈前判栈满（防上溢），退栈前判栈空（防下溢）；
3. 栈的应用：
   • 数制转换：利用栈 “倒排余数”；
   • 表达式求值：利用双栈管理 “操作数” 和 “运算符优先级”。

3.3 队列的定义和特点

3.3.1 队列的定义与核心特点

（1）队列的定义

• 定义：限定在表的一端进行删除，在表的另一端进行插入操作的线性表。允许删除的一端叫做队头（front），允许插入的一端叫做队尾（rear）。
• 与栈的核心区别：栈仅允许在同一端执行插入（进栈）和删除（退栈）操作，另一端完全固定；而队列是 “两端分工”—— 队尾仅负责插入（入队），队头仅负责删除（出队），每端功能唯一，不可混淆。
• 生活场景类比：队列对应现实中的 “排队”（如买票、上公交、食堂打饭），核心规则是 “禁止插队”（不允许在队列中间插入元素），必须从队尾排队（入队）、从队头离开（出队），符合现实中 “守规矩” 的操作逻辑。

（2）队列的核心特性：先进先出（FIFO，First In First Out）

• 特性：FIFO（First In First Out），图示（出队列 a₀ ..... aₙ₋₁，入队列，队头 队尾）。
• 逻辑本质：最早进入队列的元素（先入队），会最早离开队列（先出队），与生活中 “先来先服务” 的规则完全一致。例如：先到公交站的人先上车，先到食堂的人先打饭。
• 反例对比：若用栈的 “先进后出” 规则处理排队（比如 “排站”），会出现 “后来的人先上车、先买票”，完全违背现实逻辑，因此生活中只说 “排队（队列）”，不说 “排站（栈）”。
• 图示结构：队列整体标注为 “Q”，元素序列从 a₀ 到aₙ₋₁；左端明确标注 “队头”，对应 “出队列” 操作（删除元素的唯一端口）；右端明确标注 “队尾”，对应 “入队列” 操作（插入元素的唯一端口）。
• 图示意义：直观体现 “一端入、一端出” 的限制，且 a₀（最早入队的元素）位于队头位置，会最早出队，直接可视化了 FIFO 特性。

3.3.2 队列的基本操作

（1）基本操作列表

• 队列基本操作：初始化、求队列的长度、入队、出队、判队空、判队满、取队头元素。

• 操作数量与栈的差异：队列的基本操作共 7 个，相比栈的 4 个核心操作（初始化、进栈、退栈、取栈顶），新增了 “求队列长度” 和 “判队满”—— 这是由队列 “两端操作” 的特性决定的：需通过 “判队满” 避免入队时溢出，需通过 “求长度” 统计当前队列元素数量（如现实中 “统计排队人数”）。

• 各操作的现实场景映射：

  • 初始化：创建一个空队列（如 “打开超市收银台的排队通道，准备开始服务”）；
  • 求队列长度：统计当前排队的元素个数（如 “当前收银台有 6 人在排队”）；
  • 入队：新元素从队尾加入队列（如 “新顾客站到队尾排队”）；
  • 出队：队头元素离开队列（如 “队头的顾客付完钱离开”）；
  • 判队空：判断队列是否无元素（如 “当前收银台是否没人排队，可暂停服务”）；
  • 判队满：判断队列是否达到最大容量（如 “排队通道最多站 10 人，当前是否已满，需引导顾客去其他通道”）；
  • 取队头元素：查看队头元素的值（如 “收银员确认队头是谁，准备为其扫码结算”）。

（2）基本操作的函数实现

• 函数参数与功能的关联：
  • InitQueue (SqQueue &Q)：初始化空队列，参数用引用（&Q）是因为需要修改队列的初始状态（如让队头、队尾指针指向初始位置），若用值传递则无法修改原队列；
  • QueueLength(SqQueue Q)：返回队列元素个数，参数用值传递（Q）是因为仅读取队列信息（不修改队列），无需引用；
  • EnQueue (SqQueue &Q, QElemType e)：将元素 e 插入队尾，引用（&Q）是因为要修改队列的元素数量和队尾指针，e 是待插入的元素值；
  • DeQueue(SqQueue &Q, QElemType &e)：删除队头元素并赋值给 e，引用（&Q）是因为要修改队列的元素数量和队头指针，引用（&e）是因为要将删除的元素值返回给调用者；
  • QueueEmpty(SqQueue Q)：判断队列是否为空，返回 Status 类型（如 OK 表示空，ERROR 表示非空），仅读取队列状态，无需引用；
  • QueueFull(SqQueue Q)：判断队列是否已满，避免入队时溢出（如顺序队列满时无法再插入元素），仅读取队列状态，无需引用；
  • GetHead(SqQueue Q, QElemType &e)：读取队头元素并赋值给 e，不删除元素，因此队列本身不修改（Q 用值传递），引用 e 是为了返回队头元素值；
  • DestroyQueue (LinkQueue &Q)：释放队列占用的存储空间（如链式队列的节点内存），彻底销毁队列，引用（&Q）是因为要修改队列的存在状态（从 “存在” 变为 “销毁”）。

3.4 队列的表示和操作的实现

3.4.1 队列存储结构概述（结合老师讲解补充）

老师开篇明确：队列的存储理论上包含顺序存储、链式存储、索引存储、散列存储4 种，但实际应用中仅需重点掌握顺序存储结构和链式存储结构（索引、散列存储极少用于队列，无需深入）。

3.4.2 顺序队列 —— 队列的顺序存储结构

（1） 定义与核心要素

• 定义：用一组地址连续的存储单元，依次存放从队列头到队列尾的元素，需定义两个关键指针：
  • Q.front：指向队列头元素（当前可出队的元素位置）；
  • Q.rear：指向队列尾元素的下一个位置（当前可进队的空位置，老师强调：此为顺序队列的核心特征，需与 “指向队尾” 严格区分）。
• 初始状态（空队列）：Q.front = Q.rear = 0（课件公式，老师举例：空队列时，两个指针均指向数组起始下标 0，无任何元素）。
• 操作原则（老师总结）：
  1. 进队仅操作Q.rear，出队仅操作Q.front（“各管其事，不交叉”）；
  2. 无论进队还是出队，指针均做 “加 1” 操作（区别于栈的top指针 “加 1 / 减 1” 双向变动）。

（2）进队与出队操作

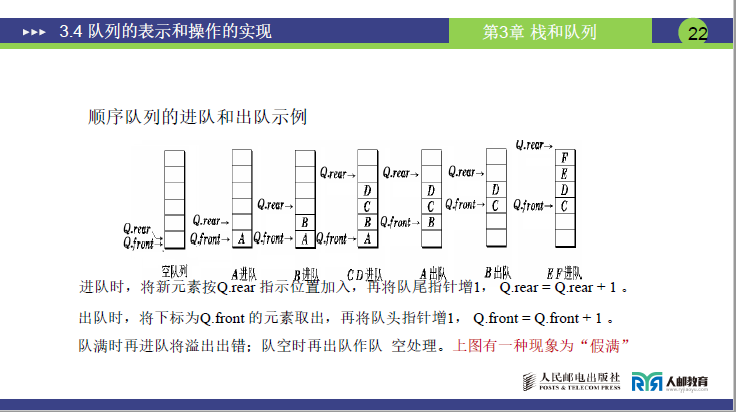
课件示例图（页码 22：顺序队列的进队和出队示例）展示了完整流程，老师结合该图补充细节如下：

1. 空队列初始化：Q.front = Q.rear = 0（指针均指向起始点，数组无元素）；
2. 进队操作（以元素 A、B、C、D 为例）：
   • 步骤：将元素存入Q.rear指向的位置，随后Q.rear += 1（“进队动 rear，rear 加加”）；
   • 过程：
     • A 进队→存到下标 0，rear=1；
     • B 进队→存到下标 1，rear=2；
     • C、D 依次进队后，rear=4（指向 D 的下一个位置，即下标 4）。
3. 出队操作（以元素 A、B 为例）：
   • 步骤：先取出Q.front指向的元素，随后Q.front += 1（“出队动 front，front 加加”）；
   • 过程：
     • A 出队→取下标 0 的 A，front=1；
     • B 出队→取下标 1 的 B，front=2；
     • 最终队列剩余 C、D，front=2，rear=4（元素存于下标 2-3）。

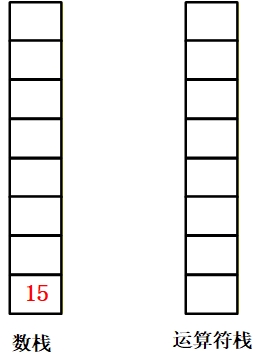
（3） 顺序队列的致命问题 ——“假满” 现象

• 课件定义（页码 22）：当Q.rear达到数组最大下标时，即使Q.front>0（队头有元素出队后空出空间），也无法继续进队，这种 “实际有空间却不能用” 的情况称为 “假满”。
• 老师举例（5 个空间的数组，下标 0-4，maxSize=5）：
  1. 进队阶段：10→下标 0（rear=1）、20→下标 1（rear=2）、30→下标 2（rear=3）、40→下标 3（rear=4）、50→下标 4（rear=5）；此时rear=5（超出数组最大下标 4），看似 “队满”；
  2. 出队阶段：10 出队（front=1）、20 出队（front=2）；此时队列剩余 30、40、50（存于下标 2-4），下标 0-1 空出；
  3. 假满体现：想进 60→rear=5已超数组范围，无法存入，但下标 0-1 实际为空；根源是rear和front“各管其事”，rear到顶后无法复用队头空空间。

3.4.3 链队列 —— 队列的链式存储结构

（1）定义与核心要素（课件内容 + 老师补充）

• 课件定义（页码 23）：实质是带头结点的单链表（头结点不存数据，仅简化操作），设两个指针：
  • Q.front：指向头结点（固定指向头结点，不随元素删除变动）；
  • Q.rear：指向尾结点（最后一个数据结点，随元素插入变动）。
• 初始状态（空队列）：Q.front = Q.rear（均指向头结点，头结点的next为NULL，老师举例：空链队列中无任何数据结点，仅头结点存在）。

（2）链队列的优缺点（老师重点补充）

• 优点：无需预先分配固定空间，理论上可无限存储（只要内存足够），无 “假满” 问题；

• 缺点（老师强调：关键考点）：

  链式存储需额外空间存储 “下一个结点的地址”（指针域），而队列仅允许在队尾插入、队头删除（无需中间位置操作）—— 链式存储 “插入删除无需搬移元素” 的核心优点无法体现，因此实际应用中优先选择顺序队列（循环队列），链队列仅作了解。

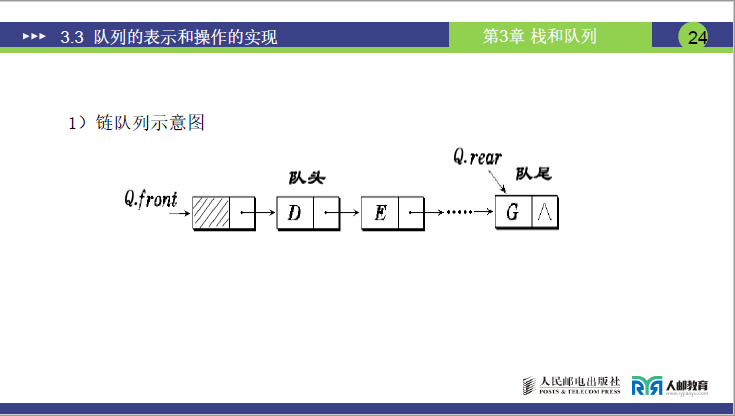
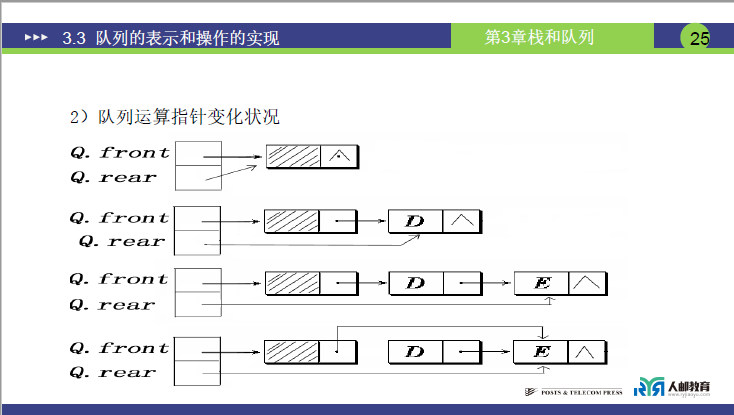
（3）进队与出队操作

课件示意图（页码 24：链队列示意图）：头结点→D→G→A（尾结点），Q.front指向头结点，Q.rear指向 A；老师结合该图拆解操作：

1. 进队操作（插入元素 E）：

   • 核心：仅动Q.rear，将新结点接在尾结点后，更新rear指向新尾结点；

   • 步骤：

     ① 创建数据为 E 的新结点；

     ②Q.rear->next = E（将 E 接在原尾结点 A 后）；

     ③Q.rear = E（更新rear指向 E，E 成为新尾结点）。

2. 出队操作（删除元素 D）：

   • 核心：不动Q.front，仅操作头结点的next（删除队头数据结点）；

   • 步骤：

     ① 暂存队头数据结点（p = Q.front->next，即 D 结点）；

     ②Q.front->next = p->next（头结点直接指向 G，跳过 D）；

     ③ 若 D 是最后一个数据结点（p == Q.rear），则Q.rear = Q.front（避免空队列时rear悬空）；

     ④ 释放 D 结点的内存。

3.4.4 循环队列 —— 解决 “假满” 的核心结构（对应课件页码 26、27、28）

（1） 定义与设计思想（课件内容 + 老师强调）

• 定义：逻辑上将顺序队列的数组视为 “环状”（首尾相连），队头指针front和队尾指针rear到达数组末尾后，可绕回起始位置；不能用动态分配的一维数组实现，初始化必须设定最大队列长度（maxSize）。
• 老师核心强调（考试必记）：不加任何说明时，考试中 “队列” 均指循环队列（不考普通顺序队列），其核心目的是 “复用队头空出的空间，彻底解决假满问题”。
• 实现原理：通过 “取余运算（%）” 实现 “环状跳转”—— 指针加 1 后，若超出数组最大下标，用(指针+1) % maxSize绕回起始位置（例maxSize=10，指针 = 9 时，(9+1)%10=0，绕回下标 0）。

（2）关键问题：队空与队满的判别

• 问题：普通顺序队列中Q.front = Q.rear表示空队列，但循环队列中rear绕回后可能与front重合（如满队时），需明确区分 “空” 和 “满”。
• 课件方案 1（推荐，严蔚敏教材标准，考试重点）：牺牲一个存储单元（不存数据），用以下条件判别：
  • 队空：Q.front == Q.rear（指针重合，无数据）；
  • 队满：(Q.rear + 1) % maxSize == Q.front（rear的下一个位置是front，说明无空空间）。
  • 举例（maxSize=10，数组下标 0-9，牺牲下标 9）：
    • 队空：front=0，rear=0（指针均指向 0，无元素）；
    • 队满：rear=8，(8+1)%10=9，若front=9，则满足 “队满条件”，此时实际存储 9 个元素（maxSize-1=9）。
• 课件方案 2（了解）：设标志变量tag（tag=0表示 “刚出队”，tag=1表示 “刚入队”），Q.front == Q.rear时：tag=0为队空，tag=1为队满；老师说明：考纲不要求，重点掌握方案 1。

（3）循环队列的 6 个核心操作

课件提及 “循环队列的 6 个操作”，结合maxSize=10（数组下标 0-9）的例子，详细推导每个操作的步骤和公式（均基于方案 1：牺牲 1 个空间）：

操作 1：求最大可存储元素数

• 核心结论：maxSize - 1（因牺牲 1 个空间区分空满）；
• 示例：maxSize=15→最大可存 14 个元素（15-1=14）。

操作 2：判队空

• 条件：Q.front == Q.rear；
• 示例：front=2，rear=2→指针重合，队空（无元素）。

操作 3：判队满

• 条件：(Q.rear + 1) % maxSize == Q.front；
• 示例：
  • 若 front=3，rear=8→(8+1)%10=9 ≠ 3→未满；
  • 若 front=3，rear=2→(2+1)%10=3 == 3→队满（元素存于下标 3-2 的环状区域：3、4、5、6、7、8、9、0、1）。

操作 4：入队（EnQueue，存元素 e）

• 步骤：
  1. 判队满：若满则报 “上溢” 错误；
  2. 将 e 存入Q.rear指向的位置（rear本就指向可存元素的空位置）；
  3. 更新rear：Q.rear = (Q.rear + 1) % maxSize（实现环状跳转）；
• 示例：front=2，rear=8，入队元素 K：
  1. (8+1)%10=9 ≠ 2→未满；
  2. 将 K 存入下标 8（rear当前值）；
  3. rear=(8+1)%10=9→更新后rear=9。

操作 5：出队（DeQueue，取队头元素）

• 步骤：
  1. 判队空：若空则报 “下溢” 错误；
  2. 暂存队头元素：e = Q.data[Q.front]（Q.data为存储数组）；
  3. 更新front：Q.front = (Q.front + 1) % maxSize（实现环状跳转）；
• 示例：front=2，rear=9，出队：
  1. front=2 ≠ rear=9→非空；
  2. 取出下标 2 的元素（队头）；
  3. front=(2+1)%10=3→更新后front=3。

操作 6：求实际元素个数（队列长度）

• 老师推导公式（统一两种场景）：

  场景 1：rear > front→元素数 = rear - front；

  场景 2：rear < front→元素数 =（rear + maxSize） - front；合并公式：length = (Q.rear + maxSize - Q.front) % maxSize；

• 示例：

  • 场景 1：front=4，rear=7→(7+10-4)%10=13%10=3→3 个元素（下标 4、5、6）；
  • 场景 2：front=6，rear=2→(2+10-6)%10=6%10=6→6 个元素（下标 6、7、8、9、0、1）。

（3）循环队列完整示例

以maxSize=10为例，演示循环队列解决 “假满” 的全过程：

1. 初始化：front=0，rear=0（空队列）；

2. 进队 9 个元素（A-I）：

   每个元素进队后rear加 1（取余），最终rear=(0+9)%10=9；此时(9+1)%10=0 == front=0→队满（存 9 个元素，符合 maxSize-1=9）；

3. 出队 2 个元素（A、B）：每个元素出队后front加 1（取余），最终front=(0+2)%10=2；此时front=2 ≠ rear=9→非空；

4. 进队元素 K：

   • 判满：(9+1)%10=0 ≠ 2→未满；
   • 存 K 到下标 9（rear当前值）；
   • 更新rear=(9+1)%10=0；
   • 结果：队列元素为 C、D、E、F、G、H、I、K（8 个），rear=0，front=2；下标 0、1 空出（后续可继续进队元素存于 0、1），彻底解决 “假满”。

3.4.5 队列基本操作函数汇总

操作功能	课件函数声明	核心说明（结合老师讲解）
初始化队列	Status InitQueue(SqQueue &Q)	循环队列需额外初始化maxSize，设Q.front=Q.rear=0
求队列长度	int QueueLength(SqQueue Q)	循环队列必须用公式(Q.rear+maxSize-Q.front)%maxSize
入队	Status EnQueue(SqQueue &Q, QElemType e)	循环队列需先判满，更新rear用(rear+1)%maxSize
出队	Status DeQueue(SqQueue &Q, QElemType &e)	循环队列需先判空，更新front用(front+1)%maxSize
判队空	Status QueueEmpty(SqQueue Q)	所有队列统一条件：Q.front == Q.rear
判队满	Status QueueFull(SqQueue Q)	仅循环队列需用：(Q.rear+1)%maxSize == Q.front
取队头元素	Status GetHead(SqQueue Q, QElemType &e)	判空后取Q.data[Q.front]，不修改front
销毁队列	Status DestroyQueue(LinkQueue &Q)	链队列需释放所有结点（头结点 + 数据结点），顺序队列无需销毁（数组自动释放）

3.4.6 核心总结（重点）

1. 队列本质：先进先出（FIFO）的线性表，仅允许 “队头删除、队尾插入”；
2. 存储选择：优先用顺序存储（循环队列），链队列仅作了解（优点未体现）；
3. 循环队列（考试核心）：
   • 关键公式：队满(rear+1)%maxSize==front、长度(rear+maxSize-front)%maxSize；
   • 核心思想：牺牲 1 个空间区分空满，取余运算实现环状跳转；
   • 考试约定：不加说明 “队列” 即指循环队列；
4. 常见问题：顺序队列的 “假满”（循环队列解决）、链队列的指针管理（front指头结点，rear指尾结点）。

参考资料：教材《数据结构 C 语言 第 3 版》 数据结构考研指导（基础篇） 、数据结构考研指导（基础篇） 视频课程｜赵海英