第2章线性表
第2章线性表

2.1 线性表的类型定义
2.1.1 线性结构的特点

- 该内容的三重核心作用(考研高频考点):
- 是 “线性结构” 的定义:满足这 4 个特点的数据结构,即为线性结构;
- 是 “线性结构” 的特点描述:直接对应 “线性结构有哪些特点” 类考题;
- 是 “判断结构类型” 的依据:比如判断 “栈是否是线性结构”—— 栈符合这 4 个特点(有唯一开始 / 终端节点,除首尾外元素前驱后继唯一),因此是线性结构。
- 序列图示的具体示例:
a₁→a₂→a₃→…→aₙ- 开始结点a1:仅存在后继(a2),无前驱;
- 终端结点an:仅存在前驱(an−1),无后继;
- 中间结点(如a3):前驱是a2、后继是a4,且仅各有一个;
- 元素关系本质:“一对一” 的线性关系。
2.1.2 线性表

-
线性表的定义细节:
- n≥0:包含 “空表”(n=0时无元素);
- “有限序列”:元素个数有限,且顺序固定。
-
与线性结构的关系:
线性表是线性结构的一种(是 “最简单、最常用” 的线性结构),但不能反向表述为 “线性结构就是线性表”—— 因为线性结构还包含栈、队列等类型。
-
数据结构List=(D,R)的具体含义:
- 数据集合D:
- 元素是 “数据元素”(不是 “数据项”):比如 “学生表” 中,每个a**i是 “一个学生的完整信息”(含姓名、学号等),而非单个字段;
- 均匀性:所有ai是同类型、同结构的数据元素(比如学生表中每个元素都是 “学生” 类型)。
- 关系集合R:
- R是 “有序对偶对” 的集合:比如i=2时,对偶对是<a1,a2>;i=3时是<a2,a3>,以此类推;
- 有序性:对偶对的顺序固定,体现了线性表的 “线性序列关系”(元素按a1→a2→…→an的顺序排列)。
- 数据集合D:
2.1.3 线性表的基本操作

| 操作序号 | 函数名 | 操作名称 | 核心功能 | 关键细节 |
|---|---|---|---|---|
| 1 | InitList(&L) | 初始化 | 构造一个空的线性表 | 操作起点,初始化后表长为 0 |
| 2 | ListLength(L) | 求长度 | 计算线性表中数据元素的个数 | 返回值为n(n≥0),是空表判断、插入 / 删除位置合法性校验的基础 |
| 3 | GetElem(L,i,&e) | 读取(取元素) | 取出第i个位置的元素,赋值给变量e |
属于 “读操作”,不修改表内容;需先判断i的合法性(1 ≤ i ≤ n) |
| 4 | LocateElem(L,e) | 按值查找 | 给定值e,查找其在表中的位置(序号) |
找到返回位置i,未找到返回 “特殊值”(如 0 或 - 1,需提前约定);默认返回第一个匹配元素 |
| 5 | ListInsert(&L,i,e) | 插入 | 在第i个位置之前插入新元素e |
插入后表长n = n+1;“在第i个位置之后插入” 可转化为 “在第i+1个位置之前插入” |
| 6 | ListDelete(&L,i,e) | 删除 | 删除第i个位置的元素,并返回该元素的值 |
删除后表长n = n-1;需先判断i的合法性(1 ≤ i ≤ n),空表不可删除 |
2.2 线性表的顺序表示和实现
2.2.1前置知识回顾
-
逻辑结构与存储结构的关系:
-
一个问题的逻辑结构是唯一的,分为两大类:
- 线性结构(一对一关系);
- 非线性结构(树:一对多;图:多对多)。
-
存储结构(又称物理结构)不唯一,共 4 类:
顺序存储、链式存储、索引存储、散列存储;
本章仅学习前 2 类,后 2 类将在 “查找 / 排序” 章节讲解。
-
存储结构的选择由需求决定(如 “节省空间” 或 “提升速度”),不同选择会直接影响算法效率。
-
2.2.2线性表的顺序存储结构(简称:顺序表,也叫 “顺表”)

对应课件 “存储结构 顺序表 — 线性表的顺序存储结构” 板块
(1) 顺序表的核心定义
定义:“用‘物理位置’相邻来表示线性表中数据元素之间的逻辑关系”
- 解释:线性表中逻辑上相邻的元素(如 a₁的后继是 a₂、aᵢ的前驱是 aᵢ₋₁),在物理存储(内存)中,位置也必须相邻(即 “逻辑相邻 → 物理相邻”)。
(2)顺序表的存储原理(对应课件第 6 页右侧的顺序表存储示意图)
- 内存的 2 个关键特点:
- 内存是一维、线性的存储空间;
- 内存通过 “地址值(门牌号)” 寻址,“内容值(数据)” 存在对应地址中,地址与数据通过不同总线传输(地址总线、数据总线)。
- 举例(线性表数据:[10,20,30,40,50]):
- 逻辑结构:典型线性结构(一对一关系,10 是首元素仅含后继,50 是尾元素仅含前驱);
- 物理存储:10 存入某起始地址后,20 必须存在 10 的相邻下一个地址,30 存于 20 之后…… 与逻辑结构的相邻关系完全一致(对应课件图中连续的存储单元)。
(3)顺序表的随机存取特性
对应课件要点 2:“只要确定了存储线性表的起始位置,线性表中任一数据元素都可随机存取,所以是一种随机存取的存储结构”
- 老师解释:类似电影院找座位(知道 15 排的位置,可直接定位 17 排)—— 只要确定顺序表的起始地址,结合元素的索引(位置),能直接计算出目标元素的地址,无需依次遍历,因此查找(查询)操作效率高。
2.2.3 顺序表的优缺点(老师扩展内容)
(1)优点
- 随机存取:查找(查询)操作效率高,无需移动元素,通过地址计算可直接定位目标。
(2)缺点
-
插入、删除操作效率低(需大量元素移动):
-
插入例子(老师举例:在 30 和 40 之间插入 35):
因要求 “逻辑相邻→物理相邻”,需先将 40、50 依次向后移动,空出 30 后的位置,才能存入 35,会产生元素移动操作。
-
删除例子(老师举例:删除 20):
需将 20 之后的 30、40、50 依次向前移动,覆盖 20 的位置,同样产生大量元素移动。
- 本质原因:顺序表要求元素存储连续,插入 / 删除会破坏连续性,需通过元素移动恢复连续,导致效率降低。
-
2.2.4 过渡
为解决顺序表 “插入、删除效率低” 的问题,后续将学习线性表的第二种存储结构:链式存储。
2.3 线性表的链式表示和实现
2.3.1 链式存储的引入背景
顺序表的核心痛点是插入 / 删除操作需移动大量元素(时间复杂度 O (n)),例如在长度为 1000 的顺序表中插入一个元素,平均需移动 500 个元素。讲课中赵老师提出:“若能不移动元素,仅通过修改‘指向关系’实现插入删除,效率就能提升到常数级(O (1))”—— 这就是链式存储的设计初衷。
要存储线性表(10,20,30,40),内存中找不到 4 个连续的存储单元(如 10001 被占用、10002 空闲、10003 空闲、10004 被占用),顺序表无法存储;但链式存储可利用零散空间(如 10001 存 10、10005 存 20、10003 存 30、10006 存 40),通过 “指针” 记录下一个元素的位置,完美解决空间不连续问题。
2.3.2 链表的存储结构

(1)课件核心内容
链表是线性表的链式存储结构,特点:
- 用一组任意的存储单元(连续或不连续均可)存储数据元素;
- 每个数据元素的存储映像称为 “节点”,节点由两部分组成:
- 数据域:存储元素的值(如 10、20);
- 指针域(链域):存储后继元素的存储位置(地址);
- n 个节点通过指针链接成链表,仅含一个指针域的链表称为 “线性链表(单链表)”。
(2)讲课内容补充扩展
- “任意存储单元” 的深层含义:与顺序表 “逻辑相邻→物理必相邻” 不同,链表的逻辑相邻(如 10 在 20 前面)不依赖物理位置相邻,只要通过指针能找到下一个元素即可。赵老师举例:10 存在地址 10001(物理位置 1)、20 存在 10005(物理位置 5),二者物理不相邻,但 10 的指针域存 10005,逻辑上仍是相邻的。
- 指针的本质:“指针就是存储地址的变量,节点的指针域存的是‘下一个节点的门牌号’”。例如 10 的指针域存 10005,就像 “1 号房子的门后贴了 5 号房子的地址”,通过 1 号能找到 5 号。
- 空间代价与时间收益:链表比顺序表多占用指针域的空间(如每个节点多存 4 字节地址),但换来了插入 / 删除无需移动元素的时间优势,属于 “空间换时间” 的经典设计。
2.3.3 单链表(Singly Linked List)
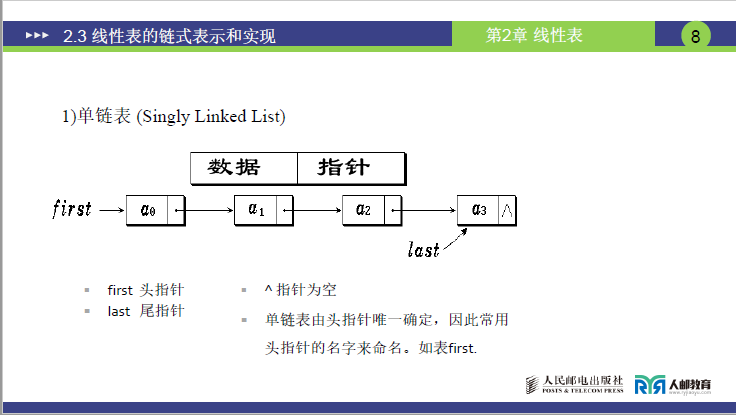
(1)单链表的结构(对应课件第 8 页,单链表逻辑示意图)
①课件核心内容
- 单链表由头指针(first) 唯一确定:头指针指向链表的第一个节点;
- 最后一个节点称为 “尾节点(last)”,其指针域为空(记为
^或NULL); - 单链表的名称以头指针命名(如 “表 first”)。
②结合 “链子” 类比与具体地址实例
- 将单链表比作 “串起来的珠子”:“每个珠子是节点(数据 + 指针),绳子是指针关系,第一个珠子的位置由‘头指针’记录,最后一个珠子没有下一个,所以绳子断了(指针 NULL)”。
- 为什么叫 “单” 链表?“因为每个节点只有一个指针,只能指向后继,不能指向前驱,就像人只能往前走,不能往后退”。
③实例解析

假设存储线性表(10,20,30,40),头指针 first 指向 10 的地址 10001,各节点的存储情况:
| 内存地址 | 数据域(内容) | 指针域(下一个地址) | 角色 |
|---|---|---|---|
| 10001 | 10 | 10005 | 第一个节点 |
| 10005 | 20 | 10003 | 中间节点 |
| 10003 | 30 | 10006 | 中间节点 |
| 10006 | 40 | NULL | 尾节点 |
- 遍历过程:从 first(10001)出发→取 10→通过指针 10005 找到 20→通过 10003 找到 30→通过 10006 找到 40→遇到 NULL 停止,完成全表遍历。
(2)单链表的存储映像
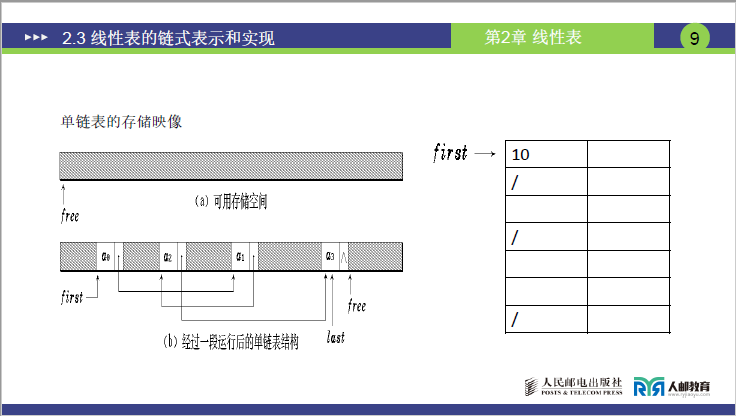
①课件图示说明
- 图(a):可用存储空间(free 区域):展示未存储数据时,内存单元(如地址 01、02、43、10 等)处于空闲状态,头指针 first 未指向任何有效节点,free 指针指向空闲区域的起始位置。
- 图(b):经过一段运行后的单链表结构:头指针 first 指向地址 10(存储数据 10),10 的指针域指向地址 02(存储数据 20),20 的指针域指向地址 43(存储数据 30),30 的指针域指向 free 区域(后续可存储新节点),尾节点(暂为 30)的指针域待补充新节点后指向 NULL。
②对图示的通俗解释
- 图(a)的 “free”:“就像空的房间,门牌号(地址)01、02、43 都没人住,free 是‘房东’,记录第一个空房间的位置”。
- 图(b)的 “运行后结构”:“我们租了 10、02、43 三个房间存 10、20、30,‘头指针’first 知道第一个房间是 10,10 房间的门上贴了 02 的地址,02 贴了 43 的地址,43 暂时没贴(指向 free),等存 40 时,43 贴 40 的地址,40 贴 NULL”。
2.3.4 带头结点的单链表
(1)结构定义
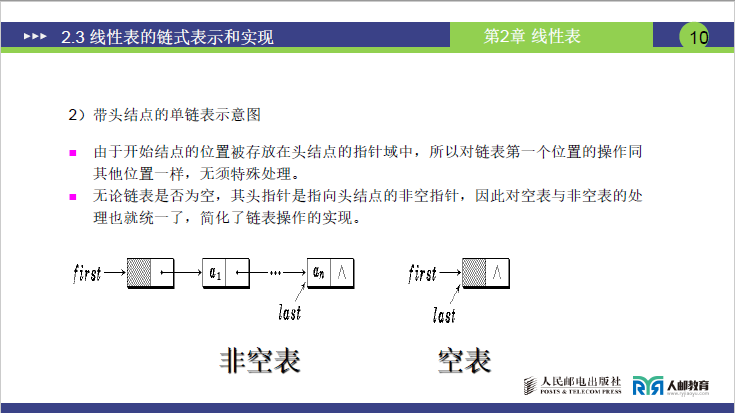
①课件核心内容
- 在单链表第一个节点前增加 “头节点”:头节点的数据域为空(或存储链表长度等辅助信息),指针域指向真正的第一个节点;
- 无论链表是否为空,头指针 first 始终指向头节点(非空指针),尾指针 last 指向尾节点(空表时 last 也指向头节点)。
②讲课内容补充(头节点的 “反直觉” 设计与实例)
-
赵老师提出疑问:“头节点数据域为空,还占一个空间,是不是浪费?其实是为了‘省事’”—— 举了两个关键场景:
-
空表的表示:空表时,头节点的指针域为 NULL,first 和 last 都指向头节点(如下图),“不用判断 first 是不是 NULL,只要看头节点指针域是不是 NULL 就行”。
first → [空(数据域)| NULL(指针域)] ← last -
初始化实例:存储(10,20,30,40)的带头结点单链表,地址用 1-7 简化:
地址 数据域 指针域(下一个地址) 角色 1 空 3 头节点 3 10 7 第一个节点 7 20 2 中间节点 2 30 5 中间节点 5 40 NULL 尾节点 - 初始化步骤:“先创头节点(地址 1),数据空,指针指 3(10 的地址);10 的指针指 7(20 的地址),20 指 2(30),30 指 5(40),40 指 NULL”,赵老师强调 “不能按地址顺序填,要按数据的逻辑顺序填”。
-
(2)带头结点单链表的插入

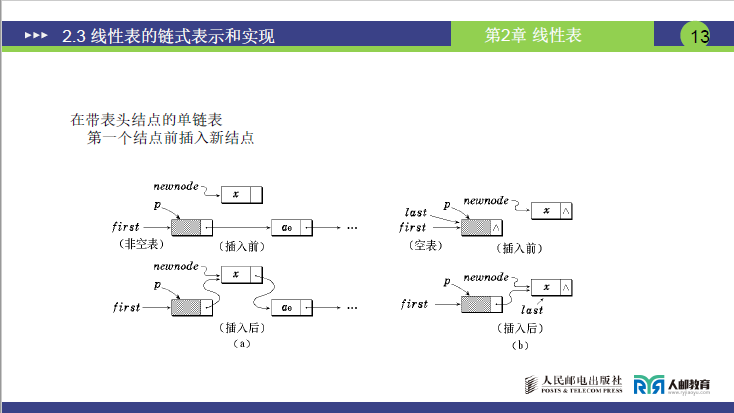
①课件图示说明
- 带头结点单链表插入图:展示在头节点与第一个节点之间(或中间位置)插入新节点的过程,新节点的指针域先指向原后继节点,再修改前驱节点的指针域指向新节点。
- 在带表头结点的单链表第一个结点前插入新结点图(a)(b):
- 图(a):非空表插入前(first→头节点→a₀),插入后(first→头节点→newnode→a₀);
- 图(b):空表插入前(first→头节点,头节点指针域 NULL),插入后(first→头节点→newnode,newnode 指针域 NULL)。
②讲课内容补充(插入 35 的详细实例,重点讲解)
场景:在 30(地址 2)和 40(地址 5)之间插入 35,空地址选 6。

开始链表为 “头节点(1)→10(3)→20(7)→30(2)→40(5)→NULL”
步骤(对应第 11 页插入图):
- 找空地址:选择 6 号地址,数据域填入 35(“先把 35 住进 6 号房”);
- 先连后断(核心原则):
- 连:35 的指针域 = 30 原指针域(即 40 的地址 5)——“6 号房贴 5 号的地址,保证能找到 40”;
- 断:30 的指针域 = 新节点地址 6——“2 号房(30)原本贴 5 号,现在改贴 6 号,把 35 串进来”;
- 结果:链表变为 “头节点(1)→10(3)→20(7)→30(2)→35(6)→40(5)→NULL”,无任何元素移动,仅修改 2 个指针。

赵老师强调的易错点:“必须先连后断!如果先改 30 的指针到 6,再找 40 的地址就丢了,链表会断成两截”。
(3)带头结点单链表的删除

①课件图示说明
- 第 11 页:带头结点单链表删除图:展示删除第一个节点(a₀)的过程,头节点的指针域原本指向 a₀,删除后指向 a₁,a₀节点被释放。
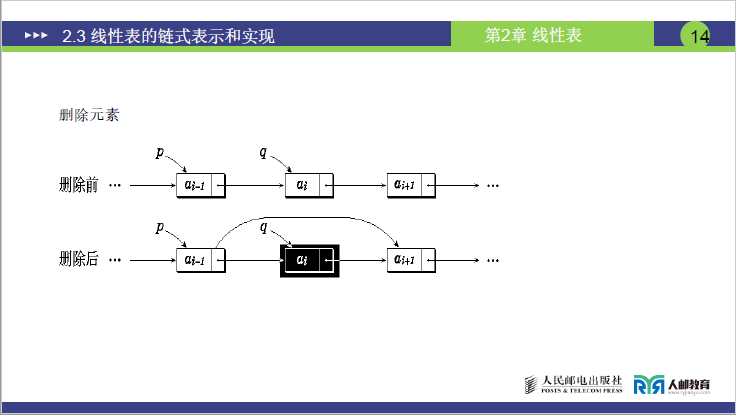
- 第 14 页:删除元素图:删除前(...aᵢ₋₁→aᵢ→aᵢ₊₁...),删除后(...aᵢ₋₁→aᵢ₊₁...),p 指向 aᵢ₋₁,q 指向 aᵢ。
②讲课内容补充(删除 30 的详细实例,含内存泄露提醒)
场景:删除 30(地址 2),链表变为(10,20,40)。
步骤(对应第 12 页删除图):
- 找前驱节点:找到 30 的前驱 20(地址 7)——“要删 30,必须先找到它前面的 20,因为单链表只能从前向后找”;
- 迈过删除节点:20 的指针域 = 30 的指针域(即 40 的地址 5)——“7 号房(20)原本贴 2 号,现在改贴 5 号,直接跳过 2 号房(30)”;
- 释放空间(关键补充):赵老师强调 “考试中写步骤到这就行,但实际编程要加
delete释放 2 号地址的空间”——“如果不释放,2 号房一直被 30 占着,内存越用越少,电脑会变慢(内存泄露)”; - 结果:链表变为 “头节点(1)→10(3)→20(7)→40(5)→NULL”,仅修改 1 个指针,无元素移动。
(4)带头结点的优点

①课件核心问题
- 考题 1:带头结点的单链优点;
- 考题 2:为什么引入带头结点的单链。
②讲课内容补充(赵老师的 “编程简化” 解释)
赵老师总结两大核心优点,结合编程场景说明:
- 统一插入 / 删除操作:
- 无表头时:插入第一个节点需修改头指针(first→新节点),插入中间节点需修改前驱指针(aᵢ₋₁→新节点),需写两个
if判断; - 有表头时:所有插入都修改前驱指针(头节点是第一个节点的 “虚拟前驱”),无需区分 “表头” 和 “中间”,代码少一个
if嵌套。
- 无表头时:插入第一个节点需修改头指针(first→新节点),插入中间节点需修改前驱指针(aᵢ₋₁→新节点),需写两个
- 统一空表与非空表处理:
- 无表头时:空表(first=NULL)、非空表(first→第一个节点),需判断 first 是否为 NULL;
- 有表头时:空表(头节点指针域 = NULL)、非空表(头节点指针域→第一个节点),只需判断头节点指针域,代码更简洁。
2.3.5 循环链表
(1)结构定义

①课件核心内容
- 循环链表是首尾相接的链表:尾节点的指针域不为 NULL,而是指向头节点;
- 通常加入头节点,简化操作;
- 特点:从任一节点出发可访问到表中所有节点(单链表需从头指针开始)。
②讲课内容补充(“环” 的类比与实例)
- 赵老师类比:“单链表是‘直线’,到尾节点就停了;循环链表是‘圆圈’,从任何一个节点出发都能绕一圈回到自己”。
- 实例:存储(10,20,30,40)的循环链表,头节点地址 1,尾节点 40(地址 5)的指针域指向头节点 1,而非 NULL。遍历过程:从 20(地址 7)出发→30(2)→40(5)→头节点(1)→10(3)→20(7),形成闭环。
(2)循环链表与单链表的区别
①课件图示说明
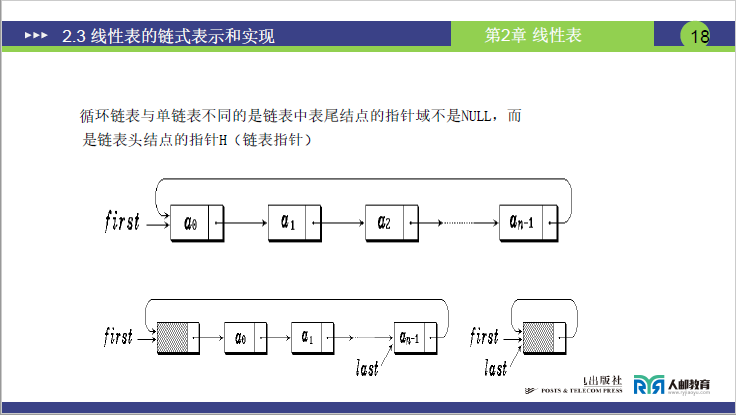
- 图中展示:单链表尾节点指针域 = NULL,循环链表尾节点指针域 = 头节点指针 H(first);
- 左侧:first→a₀→a₁→a₂→aₙ₋₁(尾节点指针 NULL);
- 右侧:a₀→a₁→...→aₙ₋₁→first(尾节点指针指向 first)。
②讲课内容补充(空表判断与遍历终止条件)
- 空表判断:循环链表空表时,头节点的指针域指向自身(first→头节点→first),“不像单链表头节点指针域 NULL,而是自己指自己,说明没其他节点”;
- 遍历终止条件:单链表是 “p!=NULL”,循环链表是 “p!=first”——“如果用 p!=NULL,会一直绕圈(死循环),因为没有 NULL”。
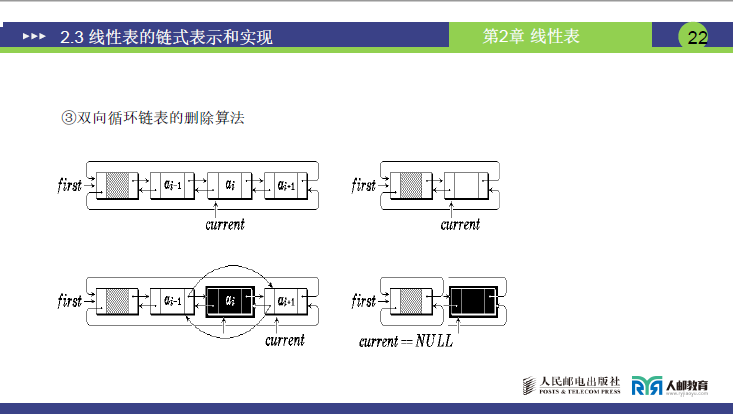
2.3.6 双向链表(Doubly Linked List)
(1)双向链表的节点结构

①课件核心内容
- 双向链表的节点含三个部分:
- 前驱指针域(prior):存储前驱节点的地址;
- 数据域(data):存储元素值;
- 后继指针域(next):存储后继节点的地址;
- 支持 “前驱方向遍历” 和 “后继方向遍历”(单链表仅支持后继方向)。
②讲课内容补充(“前后都能走” 的优势)
- 举例:“在单链表中,站在 30(地址 2)的位置想找 20(地址 7),必须从头指针 first 开始;但双向链表中,30 的 prior 指针直接存 7,一步就能找到 20,就像人既能往前走,也能往后退”;
- 空间代价:“每个节点多存一个 prior 指针(如 4 字节),空间开销比单链表大,但访问效率更高,是‘空间换时间’的再体现”。
(2)双向循环链表的插入
①课件图示说明
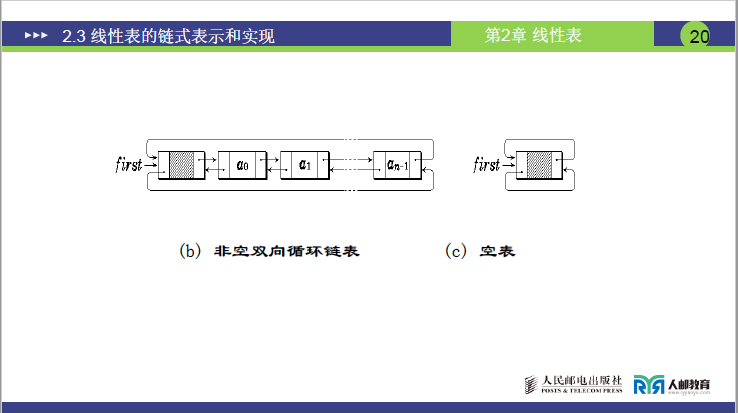
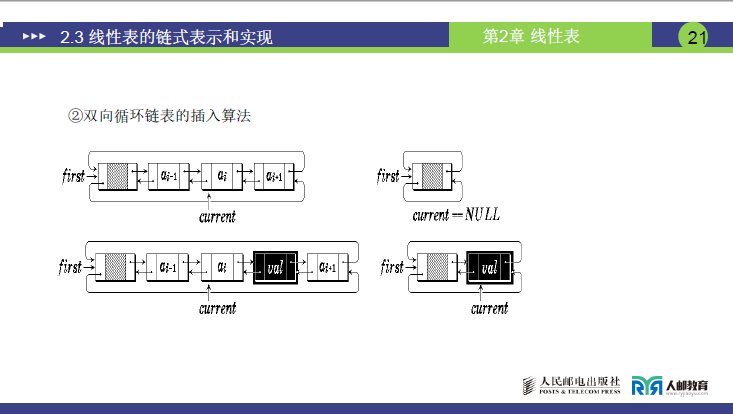
- 图中展示:插入前(first→aᵢ₋₁→aᵢ→aᵢ₊₁→first),插入后(first→aᵢ₋₁→val→aᵢ→aᵢ₊₁→first);
- current 指针初始指向 aᵢ(或 NULL,空表时),插入后 val 的 prior 指向 aᵢ₋₁,next 指向 aᵢ,aᵢ₋₁的 next 指向 val,aᵢ的 prior 指向 val。
②讲课内容补充(插入 val 的四步操作,赵老师总结)
场景:在 aᵢ₋₁(地址 7,数据 20)和 aᵢ(地址 2,数据 30)之间插入 val(35,地址 6)。
四步操作(对应第 21 页图):
- 新节点 val 的 prior = aᵢ₋₁的地址 7——“35 的 prior 贴 7,知道前面是 20”;
- 新节点 val 的 next = aᵢ的地址 2——“35 的 next 贴 2,知道后面是 30”;
- aᵢ₋₁的 next = val 的地址 6——“20 的 next 贴 6,改指向 35”;
- aᵢ的 prior = val 的地址 6——“30 的 prior 贴 6,改指向 35”;
- 强调:“四步不能乱!必须先连新节点的 prior 和 next,再改原节点的指针,否则会丢地址”。
参考资料:教材《数据结构 C 语言 第 3 版》 数据结构考研指导(基础篇) 、数据结构考研指导(基础篇) 视频课程|赵海英


 浙公网安备 33010602011771号
浙公网安备 33010602011771号