30.快速排序

30.快速排序

算法思想时这样的：

1.每次选取第一个数为基准数；

2.然后使用“乾坤挪移大法”将大于和小于基准的元素分别放置于基准数两边；

3.继续分别对基准数两侧未排序的数据使用分治法进行细分处理，直至整个序列有序。对于下面待排序的数组:

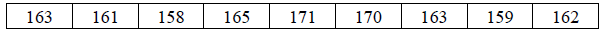
第一步：先选择第一个数163 为基准数，以163 为基准将小于它的数排在它前面，大于等于它的数排在其后，结果如下:

具体排列数据的步骤如下：

1.确定163 为基准数后，先把163 从数组中取出来

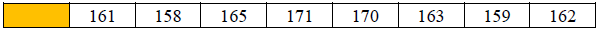
2.然后从最右端开始，查找小于基准数163 的数，找到162，将其移至空出来的元素中

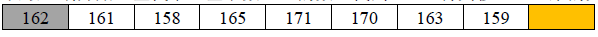
3.接下来，从最左边未处理的元素中从左至右扫描比基数163 大的数，将其移动至右侧空出来的元素中

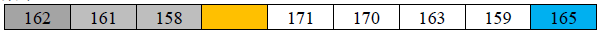
4.接下来，继续从最右边未处理的元素中从右至左扫描比基数163 小的数，将其移动至左侧空出来的元素中

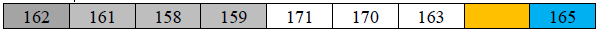
接下来再重复执行步骤3，171 执行右移

重复执行步骤4，此时右边的值已经均大于基数，左边的值均已小于基数

接下来我们将基数保存回黄色空格中

第二步：采用分治法分别对基数左边和右边的部分运用第一步中的方法进行递归操作，直到整个数组变得有序，以左边的数组为例:

选择162 为基数，运用“乾坤挪移大法”得到结果如下:

以162 为界，把数组分成两个部分，此时，基数右侧已经没有数据，所以，接下来只要继续对左侧的数组分治处理即可，选择159 为基数，再次运用“乾坤挪移大法”得到结果如下:

代码实现：

#include <iostream>
#include <stdio.h>
#include <stdlib.h>
using namespace std;

int partition(int arr[], int low, int high)
{
	int i = low;
	int j = high;
	int base = arr[low]; // 1. 选定基准，形成第一个坑 arr[low]

	if (low < high)
	{
		while (i < j) // 只要 i 和 j 没相遇，就一直找
		{
			// 2. 从右向左找，找比 base 小的数
			while (i < j && arr[j] >= base)
			{
				j--;
			}

			// 3. 找到了小的，填入左边的坑 arr[i]
			if (i < j)
			{
				arr[i++] = arr[j]; // 填完坑后，i 向右走一步
			}

			// 4. 从左向右找，找比 base 大的数
			while (i < j && arr[i] < base)
			{
				i++;
			}

			// 5. 找到了大的，填入右边的坑 arr[j]
			if (i < j)
			{
				arr[j--] = arr[i]; // 填完坑后，j 向左走一步
			}
		}

		// 6. 循环结束，i 和 j 相遇，把基准数填入最后的坑
		arr[i] = base;
	}

	return i; // 返回基准数最终所在的下标
}

void QuickSort(int* arr, int low, int high)
{
	if (low < high) // 递归出口：如果只有一个元素或没有元素，就不排了
	{
		// 1. 先进行一轮分区，拿到基准数的位置 index
		// 例如：[3, 1, 5, 9]，index 会是 2 (对应数字 5)
		int index = partition(arr, low, high);

		// 2. 递归处理基准数“左边”的一堆数
		// 处理 [0] 到 [index-1]
		QuickSort(arr, low, index - 1);

		// 3. 递归处理基准数“右边”的一堆数
		// 处理 [index+1] 到 [high]
		QuickSort(arr, index + 1, high);
	}
}

int main()
{
	int arr[] = { 163, 161, 170, 158, 165, 171, 170, 163, 159, 162 };
	int len = sizeof(arr) / sizeof(arr[0]);

	int index = partition(arr, 0, len - 1);
	printf("分区完毕， 基数下标: %d\n", index);

	QuickSort(arr, 0, len - 1);
	printf("执行快速排序后的结果：\n");
	for (int i = 0; i < len; i++)
	{
		printf(" %d", arr[i]);
	}
	cout << endl;

	system("pause");
	return 0;
}

参考资料来源：

奇牛学院