DP(动态规划)--解决最大连续子序和

【题目简述】对于一个给定的长度为N的整数序列A，它的“子序列”的定义是：A中非空的一段连续的元素（整数）。你要完成的任务是，在所有可能的子序列中，找到一个子序列，该子序列中所有元素的和是最大的（跟其他所有子序列相比）。程序要求你输出这个最大值。

输入

【输入测试】输入文件的第一行包含一个整数N，第二行包含N个整数，表示A。 
其中 
1  < =  N  < =  100000 
-10000  < =  A[i]  < =　　10000 

输出

输出仅包含一个整数，表示你算出的答案。 

【样例输入】

7 
1 2 -5 3 8 -3 9

【样例输出】

17
【题目分析】
我们可以把此列数据 当做数组，并且把数组分解为更加小的数组来解决
1.最开始 把 1单独看做一个数组   最大值为：1
2.之后把1 2 看做一个数组   max=3  //max（1+2,2）
3.把1,2，-5 看做一个数组  max=3   // max（-5+3,-5）
4.把1,2，-5,3看做一个数组  max=3   //max（-2+3,3）
5.把1,2，-5，3,8看做一个数组，max=11 //max（3+8,8）
6.把1,2，-5,3,8，-3看做一个数组，max=11  //max（-3+11,-3）
7.把1,2，-5,3,8，-3,9看做一个数组，max=17  //max（9+8,9）
-----------------------------------------------------------
没错：我们可以定义两个数组分别用来存放序列a[n]，和子数组dp[n]的最大值，由上面7步，可以得出
[敲黑板]    dp[i]=max(dp[i-1]+a[i],a[i]);  //如果不懂可以自己在草稿纸上面计算一下

[源代码实现]

#include<iostream>
#include<cstring>
using namespace std;
    int dp[105];
    int num[105];
    int ma;
int main(){
    int n,m;
    memset(dp,0,sizeof(dp));
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>num[i];
    }
    for(int i=1;i<=n;i++){
        dp[i]=max(dp[i-1]+num[i],num[i]);
    }
    ma=dp[0];
    for(int i=1;i<=n;i++){
        //cout<<dp[i]<<" ";
        if(dp[i]>ma){
            ma=dp[i];
        }
    }
    cout<<ma;
    return 0;
}

　　【运行结果】

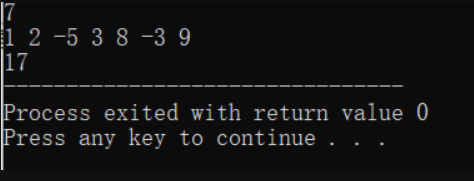
本代码在DevC++下测试通过，如有错误欢迎指正！！！