第五次作业----线性回归算法

1.本节重点知识点用自己的话总结出来，可以配上图片，以及说明该知识点的重要性

首先明白回归算法的概念：就是确定变量之间的关系，建立数学模型去预测真实值。

其次要知道线性回归：指的是自变量和因变量存在线性关系，进行建模的回归方法。根据自变量的个数，又可以分为一元线性回归和多元线性回归。

通过下面的线性关系模型，当我们输入特征值，就能够得出目标值。

 

 而我们需要使用线性回归的话，就要知道什么是矩阵，因为矩阵运算满足了线性回归的需求。

矩阵必须是二维的，有行有列。

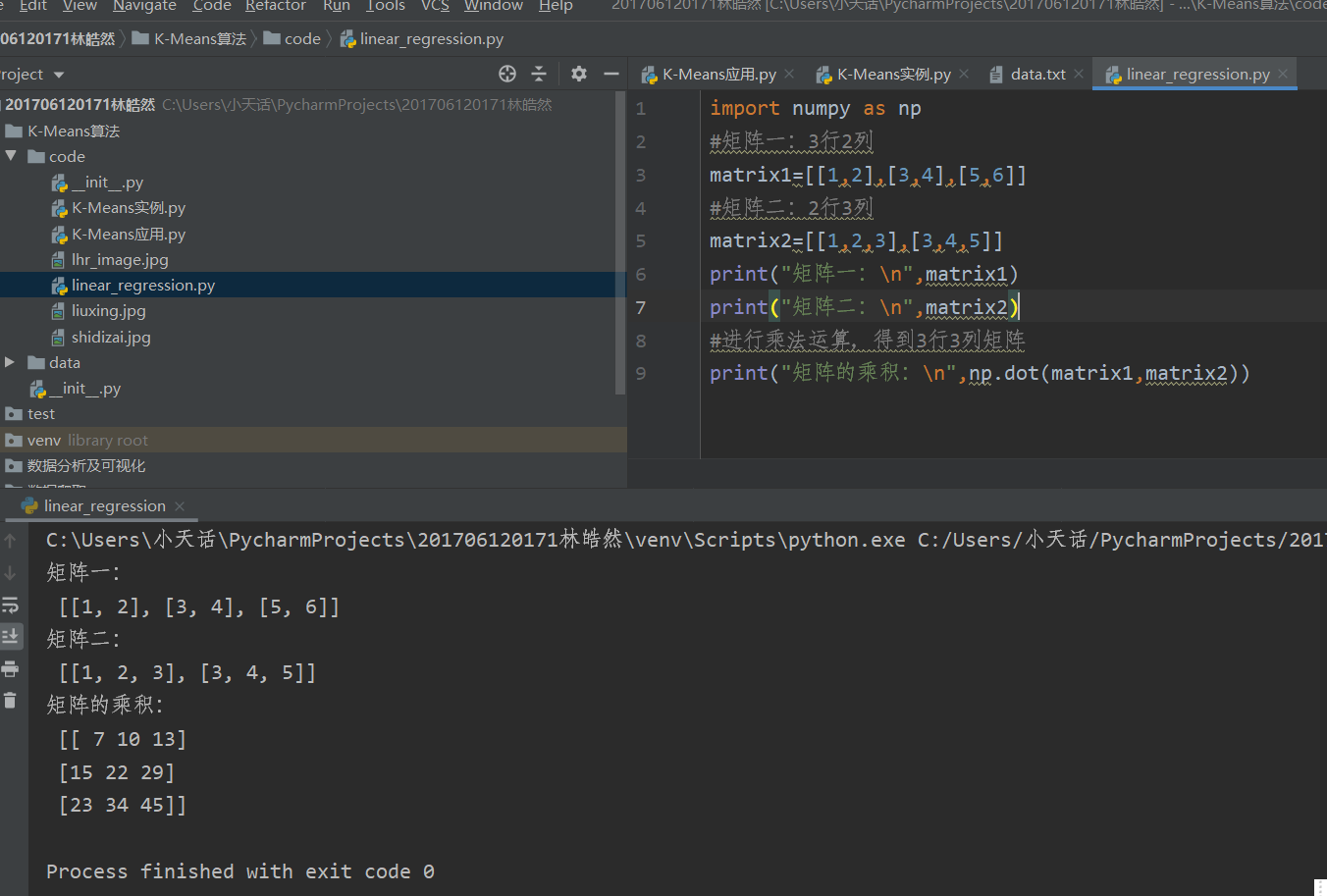
矩阵的乘积运算：

m行h列*h行n列=m行n列的矩阵

举个例子：3行2列矩阵*2行3列矩阵=3行3列矩阵

 

 线性回归的方程的一般形式为：y=wx+b

其中w表示为权重，b表示为偏重。我们的特征值x输入后，与权重w相乘，可能会有一点的偏重影响，最终得到目标值。

真实值和预测值肯定是会有误差的，我们想要努力缩小误差的话，可以使用损失函数来观察模型的误差大小，从而缩小误差。

 

减少损失有两种方式：最小二乘法中的回归方程和梯度下降法

 回归方程：

 

 其中X^T为转置矩阵，X^-1为逆矩阵

 

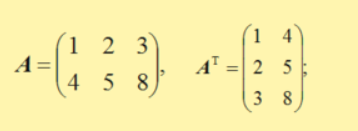
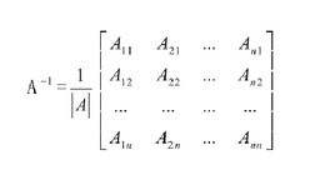
 梯度下降法：

 

 其中∂为学习速率，学习速率的取值取决于数据样本，可以多取一些值，从大到小，分别运行算法，看看迭代效果，如果损失函数在变小，说明取值有效，否则要增大步长。

 

2.思考线性回归算法可以用来做什么？（大家尽量不要写重复）

我觉得可以用来进行预测广告花费与产品销售额，当投入多少广告费时应该卖出多少产品。以及预测居民收入和居住面积之间的关系，看看当居民收入到一定水平时，可以住什么样的房子。

3.自主编写线性回归算法 ，数据可以自己造，或者从网上获取。（加分题）

这次我自己弄了点数据，研究一下学习时间和分数之间的关系。

数据如下图所示。

 

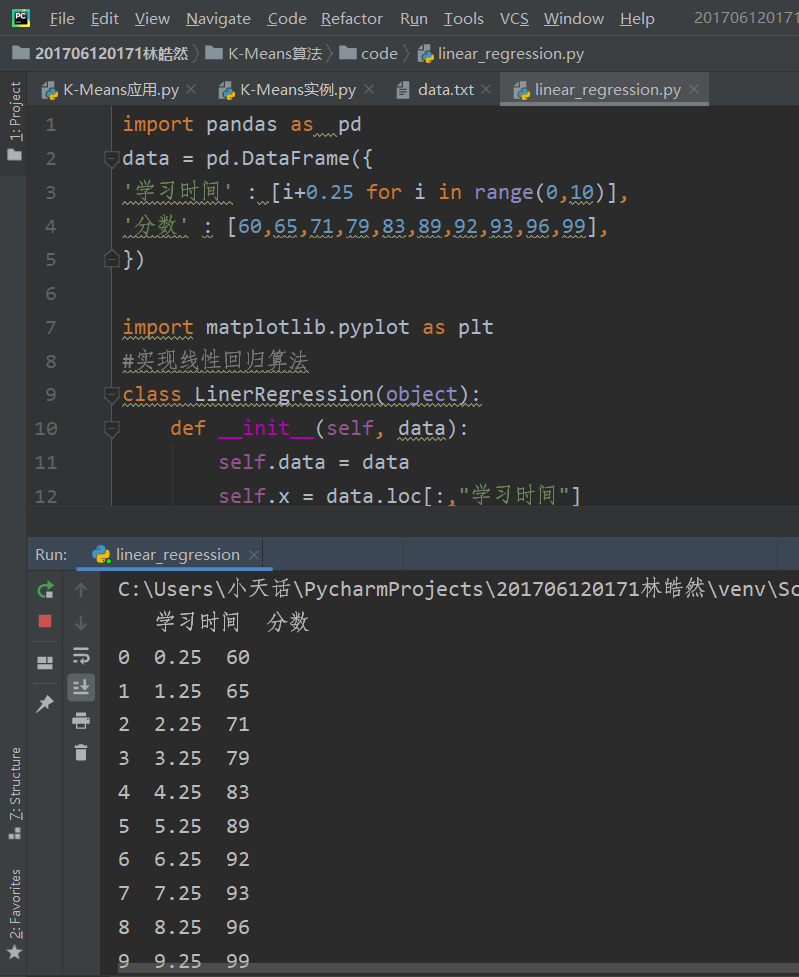
 自己参照一些资源和老师的课堂讲解，实现了线性回归算法。实现效果如下。

 

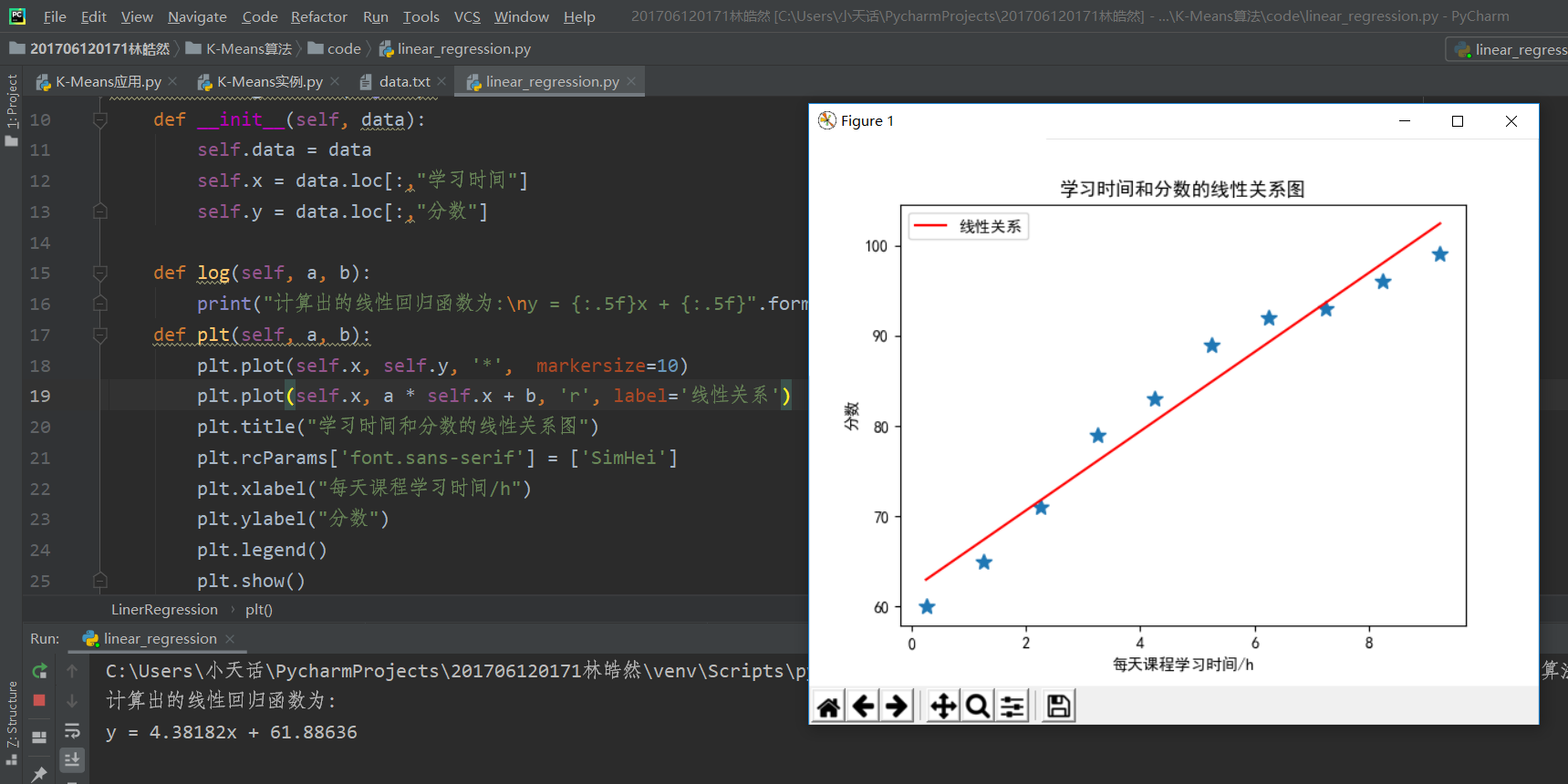
 实现代码：

import pandas as  pd
data = pd.DataFrame({
'学习时间' : [i+0.25 for i in range(0,10)],
'分数' : [60,65,71,79,83,89,92,93,96,99],
})

import matplotlib.pyplot as plt
#实现线性回归算法
class LinerRegression(object):
    def __init__(self, data):
        self.data = data
        self.x = data.loc[:,"学习时间"]
        self.y = data.loc[:,"分数"]

    def log(self, a, b):
        print("计算出的线性回归函数为:\ny = {:.5f}x + {:.5f}".format(a, b))#得出线性回归函数
    def plt(self, a, b):
        plt.plot(self.x, self.y, '*',  markersize=10)
        plt.plot(self.x, a * self.x + b, 'r', label='线性关系')#设置图例
        plt.title("学习时间和分数的线性关系图")
        plt.rcParams['font.sans-serif'] = ['SimHei']#解决中文显示问题
        plt.xlabel("每天课程学习时间/h")#设置x轴文字
        plt.ylabel("分数")#设置y轴文字
        plt.legend()
        plt.show()
    def least_square_method(self):#实现最小二乘法
        def calc_ab(x, y):
            sum_x, sum_y, sum_xy, sum_xx = 0, 0, 0, 0
            n = len(x)
            for i in range(0, n):
                sum_x += x[i]
                sum_y += y[i]
                sum_xy += x[i] * y[i]
                sum_xx += x[i]**2
            a = (sum_xy - (1/n) * (sum_x * sum_y)) / (sum_xx - (1/n) * sum_x**2)
            b = sum_y/n - a * sum_x/n
            return a, b
        a, b = calc_ab(self.x, self.y)
        self.log(a, b)
        self.plt(a, b)
print(data)#输出数据data
model = LinerRegression(data)#构建模型
model.least_square_method()#使用最小二乘法