第三次作业----K均值算法

1）. 扑克牌手动演练k均值聚类过程：>30张牌，3类

步骤一：首先将随机抽取的30张牌随机抽取3张牌。分别是4、8、Q。

 

 步骤二：将剩下的27张扑克牌根据与3张初始牌距离开始分类，分类效果如下图所示。

 

步骤三：通过求各类别平均值，求出新的类中心3、8、J。如图所示。

 步骤四：将其余27张牌重新根据与新类中心的距离进行分类，分类效果如下：

 

 步骤五：求出新类别的新类中心3、8、J，发现与上一次求出的新类中心一致，成功将30张牌分为3个类别。效果如图所示。

2）. *自主编写K-means算法 ，以鸢尾花花瓣长度数据做聚类，并用散点图显示。（加分题）

自己理解K-means算法后，使用鸢尾花花瓣长度数据进行实现，实现效果如下：

 

 

 

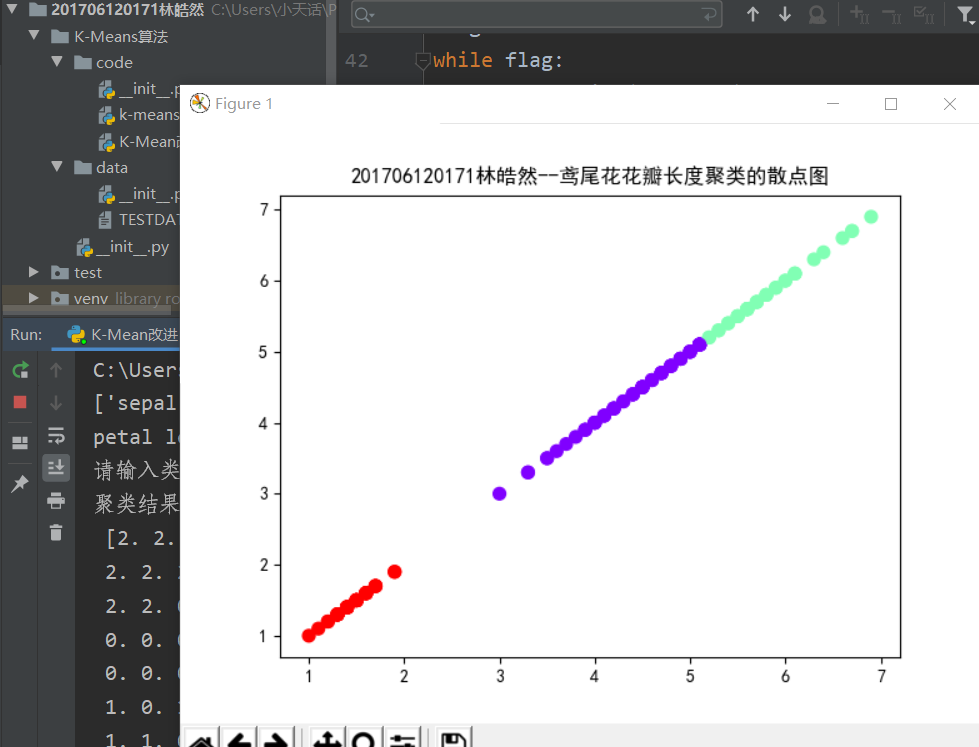
 实现代码如下：

import numpy as np
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
# 初始聚类中心数组
# 选择k个样本作为初始类中心
def firstCenter(x, k):
    # 选择后面k个样本作为初始类中心
    return x[-k:]
def minDist(kc, i):
    d = abs(kc - i) #获取距离最小值
    w = np.where(d == np.min(d))
    return w[0][0]
def classify(x, y, kc):
    for i in range(x.shape[0]):  # 进行分类
        y[i] = minDist(kc, x[i])
    return y
# 更新聚类中心：求每个类别中的均值作为该类别的聚类中心；
def mean(x, y, kc, k):
    li = list(kc)
    flag = False
    for i in range(k):
        m = np.where(y == i)
        n = np.mean(x[m])
        if li[i] != n:
            li[i] = n
            flag=True # 聚类中心发生变化
    return (np.array(li),flag)

iris = load_iris()
print(iris.feature_names)  # 特征名称
print("petal length为花瓣长度，即为第3列")
n = len(iris.data)   # 鸢尾花花瓣数据的长度
x = iris.data[:, 2]    # 获取花瓣长度
y = np.zeros(n)  # 初始化数组
k = input("请输入类中心K的取值:")
k = int(k)
kc = firstCenter(x, k)
flag = True
while flag:
    y = classify(x, y, kc)
    kc, flag = mean(x, y, kc, k)
print("聚类结果如下：\n", y)
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.scatter(x, x, c=y, s=50, cmap='rainbow')
plt.title("201706120171林皓然--鸢尾花花瓣长度聚类的散点图")
plt.show()

 

3）. 用sklearn.cluster.KMeans，鸢尾花花瓣长度数据做聚类，并用散点图显示.

 

 

 

 

 

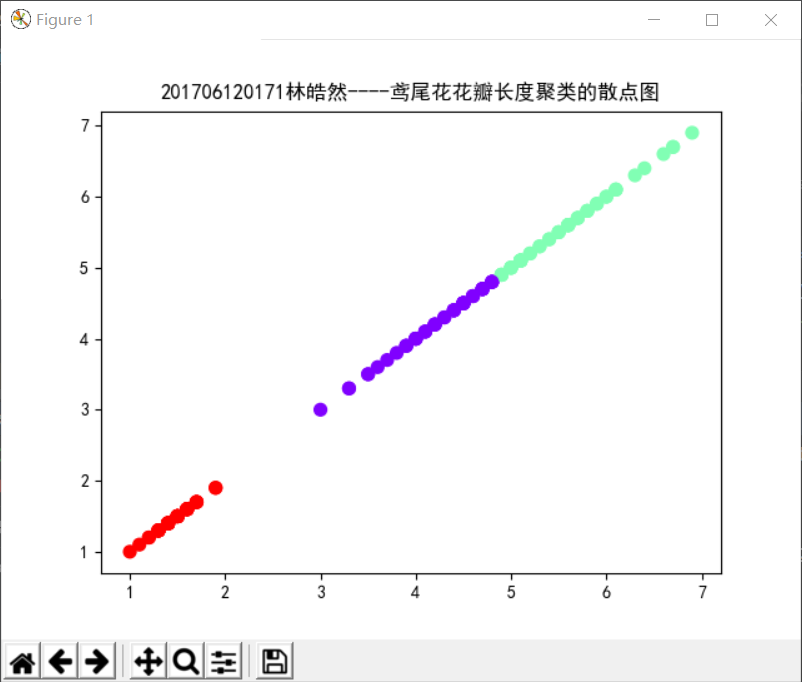
 实现代码如下：

from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

# 获取鸢尾花数据集
iris = load_iris()
x = iris.data[:, 2].reshape(-1, 1)  # 获取鸢尾花花瓣长度
k = input("请输入K的取值:")
k = int(k)
model = KMeans(k)  # 构建模型
model.fit(x)  # 训练
y = model.predict(x)  # 预测每个样本的聚类索引
print("鸢尾花花瓣数据预测结果：\n", y)
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.scatter(x[:, 0], x[:, 0], c=y, s=50, cmap='rainbow')
plt.title("201706120171林皓然----鸢尾花花瓣长度聚类的散点图")
plt.show()

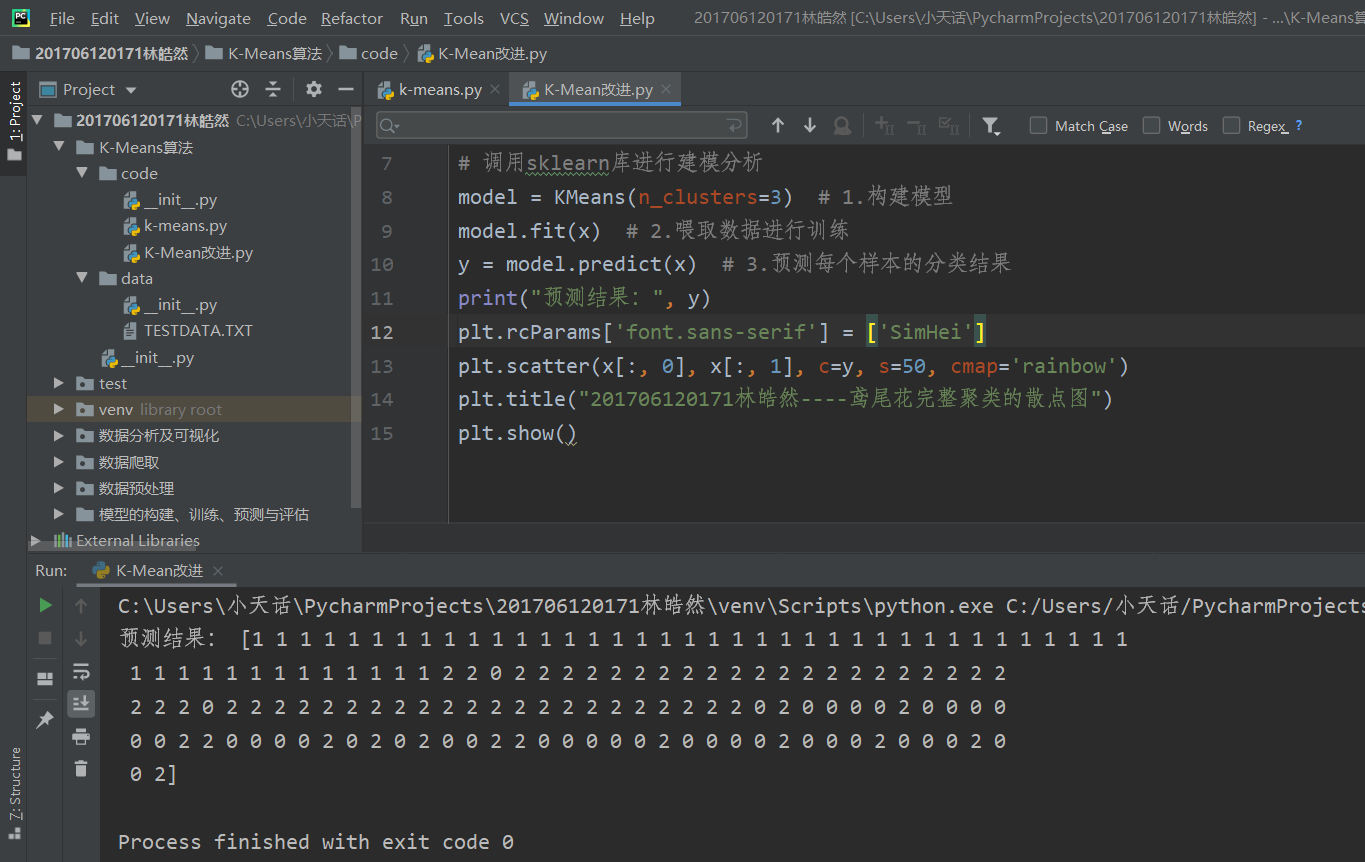
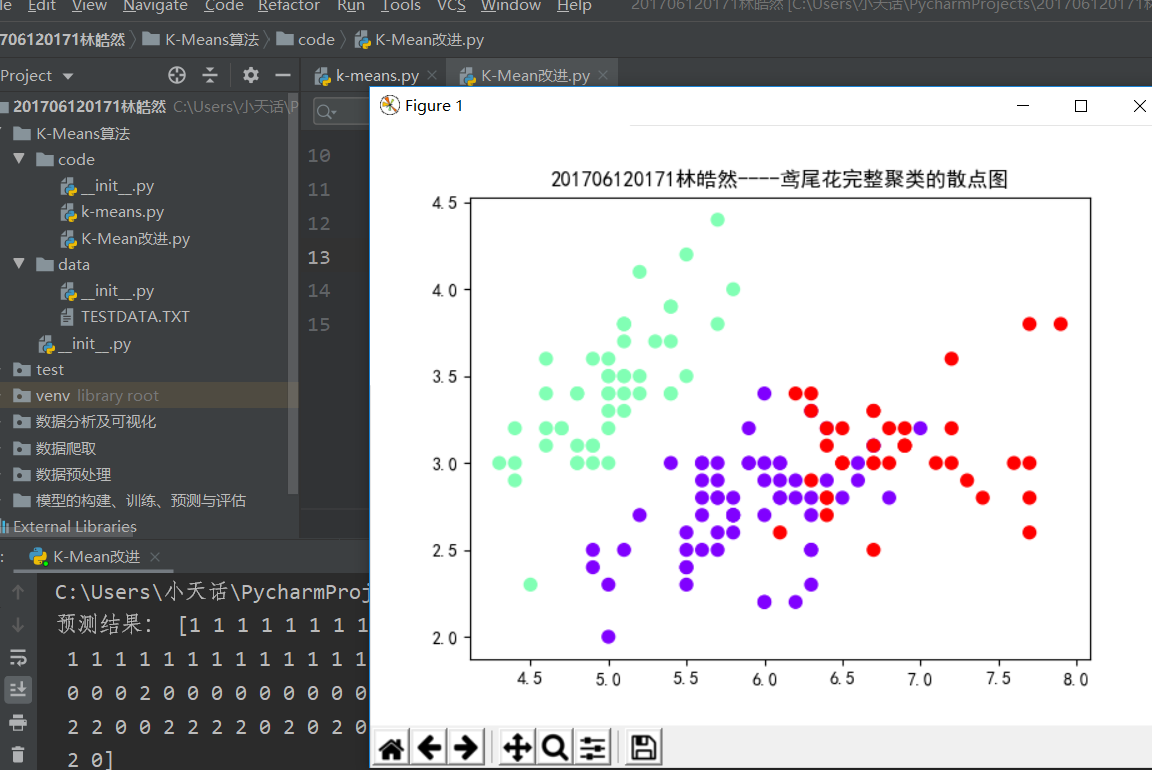
4）. 鸢尾花完整数据做聚类并用散点图显示.

调用sklearn.cluster.KMeans，鸢尾花完整数据做聚类分析，并用散点图显示，效果如下：

 

 

5）.想想k均值算法中以用来做什么？

我觉得可以对一些数据进行分类，可以快速区分同一品种的不同类型，比如种子的好坏程度，以及还可以分出一些比赛中那些队伍是种子队伍，哪些队伍是中等队伍和差劲队伍。