作业二----机器学习相关数学基础

1）贴上视频学习笔记，要求真实，不要抄袭，可以手写拍照。

 

概率作用于生活。但是其实概率和我们想象中的概率其实并不一样

 

 

 

举个例子：以前根据用户浏览记录进行商品推荐，但是在一些场景中通过一些随机性给用户带来惊喜感。

 

解题过程：

 

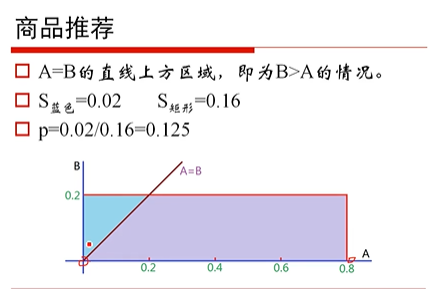
概率模型

作用：判断什么时候会堵车，自己的车什么时候可以加速减速。

 

基础概率公式

 

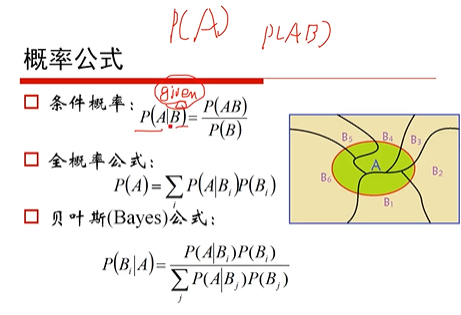
举个例子：

 

解题过程，利用公式得到概率为81.6%。

 

学习概率分布：

两点分布

 

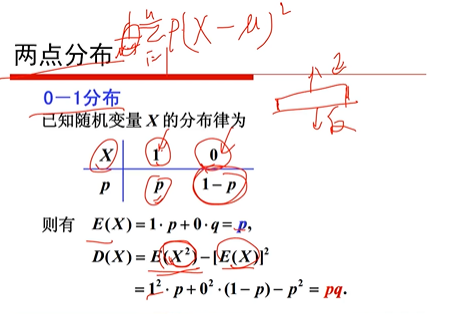
二项分布（伯努利分布）

 

泊松分布

 

 

泊松分布应用场景

 

均匀分布

 

指数分布

 

注意事项

 

正态分布

 

 

程序运行效果

 

 

 

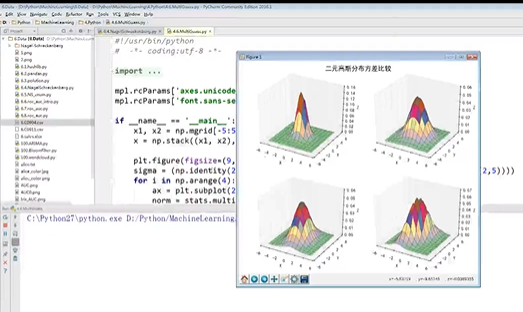
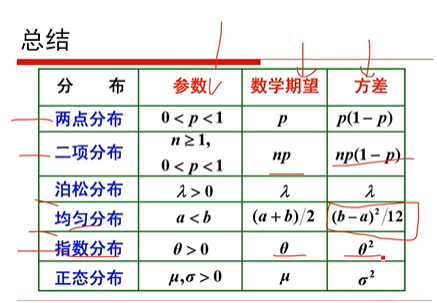
总结各个基本概率分布

 

 

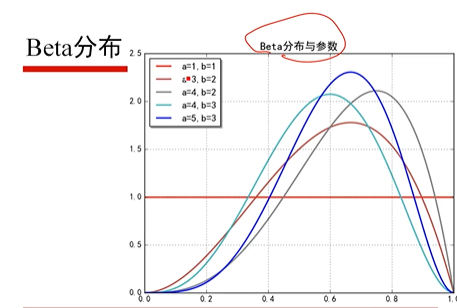
特殊的Beta分布（不同的模型之间的概率之间的联系）

 

 

 

 

指数族分布

 

高斯分布

 

事件独立性

 

期望的类别和性质

 

 

 

不相关和独立的区别和联系：

1. 独立一定不相关，不相关不一定独立（高斯过程里二者等价） 。

2. 对于均值为零的高斯随机变量，“独立”和“不相关”等价的。

举个例子

 

 

 

 

协方差

 

 

 

 

奇异值分解应用

 

线性代数

 

 

 

 

 

 

 

 

 

秩和线性方程组的解的关系

 

 

 

 

 

 

 

 

 

 

特征值和特征向量

 

 

 

 

 

2）用自己的话总结“梯度”，“梯度下降”和“贝叶斯定理”，可以word编辑，可做思维导图，可以手写拍照，要求言简意赅、排版整洁。

梯度：

有这么一个函数，他在某一个定点处沿不同的方向，每个方向的方向导数都是不相同的。我们根据在该顶点的方向导入在哪一个方向上达到最大值，那么就可以得出沿着这个梯度方向就可以让函数值增加的最快，相反的话就是函数值减少的最快。梯度和方向导数有着密切的联系，让我们可以得到函数在某一点处的方向导数在其梯度方向上达到最大值。

 

梯度下降：

就像是我们夜间在山上看不到路的时候又想尽快下山，我们就可能会想从山最陡峭的地方下去，我们可以寻找这个位置最陡峭的地方，然后朝着山的高度下降的地方走。我们如果不知道哪里是最陡峭的地方，我们就可以使用梯度下降法充当我们的导游，带领我们下山。

对应到函数中，就是找到给定点的梯度 ，然后朝着梯度相反的方向，就能让函数值下降的最快！

 

贝叶斯定理：

简单来说就是事件A在事件B(发生)的条件下的概率，与事件B在事件A的条件下的概率是不一样的

就拿最近的疫情说一下

100%的新冠病毒患者都有出现咳嗽，而某人有同样的咳嗽表现，绝对不代表该人有100%的概率感染新冠病毒，还需要考虑先验概率，假设感染新冠病毒后的咳嗽率是十万分之一，而全球有同样咳嗽的人有万分之一，则此人感染新冠病毒的概率只有十分之一，90%的可能没有感染到新冠病毒。