牛客多校训练营2022年（一）

Lexicographical Maximum

Eibwen is a newbie in Python.

You might know that when you input a number in the command line, your Python program will receive a string containing that number instead of a number that can be used to calculate. This is an interesting feature that a newbie might not know.

Eibwen wants to find the maximum of some given numbers, so he writes a program to sort the list of the numbers and print the last element in the sorted list. However, as a newbie, Eibwen doesn't know the feature. He actually sorts the list of number strings in lexicographical order and prints the last string in the list.

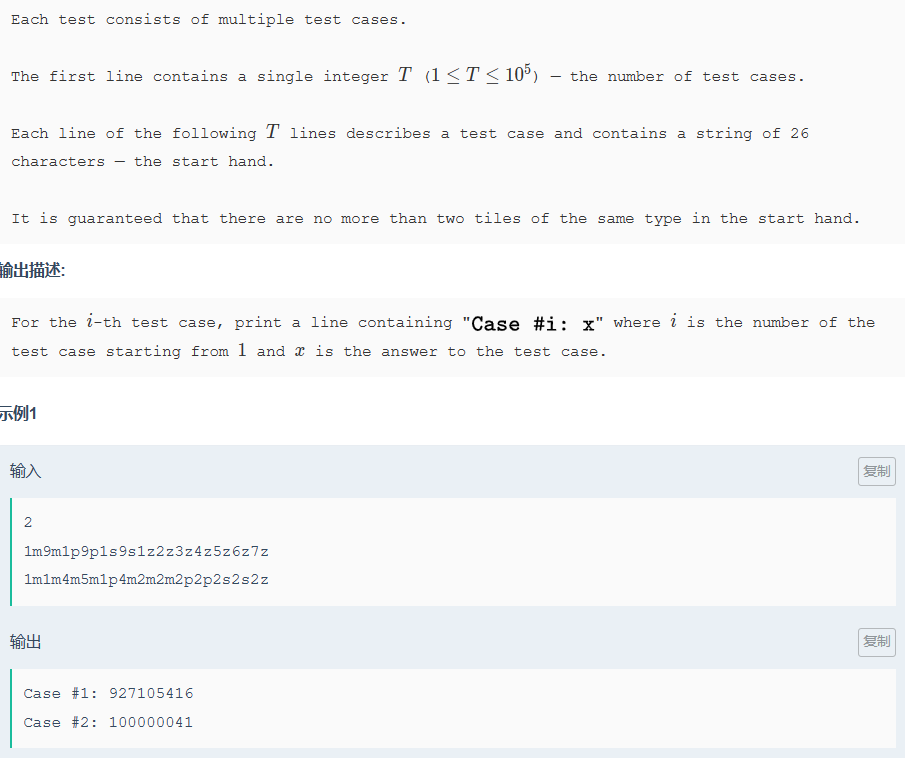
Now Eibwen runs his program, inputs all the integers from 1 to n, and finds his program really slow. Could you help

him find out the expected output of his program?

Input

The only line contains an integer n — the size of Eibwen's input.

Output
Print the expected output of Eibwen's program in a single line, which actually is the lexicographically maximum from 1 to n.

input	output
616	99

 

做法：贪心，如果n这个数的前n-1位都是9，则直接输出这个数，否则就输出n-1个数字9。

#include <iostream>
#define int long long 
const int N=1000010;


using namespace std;
signed main()
{
    string s;
    cin>>s;
    int cnt = 0;
    int l = s.size();
    for(int i = 0;i < l - 1;i ++ )
    {
        if(s[i] == '9')
        {
            cnt ++ ;
            
        }
        
    }
    if(cnt == l - 1)
    {
        for(int i = 0;i < l ;i ++ )
        {
            cout<<s[i];
        }
    }
    else
    {
        for(int i = 0;i < l - 1;i ++ )
        {
            cout<<"9";
        }
    }
    return 0;
    
}

 Villages: Landlines

 

 

 

 

做法：我们将所有坐标及半径看成n个坐标轴上的区间，假设发电站的范围内有无数个变电塔，我们就只需要计算从左到右的区间中不连通区域的长度，这个长度就是所要求的导线长度。在输入时，我们将坐标x与半径r转化为区间的左右端点[x-r.x+r]，然后对所有区间进行排序,再扫一遍找到区间中不连通区域的长度即可。

#include <bits/stdc++.h>
using namespace std;
const int N=1000010;


struct node 
{
    int l, r;
}a[N];
bool cmp(node a,node b)
{
    if(a.l == b.l)
    {
        return a.r < b.r;
    }
    return a.l < b.l;
}
signed main()
{
    int n;
    cin>>n;
    for(int i = 1 ; i <= n ; i ++ )
    {
        int x, r;
        cin>>x>>r;
        a[i].l = x - r;
        a[i].r = x + r;
    }
    sort(a + 1, a + 1 + n, cmp);
    int ans = 0;
    int right = a[1].r;
    for(int i = 2; i <= n; i ++)
    {
        if(a[i].l <= right)
        {
            right = max(a[i].r, right);
        }
        else
        {
            ans += a[i].l - right;
            right = a[i].r;
        }
    }
    cout << ans;
    return 0;
    
}

Mocha and Railgun

 

 

 

 

 

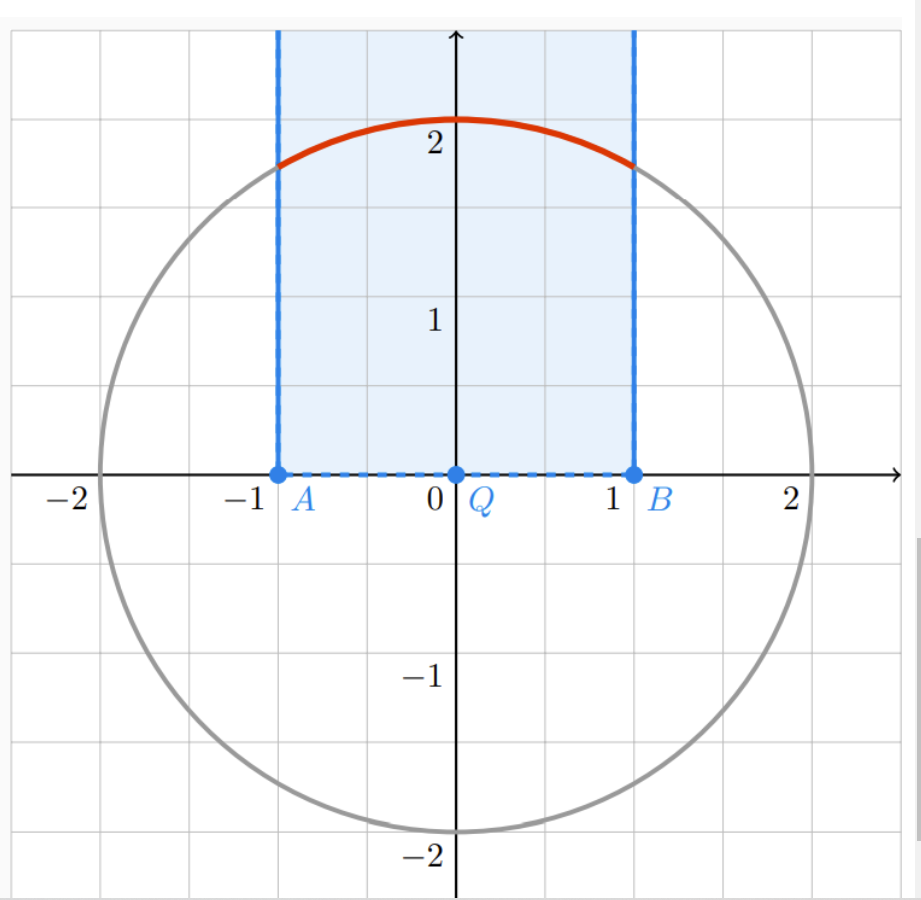
#include <bits/stdc++.h>
#define int long long 
const int N=10000010;


const double pi = acos(-1);
using namespace std;
signed main()
{
    int t;
    cin>>t;
    while(t--)
    {
        double r;
        
        double x, y, d;        
        cin>>r>>x>>y>>d;
        
        double dis = sqrt(x * x + y * y);
        double a1 = acos((d - dis) / r);
        double a2 = acos((d + dis) / r);
        double a3 = pi - a1 - a2;
        

        printf("%.12lf\n",a3 * r);
    }
    return 0;
    
}

   Chiitoitsu （概率  dp  绝对是一道不错的题）

 

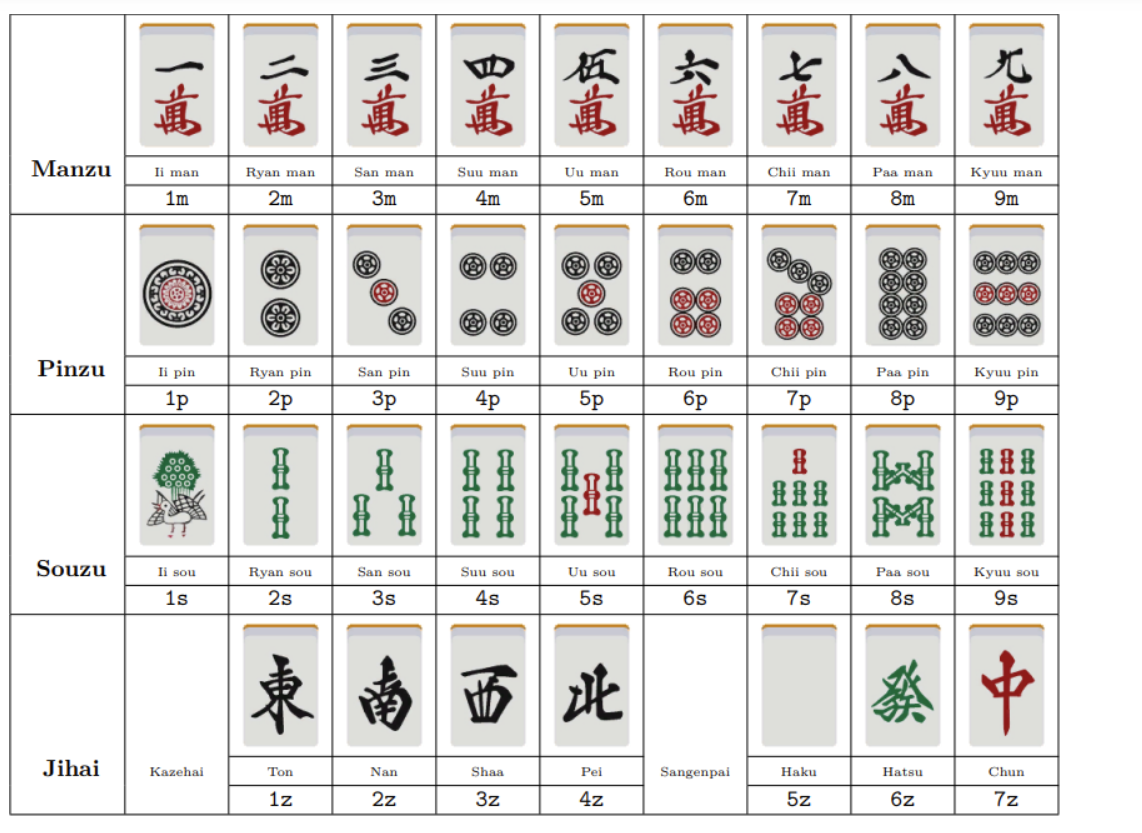
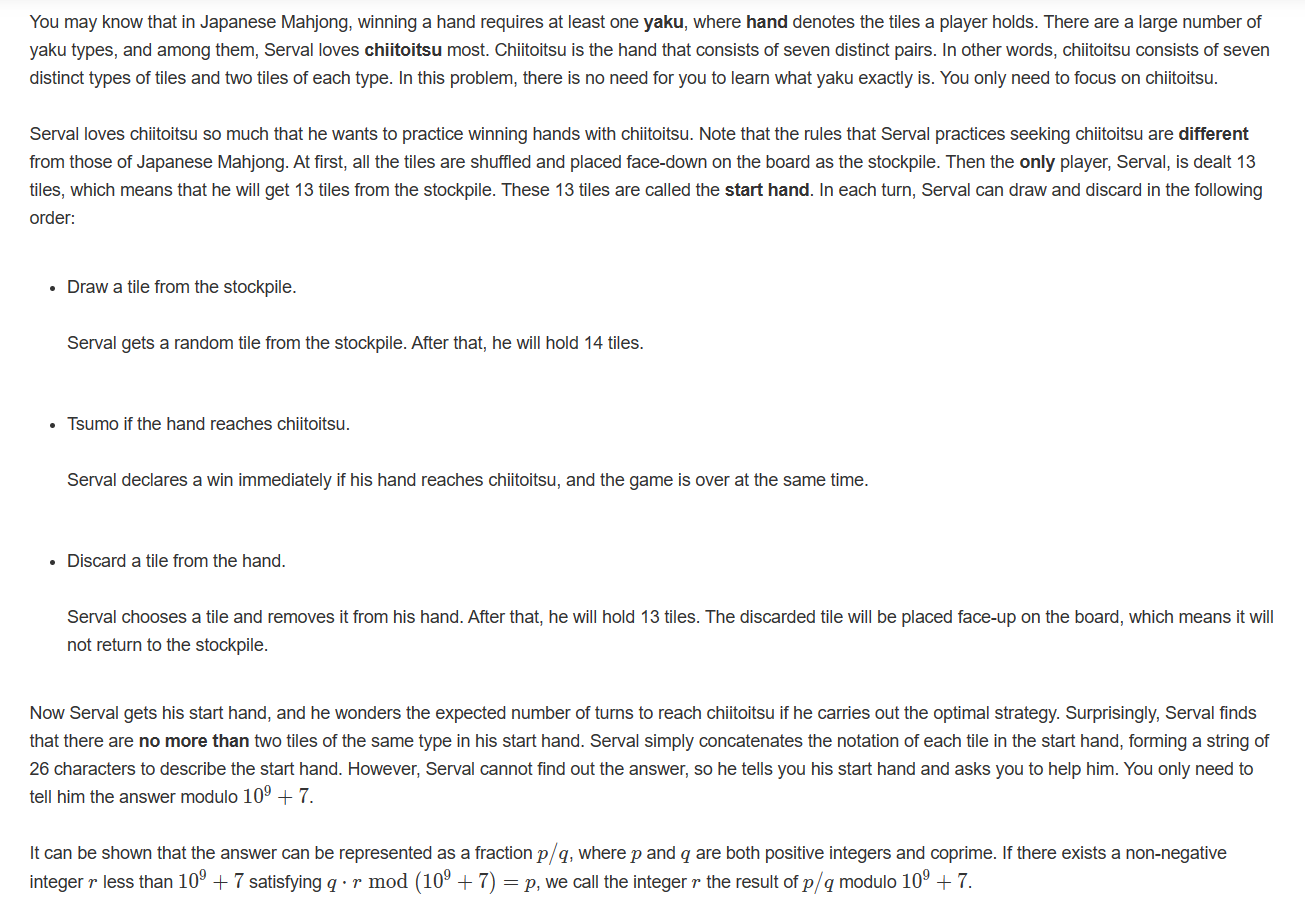
#include <bits/stdc++.h>
#define int long long 
using namespace std;


const int N=10000010;
map<string,int> mp;

int dp[10][150];
const int mod = 1e9 + 7;
int qmi(int a,int b)
{
    int res = 1;
    while(b)
    {
        if(b & 1)
        {
            res = res * a % mod;
        }
        a = a * a % mod;
        b >>= 1;
    }
    return res;
    
}
void core()
{
    for(int i = 6;i >= 0;i -- )
    {
        int good = (13 - i * 2) * 3;
        for(int j = good;j <= 123;j ++ )
        {
            int bad = j - good;
            int fact = qmi(j, mod - 2);
            dp[i][j] = (dp[i + 1][j - 1] * good % mod *fact % mod + dp[i][j - 1] * bad % mod * fact % mod + 1) % mod;
        }
    }
}
signed main()
{
    core();
    
    int t;
    cin>>t;
    for(int i=1;i<=t;i++)
    {
        string s;
        cin>>s;
        mp.clear();
        int sum = 0;
        string ss;
        for(int i = 0;i < s.size();i += 2 )
        {
            ss = "";
            ss += s[i];
            ss += s[i + 1];
            mp[ss] ++;
            if(mp[ss] > 1)
            {
                sum ++;
            }
        }
        printf("Case #%lld: %lld\n",i,dp[sum][123]);
        
    }
}