记录牛客网分糖果问题

我在学习 java ，因此编程都是用 java 来做题的

在记录糖果数时，我想用逆向指针添加递减的糖果数，因此还需要判断逆向最高点是否需要取代正向最高点

排行中第一位使用正向指针代替逆向指针，并且巧妙地处理最高点，在此记录

描述

　　一群孩子做游戏，现在请你根据游戏得分来发糖果，要求如下：

　　1. 每个孩子不管得分多少，起码分到一个糖果。

　　2. 任意两个相邻的孩子之间，得分较多的孩子必须拿多一些糖果。(若相同则无此限制)

　　给定一个数组 arr 代表得分数组，请返回最少需要多少糖果。

　　要求: 时间复杂度为O(n) 空间复杂度为 O(n)

　　数据范围： 1≤n≤100000 ，1≤ai​≤1000

 

 

使用新建数组 candy[] 保存糖果数，分析题目，得出以下几点结论

　　1，数组中最小值为1

　　2，当前索引在 arr[] 中大于左边或右边值时， candy[] 中的糖果数也应该大于对应边的值

　　3，极大值，若 arr[] 中的值大于两边值，则 candy[] 中值也该大于两边值。极小值，若 arr[] 中的值小于两边值，则 candy[] 中值应该为1

　　4，得分相同的相邻孩子不需要拿相同数量的糖果（这点是在答案出错时发现的，我觉得这不公平，但按题来讲这样才公平）

 

　　新建数组 candy[] 用来保存与 arr[] 对应糖果数

　　我希望一次遍历就可以在数组中填充全部值，因此遍历指针 i 无法回溯

　　另起 int n 用来保存返回时的极限，当递减到下一项大于等于自身时，记当前项为 m ，则指针从 m 回溯到 n ，从 1 开始赋值

　　回到最高点 n 时，自然需要判断此时值是否需要覆盖原先的最大值，否则无法满足题目第 1 点，得分较多的孩子必须比两边孩子大

　　因为需要比较左或右，因此遍历时首尾需要放弃一端，否则会产生越界错误，因为无法一次确定首位值，因此我选择在最后分情况补上尾位

 

　　高手来了，与其记录回溯点，顺序为 n 到 1 ，不如直接记录 1 到 n ，最后计算总数是一样的

　　原本应该回到5的，改个顺序不影响最终结果

　　并且原先不好计算的首位值，这样就可以计算了，相当于将原先首位值移到后面去，计算时将首位当做 1 

　　再大的首位值也能用后面的1代替

 

 

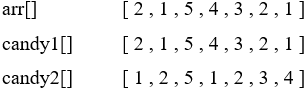
　　那么怎么确保极大值正确呢？

　　当增到极大值时直接跳过，反正要修改极大值，原来的极大值也需要保留，原本用6代替5，现在直接把6放后面

 

 

 　　如此一来记录的糖果数与分数无法对应，但题目只需要最后的糖果值，不影响最终结果

　　下面是代码，我还是想用数据保存糖果值，但实际上利用到的只有极大值对应的索引，只保存极大值也是可以的

我的代码

    /**
     * pick candy
     * @param arr int整型一维数组 the array
     * @return int整型
     */
     //若相同则无此限制，相邻分数相同的孩子糖果数能不同？？？
     //我以为相邻孩子糖果数应该相同
    public int candy (int[] arr) {

        int length = arr.length;    //长度
        int[] candy = new int[length];  //保存数组
        int n = -1; //now，可能第一个就是极大值，没法用0
        int c = 1;  //缓存递增值cache
        int r = 0;  //result
        int i;  //循环结束时i刚好为length-1，所以拿外面来
        for ( i = 0 ; i < length - 1; i++) {
            if (n == -1) {
                //正在递增时，找极大值
                candy[i] = c;
                r = r + c;
                //提前为下一增量增加糖果值
                if (arr[i] < arr[i + 1]) {
                    c++;
                //下一值变小，保存坐标
                } else if (arr[i] > arr[i + 1]) {
                    n = i;
                }else{
                    c=1;
                }
            } else {
                //n有值说明现在再找极小值
                if (arr[i] <= arr[i + 1]) {
                    c = 1;
                    for (int a = 0; a < i - n; a++) {
                        candy[i - a] = c;
                        r = r + c;
                        c++;
                    }
                    //检测极大值是否需要更换
                    if (c > candy[n]) {
                        r = r - candy[n] + c;
                        candy[n] = c;
                    }
                    n = -1;
                    //下一项比自身大，则认为下一项为2，否则为1
                    if(arr[i] == arr[i + 1]){c = 1;}else{c=2;}
                    
                }
                //未到极小值，不需要任何操作
            }
        }
        //根据n是否有值判断是否在找极小值
        if (n == -1) {
            //最后一项是极大值
            candy[i] = c;
            r = r + c;
        } else {
            //最后一项是极小值
            c = 1;
            for (int a = 0; a < i - n; a++) {
                candy[i - a] = c;
                r = r + c;
                c++;
            }
            //检测极大值是否需要更换
            if (c > candy[n]) {
                r = r - candy[n] + c;
                candy[n] = c;
            }
        }
        return r;
    }

高手代码

    public static int candy(int[] nums) {
        //我忘记考虑输入为空的情况了
        if (nums == null || nums.length == 0) return 0;
        int n = nums.length;    //记录长度
        int pre = 1;    //糖果值
        int ans = 1;    //返回值
        //Inlen记录最高峰，Delen将回溯指针正向递增
        int DeLen = 0, InLen = 1;
        //默认 0 位为 1
        for (int i = 1; i < n; i++) {
            if (nums[i] >= nums[i - 1]) {
                //相等时从1计算，无论接下来是增还是减
                if (nums[i] == nums[i - 1]) pre = 1;
                else pre++;
                ans += pre;
                InLen = pre;
                DeLen = 0;
            } else {
                DeLen++;
                //跳过极大值
                if (DeLen == InLen) DeLen++;
                ans += DeLen;
                pre = 1;
            }
        }
        return ans;
    }