代码随想录算法 - 二叉树4

题目1 654. 最大二叉树

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

1. 创建一个根节点，其值为 nums 中的最大值。
2. 递归地在最大值 左边 的 子数组前缀上 构建左子树。
3. 递归地在最大值 右边 的 子数组后缀上 构建右子树。

返回 nums 构建的 *最大二叉树* 。

示例 1：

输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：
- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
    - [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
        - 空数组，无子节点。
        - [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
            - 空数组，无子节点。
            - 只有一个元素，所以子节点是一个值为 1 的节点。
    - [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
        - 只有一个元素，所以子节点是一个值为 0 的节点。
        - 空数组，无子节点。

示例 2：

输入：nums = [3,2,1]
输出：[3,null,2,null,1]

提示：

• 1 <= nums.length <= 1000
• 0 <= nums[i] <= 1000
• nums 中的所有整数 互不相同

思路

递归法

这道题的出题人还挺好的，把解法都写在题目里了，按照给出的方法递归创建递归树就行了

代码

class Solution {
public:
    TreeNode* consturctTree(vector<int>& nums, int left, int right)
    {
        int index = left;
        for(int i = left; i <= right; i++)
        {
            if(nums[i] > nums[index])
                index = i;
        }
        TreeNode* curNode = new TreeNode(nums[index]);
        if(left <= index - 1)
            curNode->left = consturctTree(nums, left, index - 1);
        if(index + 1 <= right)
            curNode->right = consturctTree(nums, index + 1, right);
        return curNode;
    }
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        return consturctTree(nums, 0, nums.size() - 1);
    }
};

题目2 617. 合并二叉树

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

示例 1：

输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]

示例 2：

输入：root1 = [1], root2 = [1,2]
输出：[2,2]

提示：

• 两棵树中的节点数目在范围 [0, 2000] 内
• -104 <= Node.val <= 104

思路

递归法

进入递归函数时注意root1子树和root2子树的4种状态就能做了，1.两个子树全为空，则返回nullptr，2.root1子树为空，3.root2子树为空，4.两个子树都不为空，则进行当前节点的合并与处理双child节点。

代码

class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        if(root1 == nullptr)
            return root2;
        if(root2 == nullptr)
            return root1;
        if(root1 == nullptr && root2 == nullptr)
            return nullptr;
        root1->val += root2->val;
        root1->left = mergeTrees(root1->left, root2->left);
        root1->right = mergeTrees(root1->right, root2->right);
        return root1;
    }
};

题目3 700. 二叉搜索树中的搜索

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null 。

示例 1:

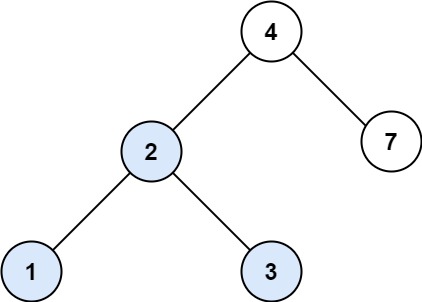
输入：root = [4,2,7,1,3], val = 2
输出：[2,1,3]

示例 2:

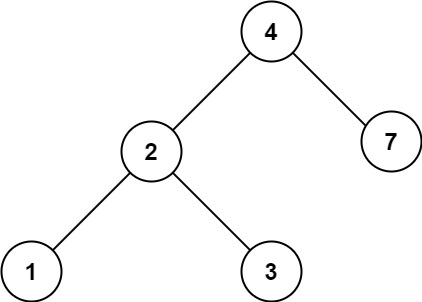
输入：root = [4,2,7,1,3], val = 5
输出：[]

提示：

• 树中节点数在 [1, 5000] 范围内
• 1 <= Node.val <= 107
• root 是二叉搜索树
• 1 <= val <= 107

思路

基础题，考察二叉搜索树的查询操作，有递归法和迭代法。

递归法

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if(root == nullptr)
            return nullptr;
        if(root->val == val)
            return root;
        return root->val > val ? searchBST(root->left, val) : searchBST(root->right, val);
    }
};

迭代法

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if(!root->left && !root->right)
            return root->val == val ? root : nullptr;
        TreeNode* curNode = root;
        while(curNode)
        {
            if(curNode->val == val)
                return curNode;
            curNode = curNode->val > val ? curNode->left : curNode->right;
        }
        return curNode;
    }
};

题目4 98. 验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左

  子树

  只包含

  小于

  当前节点的数。

• 节点的右子树只包含 大于 当前节点的数。

• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

输入：root = [2,1,3]
输出：true

示例 2：

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

• 树中节点数目范围在[1, 104] 内
• -231 <= Node.val <= 231 - 1

思路

递归法

这道题主要是注意比当前节点大和比当前节点小的节点的位置是否正确，这个是陷阱，解决了这个就AC了。

代码

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        if(!root->left && !root->right)
            return true;
        bool lft = true, rht = true;
        TreeNode * tmpNode = nullptr;
        if(root->left)
        {
            lft = root->left->val < root->val && isValidBST(root->left);
            tmpNode = root->left;
            while(tmpNode->right)
            {
                tmpNode = tmpNode->right;
            }
            lft = lft && tmpNode->val < root->val;
        }
        if(root->right)
        {
            rht = root->right->val > root->val && isValidBST(root->right);
            tmpNode = root->right;
            while(tmpNode->left)
            {
                tmpNode = tmpNode->left;
            }
            rht = rht && tmpNode->val > root->val;
        }
        return lft && rht;
    }
};