代码随想录算法 - 二叉树2
题目1 110. 平衡二叉树
给定一个二叉树,判断它是否是
平衡二叉树
示例 1:

输入:root = [3,9,20,null,null,15,7]
输出:true
示例 2:

输入:root = [1,2,2,3,3,null,null,4,4]
输出:false
示例 3:
输入:root = []
输出:true
思路
这道题只要循环的去比较子树的高度就可以了,可以用递归法和迭代法做。
递归法
class Solution {
public:
int depth(TreeNode* root)
{
if(!root)
{
return 0;
}
return max(depth(root->left), depth(root->right)) + 1;
}
bool isAvlTree(TreeNode* root)
{
if(!root)
{
return true;
}
int val = abs(depth(root->left) - depth(root->right));
return 0 <= val && val < 2 && isAvlTree(root->left) && isAvlTree(root->right);
}
bool isBalanced(TreeNode* root) {
if(!root)
{
return true;
}
return isAvlTree(root);
}
};
迭代法
这道题用迭代法做要使用辅助栈和队列来计算深度和保存子节点。(也可以使用栈+后序遍历来计算深度。)
代码
class Solution {
public:
int depth(TreeNode* root)
{
if(!root)
{
return 0;
}
queue<TreeNode*> nodeStack;
nodeStack.push(root);
int depth = 0;
while(!nodeStack.empty())
{
int num = nodeStack.size();
for(int i = 0; i < num; i++)
{
TreeNode* cur = nodeStack.front();
nodeStack.pop();
if(cur->left)
nodeStack.push(cur->left);
if(cur->right)
nodeStack.push(cur->right);
}
depth++;
}
cout << endl;
return depth;
}
bool isBalanced(TreeNode* root) {
if(!root)
{
return true;
}
stack<TreeNode*> nodeStack;
nodeStack.push(root);
while(!nodeStack.empty())
{
int num = nodeStack.size();
for(int i = 0; i < num; i++)
{
TreeNode* cur = nodeStack.top();
nodeStack.pop();
if(abs(depth(cur->left) - depth(cur->right)) > 1)
{
return false;
}
if(cur->left)
nodeStack.push(cur->left);
if(cur->right)
nodeStack.push(cur->right);
}
}
return true;
}
};
题目2 257. 二叉树的所有路径
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
示例 1:
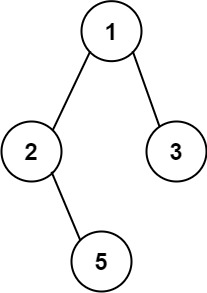
输入:root = [1,2,3,null,5]
输出:["1->2->5","1->3"]
示例 2:
输入:root = [1]
输出:["1"]
提示:
- 树中节点的数目在范围
[1, 100]内 -100 <= Node.val <= 100
思路
递归法
使用递归法,每次将一个非空节点加入string对象中,当且仅当该节点无孩子节点时将string保存到vector对象中;当有孩子时递归调用孩子的处理函数。
代码
class Solution {
public:
void getPath(TreeNode* root, vector<string> &vec, string str)
{
str += "->" + to_string(root->val);
if(!root->left && !root->right)
{
vec.push_back(move(tmpstr));
return;
}
if(root->left)
{
getPath(root->left, vec, str);
}
if(root->right)
{
getPath(root->right, vec, str);
}
}
vector<string> binaryTreePaths(TreeNode* root) {
if(!root->left && !root->right)
{
return vector<string>(1, to_string(root->val));
}
vector<string> result;
if(root->left)
getPath(root->left, result, to_string(root->val));
if(root->right)
getPath(root->right, result, to_string(root->val));
return result;
}
};
迭代法
mmp,写着写着头晕了,随想录里用两个辅助栈做起来确实简单。我这道题用的后序遍历以及一个辅助栈stack和一个辅助string来做的,除了根节点要单独处理外,要注意的是其他节点可能有两种可能,分别是叶子节点和非叶子节点。碰到叶子节点直接出栈并保存string到vector对象中;碰到非叶子节点有三种可能,分别是才入栈的节点,将左孩子加入栈的节点,将左右孩子都加入栈的节点。才入栈的节点由一个TreeNode*对象表示,左孩子入栈过的节点用一个TreeNode*和一个nullptr表示,左右孩子都处理过了用一个TreeNode*和两个nullptr表示。
代码
class Solution {
public:
int length(int & value)
{
int length = 0;
if(value < 0)
length++;
while(value)
{
length++;
value /= 10;
}
return move(length);
}
vector<string> binaryTreePaths(TreeNode* root) {
//根节点的双child节点为空则直接返回
if(!root->left && !root->right)
{
return vector<string>(1, to_string(root->val));
}
vector<string> result;
//根节点单独处理一下
string str(to_string(root->val));
stack<TreeNode*> nodeStack;
if(root->right)
nodeStack.push(root->right);
if(root->left)
nodeStack.push(root->left);
int size;
while(!nodeStack.empty())
{
TreeNode* curNode = nodeStack.top();
//curNode为空则说明curNode的左child节点已经加过nodeStack并处理过了
if(curNode == nullptr)
{
nodeStack.pop();
curNode = nodeStack.top();
//curNode还为空则说明curNode的右节点已经加过并且处理过了
if(curNode == nullptr)
{
//因为非叶子节点要压入三次栈,因此要出三次
nodeStack.pop();
size = length(nodeStack.top()->val);
nodeStack.pop();
str.erase(str.size() - (2 + size), 2 + size);
}
//未处理过的curNode
else
{
//压入两次nullptr表示该非叶子节点已经成功压入左孩子和右孩子
nodeStack.push(nullptr);
nodeStack.push(nullptr);
if(curNode->right)
{
nodeStack.push(curNode->right);
}
}
}
else
{
str += "->" + to_string(curNode->val);
//若节点没有双child则为叶子节点,添加到result中
if(!curNode->left && !curNode->right)
{
result.push_back(str);
size = length(curNode->val);
str.erase(str.size() - (2 + size), 2 + size);
nodeStack.pop();
}
//非叶子节点则继续压入nullptr用于判断该节点是否处理过
else
{
nodeStack.push(nullptr);
}
if(curNode->left)
{
nodeStack.push(curNode->left);
}
}
}
return move(result);
}
};
题目4 404. 左叶子之和
给定二叉树的根节点 root ,返回所有左叶子之和。
示例 1:
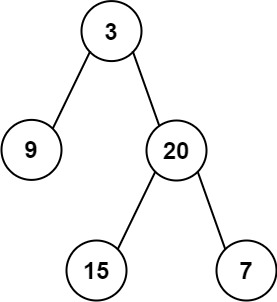
输入: root = [3,9,20,null,null,15,7]
输出: 24
解释: 在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24
示例 2:
输入: root = [1]
输出: 0
思路
递归
主要是每个节点是否为左节点这个状态要记录,记录好了就正常递归做就行了,终止边界是空节点或者叶子节点。
代码
class Solution {
public:
int lftValueSum(TreeNode* root, bool isLeft)
{
if(root == nullptr)
{
return 0;
}
if(!root->left && !root->right )
{
return isLeft ? root->val : 0;
}
return lftValueSum(root->left, true) + lftValueSum(root->right, false);
}
int sumOfLeftLeaves(TreeNode* root) {
return lftValueSum(root, false);
}
};
迭代法
代码随想录里的迭代法是用parent节点来判断左孩子是否为左叶子节点,我使用的是左叶子节点直接判断的方法来解决这道题。在入栈时对左孩子入栈两次,则左孩子节点就被标记了,左叶子节点就多了个双child节点为nullptr的条件。知道了这些就好做了。
代码
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
int sum = 0;
stack<TreeNode*> nodeStack;
nodeStack.push(root);
while(!nodeStack.empty())
{
TreeNode* curNode = nodeStack.top();
nodeStack.pop();
if(curNode == nullptr)
{
curNode = nodeStack.top();
nodeStack.pop();
if(!curNode->left && !curNode->right)
{
sum += curNode->val;
continue;
}
}
if(curNode->left)
{
nodeStack.push(curNode->left);
nodeStack.push(nullptr);
}
if(curNode->right)
{
nodeStack.push(curNode->right);
}
}
return sum;
}
};
题目4 222. 完全二叉树的节点个数
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
示例 1:

输入:root = [1,2,3,4,5,6]
输出:6
示例 2:
输入:root = []
输出:0
示例 3:
输入:root = [1]
输出:1
提示:
- 树中节点的数目范围是
[0, 5 * 104] 0 <= Node.val <= 5 * 104- 题目数据保证输入的树是 完全二叉树
进阶:遍历树来统计节点是一种时间复杂度为 O(n) 的简单解决方案。你可以设计一个更快的算法吗?
思路
递归
前中后续递归都可以遍历所有的节点
代码
class Solution {
public:
int countNodes(TreeNode* root) {
if(root == nullptr)
{
return 0;
}
return 1 + countNodes(root->left) + countNodes(root->right);
}
};
迭代法
用前中后层序都可以做
代码
class Solution {
public:
int countNodes(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
int result = 0;
while (!que.empty()) {
int size = que.size();
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
result++; // 记录节点数量
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
}
return result;
}
};
公式法(可递归可迭代)*
我硬套的公式,写的很糟糕。代码随想录里的公式法很有用,运用了分而治之的思想,每个完全二叉树可拆分为满二叉树+完全二叉树。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号