数组4：长度最小的子数组（209）

本题如下：（链接：https://leetcode.cn/problems/minimum-size-subarray-sum/）

题目：给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。

示例：输入：s = 7, nums = [2,3,1,2,4,3] 输出：2 解释：子数组 [4,3] 是该条件下的长度最小的子数组。

 

1.暴力解法：这道题目暴力解法很容易想到，即使用两个for循环，然后不断的寻找符合条件的子序列，时间复杂度明显是O(n^2)。

代码如下：

class Solution {
public:
    int minSubArrayLen(int s, vector<int>& nums) {
        int result = INT32_MAX; // 最终的结果
        int sum = 0; // 子序列的数值之和
        int subLength = 0; // 子序列的长度
        for (int i = 0; i < nums.size(); i++) { // 设置子序列起点为i
            sum = 0;
            for (int j = i; j < nums.size(); j++) { // 设置子序列终止位置为j
                sum += nums[j];
                if (sum >= s) { // 一旦发现子序列和超过了s，更新result
                    subLength = j - i + 1; // 取子序列的长度
                    result = result < subLength ? result : subLength;
                    break; // 因为我们是找符合条件最短的子序列，所以一旦符合条件就break
                }
            }
        }
        // 如果result没有被赋值的话，就返回0，说明没有符合条件的子序列
        return result == INT32_MAX ? 0 : result;
    }
};

可以发现，该方法的时间复杂度为：O(n^2)，空间复杂度为：O(1)。但在力扣中使用这种解法已经超时了。于是下面我们介绍其他更优的方法。

 

 

 

 

2.滑动窗口-----------数组操作中的另一个重要的方法

所谓滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果。

在暴力解法中，是一个for循环滑动窗口的起始位置，一个for循环为滑动窗口的终止位置，用两个for循环完成了一个不断搜索区间的过程。

而在滑动窗口中，首先要思考，如果用一个for循环，那么应该表示 滑动窗口的起始位置，还是终止位置。

如果只用一个for循环来表示 滑动窗口的起始位置，那么如何遍历剩下的终止位置？

此时难免再次陷入 暴力解法的怪圈。所以，只用一个for循环，那么这个循环的索引，一定是表示滑动窗口的终止位置。

那么问题来了， 滑动窗口的起始位置如何移动呢？

这里以题目中的示例来举例，s=7， 数组是 2，3，1，2，4，3。

那么在本题中实现滑动窗口，主要确定如下三点：（1）窗口内是什么？（2）如何移动窗口的起始位置？（3）如何移动窗口的结束位置？

窗口就是 满足其和 ≥ s 的长度最小的 连续 子数组。

窗口的起始位置如何移动：如果当前窗口的值大于s了，窗口就要向前移动了（也就是该缩小了）。

窗口的结束位置如何移动：窗口的结束位置就是遍历数组的指针，也就是for循环里的索引。

其实从中可以发现滑动窗口也可以理解为双指针法的一种！只不过这种解法更像是一个窗口的移动，所以叫做滑动窗口更适合一些。

解题的关键在于窗口的起始位置如何移动，如下图所示：

 

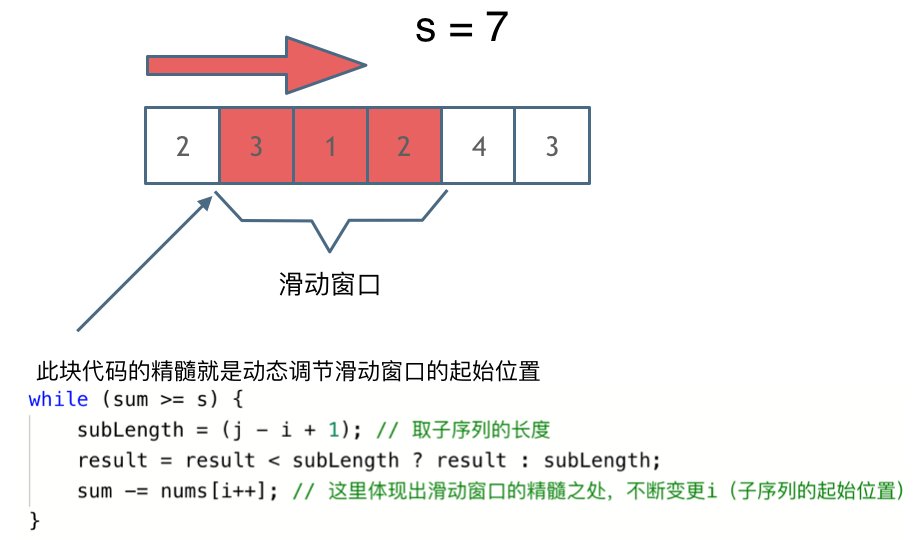
可以发现滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。

因此，可以写出代码：

class Solution {
public:
    int minSubArrayLen(int s, vector<int>& nums) {
        int result = INT32_MAX;
        int sum = 0; // 滑动窗口数值之和
        int i = 0; // 滑动窗口起始位置
        int subLength = 0; // 滑动窗口的长度
        for (int j = 0; j < nums.size(); j++) {
            sum += nums[j];
            // 注意这里使用while，每次更新 i（起始位置），并不断比较子序列是否符合条件
            while (sum >= s) {
                subLength = (j - i + 1); // 取子序列的长度
                result = result < subLength ? result : subLength;
                sum -= nums[i++]; // 这里体现出滑动窗口的精髓之处，不断变更i（子序列的起始位置）
            }
        }
        // 如果result没有被赋值的话，就返回0，说明没有符合条件的子序列
        return result == INT32_MAX ? 0 : result;
    }
};

而这种方法的时间复杂度为：O(n)，空间复杂度为：O(1)。

另外，需要注意的是：不是for里放一个while，其复杂度就是O(n^2)， 时间复杂度主要是看每一个元素被操作的次数，每个元素在滑动窗后进来操作一次，出去操作一次，每个元素都是被操作两次，所以时间复杂度是 2 × n 也就是O(n)。