[LeetCode] 1091. Shortest Path in Binary Matrix

Given an n x n binary matrix grid, return the length of the shortest clear path in the matrix. If there is no clear path, return -1.

A clear path in a binary matrix is a path from the top-left cell (i.e., (0, 0)) to the bottom-right cell (i.e., (n - 1, n - 1)) such that:

  • All the visited cells of the path are 0.
  • All the adjacent cells of the path are 8-directionally connected (i.e., they are different and they share an edge or a corner).

The length of a clear path is the number of visited cells of this path.

Example 1:

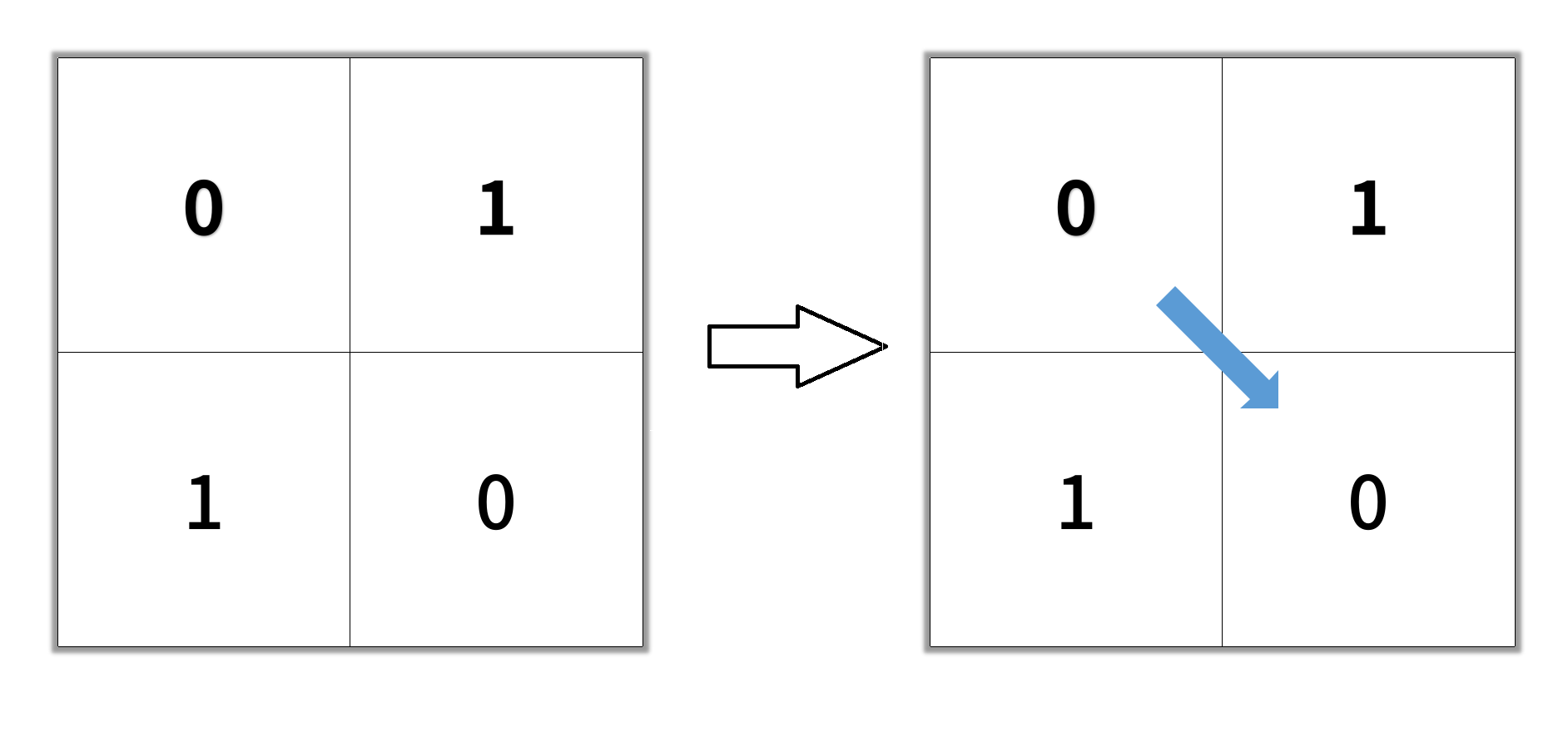
Input: grid = [[0,1],[1,0]]
Output: 2

Example 2:

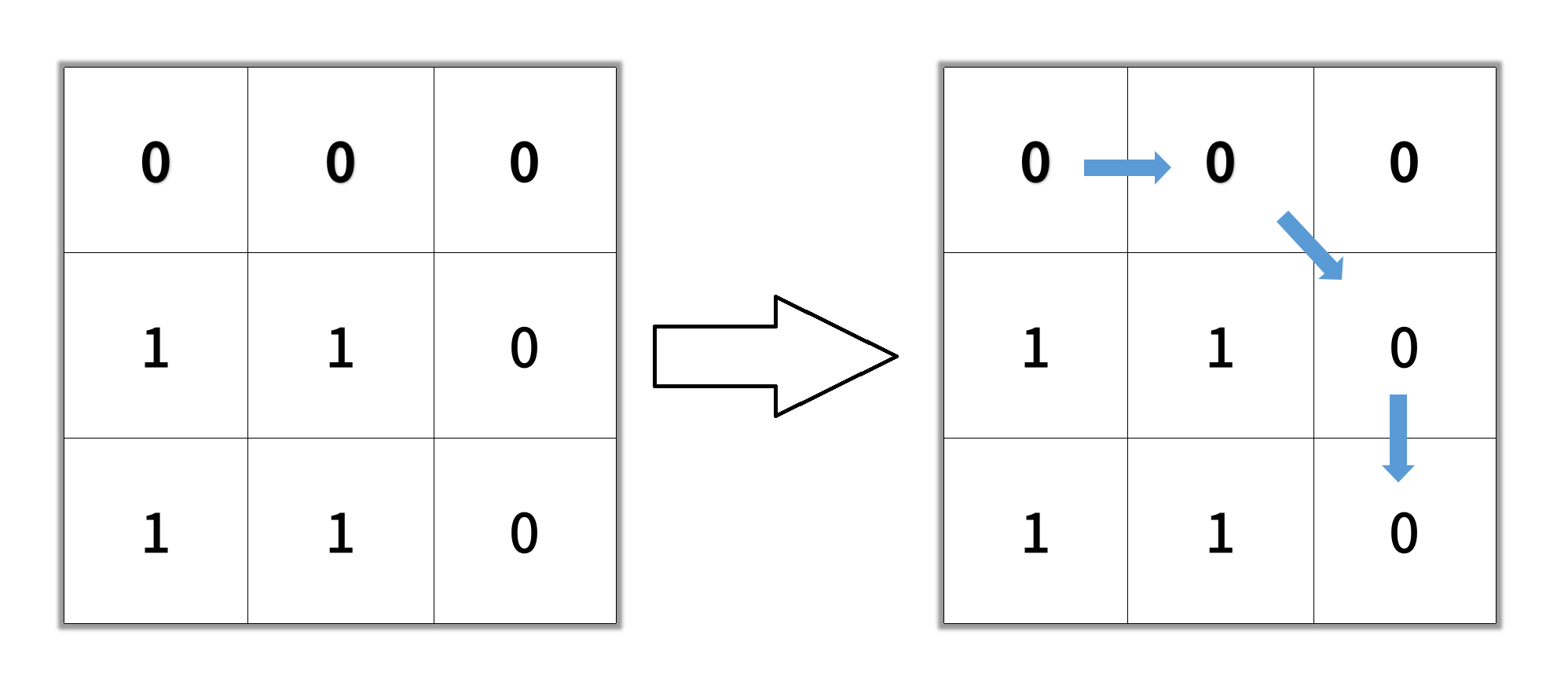
Input: grid = [[0,0,0],[1,1,0],[1,1,0]]
Output: 4

Example 3:

Input: grid = [[1,0,0],[1,1,0],[1,1,0]]
Output: -1

Constraints:

  • n == grid.length
  • n == grid[i].length
  • 1 <= n <= 100
  • grid[i][j] is 0 or 1

二进制矩阵中的最短路径。

给你一个 n x n 的二进制矩阵 grid 中，返回矩阵中最短 畅通路径 的长度。如果不存在这样的路径，返回 -1 。

二进制矩阵中的 畅通路径 是一条从 左上角 单元格（即，(0, 0)）到 右下角 单元格（即，(n - 1, n - 1)）的路径，该路径同时满足下述要求：

路径途经的所有单元格都的值都是 0 。
路径中所有相邻的单元格应当在 8 个方向之一 上连通（即，相邻两单元之间彼此不同且共享一条边或者一个角）。
畅通路径的长度 是该路径途经的单元格总数。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/shortest-path-in-binary-matrix
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

跟大部分的 flood fill 的题型类似，这是一道给一个起点然后问你是否能到达终点的题目。这道题的起点和终点分别是 matrix 的左上角和右下角，无非是这道题的 traverse 的规则是可以往八个方向走，一般的题是只能往四个方向走。同时注意 clear path 的定义是路径上符合题意的单元格（0）的总数，如果你遇到任何坐标值为 1 的点，那就不能走。如果起点或终点的坐标值已经是 1 的话，直接就可以返回了，这是一个 corner case。其他部分就是正常 BFS 题目的翻版，如果不理解可以先做其他 flood fill 的题。

时间O(mn)

空间O(mn) - visited matrix

Java实现

 1 class Solution {
 2     int[][] dirs = new int[][] { { 1, 0 }, { -1, 0 }, { 0, 1 }, { 0, -1 }, { -1, 1 }, { -1, -1 }, { 1, 1 }, { 1, -1 } };
 3 
 4     public int shortestPathBinaryMatrix(int[][] grid) {
 5         int m = grid.length;
 6         int n = grid[0].length;
 7         // corner case
 8         if (grid[0][0] == 1 || grid[m - 1][n - 1] == 1) {
 9             return -1;
10         }
11         // normal case
12         int count = 0;
13         boolean[][] visited = new boolean[m][n];
14         visited[0][0] = true;
15         Queue<int[]> queue = new LinkedList<>();
16         queue.offer(new int[] { 0, 0 });
17         while (!queue.isEmpty()) {
18             int size = queue.size();
19             for (int i = 0; i < size; i++) {
20                 int[] cur = queue.poll();
21                 if (cur[0] == m - 1 && cur[1] == n - 1) {
22                     return count + 1;
23                 }
24                 for (int k = 0; k < 8; k++) {
25                     int nextX = cur[0] + dirs[k][0];
26                     int nextY = cur[1] + dirs[k][1];
27                     if (nextX < 0 || nextX >= m || nextY < 0 || nextY >= n || visited[nextX][nextY] == true
28                             || grid[nextX][nextY] == 1) {
29                         continue;
30                     }
31                     queue.offer(new int[] { nextX, nextY });
32                     visited[nextX][nextY] = true;
33                 }
34             }
35             count++;
36         }
37         return -1;
38     }
39 }

 

二刷再提供一个不需要额外空间的做法。我将已经遍历过的坐标标记成 1，等同于不能走。

时间O(mn)

空间O(1)

Java实现

 1 class Solution {
 2     public int shortestPathBinaryMatrix(int[][] grid) {
 3         int m = grid.length;
 4         int n = grid[0].length;
 5         // corner case
 6         if (grid[0][0] == 1 || grid[m - 1][n - 1] == 1) {
 7             return -1;
 8         }
 9         
10         // normal case
11         int[][] dirs = new int[][] { { 1, 0 }, { -1, 0 }, { 0, 1 }, { 0, -1 }, { -1, 1 }, { -1, -1 }, { 1, 1 }, { 1, -1 } };
12         int step = 0;
13         Queue<int[]> queue = new LinkedList<>();
14         queue.offer(new int[] { 0, 0 });
15         grid[0][0] = 1;
16         while (!queue.isEmpty()) {
17             int size = queue.size();
18             for (int i = 0; i < size; i++) {
19                 int[] cur = queue.poll();
20                 int x = cur[0];
21                 int y = cur[1];
22                 if (x == m - 1 && y == n - 1) {
23                     return step + 1;
24                 }
25                 for (int k = 0; k < 8; k++) {
26                     int newX = x + dirs[k][0];
27                     int newY = y + dirs[k][1];
28                     if (newX >= 0 && newX < m && newY >= 0 && newY < n && grid[newX][newY] == 0) {
29                         grid[newX][newY] = 1;
30                         queue.offer(new int[] { newX, newY });
31                     }
32                 }
33             }
34             step++;
35         }
36         return -1;
37     }
38 }

 

flood fill题型总结

LeetCode 题目总结

posted @ 2021-02-14 08:24  CNoodle  阅读(227)  评论(0)    收藏  举报