[LeetCode] 694. Number of Distinct Islands

You are given an m x n binary matrix grid. An island is a group of 1's (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.

An island is considered to be the same as another if and only if one island can be translated (and not rotated or reflected) to equal the other.

Return the number of distinct islands.

Example 1:

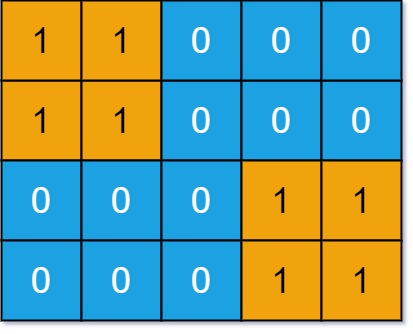
Input: grid = [[1,1,0,0,0],[1,1,0,0,0],[0,0,0,1,1],[0,0,0,1,1]]
Output: 1

Example 2:

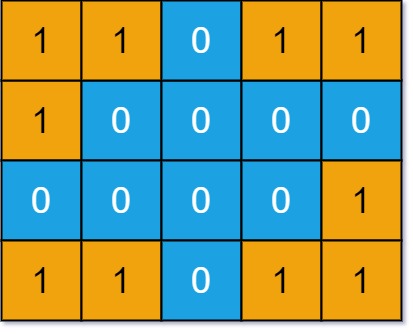
Input: grid = [[1,1,0,1,1],[1,0,0,0,0],[0,0,0,0,1],[1,1,0,1,1]]
Output: 3

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 50
• grid[i][j] is either 0 or 1.

不同岛屿的数量。

给定一个非空 01 二维数组表示的网格，一个岛屿由四连通（上、下、左、右四个方向）的 1 组成，你可以认为网格的四周被海水包围。

请你计算这个网格中共有多少个形状不同的岛屿。两个岛屿被认为是相同的，当且仅当一个岛屿可以通过平移变换（不可以旋转、翻转）和另一个岛屿重合。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/number-of-distinct-islands
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路还是跟200题差不多，也是dfs做，但是这里需要注意的是如何判断岛屿是不是重复的。我这里给出discussion最高票答案的思路。这其实是一个把信息序列化的思路，序列化的思想类似297题。既然是判断是否有重复的路径，那么应该是会利用到哈希来判断是否重复。但是如何将路径放入哈希呢，只能是序列化。这里hashset存的是一个岛屿被DFS过的路径。举个例子，当一开始在矩阵里面扫描的时候，遇到一个1，就开始做DFS递归遍历去他的四个方向再找1。此时可以将一开始找到的1 append到一个StringBuilder里面并且用“o”标记它为（目前这个岛的）原点original。DFS往四个方向遍历的时候，同时也往StringBuilder里面标记各自的方向。在不考虑翻转和旋转的情况下，可以有效查找出不同的岛屿。回溯的时候记得多加一个字母表示回溯，否则类似这样的case是判断不出来的。

/** WARNING: DO NOT FORGET to add path for backtracking, otherwise, we may have same result when we count two 
     * distinct islands in some cases
     * 
     * eg:              1 1 1   and    1 1 0
     *                  0 1 0          0 1 1
     * with b:          rdbr           rdr
     * without b:       rdr            rdr
     * */

时间O(mn)

空间O(n)

Java实现

class Solution {
    public int numDistinctIslands(int[][] grid) {
        Set<String> set = new HashSet<>();
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                if (grid[i][j] != 0) {
                    StringBuilder sb = new StringBuilder();
                    dfs(grid, i, j, sb, "o");
                    grid[i][j] = 0;
                    set.add(sb.toString());
                }
            }
        }
        return set.size();
    }

    private void dfs(int[][] grid, int i, int j, StringBuilder sb, String dir) {
        if (i < 0 || i == grid.length || j < 0 || j == grid[0].length || grid[i][j] == 0) {
            return;
        }
        sb.append(dir);
        grid[i][j] = 0;
        dfs(grid, i - 1, j, sb, "u");
        dfs(grid, i + 1, j, sb, "d");
        dfs(grid, i, j - 1, sb, "l");
        dfs(grid, i, j + 1, sb, "r");
        // backtracking
        sb.append("b");
    }
}

 

flood fill题型总结

LeetCode 题目总结