1.
package com.itheima.Main;
import java.util.ArrayList;
import java.util.List;
/**
* 小蓝有一个超大的仓库,可以摆放很多货物。
* 现在,小蓝有 n 箱货物要摆放在仓库,每箱货物都是规则的正方体。小蓝
* 规定了长、宽、高三个互相垂直的方向,每箱货物的边都必须严格平行于长、
* 宽、高。
* 小蓝希望所有的货物最终摆成一个大的立方体。即在长、宽、高的方向上
* 分别堆 L、W、H 的货物,满足 n = L × W × H。
* 给定 n,请问有多少种堆放货物的方案满足要求。
* 例如,当 n = 4 时,有以下 6 种方案:1×1×4、1×2×2、1×4×1、2×1×2、2 × 2 × 1、4 × 1 × 1。
* 请问,当 n = 2021041820210418 (注意有 16 位数字)时,总共有多少种方案?
*
*/
public class Test {
public static void main(String[] args) {
/**
* 根据题目要求,L与W以及H相乘必须等于n。可以发现,如果一个数可以由三个数相乘得到,
* 那么这三个数一定都是这个数的因数。举个例子:24,1* 2*12= 24,2*2* 6 = 24等等。
* 考虑到这里,解法就呼之欲出了,填空题可以直接暴力。先求出 n的所有因数,这里注意必须是所有的因数,
* 包括n本身,然后三层循环遍历搜索即可。
*/
List<Long> yz=new ArrayList<>();//存放因子的集合
long n =2021041820210418L;
for(long i=1;i<Math.sqrt(n);i++){
if(n%i==0){//每次将它的因子加进去
yz.add(i);
yz.add(n/i);
}
}
System.out.println(yz);
int count=0;
for(int i=0;i<yz.size();i++){
for (int j = 0; j <yz.size() ; j++) {
for (int k = 0; k < yz.size(); k++) {
if(yz.get(i)*yz.get(j)*yz.get(k)==n){
count++;
}
}
}
}
System.out.println(count);
}
}
2.
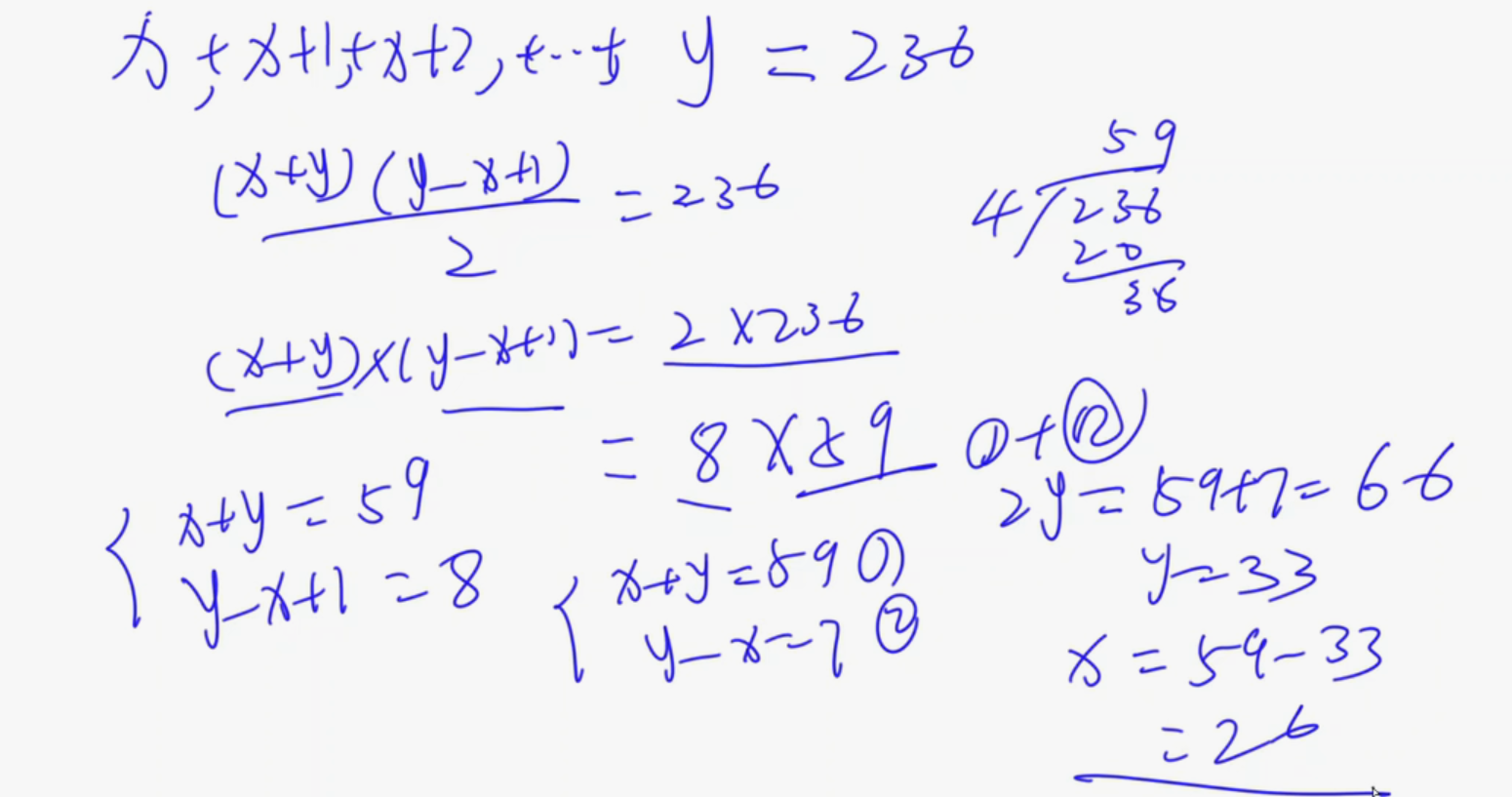
package com.itheima.Main;
/**
* 某君从某年开始每年都举办一次生日party,并且每次都要吹熄与年龄相同根数的蜡烛。现在算起来,他一共吹熄了236根蜡烛。
请问,他从多少岁开始过生日party的?
用枚举逐个遍历所有的年龄,再累加到sum上,在每次循环过后进行判断即可。
*/
public class Main2 {
public static void main(String[] args) {
int sum=0;
for(int i=1;i<100;i++){
sum=0;
for(int j=i;j<100;j++){
sum+=j;
if(sum>236) break;
if(sum==236){
System.out.println(i);
}
}
}
}
}
3.
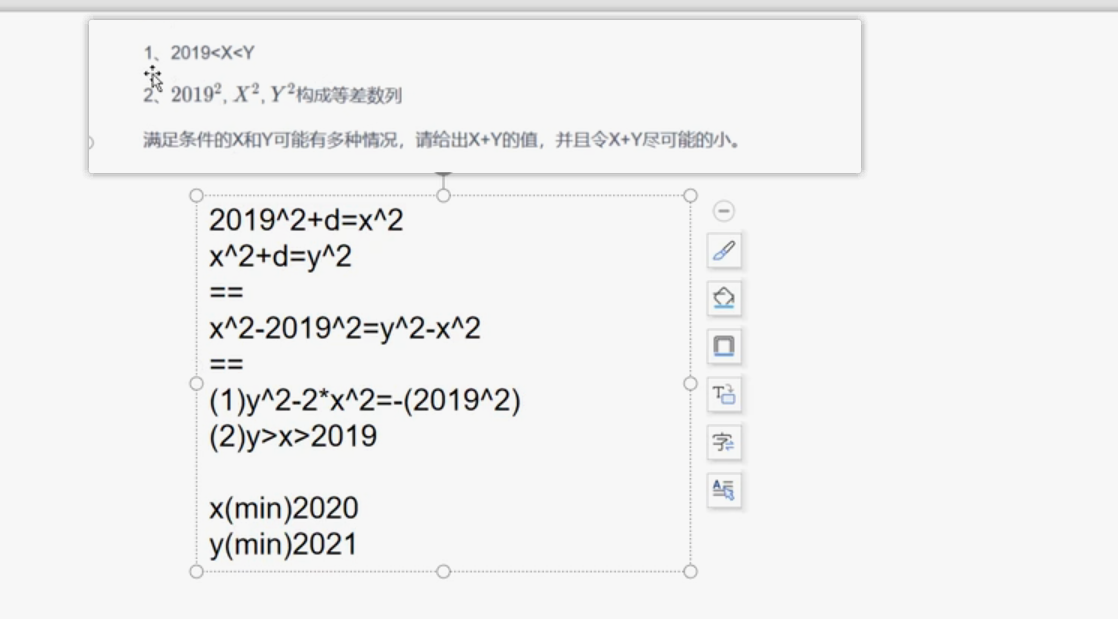
直接暴力枚举
package com.itheima.Main;
public class Main3 {
public static void main(String[] args) {
int temp=-1*2019*2019;
for (int i = 2020; i < 9000; i++) {
for (int j = i+1; j <9000 ; j++) {
int y2=j*j;
int x2=i*i;
if(y2-2*x2==temp){
System.out.println(i+j);
}
}
}
}
}
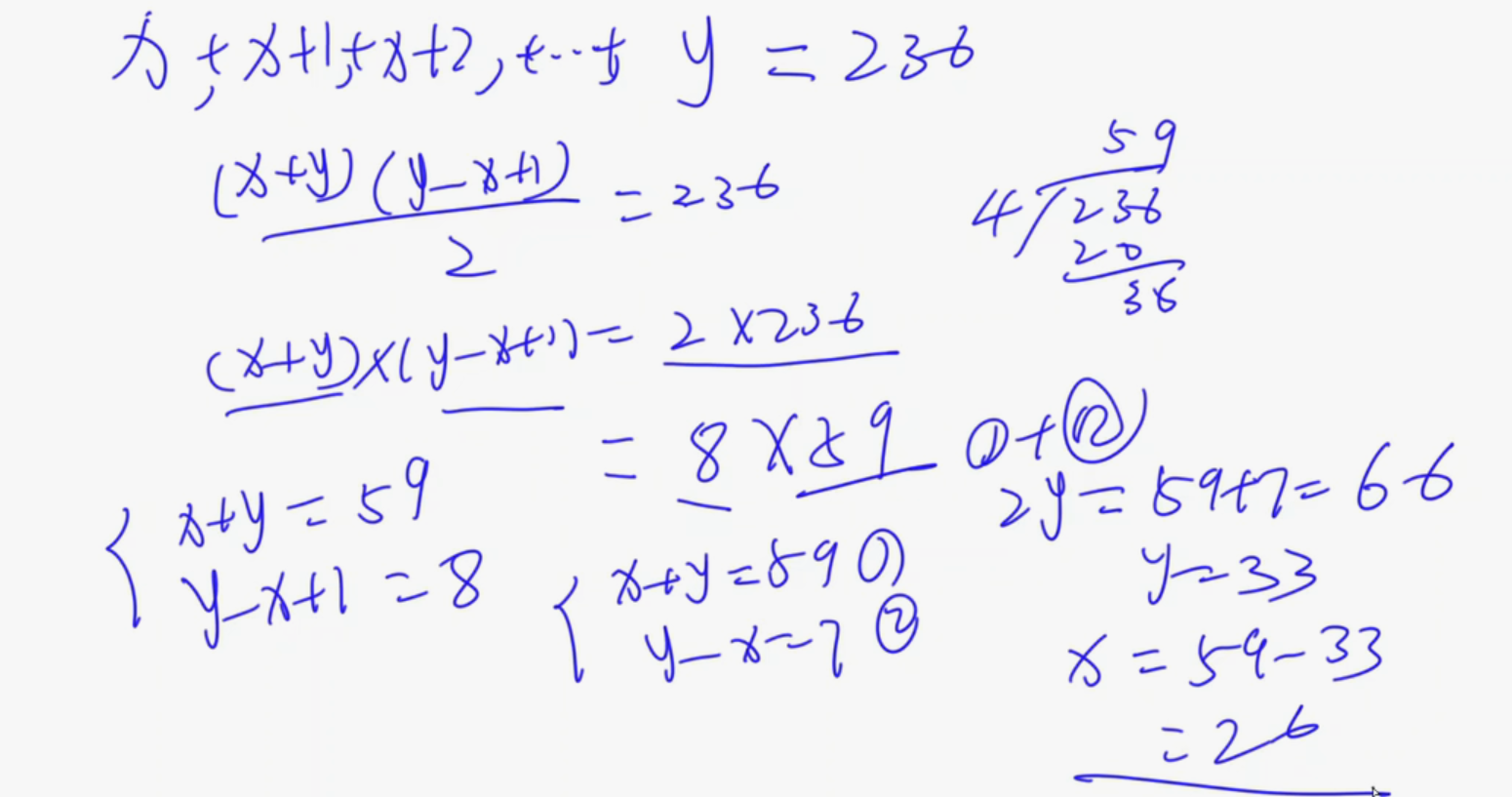



 浙公网安备 33010602011771号
浙公网安备 33010602011771号