动态规划

动态规划的思想是将一个问题分解为若干个子问题，对每个子问题求最优解，前一个子问题的最优解，为下面的子问题提供了有效信息，依次解决子问题，最后一个子问题就是初始问题的最优解。动态规划应用于子问题重叠的情况，子问题的划分是通过递归实现。为了避免子问题的重复计算，保证每个子问题只求解一次，会将解保存在数组中。

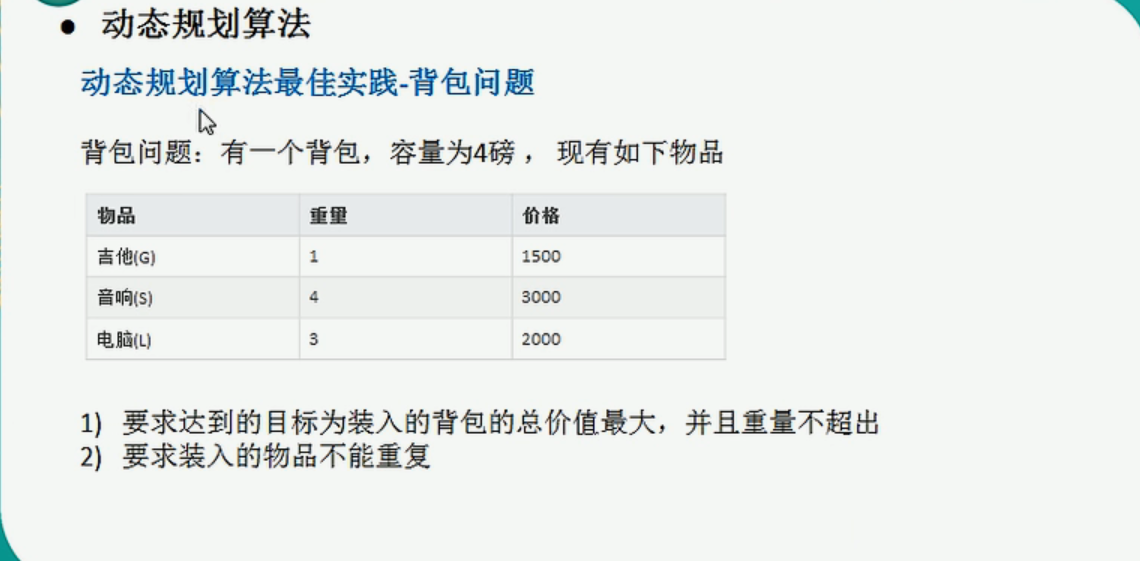
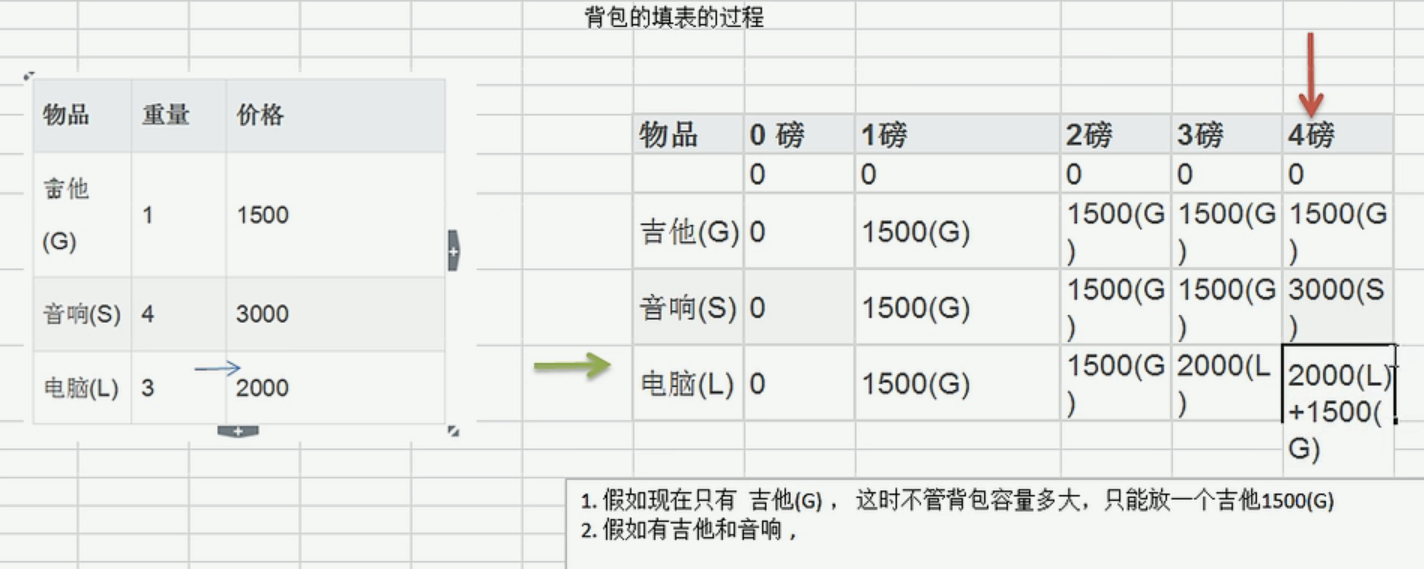
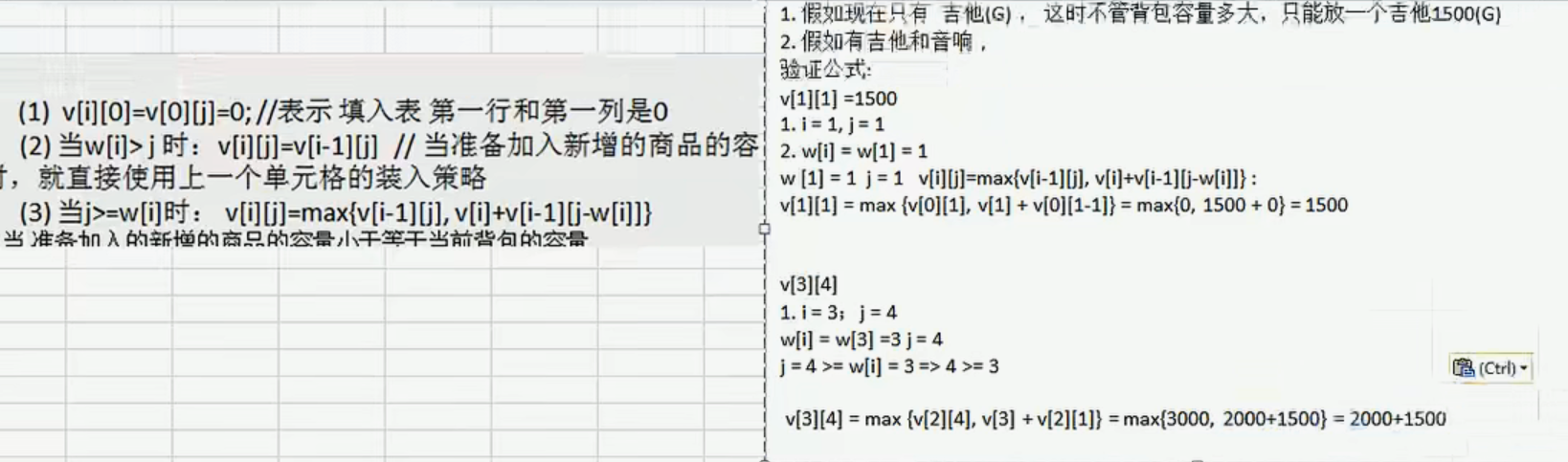
第(3)有两种情况，一种是使用上一个装入的最大值v[i-1][j]，另一种是当前商品的价值+装入i-1商品到剩余空间的最大值对比上面的表格看。
也就是如果能装进背包，是看原来策略的价值更大，还是新装入商品的价值加上剩余空间的最大值

package com.itheima.Main;

public class KnapsackProblem {
    public static void main(String[] args) {
        int[] w={1,4,3};//物品的重量
        int[] val={1500,3000,2000};//物品的价值,这里的val[i]就是前面讲的v[i]
        int m=4;//背包的容量
        int n=val.length;//物品的个数

        //创建二维数组
        //v[i][j]表示前i个物品能够装入容量为j的背包中的最大价值
        int[][] v=new int[n+1][m+1];//因为表格的前面新加了一行和一列

        //初始化第一行和第一列，这里本程序中，可以不去处理，因为默认是0
        for (int i = 0; i < v.length; i++) {
            v[i][0]=0;//将第一列设置为0
        }
        for (int i = 0; i < v[0].length; i++) {
            v[0][i]=0;
        }

        //根据前面得到公式来动态规划处理
        for (int i = 1; i <v.length ; i++) {//i是1开始的 不处理第一行
            for (int j = 1; j < v[0].length; j++) {//j是从1开始的 不处理第一列
                //公式
                if(w[i-1]>j){//因为i是从1开始的，所以公式中的w[i]修改成w[i-1]
                    v[i][j]=v[i-1][j];
                }else{
                    //说明 原公式： v[i][j]=Math.max(v[i-1][j],v[i-1]+v[i][j-w[i]]);
                    //因为我们的i是从1开始的，因此公式需要调整为
                    v[i][j]=Math.max(v[i-1][j],val[i-1]+v[i-1][j-w[i-1]]);
                }
            }
        }


        //输出v，看看当前情况
        for(int i =0;i<v.length;i++){
            for(int j=0;j<v[i].length;j++){
                System.out.print(v[i][j]+" ");
            }
            System.out.println();
        }
    }
}