IEEE浮点数表示

浮点数表示

IEEE浮点标准用\(V = (-1)^s * M * 2^E 的形式来表达一个数\)：

• 符号（sign） s决定这个数是负数（s=1)还是正数（s=0),而对于数值0的符号解释作为特殊情况处理。
• 尾数（significand）M是一个二进制小数，它的范围是1_{2-ω，或者是0}1-ω。
• 价码（exponent) E的作用是对浮点数加权，这个权重是2的E次幂（可能是负数）。

将浮点数的位表示划分为三个字段，分别对这些值进行编码：

1. 单独一个的符号位s直接龚方雄符号s.
2. k位的阶码字段\(exp=e_{k-1}...e_1e_0编码阶码E。\)
3. n位小数字段\(frac =f_{n-1}...f_1f_0\)编码尾数M，但是编码出来的值也依赖于阶码字段的值是否等于0。

对单精度float类型32位长度，s=1 ,k=8,n=25.规定了位表示后，根据k值分为三种情况:

情况1：规格化的值
这是最普遍的情况。当exp阶码字段的位模既不全为0（数值为0），也不全为1（单精度数为\(2^8-1=255，双精度数2^{11}-1=2047\))时，都属于这类情况。
阶码被 解释为以偏置（bisaed)形式表示的有符号整数。即E=e-bisa,其中e是无符号数，其位表达为\(e_{k-1}...e_1e_0\),而bias是一个等于\(2^{k-1}-1的偏置值（单精度为127，双精度为1023）\)。由此产生的指数的取值范围，对于单精度是-126_{127，双精度是-1022}1023。

对于小数字段frac的解释为描述小数值f,其中 0 ≥ f＜1，其二进制表示为\(0.f_{n-1}...f_1f_0\),尾数定义为M =1+f.这种方式也叫隐含的以1开头的表示，因为我们可以把M看成一个二进制表达式为\(1.f_{n-1}...f_1f_0\)的数字。既然我们总是能够调整阶码E，使得尾数M在范围1 ≤ M＜2之中，那么这种表示是一种轻松获得一个额外精度位的技巧。

情况2：非规格化的值
当阶码域为全0时， 所表示的数是非规格化形式。在这种情况下E =1-Bias,而尾数M= f,也就是不含隐含的开头1.

对于非规格化的值为什么这样设置偏置值？
使阶码值为1 - Bias而不是简单地用0-Bias，似乎是违反直觉的，我们将很快看到，这种方式提供了一种从非规格化值平滑转换到规格化值的方法。

• 非规格化数有两个用途：

1. 一种表示数值0的方法。因规格化数，我们必须使M ≥ 1，这样就不能表示0了。实际上，+0.0的浮点表示位模式为全0.
2. 非规格化数的别外一个功能是表示那些非常接近0.0的数。

情况3：特殊值
最后一类数值是指当阶码全为1的时候出现的。

• 当小数域中全为0时，得到的值表示无穷，
  s =1时，为正无穷，s =0时，为负无穷。-----当我们返回两个非常大或小的值相乘可以表示溢出的结果.
• 当小数域为非零时，结果值被称为“NaN”,即返回这样的NaN值。

重要和单精度和双精度浮点数的表示和数字值

描述	exp	frac	单精度值	十进制	双精度值	双精度十进制
0	00...00	0...00	0	0.0	0	0.0
最小非规格化数	00...00	0...01	\(2^{-23}*2^{-126}\)	\(1.4*10^{-45}\)	\(2^{-52}*2^{-1022}\)	\(4.9*10^{-324}\)
最大非规格化数	00...00	1...11	\((1-2^{-23})-2^{-126}\)	\(1.2*10^{-38}\)	\((1-2^{-52})-2^{-1022}\)	\(2.2*10^{-308}\)
最小规格化数	00...01	0...00	\(1*2^{-126}\)	\(1.2*10^{-38}\)	\(1*2^{-1022}\)	\(2.2*10^{-308}\)
1	01...11	0...00	\(1*2^0\)	1.0	\(1*2^0\)	1.0
最大规格化数	00...10	1...11	\((2-2^{-23}）*2^{127}\)	\(3.4*10^{38}\)	\((2-2^{52})*2^{1023}\)	\(1.8*10^{308}\)

上表为非负浮点数示例。

定点、浮点表示的区别（字长相同）

1.数值的表示范围：浮点数远超定点数。
2.精度：浮点数精度降低了。
3.数的运算：浮点数运算更加复杂。
4.溢出问题：运算结果超过尾数范围却不一定溢出，只有规格化后阶码超过所能表示范围时才发生溢出。

浮点数的加减运算

对阶:

 使两个操作数的小数点对其，小阶向大阶靠齐。（右移）  

尾数求和

将对阶后的尾数按定点数加减运算规则运算。  运算结果不一定是规格化的，需要进一步进行规格化处理。  

规格化

同之前说明的一样。  

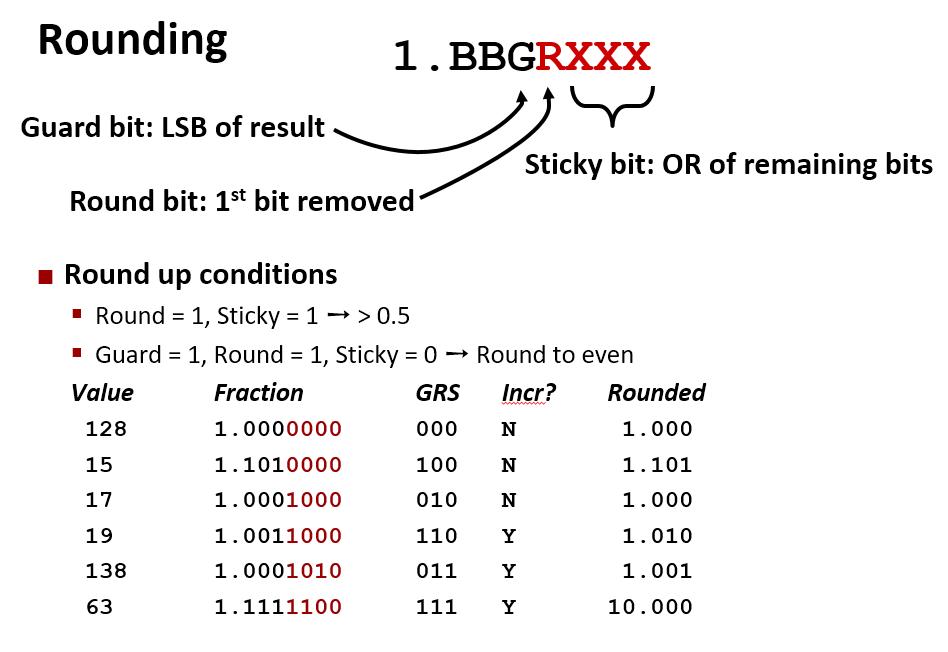
舍入Rounding

• 因为表示方法限制了浮点数的范围和精度，所以浮点运算只能近似表示实数运算！！
• 关键问题是向上、向下如何确定舍入的方向？
• IEEE浮点格式定义了四种不同的舍入方式。

1. 向偶数舍入(round-to-even),也称为最接近的值舍入(round-to-nearest),是默认的方式。

口诀： 四舍六入五成双，或者四舍六入五凑偶。当然这句通俗的口诀是针对十进制来说的。
向偶数舍入只有两条规则:
 a. 如果最接近的值唯一，则直接向最接近的值舍入（对应口诀中的“四舍六进”）；
 b. 如果是处在“中间值”，那么要看保留位(Guard bit)是否是偶数，如果是偶数则直接舍去后面的数不进位，如果是奇数则进位后再舍去后面的数。
 只要理解了上面两条规则，那么就完全掌握了向偶数舍入。（对应口诀中的“五成双”）
几个概念：

1. 保留位(Guard bit)、近似位(Round bit)和粘滞位(Sticky bit)

• 对于十进制数来讲：
    如果我们想保留两位小数，即留下十分位和百分位上的数。那么保留位(Guard bit)就是结果的最低位，即百分位；近似位(Round bit)就是第一个被舍掉的位，即千分位；而千分位之后的所有位（包括万分位、十万分位等等）合起来构成粘滞位(Sticky bit)。
• 对于二进制数：
    如果我们想要保留两位小数，那么小数点右边第二位就是保留位(Guard bit)，小数点右边第三位就是近似位(Round bit)，小数点右边第四位开始一直向右的所有小数位或起来构成粘滞位(Sticky bit)。用CMU的课件也许更容易理解一点。
  

2.中间值 :引入一个中间值的概念,这对于理解 “向偶数舍入” 至关重要。
  对于十进制来说，如果要保留一位小数，即百分位和百分位之后的小数都会被近似掉，那么此时中间值就是xxx.x5000…（5之后全零）。
也就是说，求中间值的方法如下：

1). 保留位(Guard bit)和左边的数字保持不变；
2). 近似位(Round bit)改写为N/2（N为进制数，十进制就是10，二进制就是2）
3). 粘滞位(Sticky bit)全部写零

原始值(十进制)	中间值(保留1位小数)	中间值(保留2位小数)
1.334	1.350	1.335
1.622	1.650	1.625
1.744	1.750	1.745
1.488	1.450	1.485

原始值(二进制)	中间值(保留1位小数)	中间值(保留2位小数)
1.101	1.110	1.101
101.111	101.110	101.111
11.001	11.010	11.001
1.010	1.010	1.011
1.100	1.110	1.101

举例说明向偶数舍入：

原始值(十进制)	中间值	近似值(向偶数舍入)	说明（对于以下的例子中，我们采用向偶数舍入，保留精确度十分位，即保留1位小数）
1.36	1.35	1.4	原始值都比中间值要大，也就是“四舍六入五成双”中的“六入”。所以都向十分位进一，从而使得损失的精度最小。
1.751	1.75	1.8	同上
1.45001	1.45	1.5	同上
1.33	1.35	1.3	原始值都比中间值要小，也就是“四舍六入五成双”中的“四舍”。所以直接舍弃，不进位，从而使得损失的精度最小。
1.82	1.85	1.8	同上
1.71	1.75	1.7	同上
1.35	1.35	1.4	原始值和中间值相等，也就是“四舍六入五成双”中的“五成双”。
1.25	1.25	1.2	对于这些和中间值完全相等的原始值，我们考察保留位(Guard bit)，如果保留位是偶数，则直接舍弃近似位(Round bit)和粘滞位(Sticky bit)；如果保留位是奇数，则先向保留位进一，之后舍弃近似位(Round bit)和粘滞位(Sticky bit)。这样，结果中的保留位就是偶数了。这就是向偶数舍入 名字的由来

原始值(二进制)	中间值	近似值(向偶数舍入)	说明（对于以下二进制的数值，我们采用向偶数舍入的方式，保留一位小数）
1.111	1.11	10.0	原始值都比中间值要大，也就是“四舍六入五成双”中的“六入”。所以向小数点右边第1位进一，从而使得损失的精度最小。
1.0101	1.01	1.1	同上
1.0111	1.01	1.1	同上
1.001	1.01	1.0	原始值都比中间值要小，也就是“四舍六入五成双”中的“四舍”。所以直接舍弃，不进位，从而使得损失的精度最小。
1.10	1.11	1.1	同上
1.110	1.11	10.0	原始值和中间值相等，也就是“四舍六入五成双”中的“五成双”。对二进制0为偶数，1为奇数。
1.010	1.01	1.0	对于这些和中间值完全相等的原始值，我们考察保留位(Guard bit)，如果保留位是偶数，则直接舍弃近似位(Round bit)和粘滞位(Sticky bit)；如果保留位是奇数，则先向保留位进一，之后舍弃近似位(Round bit)和粘滞位(Sticky bit)。这样，结果中的保留位就是偶数了。这就是向偶数舍入 名字的由来

2. 向零舍入

向零舍入是把正数向“下”舍入，把负数“上”舍入。（向“零”的方向）

3. 向上舍入 （朝正无穷舍入）

对正数而言，只要多余位不全为0则向最低有效位进1；负数则直接截尾。

4.向下舍入（朝负无穷舍入）

对负数而言，向最低有效位进1；正数若多余位不全部为0则简单截尾。

四种舍入示例：（十进制，保留整数位）

方式	1.40	1.60	1.50	2.50	-1.50
向偶数舍入	1	2	2	2	-2
向零舍入	1	1	1	2	-1
向上舍入	2	2	2	3	-1
向下舍入	1	1	1	2	-2

溢出判断

看阶码是否溢出，阶码的值过大，指数上溢；过小，指数下溢。   
并不是看尾数是否溢出，尾数溢出可以通过右移得到纠正。

C语言中的浮点数类型

1. int--->float，不会发生溢出，但会影响精度。
2. int/float--->double，double的有效位数更多，因此能够保留精度。
3. double---->float，可能会发生溢出，发生舍入。
4. float/double--->int，向0方向截断，发生舍入，可能会溢出。