整除分块（数论分块）详解
整除分块（数论分块）
介绍
在求解问题
时，若 \(n\) 的范围很大那么 \(\Theta(n)\) 求解将会超时，我们需要一种更高效的方法来计算，整除分块就是这样一种方法
不难发现，在 \(i\) 取某些值的时候 \(\lfloor\frac ni\rfloor\) 的值都是相同的，考虑将 \(\lfloor\frac ni\rfloor\) 的值相同的 \(i\) 一起计算，减少计算次数
那么此时我们需要计算多少次呢？
当 \(i\le\sqrt n\) 时显然 \(\lfloor\frac ni\rfloor\) 的取值只有 \(\sqrt n\) 种可能，而当 \(i>\sqrt n\) 时有 \(\frac ni<\sqrt n\) ，所以 \(\lfloor\frac ni\rfloor\) 的取值同样只有 \(\sqrt n\) 种可能，也就是说 \(\lfloor\frac ni\rfloor\) 的取值只有 \(2\sqrt n\) 种可能，对于同样的取值只用计算一次，总的时间复杂度也就是 \(\Theta(\sqrt n)\)
下面来说具体怎么做
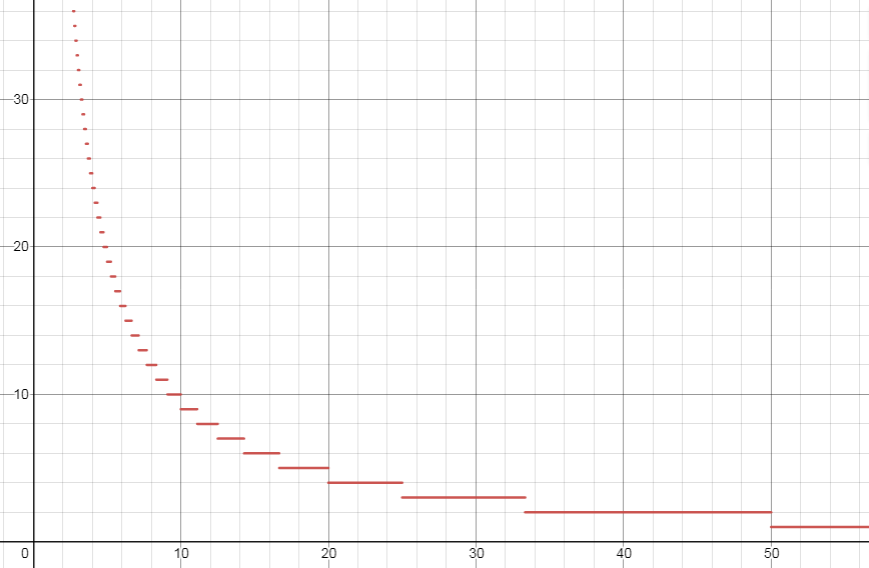
画出 \(\lfloor\frac ni\rfloor\) 的图像不难发现，所有取值相同的 \(i\) 都是连续的整块的，这也是这个算法叫做整除分块的原因，对于每一块我们想要通过给出这一块的左端点，\(\Theta(1)\) 计算出这一块的右端点，这样才能保证复杂度
假设现在我们的左端点是 \(l\)，那么设 \(\lfloor\frac nl\rfloor=k\)，我们要求右端点也就是最大的 \(r=l+d\) 使得 \(\lfloor\frac n{l+d}\rfloor=\lfloor\frac nl\rfloor=k\)
把 \(\lfloor\frac nl\rfloor\) 和 \(\lfloor\frac n{l+d}\rfloor\) 展开得 \(n=kl+p\) 和 \(n=k(l+d)+p'\)，其中 \(1\le p<l\)
那么 \(kl+p=k(l+d)+p'\) 所以 \(p'=p-kd\)，因为 \(p'\ge0\)，所以 \(kd\le p\)，所以 \(d\le\frac pk\)，又因为 \(d\) 为整数，所以 \(d\) 最大能取 \(\lfloor\frac pk\rfloor\)，其中 \(p=n\bmod l=n-l\lfloor\frac nl\rfloor\)，\(k=\lfloor\frac nl\rfloor\)
所以我们有
也就是说，对于每一个左端点为 \(l\) 的块，它的右端点为 \(\lfloor\frac n{\lfloor\frac nl\rfloor}\rfloor\)
求 \(\sum\limits_{i=1}^n\lfloor\frac ni\rfloor\) 我们从左端点 \(l\) 为 \(1\) 开始枚举，每次右端点 \(r\) 取 \(\min(n,\lfloor\frac n{\lfloor\frac nl\rfloor}\rfloor)\)，将答案累加上 \((r-l+1)\lfloor\frac nl\rfloor\)，然后令 \(l=r+1\) 不断循环，当右端点等于 \(n\) 时停止循环
练习
练习一
题目大意
给定 \(n\) 求 \(\sum\limits_{i=1}^nd(i)\)，其中 \(d(i)\) 表示 \(i\) 的约数个数
题解
\(1\) 到 \(n\) 的约数显然只能也在 \(1\) 到 \(n\) 内，那么考虑换一种方式表达 \(\sum\limits_{i=1}^nd(i)\)，枚举 \(1\) 到 \(n\) 的所有数，看枚举的数属于多少个数的约数，假设当前枚举到数字 \(k\) 那么在 \(1\) 到 \(n\) 内 \(k\) 属于多少个数的约数，那么也就是在问在 \(1\) 到 \(n\) 内 \(k\) 的倍数有多少个，显然有 \(\lfloor\frac nk\rfloor\) 个，题目也就转换为了求解 \(\sum\limits_{i=1}^n\lfloor\frac ni\rfloor\)，整除分块即可
练习二
题目大意
给定 \(n,k\)，求 \(\sum\limits_{i=1}^nk\bmod i\)
题解
\(k\bmod i\) 可以写作 \(k-i\lfloor\frac ki\rfloor\)，原式即变为 \(\sum\limits_{i=1}^nk-i\lfloor\frac ki\rfloor=kn-\sum\limits_{i=1}^ni\lfloor\frac ki\rfloor\)，考虑对于 \(\sum\limits_{i=1}^ni\lfloor\frac ki\rfloor\) 使用整除分块，对于值相同的 \(\lfloor\frac ki\rfloor\)，利用等差数列求和公式算出 \(i\) 的区间和，再乘以 \(\lfloor\frac ki\rfloor\) 就可以 \(\Theta(1)\) 累加进答案
再看整除分块时 \(n,k\) 的上界问题，当 \(n\ge k\) 时 \(i>k\) 的部分贡献均为 \(0\)，所以我们忽略 \(n\) 比 \(k\) 大的部分，直接以 \(k\) 为上界计算 \(\sum\limits_{i=1}^k\lfloor\frac ki\rfloor\) 即可；当 \(n<k\) 时每次右端点变为 \(\min(n,\lfloor\frac k{\lfloor\frac kl\rfloor}\rfloor)\)，右端点到 \(n\) 时停止
该文为本人原创，转载请注明出处
