题解 CF960E Alternating Tree

0.前言

如果NOIP上先做那道树形DP，情况又会如何呢

1.正文

手推一下就知道，一条经过点数为偶数个的路径对答案没有任何贡献。因此直接统计经过奇数个点的路径

长度：路径上节点的个数
设\(f[i][0/1]\)：以\(i\)为根的子树中起点为i，长度为偶数/奇数的有向路径的价值和
\(size[i][0/1]\)：以\(i\)为根的子树中长度为偶数/奇数的有向路径数
\(ans\)：最终答案

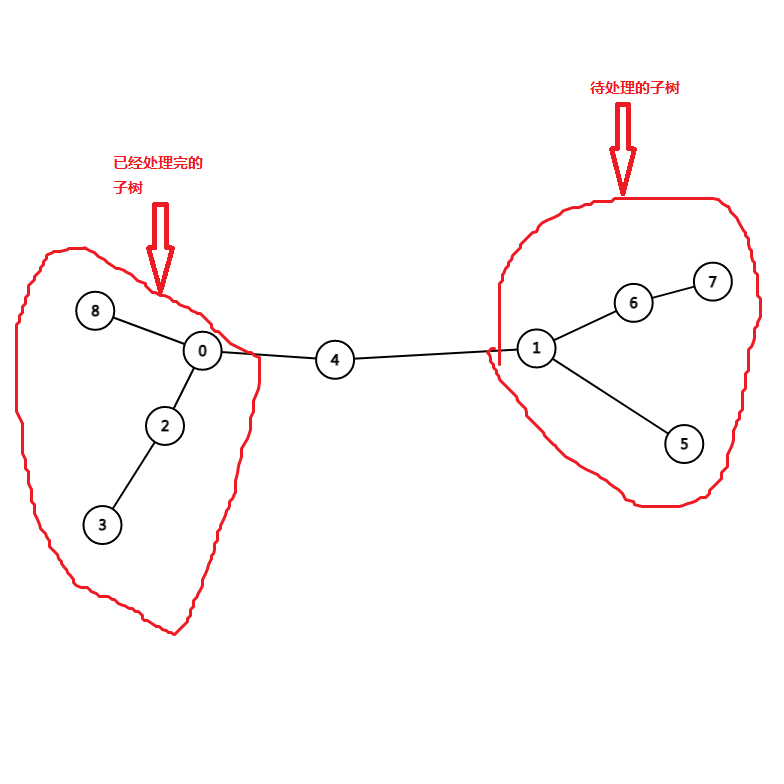
通过上面的图可以很显然地看出
对于一个待处理的子树，它对答案的贡献是这样的

1. 子树奇+父亲偶
   类似于配对，注意正负变化
   \(gongxian+=size[son(i)][1]*(-f[i][0])\)
   \(gongxian+=size[i][0]*f[son(i)][1]\)
2. 子树偶+父亲奇
   注意这个要求子树本身有偶数路径
   \(gongxian+=size[son(i)][0]*f[i][1]\)
   \(gongxian+=size[i][0]*(-f[son(i)][1])\)

然后对贡献乘2加入到答案中就好了

注意同时更新\(f[i][0]\)和\(f[i][1]\)

code

// Problem: Alternating Tree
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/CF960E
// Memory Limit: 250 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long 
using namespace std;
const ll INF=1e18+7,mod=1e9+7;
const int MAXN=2e5+3;
ll n,val[MAXN];
ll ans,f[MAXN][2],size[MAXN][2];
vector<int> tree[MAXN];
void dfs(int num,int fa){
	ll k=-1,gongxian=0;
	f[num][1]=val[num];
	size[num][1]=1;
	ans=(ans+f[num][1])%mod;
	for(auto i:tree[num]){
		if(i==fa) continue;
		dfs(i,num);
		gongxian=0;
		gongxian=(gongxian+((k*f[num][0]%mod+mod)%mod)*(size[i][1]%mod))%mod;
		gongxian=(gongxian+(f[i][1]%mod)*(size[num][0]%mod))%mod;
		gongxian=gongxian*2LL%mod;
		ans=(ans+gongxian)%mod;
		if(size[i][0]){
			gongxian=0;
			gongxian=(gongxian+(f[num][1]%mod)*(size[i][0]%mod))%mod;
			gongxian=(gongxian+((k*f[i][0]%mod+mod)%mod)*(size[num][1]%mod))%mod;
			gongxian=gongxian*2LL%mod;
			ans=(ans+gongxian)%mod;
		}			
		size[num][0]+=size[i][1];
		f[num][0]+=k*f[i][1]+val[num]*size[i][1];
		if(size[i][0]){
			size[num][1]+=size[i][0];
			f[num][1]+=k*f[i][0]+val[num]*size[i][0];
		}
	}
}
int main(){
    ios::sync_with_stdio(false);
    cin>>n;
    for(int i=1;i<=n;i++){	
    	cin>>val[i];
    }
    for(int j=1;j<n;j++){
    	int x,y;
    	cin>>x>>y;
    	tree[x].push_back(y);
    	tree[y].push_back(x);
    }
    dfs(1,0);
    // for(int i=1;i<=n;i++){
    	// cerr<<"A:"<<f[i][0]<<" "<<f[i][1]<<endl;
    // }
    while(ans<0) ans+=mod;
    cout<<ans<<endl;
    return 0;
}