【小白学算法】叉积 ——>"×"乘

作用：用于判断两个向量的位置关系

如点\(A(a.x,a.y),B(b.x,b.y),C(c.x,c.y)\)

A，B为已存在集合里的点，现在要新加入点C，需判断是否需要删除B点

则需判断向量AB与向量AC的位置关系，

其中×乘的定义为\(a×b＝x1*y2-x2*y1＝t\)

• t=0，ab共线（同向或反向）

• t>0，a在b的顺时针方向

• t<0，a在b的逆时针方向

所以\(AB×AC=(b.x-a.x)*(c.y-a.y)-(b.y-a.y)*(c.x-a.x)=t\)

可根据凸包的类型判断是否需要删除

eg.上凸包

t>0时，AB在AC的顺即新加的点C在AB的逆方向，此时上凸包会把B点包裹在内，因此B点可以删除。

t<0时，AB在AC的逆即新加的点C在AB的顺方向，此时B不会被包裹，在当前凸包中以顶点出现，因此无需删除。

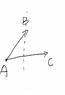
t=0，由于我们在遍历点时会按照一定的顺序，如从最左或最右开始，因此只要我们在遍历过程中出现t=0即共线这种情况，就一定是同向共线，那么即可判断B点在凸包中不作为顶点出现，所以此时B点需要删除。

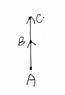
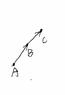
  eg.从最左开始遍历（垂直坐标轴从下到上）

    t=0，即AB，AC共线，按照遍历顺序，C点一定在A点的垂直上或右方，不会出现反向共线的情况。