2020 Multi-University Training Contest 2
A. Total Eclipse
根据题意,每次要选择一个极大连通块,将里面所有数同时减小,直到最小值变成$0$,然后将变成$0$的点删除,分裂成多个连通块再接着做。
将整个过程倒过来看,变成按照$b$的值从大到小依次加入每个点。加入每个点$x$时遍历与$x$相连的所有边$(x,y)$,如果$y$在$x$之前加入且$x$和$y$不连通则将$x$和$y$合并,并将$y$所在连通块的树根的父亲设为$x$,得到一棵有根树。那么每个点$x$在成为最小值之前已经被做了$b_{father_x}$次操作,所以每个点$x$对答案的贡献为$b_x-b_{father_x}$。
使用并查集支持路径压缩,时间复杂度$O((n+m)\log n)$。
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=100010,M=200010;
int Case,n,m,i,j,x,y,a[N],q[N],g[N],v[M<<1],nxt[M<<1],ed,f[N],fa[N],wake[N];long long ans;
inline void add(int x,int y){v[++ed]=y;nxt[ed]=g[x];g[x]=ed;}
inline bool cmp(int x,int y){return a[x]>a[y];}
int F(int x){return f[x]==x?x:f[x]=F(f[x]);}
int main(){
scanf("%d",&Case);
while(Case--){
scanf("%d%d",&n,&m);
for(ed=0,i=1;i<=n;i++){
scanf("%d",&a[i]);
q[i]=f[i]=i;
g[i]=fa[i]=wake[i]=0;
}
while(m--)scanf("%d%d",&x,&y),add(x,y),add(y,x);
sort(q+1,q+n+1,cmp);
for(i=1;i<=n;i++){
x=q[i];
wake[x]=1;
for(j=g[x];j;j=nxt[j]){
y=v[j];
if(!wake[y])continue;
y=F(y);
if(y==x)continue;
fa[y]=f[y]=x;
}
}
for(ans=0,i=1;i<=n;i++)ans+=a[i]-a[fa[i]];
printf("%lld\n",ans);
}
}
B. Blood Pressure Game
将所有数字从小到大排序得到$b_1,b_2,\dots,b_n$,那么$|a_i-a_j|$等价于排序后某些相邻段的差值$b_k-b_{k-1}$的区间和,可以将$\sum |a_j-a_{j-1}|$表示成$\sum cnt_i(b_i-b_{i-1})$,即考虑每对排序后相邻的数$(b_{i-1},b_i)$,统计$b_i-b_{i-1}$对最终结果的贡献。
按照$b_1,b_2,\dots,b_n$的顺序依次将每个数字插入到最终的序列中,设$f[i][j][t]$表示考虑了前$i$个数,这$i$个数目前已经形成了$j$个连通块,其中有$t(0\leq t\leq 2)$个数作为$a_1$或$a_n$的前$k$大方案以及对应的方案数,那么初始状态是$f[1][1][0]$($b_1$不作为$a_1$或$a_n$,有一种方案)和$f[1][1][1]$($b_1$作为$a_1$或$a_n$,有两种方案),目标是求出$f[n][1][2]$。
对于$f[i][j][t]$到$f[i+1][][]$的转移,则$b_{i+1}-b_i$对最终结果的贡献是$(2j-t)(b_{i+1}-b_i)$,有以下几种转移:
- 新建一个不含$a_1$和$a_n$连通块,转移到$f[i+1][j+1][t]$,有$j+1-t$种方案。
- 新建一个作为$a_1$或$a_n$连通块,转移到$f[i+1][j+1][t+1]$,有$2-t$种方案。
- 合并两个连通块,转移到$f[i+1][j-1][t]$,有$j-1$种方案。
- 在某个连通块左侧或右侧扩展,且不作为$a_1$和$a_n$,转移到$f[i+1][j][t]$,有$2j-t$种方案。
- 在某个连通块左侧或右侧扩展,且作为$a_1$或$a_n$,转移到$f[i+1][j][t+1]$,有$2-t$种方案。
对于每个状态,收集到所有转移后,将贡献相同的方案合并,然后保留前$k$大即可,使用快速排序的时间复杂度为$O(n^2k\log k)$,使用归并的时间复杂度为$O(n^2k)$。
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=605,K=25,P=1000000007;
int Case,n,m,o,i,j,k,t,a[N];
struct E{
int x,y;
E(){}
E(int _x,int _y){x=_x,y=_y;}
};
inline bool cmp(const E&a,const E&b){return a.x>b.x;}
struct Info{
int cnt;E v[K*5];
void clr(){cnt=0;}
void add(int A,int B){v[++cnt]=E(A,B);}
void fix(){
sort(v+1,v+cnt+1,cmp);
int i,j,k=0;
for(i=1;i<=cnt;i=j){
int tmp=0;
for(j=i;j<=cnt&&v[i].x==v[j].x;j++)tmp=(tmp+v[j].y)%P;
v[++k]=E(v[i].x,tmp);
if(k>=m)break;
}
cnt=k;
}
}f[2][N][3];
int main(){
scanf("%d",&Case);
while(Case--){
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)scanf("%d",&a[i]);
sort(a+1,a+n+1);
for(i=0;i<2;i++)for(j=0;j<=n;j++)for(k=0;k<3;k++)f[i][j][k].clr();
f[1][1][0].add(0,1);
f[1][1][1].add(0,2);
for(i=o=1;i<n;i++,o^=1){
for(j=0;j<=n;j++)for(k=0;k<3;k++)f[o^1][j][k].clr();
for(j=0;j<=n;j++)for(k=0;k<3;k++){
f[o][j][k].fix();
int cnt=f[o][j][k].cnt;
if(!cnt)continue;
int base=(a[i+1]-a[i])*(j*2-k);
for(t=1;t<=cnt;t++){
int A=base+f[o][j][k].v[t].x,B=f[o][j][k].v[t].y;
if(j+1>k)f[o^1][j+1][k].add(A,1LL*B*(j+1-k)%P);
if(j>1)f[o^1][j-1][k].add(A,1LL*B*(j-1)%P);
if(j*2>k)f[o^1][j][k].add(A,1LL*B*(j*2-k)%P);
if(k<2){
f[o^1][j+1][k+1].add(A,1LL*B*(2-k)%P);
f[o^1][j][k+1].add(A,1LL*B*(2-k)%P);
}
}
}
}
f[o][1][2].fix();
for(i=1;i<=f[o][1][2].cnt&&i<=m;i++)printf("%d %d\n",f[o][1][2].v[i].x,(f[o][1][2].v[i].y%P+P)%P);
for(;i<=m;i++)puts("-1");
}
}
C. Count on a Tree II Striking Back
$k$个$[0,1]$的随机实数的最小值的期望为$\frac{1}{k+1}$。对于一个大小为$k$的集合,如果给每个元素随机一个正整数,那么多次采样得到的平均最小值越小就说明$k$的值越大。
回到本题,进行$k$次采样,每次采样时对每种颜色随机一个正整数,令每个点的点权为其颜色对应的随机数,然后统计询问的树链上点权的最小值,将$k$次采样的结果相加以粗略比较两条树链的颜色数的大小,因为不要求精确值所以$k$取几十即可得到正确结果。
使用树链剖分+线段树的时间复杂度为$O(nk+mk\log^2n)$,使用全局平衡二叉树可以做到$O(nk+mk\log n)$。
#include<cstdio>
#include<algorithm>
using namespace std;
typedef unsigned int U;
typedef long long ll;
const int N=500010,K=30;
const U inf=~0U;
int Case,n,m,i,j,last,op,x,y,A,B,C,D,col[N],g[N],v[N<<1],nxt[N<<1],ed;
int f[N],d[N],size[N],son[N],top[N],loc[N],q[N],dfn;
U w[N][K],val[1111111][K],tmp[K];
U SX=335634763,SY=873658265,SZ=192849106,SW=746126501;
inline U xorshift128(){
U t=SX^(SX<<11);
SX=SY;
SY=SZ;
SZ=SW;
return SW=SW^(SW>>19)^t^(t>>8);
}
inline void add(int x,int y){v[++ed]=y;nxt[ed]=g[x];g[x]=ed;}
void dfs1(int x,int y){
f[x]=y,d[x]=d[y]+1,size[x]=1;
for(int i=g[x];i;i=nxt[i]){
int u=v[i];
if(u==y)continue;
dfs1(u,x);
size[x]+=size[u];
if(size[u]>size[son[x]])son[x]=u;
}
}
void dfs2(int x,int y){
q[loc[x]=++dfn]=x;
top[x]=y;
if(son[x])dfs2(son[x],y);
for(int i=g[x];i;i=nxt[i])if(v[i]!=f[x]&&v[i]!=son[x])dfs2(v[i],v[i]);
}
inline void up(int x){for(int i=0;i<K;i++)val[x][i]=min(val[x<<1][i],val[x<<1|1][i]);}
void build(int x,int a,int b){
if(a==b){
int o=col[q[a]];
for(int i=0;i<K;i++)val[x][i]=w[o][i];
return;
}
int mid=(a+b)>>1;
build(x<<1,a,mid),build(x<<1|1,mid+1,b);
up(x);
}
void change(int x,int a,int b,int c,int p){
if(a==b){
for(int i=0;i<K;i++)val[x][i]=w[p][i];
return;
}
int mid=(a+b)>>1;
if(c<=mid)change(x<<1,a,mid,c,p);else change(x<<1|1,mid+1,b,c,p);
up(x);
}
inline void umin(U&a,U b){a>b?(a=b):0;}
void ask(int x,int a,int b,int c,int d){
if(c<=a&&b<=d){
for(int i=0;i<K;i++)umin(tmp[i],val[x][i]);
return;
}
int mid=(a+b)>>1;
if(c<=mid)ask(x<<1,a,mid,c,d);
if(d>mid)ask(x<<1|1,mid+1,b,c,d);
}
inline ll estimate(int x,int y){
for(int i=0;i<K;i++)tmp[i]=inf;
for(;top[x]!=top[y];x=f[top[x]]){
if(d[top[x]]<d[top[y]])swap(x,y);
ask(1,1,n,loc[top[x]],loc[x]);
}
if(d[x]<d[y])swap(x,y);
ask(1,1,n,loc[y],loc[x]);
ll ret=0;
for(int i=0;i<K;i++)ret+=tmp[i];
return ret;
}
int main(){
for(i=1;i<N;i++)for(j=0;j<K;j++)w[i][j]=xorshift128();
scanf("%d",&Case);
while(Case--){
scanf("%d%d",&n,&m);
for(ed=dfn=last=i=0;i<=n;i++)g[i]=f[i]=d[i]=size[i]=son[i]=0;
for(i=1;i<=n;i++)scanf("%d",&col[i]);
for(i=1;i<n;i++)scanf("%d%d",&x,&y),add(x,y),add(y,x);
dfs1(1,0);
dfs2(1,1);
build(1,1,n);
while(m--){
scanf("%d%d%d",&op,&A,&B);
A^=last,B^=last;
if(op==1)change(1,1,n,loc[A],B);
else{
scanf("%d%d",&C,&D);
C^=last,D^=last;
ll E=estimate(A,B),F=estimate(C,D);
//printf(">> %.15f %.15f\n",(((double)(1ULL<<32))*K)/E-1,(((double)(1ULL<<32))*K)/F-1);
if(E<F){
puts("Yes");
last++;
}else puts("No");
}
}
}
}
D. Diamond Rush
如下图所示,令左上角为起点,右下角为终点,灰色部分为不可走的区域,那么任意一条合法路线必定经过了至少一个红点或绿点。
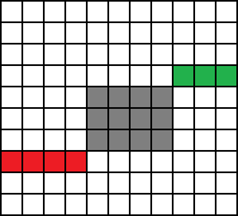
DP出起点到每个点的最长路径、终点到每个点的最长路径,相加以得到经过每个点的最长路径$f[i][j]$,再预处理每一行的前后缀$f$的最大值,则每个询问可以$O(1)$回答。
最后的问题是如何处理权值非常大的情况。对于任意一个方案,令$cnt_i$表示该方案中经过了多少个权值为$\left(n^2\right)^i$的点,则比较两个方案的大小等价于比较字符串$cnt_{n^2},cnt_{n^2-1},\dots,cnt_1$的字典序大小。注意到DP的时候每个DP值对应的方案只会在之前某个DP值对应的方案中将某个$cnt$增加$1$,于是可以用可持久化线段树来记录$cnt$数组,并维护区间Hash值用于$O(\log n)$比较大小。
时间复杂度$O((n^2+q)\log n)$。
#include<cstdio>
typedef unsigned int U;
typedef unsigned long long ull;
const int N=405,M=7000005,P=1000000007;
int Case,n,m,lim,i,j,p[N*N],a[N][N],f[N][N],g[N][N],h[N][N],pre[N][N],suf[N][N];
int tot,l[M],r[M],sum[M],val[M];ull sw[M],weight[N*N];
U SX=335634763,SY=873658265,SZ=192849106,SW=746126501;
inline ull xorshift128(){
U t=SX^(SX<<11);
SX=SY;
SY=SZ;
SZ=SW;
return SW=SW^(SW>>19)^t^(t>>8);
}
inline ull myrand(){return (xorshift128()<<32)^xorshift128();}
int ins(int x,int a,int b,int c){
int y=++tot;
val[y]=val[x]+1;
sum[y]=(sum[x]+p[c])%P;
sw[y]=sw[x]+weight[c];
if(a==b)return y;
int mid=(a+b)>>1;
if(c<=mid)l[y]=ins(l[x],a,mid,c),r[y]=r[x];
else l[y]=l[x],r[y]=ins(r[x],mid+1,b,c);
return y;
}
inline bool bigger(int A,int B,int C,int D){
if(sw[A]+sw[B]==sw[C]+sw[D])return 0;
int a=1,b=lim,mid;
while(a<b){
mid=(a+b)>>1;
if(sw[r[A]]+sw[r[B]]==sw[r[C]]+sw[r[D]]){
b=mid;
A=l[A];
B=l[B];
C=l[C];
D=l[D];
}else{
a=mid+1;
A=r[A];
B=r[B];
C=r[C];
D=r[D];
}
}
return val[A]+val[B]>val[C]+val[D];
}
inline int getmax(int x,int y){
if(!x||!y)return x+y;
return bigger(f[x>>9][x&511],h[x>>9][x&511],f[y>>9][y&511],h[y>>9][y&511])?x:y;
}
int main(){
scanf("%d",&Case);
while(Case--){
scanf("%d%d",&n,&m);
lim=n*n;
for(i=1;i<=lim;i++)weight[i]=myrand();
for(p[0]=i=1;i<=lim;i++)p[i]=1LL*p[i-1]*n%P*n%P;
for(i=1;i<=n;i++)for(j=1;j<=n;j++)scanf("%d",&a[i][j]);
for(i=0;i<=n+1;i++)for(j=0;j<=n+1;j++)f[i][j]=g[i][j]=h[i][j]=pre[i][j]=suf[i][j]=0;
for(i=1;i<=n;i++)for(j=1;j<=n;j++){
f[i][j]=bigger(f[i-1][j],0,f[i][j-1],0)?f[i-1][j]:f[i][j-1];
f[i][j]=ins(f[i][j],1,lim,a[i][j]);
}
for(i=n;i;i--)for(j=n;j;j--){
h[i][j]=bigger(g[i+1][j],0,g[i][j+1],0)?g[i+1][j]:g[i][j+1];
g[i][j]=ins(h[i][j],1,lim,a[i][j]);
}
for(i=1;i<=n;i++)for(j=1;j<=n;j++)pre[i][j]=getmax(pre[i][j-1],i<<9|j);
for(i=n;i;i--)for(j=n;j;j--)suf[i][j]=getmax(suf[i][j+1],i<<9|j);
while(m--){
int xl,xr,yl,yr,ans;
scanf("%d%d%d%d",&xl,&xr,&yl,&yr);
ans=getmax(pre[xr+1][yl-1],suf[xl-1][yr+1]);
printf("%d\n",(sum[f[ans>>9][ans&511]]+sum[h[ans>>9][ans&511]])%P);
}
for(i=0;i<=tot;i++)l[i]=r[i]=sum[i]=val[i]=sw[i]=0;
tot=0;
}
}
E. New Equipments
对于每个二次函数$a_i\times j^2+b_i\times j+c_i$,根据函数性质以及公式找到它在$[1,m]$中的最小值,并在最小值附近找到前$n$小的值,由工人$i$向这$n$个位置连边,则可以建出一张点数边数均为$O(n^2)$的费用流图,然后直接增广$n$次找到流量$=1,2,\dots,n$的最小费用流即可。因为左边任何一个大小为$k(1\leq k\leq n)$的子集都与右边至少$n\geq k$个点相连,所以根据Hall定理一定存在完美匹配,又因为每个点都保留了最小的$n$个取值,所以一定可以找到最优解。
朴素SPFA实现的时间复杂度为$O(n^5)$,常数很小,使用Dijkstra费用流的时间复杂度为$O(n^3\log n)$。
#include<cstdio>
#include<set>
#include<map>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=55,M=N*N+N+7,E=500005;
const ll inf=~0ULL>>1;
int Case,n,m,cnt,i,x,val[N*N];ll a[N],b[N],_c[N],ans;
set<int>all,which[N];
map<int,int>id;
int u[E],v[E],c[E],nxt[E];ll co[E];
int t,S,T,l,r,q[E],g[M],f[M];ll d[M];bool in[M];
inline ll cal(ll a,ll b,ll x){return a*x*x+b*x;}
inline set<int> extend(ll a,ll b){
ll tmp=-(b/(a*2));
tmp-=9;
tmp=max(tmp,1LL);
tmp=min(tmp,1LL*m);
while(tmp<m&&cal(a,b,tmp)>cal(a,b,tmp+1))tmp++;
ll l=tmp,r=tmp+1;
set<int>ret;
ret.clear();
for(int i=1;i<=n;i++){
if(l<1){
ret.insert(r++);
continue;
}
if(r>m){
ret.insert(l--);
continue;
}
if(cal(a,b,l)<cal(a,b,r))ret.insert(l--);else ret.insert(r++);
}
for(set<int>::iterator it=ret.begin();it!=ret.end();it++)all.insert(*it);
return ret;
}
inline void add(int x,int y,int z,ll zo){
u[++t]=x;v[t]=y;c[t]=z;co[t]=zo;nxt[t]=g[x];g[x]=t;
u[++t]=y;v[t]=x;c[t]=0;co[t]=-zo;nxt[t]=g[y];g[y]=t;
}
inline void spfa(){
int x,i;
for(i=1;i<=T;i++)d[i]=inf,in[i]=0;
d[S]=0;in[S]=1;l=r=E>>1;q[l]=S;
while(l<=r){
x=q[l++];
if(x==T)continue;
for(i=g[x];i;i=nxt[i])if(c[i]&&co[i]+d[x]<d[v[i]]){
d[v[i]]=co[i]+d[x],f[v[i]]=i;
if(!in[v[i]]){
in[v[i]]=1;
if(d[v[i]]<d[q[l]])q[--l]=v[i];else q[++r]=v[i];
}
}
in[x]=0;
}
}
int main(){
scanf("%d",&Case);
while(Case--){
scanf("%d%d",&n,&m);
all.clear();
id.clear();
for(i=1;i<=n;i++){
scanf("%lld%lld%lld",&a[i],&b[i],&_c[i]);
which[i]=extend(a[i],b[i]);
}
cnt=0;
for(set<int>::iterator it=all.begin();it!=all.end();it++){
val[++cnt]=*it;
id[*it]=cnt;
}
S=0,T=n+cnt+1;
for(i=0,t=1;i<=T;i++)g[i]=0;
for(i=1;i<=n;i++)add(S,i,1,0);
for(i=1;i<=cnt;i++)add(n+i,T,1,0);
for(i=1;i<=n;i++)for(set<int>::iterator it=which[i].begin();it!=which[i].end();it++)add(i,n+id[*it],1,cal(a[i],b[i],*it)+_c[i]);
ans=0;
for(i=1;i<=n;i++){
spfa();
ans+=d[T];
printf("%lld%c",ans,i<n?' ':'\n');
for(x=T;x!=S;x=u[f[x]])c[f[x]]--,c[f[x]^1]++;
}
}
}
F. The Oculus
令修改的那一位为$k$,则要找到这个$k$满足$A\times B=C+F_k$,其中$k\leq 2000001$。假设存在一个$P$满足$F_1,F_2,\dots,F_{2000001}$模$P$两两不同余,则可以根据$F_k\bmod P=(A\times B-C)\bmod P$得到$k$。事实上取$P=2^{64}$,即自然溢出就是满足条件的。
#include<cstdio>
typedef unsigned long long ull;
const int N=3000005;
int Case,i;ull A,B,C,f[N];
inline ull read(){
int n,i,x;ull ret=0;
scanf("%d",&n);
for(i=1;i<=n;i++){
scanf("%d",&x);
if(x)ret+=f[i];
}
return ret;
}
int main(){
for(f[1]=1,f[2]=2,i=3;i<N;i++)f[i]=f[i-1]+f[i-2];
scanf("%d",&Case);
while(Case--){
A=read();
B=read();
C=read();
A*=B;
for(i=1;C+f[i]!=A;i++);
printf("%d\n",i);
}
}
G. In Search of Gold
二分答案,判断是否存在树直径长度不超过$mid$的方案。
考虑树DP,设$f[i][j]$表示考虑了$i$的子树,其中有$j$条边的取值来自$a$数组的所有树直径$\leq mid$的方案中,与$i$点距离最远的点到$i$的距离的最小可能值。转移时合并之前已经DP过的部分和新加入的子树,如果两部分到$i$的最长距离之和超过$mid$则不转移,因为这表示树直径超过了$mid$。
在转移时加上$j\leq\min(k,size[i])$的剪枝,时间复杂度为$O(nk\log ans)$。
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=20005,M=25;
int Case,n,m,i,x,y,A,B,g[N],v[N<<1],a[N<<1],b[N<<1],nxt[N<<1],ed,size[N];
ll f[N][M],h[N],l,r,mid,ans;
inline void up(ll&a,ll b){a>b?(a=b):0;}
void dfs(int x,int y){
size[x]=f[x][0]=0;
for(int i=g[x];i;i=nxt[i]){
int u=v[i];
if(u==y)continue;
dfs(u,x);
int A=a[i],B=b[i],pre=size[x],cur=size[u],now=min(pre+cur+1,m);
for(int j=0;j<=now;j++)h[j]=mid+1;
for(int j=0;j<=pre;j++)for(int k=0;k<=cur&&j+k<=m;k++){
if(f[x][j]+f[u][k]+A<=mid)up(h[j+k+1],max(f[x][j],f[u][k]+A));
if(f[x][j]+f[u][k]+B<=mid)up(h[j+k],max(f[x][j],f[u][k]+B));
}
size[x]=now;
for(int j=0;j<=now;j++)f[x][j]=h[j];
}
}
int main(){
scanf("%d",&Case);
while(Case--){
scanf("%d%d",&n,&m);
l=r=0;
for(ed=i=0;i<=n;i++)g[i]=0;
for(i=1;i<n;i++){
scanf("%d%d%d%d",&x,&y,&A,&B);
v[++ed]=y;a[ed]=A;b[ed]=B;nxt[ed]=g[x];g[x]=ed;
v[++ed]=x;a[ed]=A;b[ed]=B;nxt[ed]=g[y];g[y]=ed;
r+=max(A,B);
}
while(l<=r){
mid=(l+r)>>1;
dfs(1,0);
if(f[1][m]<=mid)r=(ans=mid)-1;else l=mid+1;
}
printf("%lld\n",ans);
}
}
H. Dynamic Convex Hull
考虑离线对操作序列按时间建立线段树,那么每个函数在时间轴上存在的部分一定是一个区间,将其作为标记插入线段树的$O(\log m)$个节点中;对于每个询问,其在时间轴上对应一个点,那么它的答案对应的函数一定在线段树对应叶子节点到根这$O(\log m)$个节点的标记之中,将其作为询问插入对应的$O(\log m)$个节点中。
那么对于线段树的每个节点,它有若干标记和若干询问,这是一个静态的问题,对于每个询问$x$,分别找到$a_i\leq x$和$a_i\geq x$的最优函数即可。
以$a_i\leq x$为例,考虑两个函数$(x-a_i)^4+b_i$以及$(x-a_j)^4+b_j$,其中$a_i\leq a_j$。如果$i$不比$j$优,则说明$(x-a_i)^4+b_i\geq (x-a_j)^4+b_j$,随着$x$的增大这个不等式将会一直成立,所以将函数按照$a$从小到大排序、将询问按照$x$从小到大排序,则最优决策具有单调性,可以分治求解。
时间复杂度$O((n+m)\log^2m)$。
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=200010,M=262157,K=N*21;
const ll inf=~0ULL>>1;
int Case,n,m,q,i,x;bool is[N];ll ans[N];
int g[M],G[M],v[K],nxt[K],ed;
int pa[N],pb[N];
struct P{int l,r,a;ll b;}a[N],b[N];
inline bool cmp(const P&a,const P&b){return a.a<b.a;}
void build(int x,int a,int b){
g[x]=G[x]=0;
if(a==b)return;
int mid=(a+b)>>1;
build(x<<1,a,mid),build(x<<1|1,mid+1,b);
}
void insp(int x,int a,int b,int c,int d,int p){
if(c<=a&&b<=d){
v[++ed]=p;nxt[ed]=g[x];g[x]=ed;
return;
}
int mid=(a+b)>>1;
if(c<=mid)insp(x<<1,a,mid,c,d,p);
if(d>mid)insp(x<<1|1,mid+1,b,c,d,p);
}
void insq(int x,int a,int b,int c,int p){
v[++ed]=p;nxt[ed]=G[x];G[x]=ed;
if(a==b)return;
int mid=(a+b)>>1;
if(c<=mid)insq(x<<1,a,mid,c,p);else insq(x<<1|1,mid+1,b,c,p);
}
inline ll four(ll x){return x*x*x*x;}
void solve1(int l,int r,int dl,int dr){
int m=(l+r)>>1,dm=dl,x=b[pb[m]].a;ll tmp=inf;
for(int i=dl;i<=dr&&x>=a[pa[i]].a;i++){
ll now=four(x-a[pa[i]].a)+a[pa[i]].b;
if(now<tmp)tmp=now,dm=i;
}
if(tmp<ans[b[pb[m]].l])ans[b[pb[m]].l]=tmp;
if(l<m)solve1(l,m-1,dl,dm);
if(r>m)solve1(m+1,r,dm,dr);
}
void solve2(int l,int r,int dl,int dr){
int m=(l+r)>>1,dm=dr,x=b[pb[m]].a;ll tmp=inf;
for(int i=dr;i>=dl&&x<=a[pa[i]].a;i--){
ll now=four(x-a[pa[i]].a)+a[pa[i]].b;
if(now<tmp)tmp=now,dm=i;
}
if(tmp<ans[b[pb[m]].l])ans[b[pb[m]].l]=tmp;
if(l<m)solve2(l,m-1,dl,dm);
if(r>m)solve2(m+1,r,dm,dr);
}
inline void work(int g,int G){
int ca=0,cb=0,i;
for(;g;g=nxt[g])pa[++ca]=v[g];
for(;G;G=nxt[G])pb[++cb]=v[G];
if(!ca||!cb)return;
for(i=1;i<=cb;i++)if(b[pb[i]].a>=a[pa[1]].a){
solve1(i,cb,1,ca);
break;
}
for(i=cb;i;i--)if(b[pb[i]].a<=a[pa[ca]].a){
solve2(1,i,1,ca);
break;
}
}
void dfs(int x,int a,int b){
work(g[x],G[x]);
if(a==b){
if(is[a]){
if(ans[a]==inf)ans[a]=-1;
printf("%lld\n",ans[a]);
}
return;
}
int mid=(a+b)>>1;
dfs(x<<1,a,mid);
dfs(x<<1|1,mid+1,b);
}
int main(){
scanf("%d",&Case);
while(Case--){
scanf("%d%d",&n,&m);
q=ed=0;
for(i=1;i<=n;i++){
scanf("%d%lld",&a[i].a,&a[i].b);
a[i].l=1,a[i].r=m;
}
for(i=1;i<=m;i++){
int op;
scanf("%d",&op);
is[i]=op==3;
ans[i]=inf;
if(op==1){
n++;
scanf("%d%lld",&a[n].a,&a[n].b);
a[n].l=i,a[n].r=m;
}else if(op==2){
scanf("%d",&x);
a[x].r=i;
}else{
q++;
scanf("%d",&b[q].a);
b[q].l=i;
}
}
sort(a+1,a+n+1,cmp);
sort(b+1,b+q+1,cmp);
build(1,1,m);
for(i=n;i;i--)insp(1,1,m,a[i].l,a[i].r,i);
for(i=q;i;i--)insq(1,1,m,b[i].l,i);
dfs(1,1,m);
}
}
I. It's All Squares
对于每个询问,求出经过的点的横纵坐标的最小值和最大值,显然可以只在框出的矩形里做。在框出的矩形里递推出每个点往左边射线会经过多少次多边形的边界,则根据这个值的奇偶性可以判断出每个点是否在多边形里从而得到答案。
不妨设$n,m$同阶,当询问的形状是正方形时该算法的时间复杂度最大,令正方形的边长为$k(k\leq n)$,则消耗$4k$的输入量需要支付$O(k^2)$的时间。所以最坏情况下需要支付$O(\frac{\sum|S|n}{4})$的时间,这个值只有$10^8$左右,所以可以接受。
#include<cstdio>
#include<cstring>
const int N=405,M=4000005;
int Case,n,m,q,i,j,o,x,y,sx,sy,xl,xr,yl,yr,len,a[N][N],v[N*N],POS,ans;
bool tag[N][N];
char op[M];
inline void umin(int&a,int b){a>b?(a=b):0;}
inline void umax(int&a,int b){a<b?(a=b):0;}
int main(){
scanf("%d",&Case);
while(Case--){
scanf("%d%d%d",&n,&m,&q);
for(i=1;i<=n;i++)for(j=1;j<=m;j++)scanf("%d",&a[i][j]);
while(q--){
scanf("%d%d%s",&sx,&sy,op);
len=strlen(op);
xl=n,xr=0,yl=m,yr=0;
for(x=sx,y=sy,i=0;i<len;i++){
umin(xl,x);
umax(xr,x);
umin(yl,y);
umax(yr,y);
if(op[i]=='L')x--;
if(op[i]=='R')x++;
if(op[i]=='D')y--;
if(op[i]=='U')y++;
}
xl++,yl++;
for(i=xl;i<=xr;i++)for(j=yl;j<=yr;j++)tag[i][j]=0;
for(x=sx,y=sy,i=0;i<len;i++){
if(op[i]=='L'){
tag[x][y+1]^=1;
x--;
}
if(op[i]=='R'){
x++;
tag[x][y+1]^=1;
}
if(op[i]=='D')y--;
if(op[i]=='U')y++;
}
POS++;
ans=0;
for(i=xl;i<=xr;i++)for(o=0,j=yl;j<=yr;j++){
o^=tag[i][j];
if(!o)continue;
if(v[a[i][j]]!=POS)v[a[i][j]]=POS,ans++;
}
printf("%d\n",ans);
}
}
}
J. Lead of Wisdom
令第$i$种装备的数量为$cnt_i$,显然如果$cnt_i$不为$0$那么这一种装备不空的方案一定比空的方案优,在这时需要考虑的总方案数为$\prod\max(cnt_i,1)$,其中$\sum cnt_i\leq 50$。最坏情况下所有$cnt$的值都相同,令它们都等于$k$,则方案数为$k^{\frac{n}{k}}$,当$k$取$3$时取到最大值$3^{\frac{n}{3}}$,在$n=50$时并不算太大,因此可以直接爆搜所有方案得到最优解。
需要注意的是,$cnt_i=0$的部分应该直接跳过,以保证搜索树上每一层的节点数至少是上一层的两倍,使得时间复杂度为$O(3^{\frac{n}{3}})$,否则会退化成$O(n3^{\frac{n}{3}})$而TLE。
#include<cstdio>
typedef long long ll;
const int N=55;
int Case,n,m,i,j,x,cnt[N],nxt[N],e[N][N][4];ll ans;
void dfs(int x,int a,int b,int c,int d){
if(x>m){
ll tmp=1LL*a*b*c*d;
if(tmp>ans)ans=tmp;
return;
}
int num=cnt[x];
if(!num){
dfs(nxt[x],a,b,c,d);
return;
}
for(int i=1;i<=num;i++)dfs(x+1,a+e[x][i][0],b+e[x][i][1],c+e[x][i][2],d+e[x][i][3]);
}
int main(){
scanf("%d",&Case);
while(Case--){
scanf("%d%d",&n,&m);
for(i=1;i<=m;i++)cnt[i]=0;
while(n--){
scanf("%d",&x);
cnt[x]++;
for(j=0;j<4;j++)scanf("%d",&e[x][cnt[x]][j]);
}
x=m+1;
for(i=m;i;i--){
nxt[i]=x;
if(cnt[i])x=i;
}
ans=0;
dfs(1,100,100,100,100);
printf("%lld\n",ans);
}
}
K. King of Hot Pot
首先可以发现最优解可以增量构造,即往吃$k$份肉的最优解加入一份肉可以得到吃$k+1$份肉的最优解,因此存在一个顺序$ord_1,ord_2,\dots,ord_n$满足$ord_1,ord_2,\dots,ord_k$是吃$k$份肉的一个最优解吃的肉对应的集合。
假设确定了要吃哪些肉,那么肯定是按照捞出锅的时间从小到大吃。按照出锅时间从小到大依次考虑每份肉,在$ord_1,ord_2,\dots,ord_{i-1}$中找到一个位置插入第$i$ 份肉。令第$i$份肉的出锅时间为$a$,吃掉它的时间为$b$,设$ord_1,ord_2,\dots,ord_{i-1}$里按照出锅时间顺序吃掉前$k$份肉$ord_1,ord_2,\dots,ord_k$所需的时间为$t_k$,则将$ord_k$替换成第$i$份肉后,对应的方案所需的时间为$\max(t_{k-1},a)+b$,如果$\max(t_{k-1},a)+b<t_k$,则第$i$份肉应该插在$ord_k$ 之前。注意到满足条件的$k$是$ord$序列的一个后缀,所以可以二分找到对应的位置,将第$i$份肉插入$ord$序列,并将后面部分的$t$都修正为$\max(t,a)+b$。
为了加速这个过程,可以用平衡树维护$ord$序列,每个位置记录$t_k$以及$t_{k-1}$方便二分,在修正$t$为$\max(t,a)+b$时,根据$t$的单调性将$t$的一个区间赋值为$a$,再将一个后缀加上$b$。最后得到的$t$序列就是答案。
时间复杂度$O(n\log n)$。
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=300010;
int Case,n,i;
struct E{ll ok,eat;}a[N];
inline bool cmp(const E&a,const E&b){return a.ok<b.ok;}
int root,f[N],son[N][2];
int tagpc[N],tagcc[N];
ll tagpa[N],tagca[N],pre[N],cur[N];
int cnt,q[N];ll ans[N];
inline void tagpre(int x,int c,ll a){
if(!x)return;
pre[x]=pre[x]*c+a;
tagpc[x]*=c;
tagpa[x]=tagpa[x]*c+a;
}
inline void tagcur(int x,int c,ll a){
if(!x)return;
cur[x]=cur[x]*c+a;
tagcc[x]*=c;
tagca[x]=tagca[x]*c+a;
}
inline void push(int x){
if(tagpc[x]!=1||tagpa[x]){
tagpre(son[x][0],tagpc[x],tagpa[x]);
tagpre(son[x][1],tagpc[x],tagpa[x]);
tagpc[x]=1;
tagpa[x]=0;
}
if(tagcc[x]!=1||tagca[x]){
tagcur(son[x][0],tagcc[x],tagca[x]);
tagcur(son[x][1],tagcc[x],tagca[x]);
tagcc[x]=1;
tagca[x]=0;
}
}
inline void rotate(int x){
int y=f[x],w=son[y][1]==x;
son[y][w]=son[x][w^1];
if(son[x][w^1])f[son[x][w^1]]=y;
if(f[y]){
int z=f[y];
if(son[z][0]==y)son[z][0]=x;
if(son[z][1]==y)son[z][1]=x;
}
f[x]=f[y];son[x][w^1]=y;f[y]=x;
}
inline void splay(int x,int o){
while(f[x]!=o){
int y=f[x];
if(f[y]!=o){if((son[f[y]][0]==y)^(son[y][0]==x))rotate(x);else rotate(y);}
rotate(x);
}
if(!o)root=x;
}
inline void insert(int x){
int y=root,nxt=0,last=root;
while(y){
last=y;
push(y);
if(max(pre[y],a[x].ok)+a[x].eat<cur[y]){
nxt=y;
y=son[y][0];
}else{
y=son[y][1];
}
}
splay(last,0);
if(!nxt){
son[x][0]=last;
f[last]=x;
pre[x]=cur[last];
cur[x]=max(pre[x],a[x].ok)+a[x].eat;
root=x;
return;
}
splay(nxt,0);
pre[x]=pre[nxt];
cur[x]=max(pre[x],a[x].ok)+a[x].eat;
int tmp=son[nxt][0];
son[x][0]=tmp;
son[nxt][0]=0;
if(tmp)f[tmp]=x;
son[x][1]=nxt;
f[nxt]=x;
root=x;
pre[nxt]=cur[x];
cur[nxt]=max(cur[nxt],a[x].ok)+a[x].eat;
y=son[nxt][1];
if(!y)return;
int z=0;
last=y;
while(y){
last=y;
push(y);
if(cur[y]<a[x].ok){
z=y;
y=son[y][1];
}else{
y=son[y][0];
}
}
splay(last,nxt);
if(!z){
tagcur(last,1,a[x].eat);
tagpre(son[last][1],1,a[x].eat);
pre[last]=cur[nxt];
return;
}
splay(z,nxt);
tagcur(son[z][0],0,a[x].ok+a[x].eat);
tagcur(son[z][1],1,a[x].eat);
cur[z]=a[x].ok+a[x].eat;
tagpre(son[z][0],0,a[x].ok+a[x].eat);
tagpre(son[z][1],1,a[x].eat);
pre[z]=a[x].ok+a[x].eat;
z=son[z][1];
last=0;
while(z){
last=z;
z=son[z][0];
}
if(last){
splay(last,0);
pre[last]=a[x].ok+a[x].eat;
}
}
void dfs(int x){
if(!x)return;
push(x);
dfs(son[x][0]);
cnt++;
q[cnt]=x;
ans[cnt]=cur[x];
dfs(son[x][1]);
}
int main(){
scanf("%d",&Case);
while(Case--){
scanf("%d",&n);
for(i=1;i<=n;i++)scanf("%lld%lld",&a[i].ok,&a[i].eat);
sort(a+1,a+n+1,cmp);
root=1;
pre[1]=0;
cur[1]=a[1].ok+a[1].eat;
for(i=1;i<=n;i++)tagpc[i]=tagcc[i]=1;
for(i=2;i<=n;i++)insert(i);
dfs(root);
for(i=1;i<=n;i++)printf("%lld%c",ans[i],i<n?' ':'\n');
for(cnt=i=0;i<=n;i++){
f[i]=0;
son[i][0]=son[i][1]=0;
tagpc[i]=tagcc[i]=0;
tagpa[i]=tagca[i]=pre[i]=cur[i]=0;
q[i]=ans[i]=0;
}
}
}
L. String Distance
考虑修改完毕后的$A$串和$B$串,它们对应位置的字符都相等,对于每一位:
- 如果两个串在这一位都做了插入操作,那么可以同时不做插入操作使得操作次数减少$2$。
- 如果一个串$A$在这一位做了插入操作,另一个串$B$这一位不动,那么可以通过$A$这一位不动,$B$删除这一位达到同样的效果。
因此可以发现插入操作是没用的,所以两个串$A$和$B$的距离等于$|A|+|B|-2LCS(A,B)$,其中LCS表示最长公共子序列。预处理出$g[i][j]$表示$A[i..n]$里字符$j$最早出现的下标。对于每个询问通过DP求出LCS,设$f[i][j]$表示与$B[1..i]$的公共序列长度达到$j$的$A[l..r]$的最短前缀的长度,利用$g$数组进行转移。
时间复杂度$O(26n+qm^2)$。
#include<cstdio>
#include<cstring>
const int N=100010,M=25,S=26;
int Case,n,m,q,i,j,l,r,g[N][S],f[M][M];char a[N],b[M];
inline void up(int&a,int b){a>b?(a=b):0;}
inline int cal(int l,int r){
int i,j;
for(i=0;i<=m;i++)for(j=0;j<=i;j++)f[i][j]=N;
f[0][0]=l-1;
for(i=0;i<m;i++)for(j=0;j<=i;j++){
up(f[i+1][j],f[i][j]);
if(f[i][j]<r)up(f[i+1][j+1],g[f[i][j]+1][b[i+1]]);
}
for(i=m;i;i--)for(j=i;j<=m;j++)if(f[j][i]<=r)return i;
return 0;
}
int main(){
scanf("%d",&Case);
while(Case--){
scanf("%s%s",a+1,b+1);
n=strlen(a+1),m=strlen(b+1);
for(i=1;i<=n;i++)a[i]-='a';
for(i=1;i<=m;i++)b[i]-='a';
for(j=0;j<S;j++)g[n+1][j]=n+1;
for(i=n;i;i--){
for(j=0;j<S;j++)g[i][j]=g[i+1][j];
g[i][a[i]]=i;
}
scanf("%d",&q);
while(q--)scanf("%d%d",&l,&r),printf("%d\n",r-l+1+m-2*cal(l,r));
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号