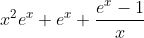求幂级数的和函数出现n的高次方的解决方法
在求解幂级数的和函数时,会遇到下列情况:
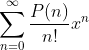
其中P(n)为n的n阶多项式。这种情况可以将P(n)变形,使其可以被消去,从而便于求解。
例:
求幂级数:
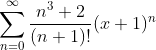
的和函数。
解:
将n^3+2化为(n^3-n)+(n+1)+1,使得原式变形为:
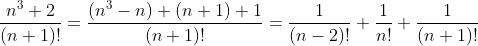
则原级数化为:
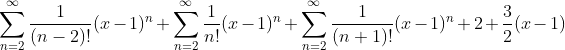
则和函数S(x)为:
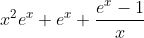
在求解幂级数的和函数时,会遇到下列情况:
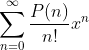
其中P(n)为n的n阶多项式。这种情况可以将P(n)变形,使其可以被消去,从而便于求解。
例:
求幂级数:
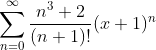
的和函数。
解:
将n^3+2化为(n^3-n)+(n+1)+1,使得原式变形为:
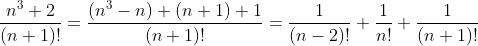
则原级数化为:
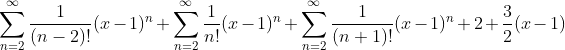
则和函数S(x)为: