求解数列极限的特殊方法

1、当所求极限表达式中出现类似于f(1/n)-f(1/(n+1))元素时，可用拉格朗日中值定理将其转化为f'(t)*(1/n-1/(n+1))(t介于1/n和1/(n+1))之间，以便于计算极限值。

 2、当所求极限为（a1+a2+...+an)/bn的形式时，可用STOLZ定理将其转化为an/(bn-b(n-1))的形式，便于计算（bn满足当n趋于无穷时bn单调递增且发散）。

例：计算极限

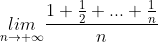
解：由STOLZ定理将原极限转化为

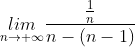
可得原极限值为0。

3、所求极限形式为(an)^(1/n)形式时，可对原式取对数进行转化，转化后进行计算。

4、类似于如下形式的极限（其中Pb(n)为n的b阶多项式，且满足a>b）

可将其转化为

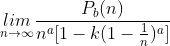
利用等价无穷小替换求解。