Monte Carlo模拟

Monte Carlo模拟

Monte Carlo模拟是人们研究分子体系时出现的第一个计算机模拟方法，名字来源于摩纳哥公国的一座以赌博业闻名的城市Monte Carlo。Monte Carlo模拟以概率和统计理论为基础，使用随机数从\(3N\)维的空间中随机选取构象进行研究。在相空间抽样时，随机产生一个体系的初始构象，按一定的抽样规则生成另一个尝试构象并判断接受或者拒绝尝试构象，进行多次抽样计算可观测量的统计平均值。抽样方法有简单抽样和重要抽样，简单抽样是在相空间中以相同的概率抽取构象得到可观测量的统计平均值。而Metropolis重要性抽样是构造一个带有重要性权重的随机行走，满足细致平衡和各态历经条件，在重要的区域多次取样，抽取构象的分布函数和平衡态构象分布一致，可以有效地得到和温度有关的可观测量的统计平均值。

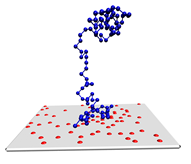
图1 高分子链在非均匀表面的吸附

在分子模拟中，Monte Carlo模拟常常采用Metropolis重要性抽样方法，来研究高分子链在表面的吸附和扩散过程。如图1所示，表面通常是非均匀的[1,2]， 也可以考虑高分子链的刚性的影响[3]。模拟的具体模拟步骤如下：

（1）随机产生一条初始高分子链，生成一个非均匀表面；

（2）随机选择高分子链上的一个链节\(i\)，尝试让链节\(i\)的位置(\(x_i\), \(y_i\), \(z_i\))在\(x\)、\(y\)、\(z\)方向上分别随机改变\(\Delta x\)、\(\Delta y\)、\(\Delta z\)，到达新位置(\(x_i'\), \(y_i'\), \(z_i'\))，产生新的高分子链。如果新位置同时满足是空的、键长合适、键不交叉，就进行（3），否则回到（2）。在三维简立方格点模型中，新位置是在六个最近邻格点中选择。在非格点模型中\(\Delta x\)、\(\Delta y\)、\(\Delta z\)分别在区间[-\(\Delta x\), \(\Delta x\)]、[-\(\Delta y\), \(\Delta y\)]和[-\(\Delta z\), \(\Delta z\)]内，它们的取值要考虑到程序运行的速度，通常在区间\((0.3, 0.5)\)内，模拟时根据具体情况确定取值。

（3）计算新旧构象的能量差\(\Delta E\)，随机生成一个\([0,1)\)区间内的随机数\(p\)，如果\(p\) ≤ \(\min [1, \frac{e^{-\Delta E}}{kBT}]\)，那么接受这次尝试移动，否则回到（2）。

（4）不断重复（2）、（3），直到预先设定的终止条件。模拟的时间单位为Monte Carlo步长（Monte Carlo step，MCS），在一个MCS里每个链节平均移动一次。每隔一段时间（如100MCS），记录可观测量。

（5）重复（1）至（4），模拟不同的样本，计算可观测量的统计平均值。

参考文献：

(1) Yang Qinghui; Qi Hangkai; Yang Xiao; Luo Mengbo*; Simulation study on the critical adsorption and diffusion of polymer chains on heterogeneous surfaces with random adsorption sites, Soft Matter, 2021, 17: 1000.

(2) Yang Qinghui; Yang Xiao; Luo Mengbo*; Adsorption of polymer chains on heterogeneous surfaces with random adsorption sites, Polymer, 2019, 180: 121677.

(3) Yang Xiao; Yang Qinghui; Fu Yu; Wu Fan; Huang Jianhua; Luo Mengbo*; Study on the adsorption process of a semi-flexible polymer onto homogeneous attractive surfaces, Polymer, 2019, 172: 83.