吴恩达机器学习2022 -- Course1 -- Week3(分类问题) - 指南
1. 逻辑回归
1.1 线性回归不适用于分类问题
在监督学习中,我们通常处理两类任务:
- 回归(Regression):预测一个连续值,例如房价
- 分类(Classification):预测一个离散标签,例如判断邮件是否为垃圾邮件
当输出只有两种可能结果时(如“是/否”、“良性/恶性”),这类问题称为二元分类(Binary Classification)。通常用 0 表示负类(如“否”),用 1 表示正类(如“是”)
- 下图为肿瘤二元分类示意图:
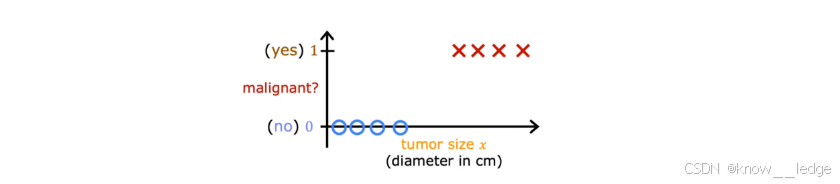
概念明晰:尽管名字叫 “ 逻辑回归 ” ,但它实际上是一个分类算法,而不是回归算法。这是历史命名造成的误解。
为什么不能直接用线性回归解决分类问题?
通过我们能够在上方的肿瘤二元分类示意图上用线性回归拟合一条直线:
f w , b ( x ) = w x + b f_{w,b}(x) = wx + bfw,b(x)=wx+b
然后设定一个阈值(例如 0.5)进行分类:
- 若 f ( x ) < 0.5 f(x) < 0.5f(x)<0.5,预测为 0(良性)
- 若 f ( x ) ≥ 0.5 f(x) \geq 0.5f(x)≥0.5,预测为 1(恶性)
这看起来似乎可行,但存在严重困难
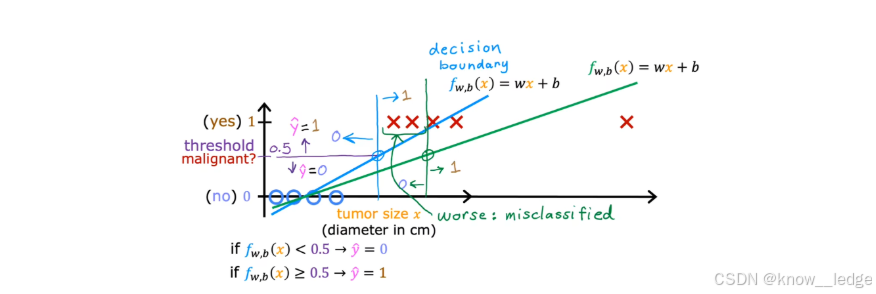
- 问题一:模型输出可能超出 [0, 1] 范围(输出无界)
线性回归的输出是任意实数。例如:
- 当 x = 0 x = 0x=0,f ( x ) = − 1.2 f(x) = -1.2f(x)=−1.2
- 当 x = 10 x = 10x=10,f ( x ) = 3.8 f(x) = 3.8f(x)=3.8
但分类难题中,我们希望输出表示“属于正类的概率”,而概率必须在0 到 1 之间
- 说“恶性概率是“ -1.2 ”或“ 3.8 ”没有意义
- 问题二:对异常值敏感,决策边界不稳定
如果新增一个极端样本(例如一个直径很大的良性肿瘤),线性回归会为了拟合这个点而大幅调整直线斜率,导致原本正确的分类边界被破坏
- 这是因为线性回归的目标是最小化预测值与真实值之间的平方误差,而不是最大化分类准确率
- 因此,我们需要一种专门用于分类的模型——逻辑回归(Logistic Regression)。
1.2 逻辑回归模型
1)Sigmoid 函数
为了解决线性回归输出无界的问题,逻辑回归引入了一个关键函数:Sigmoid 函数(也称为 Logistic 函数)
它的数学表达式为:
g ( z ) = 1 1 + e − z g(z) = \frac{1}{1 + e^{-z}}g(z)=1+e−z1
Sigmoid 函数的特点
- 输入 z zz可能是任意实数(− ∞ < z < + ∞ -\infty < z < +\infty−∞<z<+∞);
- 输出始终在 ( 0 , 1 ) (0, 1)(0,1) 区间内;
- 当 z = 0 z = 0z=0 时,g ( z ) = 0.5 g(z) = 0.5g(z)=0.5;
- 当 z → + ∞ z \to +\inftyz→+∞,g ( z ) → 1 g(z) \to 1g(z)→1;
- 当 z → − ∞ z \to -\inftyz→−∞,g ( z ) → 0 g(z) \to 0g(z)→0。
这使得 Sigmoid 函数非常适合用来表示“概率”。
- 如图为“肿瘤是否恶性”的分类问题(采用 Sigmoid 函数):
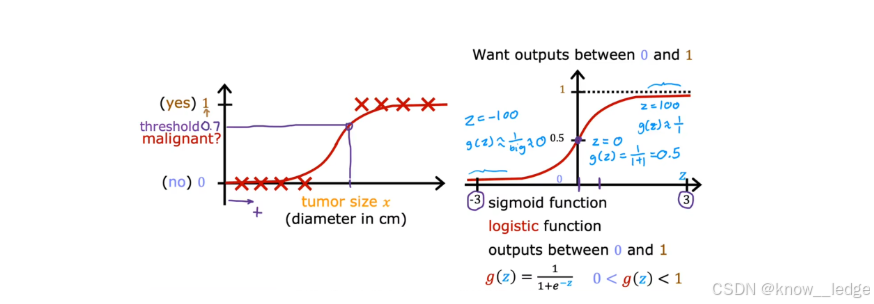
- 如果模型输出为 0.7 → 表示该肿瘤有70% 的可能是恶性;
- 输出为 0.3 → 则表示有 30% 可能是恶性。
2)逻辑回归模型的构建
我们结合线性模型和 Sigmoid 函数,构建完整的逻辑回归模型:
- 线性部分(z):设输入特征向量为x ⃗ \vec{x}x,权重向量为w ⃗ \vec{w}w,偏置项为 b bb,则:
z = w ⃗ ⋅ x ⃗ + b z = \vec{w} \cdot \vec{x} + bz=w⋅x+b
- 这就是大家熟悉的线性组合,可以是单个特征(如肿瘤大小),也可以是多个特征的加权和。
- 通过 Sigmoid 函数转换为概率:将 z zz代入 Sigmoid 函数转换为概率
f w ⃗ , b ( x ⃗ ) = g ( z ) = 1 1 + e − ( w ⃗ ⋅ x ⃗ + b ) f_{\vec{w},b}(\vec{x}) = g(z) = \frac{1}{1 + e^{-(\vec{w} \cdot \vec{x} + b)}}fw,b(x)=g(z)=1+e−(w⋅x+b)1
- 这个输出可以解释为:
在给定特征 x ⃗ \vec{x}x 和参数 w ⃗ , b \vec{w}, bw,b的情况下,样本属于正类(y = 1 y=1y=1)的概率:
- P ( y = 1 ∣ x ⃗ ; w ⃗ , b ) = f w ⃗ , b ( x ⃗ ) P(y=1 \mid \vec{x}; \vec{w}, b) = f_{\vec{w},b}(\vec{x})P(y=1∣x;w,b)=fw,b(x)
1.3 决策边界
决策边界是逻辑回归模型中特别关键的概念:它决定了“什么时候预测为 1,什么时候预测为 0”。
1)什么是决策边界?
一个概率值:就是在逻辑回归中,模型输出的
f w ⃗ , b ( x ⃗ ) = g ( z ) = 1 1 + e − ( w ⃗ ⋅ x ⃗ + b ) f_{\vec{w},b}(\vec{x}) = g(z) = \frac{1}{1 + e^{-(\vec{w} \cdot \vec{x} + b)}}fw,b(x)=g(z)=1+e−(w⋅x+b)1
其中 w ⃗ ⋅ x ⃗ + b \vec{w} \cdot \vec{x} + bw⋅x+b是线性部分,f w ⃗ , b ( x ⃗ ) = g ( z ) f_{\vec{w},b}(\vec{x}) = g(z)fw,b(x)=g(z)表示给定输入x ⃗ \vec{x}x,样本属于正类(标签为 1)的概率。
虽然模型输出的是一个概率值,但分类任务必须明确的类别(0 或 1)。因此引入决策边界(通常为 0.5):
- 若 f w ⃗ , b ( x ⃗ ) ≥ 0.5 f_{\vec{w},b}(\vec{x}) \geq 0.5fw,b(x)≥0.5 → 预测为 1(正类)
- 若 f w ⃗ , b ( x ⃗ ) < 0.5 f_{\vec{w},b}(\vec{x}) < 0.5fw,b(x)<0.5 → 预测为 0(负类)
注意:由于 Sigmoid 函数在z = 0 z = 0z=0时输出 0.5,因此上述规则等价于:
- 若 w ⃗ ⋅ x ⃗ + b ≥ 0 \vec{w} \cdot \vec{x} + b \geq 0w⋅x+b≥0→ 预测为 1
- 若 w ⃗ ⋅ x ⃗ + b < 0 \vec{w} \cdot \vec{x} + b < 0w⋅x+b<0→ 预测为 0
这说明:逻辑回归的决策边界仍然是线性的带有概率意义的预测就是,只是它的输出不再是便捷的 0/1,而
这意味着,决策边界由等式w ⃗ ⋅ x ⃗ + b = 0 \vec{w} \cdot \vec{x} + b = 0w⋅x+b=0 确定。
示例1:决策边界为直线
对于有两个特征x 1 x_1x1 和 x 2 x_2x2的情况,逻辑回归的决策边界由以下方程定义:
w 1 x 1 + w 2 x 2 + b = 0 w_1 x_1 + w_2 x_2 + b = 0w1x1+w2x2+b=0
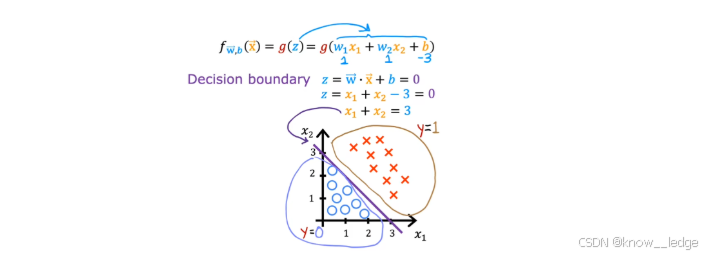
这是一个二维平面上的直线,将样本空间划分为两个区域:
- 直线右侧的点满足w 1 x 1 + w 2 x 2 + b > 0 w_1 x_1 + w_2 x_2 + b > 0w1x1+w2x2+b>0,模型预测为1
- 左侧满足 w 1 x 1 + w 2 x 2 + b < 0 w_1 x_1 + w_2 x_2 + b < 0w1x1+w2x2+b<0,模型预测为0
例如,若 w 1 = 2 w_1 = 2w1=2、w 2 = − 3 w_2 = -3w2=−3、b = 1 b = 1b=1,则决策边界为:
2 x 1 − 3 x 2 + 1 = 0 2x_1 - 3x_2 + 1 = 02x1−3x2+1=0
- 该直线斜率为2 3 \frac{2}{3}32。图中通常用不同颜色或标记(如 ○ 和 ×)表示两类样本,而决策边界正好位于它们之间,实现分类分隔。
示例2:决策边界为圆
曲线。例如,当特征之间存在非线性关系时,我们可以构造一个就是在某些情况下,数据的自然分界不是直线,而非线性决策边界。
本分类疑问中,定义:
z = w 1 x 1 2 + w 2 x 2 2 + b z = w_1 x_1^2 + w_2 x_2^2 + bz=w1x12+w2x22+b
假设参数 w 1 = 1 w_1 = 1w1=1、w 2 = 1 w_2 = 1w2=1、b = − 1 b = -1b=−1,则:
z = x 1 2 + x 2 2 − 1 z = x_1^2 + x_2^2 - 1z=x12+x22−1
决策边界由 g ( z ) = 0.5 g(z) = 0.5g(z)=0.5 决定,即:
x 1 2 + x 2 2 − 1 = 0 ⇒ x 1 2 + x 2 2 = 1 x_1^2 + x_2^2 - 1 = 0 \quad \Rightarrow \quad x_1^2 + x_2^2 = 1x12+x22−1=0⇒x12+x22=1
这是一个以原点为中心、半径为 1 的单位圆。

- 圆内部(x 1 2 + x 2 2 < 1 x_1^2 + x_2^2 < 1x12+x22<1)的点被预测为0(负类);
- 圆外部(x 1 2 + x 2 2 > 1 x_1^2 + x_2^2 > 1x12+x22>1)的点被预测为1(正类);
这说明:线性的就是就算模型本身,但凭借引入特征变换(如平方项),我们可以在原始空间中达成非线性分类。
2. 逻辑回归的代价函数
提示:
log表示以自然常数 e ee 为底的对数(即ln)。
2.1 为什么不启用线性回归的平方误差?
在线性回归中,我们使用均方误差(MSE)作为代价函数:
J ( w , b ) = 1 2 m ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) ) 2 J(w, b) = \frac{1}{2m} \sum_{i=1}^{m} (f_{w,b}(x^{(i)}) - y^{(i)})^2J(w,b)=2m1i=1∑m(fw,b(x(i))−y(i))2
但逻辑回归不能直接用这个公式!原因如下:
逻辑回归的预测值是通过Sigmoid 函数 输出的:
f w , b ( x ) = 1 1 + e − ( w x + b ) f_{w,b}(x) = \frac{1}{1 + e^{-(wx + b)}}fw,b(x)=1+e−(wx+b)1
这是一个非线性、S 形的函数,输出始终在 (0,1) 之间。如果把 Sigmoid 函数代入平方误差公式,得到的代价函数会高度非凸(non-convex),形状像“波浪山”。
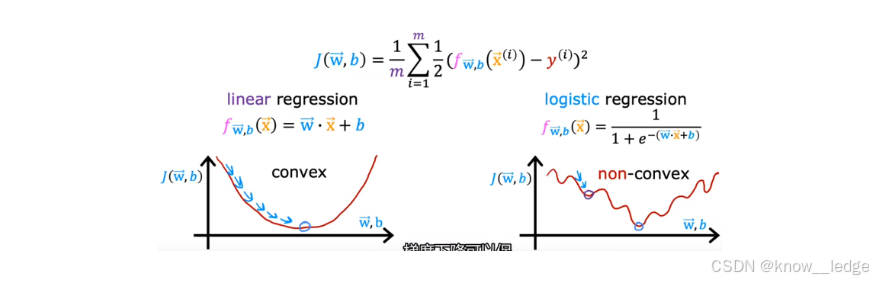
- 非凸函数有多个局部最小值,梯度下降算法很容易卡在某个“假最低点”,无法找到全局最优解。
所以我们需要一个凸函数(convex)的代价函数——只有一个“碗底”,保证梯度下降一定能收敛到最优解。
2.2 逻辑回归的损失函数(单个样本)
逻辑回归要运用一种叫对数损失 的函数
对于单个训练样本( x ( i ) , y ( i ) ) (x^{(i)}, y^{(i)})(x(i),y(i)),其损失函数定义为:
L ( f w , b ( x ( i ) ) , y ( i ) ) = { − log ( f w , b ( x ( i ) ) ) , y ( i ) = 1 − log ( 1 − f w , b ( x ( i ) ) ) , y ( i ) = 0 L(f_{w,b}(x^{(i)}), y^{(i)}) = \begin{cases} -\log(f_{w,b}(x^{(i)})) ,& \text y^{(i)} = 1 \\ -\log(1 - f_{w,b}(x^{(i)})), & \text y^{(i)} = 0 \end{cases}L(fw,b(x(i)),y(i))={−log(fw,b(x(i))),−log(1−fw,b(x(i))),y(i)=1y(i)=0
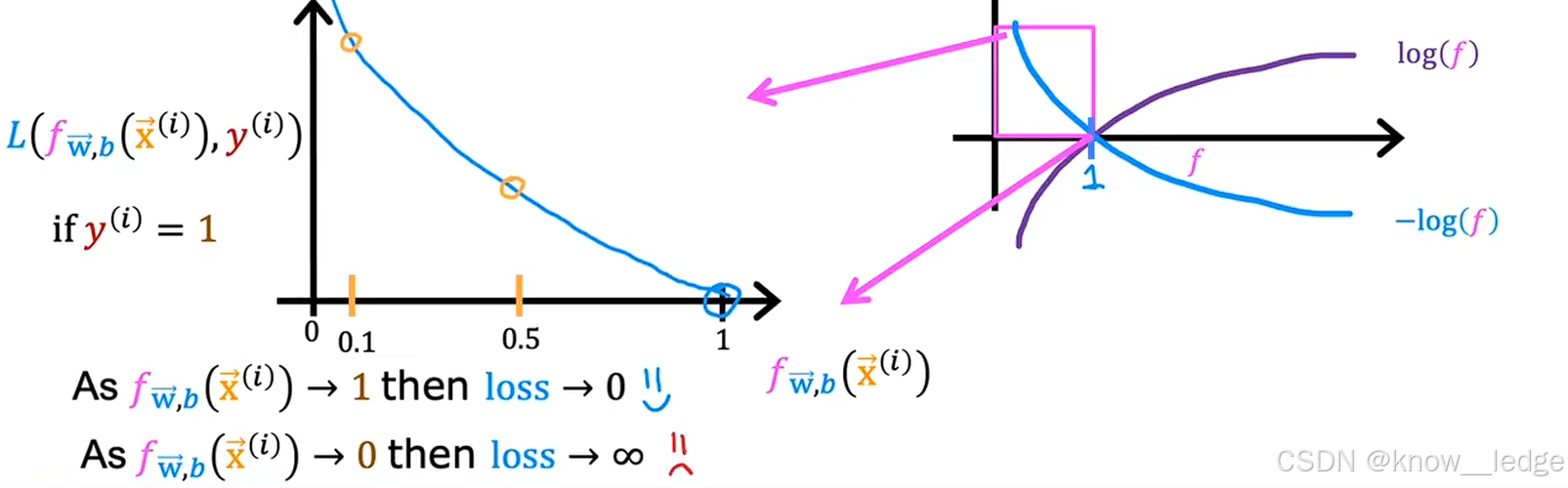
当 y ( i ) = 1 y^{(i)} = 1y(i)=1 时:
- 大家希望预测值f w , b ( x ( i ) ) f_{w,b}(x^{(i)})fw,b(x(i))越接近 1 越好;
- 若 f → 1 f \to 1f→1,则 − log ( f ) → 0 -\log(f) \to 0−log(f)→0→ 损失小;
- 若 f → 0 f \to 0f→0,则 − log ( f ) → + ∞ -\log(f) \to +\infty−log(f)→+∞→ 损失极大。
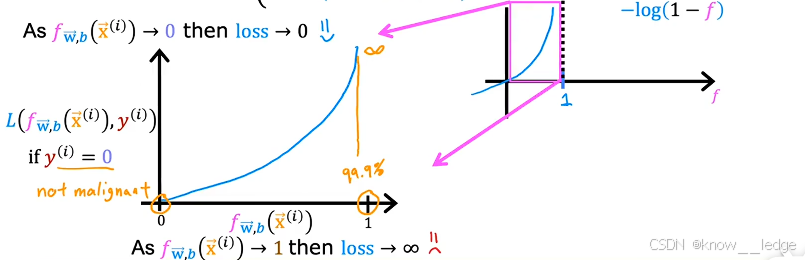
当 y ( i ) = 0 y^{(i)} = 0y(i)=0 时:
- 我们希望预测值越接近 0 越好;
- 若 f → 0 f \to 0f→0,则 − log ( 1 − f ) → 0 -\log(1 - f) \to 0−log(1−f)→0→ 损失小;
- 若 f → 1 f \to 1f→1,则 − log ( 1 − f ) → + ∞ -\log(1 - f) \to +\infty−log(1−f)→+∞→ 损失极大。
总结:预测值越接近真实标签,损失越小;越远,损失越大且增长极快。
2.3 统一写法(推荐)
我们能够将分段函数合并为一个简洁表达式:
L ( f w , b ( x ( i ) ) , y ( i ) ) = − y ( i ) log ( f w , b ( x ( i ) ) ) − ( 1 − y ( i ) ) log ( 1 − f w , b ( x ( i ) ) ) L(f_{w,b}(x^{(i)}), y^{(i)}) = -y^{(i)} \log(f_{w,b}(x^{(i)})) - (1 - y^{(i)}) \log(1 - f_{w,b}(x^{(i)}))L(fw,b(x(i)),y(i))=−y(i)log(fw,b(x(i)))−(1−y(i))log(1−fw,b(x(i)))
验证:
- 若 y ( i ) = 1 y^{(i)} = 1y(i)=1:第二项为 0,剩下− log ( f ) -\log(f)−log(f)
- 若 y ( i ) = 0 y^{(i)} = 0y(i)=0:第一项为 0,剩下− log ( 1 − f ) -\log(1 - f)−log(1−f)
完美匹配!
2.4 代价函数(整个训练集)
对所有 m mm个样本取平均,得到总代价函数:
J ( w ⃗ , b ) = 1 m ∑ i = 1 m L ( f w ⃗ , b ( x ⃗ ( i ) ) , y ( i ) ) J(\vec{w}, b) = \frac{1}{m} \sum_{i=1}^{m} L(f_{\vec{w},b}(\vec{x}^{(i)}), y^{(i)})J(w,b)=m1i=1∑mL(fw,b(x(i)),y(i))
代入损失函数表达式:
J ( w ⃗ , b ) = − 1 m ∑ i = 1 m [ y ( i ) log ( f w ⃗ , b ( x ⃗ ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − f w ⃗ , b ( x ⃗ ( i ) ) ) ] J(\vec{w}, b) = -\frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)} \log(f_{\vec{w},b}(\vec{x}^{(i)})) + (1 - y^{(i)}) \log(1 - f_{\vec{w},b}(\vec{x}^{(i)})) \right]J(w,b)=−m1i=1∑m[y(i)log(fw,b(x(i)))+(1−y(i))log(1−fw,b(x(i)))]
注意:这里没有1 2 \frac{1}{2}21!因为对数损失本身已具备良好的数学性质,无需额外系数简化求导。
物理意义上看,这种代价函数基于统计学中的最大似然估计原理,是最自然的选择之一
3. 实现梯度下降
梯度下降是训练逻辑回归模型的核心方法:通过不断调整参数w ww 和 b bb,让代价函数最小化。
3.1 为什么逻辑回归可以使用梯度下降?
- 逻辑回归的代价函数为:
J ( w ⃗ , b ) = − 1 m ∑ i = 1 m [ y ( i ) log ( f w ⃗ , b ( x ⃗ ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − f w ⃗ , b ( x ⃗ ( i ) ) ) ] J(\vec{w}, b) = -\frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)} \log(f_{\vec{w},b}(\vec{x}^{(i)})) + (1 - y^{(i)}) \log(1 - f_{\vec{w},b}(\vec{x}^{(i)})) \right]J(w,b)=−m1i=1∑m[y(i)log(fw,b(x(i)))+(1−y(i))log(1−fw,b(x(i)))]
其中:
- f w , b ( x ) = 1 1 + e − ( w x + b ) f_{w,b}(x) = \frac{1}{1 + e^{-(wx + b)}}fw,b(x)=1+e−(wx+b)1是Sigmoid函数;
- y ( i ) ∈ { 0 , 1 } y^{(i)} \in \{0, 1\}y(i)∈{0,1}是真实标签;
- m mm是训练样本数量。
这个代价函数是凸函数,只有一个全局最小值,因此可能使用梯度下降法稳定收敛到最优解
3.2 梯度下降更新规则
我们需要计算代价函数对参数的偏导数:
对权重 w j w_jwj 的梯度:
∂ J ∂ w j = 1 m ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) ) x j ( i ) \frac{\partial J}{\partial w_j} = \frac{1}{m} \sum_{i=1}^{m} \left( f_{w,b}(x^{(i)}) - y^{(i)} \right) x_j^{(i)}∂wj∂J=m1i=1∑m(fw,b(x(i))−y(i))xj(i)
对偏置 b bb 的梯度:
∂ J ∂ b = 1 m ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) ) \frac{\partial J}{\partial b} = \frac{1}{m} \sum_{i=1}^{m} \left( f_{w,b}(x^{(i)}) - y^{(i)} \right)∂b∂J=m1i=1∑m(fw,b(x(i))−y(i))
3.3 梯度下降公式(核心)
使用学习率 α \alphaα,每次迭代更新参数:
{ w j = w j − α ∂ J ∂ w j = w j − α m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) ⋅ x ⃗ j ( i ) b = b − α ∂ J ∂ b = b − α m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) j = 1 , 2 , … , n . \begin{cases} w_j = w_j - \alpha \dfrac{\partial J}{\partial w_j} = w_j - \dfrac{\alpha}{m} \displaystyle\sum_{i=1}^{m} \left( f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)} \right) \cdot \vec{x}_j^{(i)} \\ \\ b = b - \alpha \dfrac{\partial J}{\partial b} = b - \dfrac{\alpha}{m} \displaystyle\sum_{i=1}^{m} \left( f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)} \right) \end{cases} \quad \text j = 1,2,\dots,n.⎩⎨⎧wj=wj−α∂wj∂J=wj−mαi=1∑m(fw,b(x(i))−y(i))⋅xj(i)b=b−α∂b∂J=b−mαi=1∑m(fw,b(x(i))−y(i))j=1,2,…,n.
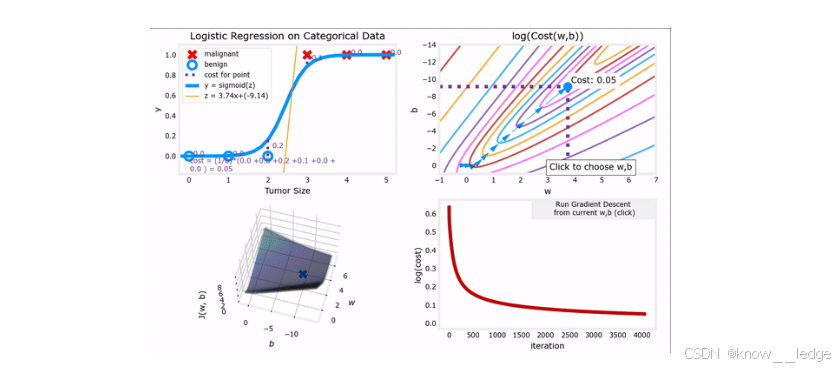
- 左图:Sigmoid 曲线拟合肿瘤数据,表明分类边界;
- 右图:在参数空间中,梯度下降沿着代价函数的“下坡”方向移动,逐步逼近最优解( w ∗ , b ∗ ) (w^*, b^*)(w∗,b∗)。
- 尽管模型不同,但梯度下降的数学形式与线性回归相同——这是计算上的巧合,也是其高效性的体现。
4. 过拟合与正则化
当模型在训练数据上表现很好,但在新数据上表现差时,说明它“学得太死”了——这就是过拟合。
过拟合和欠拟合,并学习如何用就是本节将带你理解什么正则化来克服这个障碍。
4.1 什么是过拟合和欠拟合?
大家通过一个简单的例子来理解三种模型状态:
假设我们要根据房屋面积预测房价,有以下三种情况:
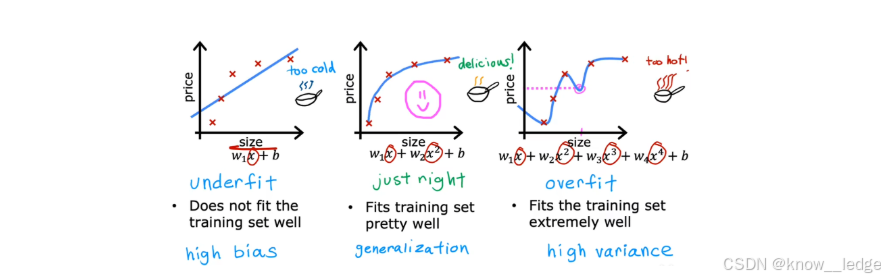
左图为欠拟合
- 模型太方便(比如只用一条水平线拟合);
- 无法捕捉数据的基本规律;
- 训练误差大,测试误差也大。
原因:模型复杂度太低,或特征太少。
中图为理想拟合
- 模型能抓住数据的整体趋势;
- 在训练集和新信息上都表现良好。
右图为过拟合
- 模型太繁琐(比如用高阶多项式穿过每一个点);
- 完美拟合训练材料,却把噪声也当成了规律;
- 训练误差很小,但测试误差很大。
原因:模型复杂度太高,或训练数据太少。
4.2 为什么过拟合是个障碍?
过拟合的模型就像一个“死记硬背的学生”:
- 考试前把练习题答案全背下来 → 训练准确率 100%;
- 但遇到新题就懵了 → 实际应用效果差。
在机器学习中,我们的目标是泛化能力(Generalization):
能对从未见过的数据做出准确预测。
过拟合会严重损害泛化能力!
4.3 解决过拟合的三种方式
- 扩大训练集:此时即使有很多特征,相比于训练集很小时,其拟合曲线也会相对平滑。
缺点是不一定能获取更多的训练数据。- 减少特征数:也称为“特征选择”。“特征选择”除了靠直觉,在Course2中也会介绍一种自动选择特征的方法。缺点是有可能会丢弃有用特征。
- 正则化:保留所有的特征,但对于某个很大的特征x j x_jxj,减小其参数w j w_jwj(通常不会调整参数b bb)
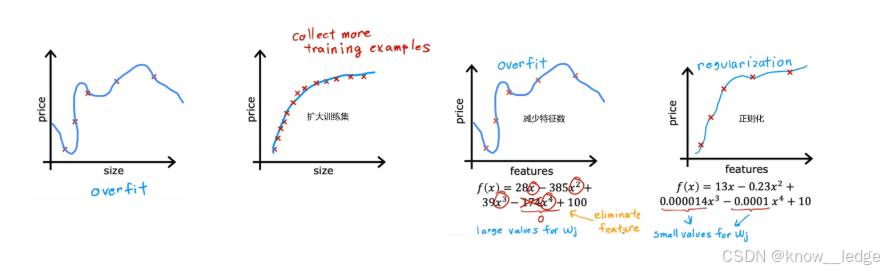
4.4 如何解决过拟合?—— 正则化
正则化:就是是一种防止过拟合的手艺,核心思想
在代价函数中加入一个“惩罚项”,限制模型参数不要变得太大。
为什么管用?
- 大的参数值往往意味着模型在“强行拟合噪声”;
- 限制参数大小,相当于让模型变得更“平滑”、“简单”。
正则化后的代价函数:
大家在原始代价函数后面加上一个正则项:
J ( w ⃗ , b ) = 1 m ∑ i = 1 m L ( f w ⃗ , b ( x ⃗ ( i ) ) , y ( i ) ) + λ 2 m ∑ j = 1 n w j 2 , λ > 0 J(\vec{w}, b) = \frac{1}{m} \sum_{i=1}^{m} L(f_{\vec{w},b}(\vec{x}^{(i)}), y^{(i)}) + \frac{\lambda}{2m} \sum_{j=1}^{n} w_j^2, \quad \lambda > 0J(w,b)=m1i=1∑mL(fw,b(x(i)),y(i))+2mλj=1∑nwj2,λ>0
注:正则化通常不包含偏置项b bb,因此 λ 2 m b 2 \frac{\lambda}{2m} b^22mλb2 一般省略。
其中:
- J ( w , b ) J(w, b)J(w,b)是原始的逻辑回归代价函数;
- λ \lambdaλ(lambda)是正则化参数,控制惩罚力度;
- m mm是样本数量;
- n nn是特征数量;
- 通常不对偏置项b bb 进行正则化。
正则化参数 λ \lambdaλ 的作用:
| λ \lambdaλ 值 | 效果 |
|---|---|
| 太小(如 0) | 几乎无正则化 → 可能过拟合 |
| 合适 | 平衡拟合与泛化 → 最佳性能 |
| 太大(如 10000) | 参数被过度压缩 → 可能欠拟合 |
通常依据交叉验证(Cross-Validation)来选择最佳λ \lambdaλ
4.5 正则化后的梯度更新公式
由于代价函数变了,梯度也要相应调整
对于每个权重w j w_jwj(j = 1 , 2 , . . . , n j = 1, 2, ..., nj=1,2,...,n):
∂ J ∂ w j = ∂ J ∂ w j + λ m w j \frac{\partial J_{\text{}}}{\partial w_j} = \frac{\partial J}{\partial w_j} + \frac{\lambda}{m} w_j∂wj∂J=∂wj∂J+mλwj
因此,梯度下降的更新规则变为:
w j = w j − α ∂ J ∂ w j = w j − α m ( ∑ i = 1 m [ ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) ⋅ x j ( i ) ] + λ w j ) w_j = w_j - \alpha \dfrac{\partial J}{\partial w_j} = w_j - \dfrac{\alpha}{m} \left( \displaystyle\sum_{i=1}^{m} \left[ (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}) \cdot x_j^{(i)} \right] + \lambda w_j \right)wj=wj−α∂wj∂J=wj−mα(i=1∑m[(fw,b(x(i))−y(i))⋅xj(i)]+λwj)
j = 1 , 2 , … , n j = 1,2,\dots,nj=1,2,…,n
而偏置项 b bb 不变:
b = b − α ∂ J ∂ b = b − α m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) b = b - \alpha \dfrac{\partial J}{\partial b} = b - \dfrac{\alpha}{m} \displaystyle\sum_{i=1}^{m} \left( f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)} \right)b=b−α∂b∂J=b−mαi=1∑m(fw,b(x(i))−y(i))
注意:这个额外的λ m w j \frac{\lambda}{m} w_jmλwj 项会让 w j w_jwj在每次更新时“自动缩小一点”,从而防止它变得过大。
下面来进一步分析参数的更新过程(同样也适用于“逻辑回归”中的正则方法):
w j = w j − α m ( ∑ i = 1 m [ ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) ⋅ x j ( i ) ] + λ w j ) = ( 1 − α λ m ) w j ⏟ 每次更新自动缩小 w j − α m ∑ i = 1 m [ ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) ⋅ x j ( i ) ] ⏟ 常规更新 \begin{aligned} w_j &= w_j - \frac{\alpha}{m} \left( \sum_{i=1}^{m} \left[ (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}) \cdot x_j^{(i)} \right] + \lambda w_j \right) \\ &= \underbrace{(1 - \alpha \frac{\lambda}{m}) w_j}_{\text{每次更新自动缩小} w_j} - \underbrace{\frac{\alpha}{m} \sum_{i=1}^{m} \left[ (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}) \cdot x_j^{(i)} \right]}_{\text{常规更新}} \end{aligned}wj=wj−mα(i=1∑m[(fw,b(x(i))−y(i))⋅xj(i)]+λwj)=每次更新自动缩小wj(1−αmλ)wj−常规更新mαi=1∑m[(fw,b(x(i))−y(i))⋅xj(i)]
- 第一项:添加正则化后,会在每次迭代过程中,都使参数w j w_jwj乘以一个略小于 1 的常数。
- 第二项:对于非正则化的线性回归,正常的梯度下降法更新过程。
小结:逻辑回归相关公式
逻辑回归模型:
f w ⃗ , b ( x ⃗ ) = g ( z ) = 1 1 + e − ( w ⃗ ⋅ x ⃗ + b ) f_{\vec{w},b}(\vec{x}) = g(z) = \frac{1}{1 + e^{-(\vec{w} \cdot \vec{x} + b)}}fw,b(x)=g(z)=1+e−(w⋅x+b)1代价函数:
J ( w ⃗ , b ) = − 1 m ∑ i = 1 m [ y ( i ) log ( f w ⃗ , b ( x ⃗ ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − f w ⃗ , b ( x ⃗ ( i ) ) ) ] + λ 2 m ∑ j = 1 n w j 2 , λ > 0 J(\vec{w}, b) = -\frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)} \log(f_{\vec{w},b}(\vec{x}^{(i)})) + (1 - y^{(i)}) \log(1 - f_{\vec{w},b}(\vec{x}^{(i)}))\right]+ \frac{\lambda}{2m} \sum_{j=1}^{n} w_j^2 , \quad \lambda > 0J(w,b)=−m1i=1∑m[y(i)log(fw,b(x(i)))+(1−y(i))log(1−fw,b(x(i)))]+2mλj=1∑nwj2,λ>0梯度下降:
{ w j = w j − α ∂ J ∂ w j = w j − α m ( ∑ i = 1 m [ ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) ⋅ x j ( i ) ] + λ w j ) b = b − α ∂ J ∂ b = b − α m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) j = 1 , 2 , … , n . \begin{cases} w_j = w_j - \alpha \dfrac{\partial J}{\partial w_j} = w_j - \dfrac{\alpha}{m} \left( \displaystyle\sum_{i=1}^{m} \left[ (f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)}) \cdot x_j^{(i)} \right] + \lambda w_j \right) \\ \\ b = b - \alpha \dfrac{\partial J}{\partial b} = b - \dfrac{\alpha}{m} \displaystyle\sum_{i=1}^{m} \left( f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)} \right) \end{cases} \quad \text j = 1,2,\dots,n.⎩⎨⎧wj=wj−α∂wj∂J=wj−mα(i=1∑m[(fw,b(x(i))−y(i))⋅xj(i)]+λwj)b=b−α∂b∂J=b−mαi=1∑m(fw,b(x(i))−y(i))j=1,2,…,n.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号