完整教程：Eigen：一个好用的线性代数运算的C++算法库

目录

1.简介

2.安装与配置

3.windows下CMake用VS2022编译

3.1.下载 Eigen 源码

3.2.配置与编译

3.3.遇到的问题

4.核心基础

5.运算与代数

6.高级功能

7.适用场景

8.性能与注意事项

9.总结

1.简介

        Eigen 是一个开源的 C++ 模板库，专注于线性代数运算，广泛用于处理矩阵、向量、数值求解等问题。它以高效性、易用性和丰富的功能著称，被广泛应用于机器人学、计算机图形学、机器学习、科学计算等领域。

        它的核心功能：

1.模板库设计：无需编译链接，只需包含头文件即可使用（纯头文件库），易于集成到项目中。

2.高效性：通过模板元编程优化，运算速度接近手写优化代码（甚至在某些场景下超越传统 BLAS/LAPACK 库）。

3.跨平台：支持 Windows、Linux、macOS 等主流系统，兼容各种编译器（GCC、Clang、MSVC 等）。

4.模块化设计：只需包含所需的模块，编译快速。

5.丰富的API:

  • 基础：矩阵 / 向量的创建、加减乘除、转置、逆、行列式等。
  • 进阶：线性方程组求解（Ax=b）、矩阵分解（LU、QR、SVD、Cholesky 等）、特征值 / 特征向量计算。
  • 扩展：支持稀疏矩阵（适合大型稀疏问题）、复数运算、固定大小 / 动态大小矩阵等。

2.安装与配置

方法一（推荐）：使用包管理器

  • Linux (apt): sudo apt install libeigen3-dev

  • MacOS (Homebrew): brew install eigen

  • Windows (vcpkg): vcpkg install eigen3

方法二：手动安装从 Eigen 官网 下载最新版本，解压后将 Eigen 目录放到你的项目的包含路径中。

https://eigen.tuxfamily.org/

在项目中使用：在你的 C++ 源文件中，只需包含所需的头文件即可。

#include 
#include  // 核心模块，包含Matrix和Array类
#include  // 稠密矩阵代数运算（逆、特征值等）
int main() {
    // 你的代码
    return 0;
}

编译命令示例 (需指定头文件路径)：

g++ -I /path/to/eigen/ your_program.cpp -o your_program

如果你的系统包管理器安装的 Eigen，路径通常是 /usr/include/eigen3 或 /usr/local/include/eigen3。

3.windows下CMake用VS2022编译

3.1.下载 Eigen 源码

从 Eigen 官网 下载最新版本（如 3.4.0），或通过 Git 克隆：

git clone https://gitlab.com/libeigen/eigen.git

解压后得到源码目录（假设为 D:\eigen-src）。

3.2.配置与编译

1) 用CMake-gui配置

创建构建目录

在源码目录外新建一个构建目录（如 D:\eigen-build），用于存放 CMake 生成的项目文件和编译产物。

运行 CMake 配置

  • 打开 “CMake GUI”（或通过命令行），在 “Where is the source code” 中填入 Eigen 源码目录（D:\eigen-src）。
  • 在 “Where to build the binaries” 中填入构建目录（D:\eigen-build）。
  • 点击 “Configure”，在弹出的窗口中选择编译器：
    • “Specify the generator for this project” → 选择 “Visual Studio 17 2022”。
    • “Optional platform for generator” → 根据需求选择 “x64” 或 “x86”（推荐 x64）。
    • 点击 “Finish”，CMake 会自动检测环境并加载配置选项。

配置编译选项（可选）

CMake 配置界面会显示 Eigen 的可选编译选项，常用选项如下：

  • BUILD_TESTING：是否编译测试程序（默认 ON，如需仅用 Eigen 库可设为 OFF）。
  • EIGEN_BUILD_DOC：是否生成文档（需 Doxygen，默认 OFF）。
  • EIGEN_USE_BLAS/EIGEN_USE_LAPACK：是否使用外部 BLAS/LAPACK 库（如需加速线性代数运算，可开启并指定库路径）。
  • EIGEN_BUILD_PKGCONFIG：生成 pkg-config 配置文件（Linux 常用，Windows 可选 OFF）。

根据需求修改后，再次点击 “Configure” 确保选项生效，然后点击 “Generate” 生成 VS2022 项目文件（.sln）。

2) 用 VS2022 编译

进入构建目录（D:\eigen-build），双击 Eigen.sln 用 VS2022 打开项目。在 VS2022 工具栏中，选择编译模式（Debug 或 Release）和平台（需与 CMake 配置一致，如 x64）。

3) 直接用CMake的命令行编译

cd  D:\eigen-build

mkdir build

cd build

cmake ..

cmake --build . --config Debug

编译完毕会在相应的目录生成目标文件，如下图所示：

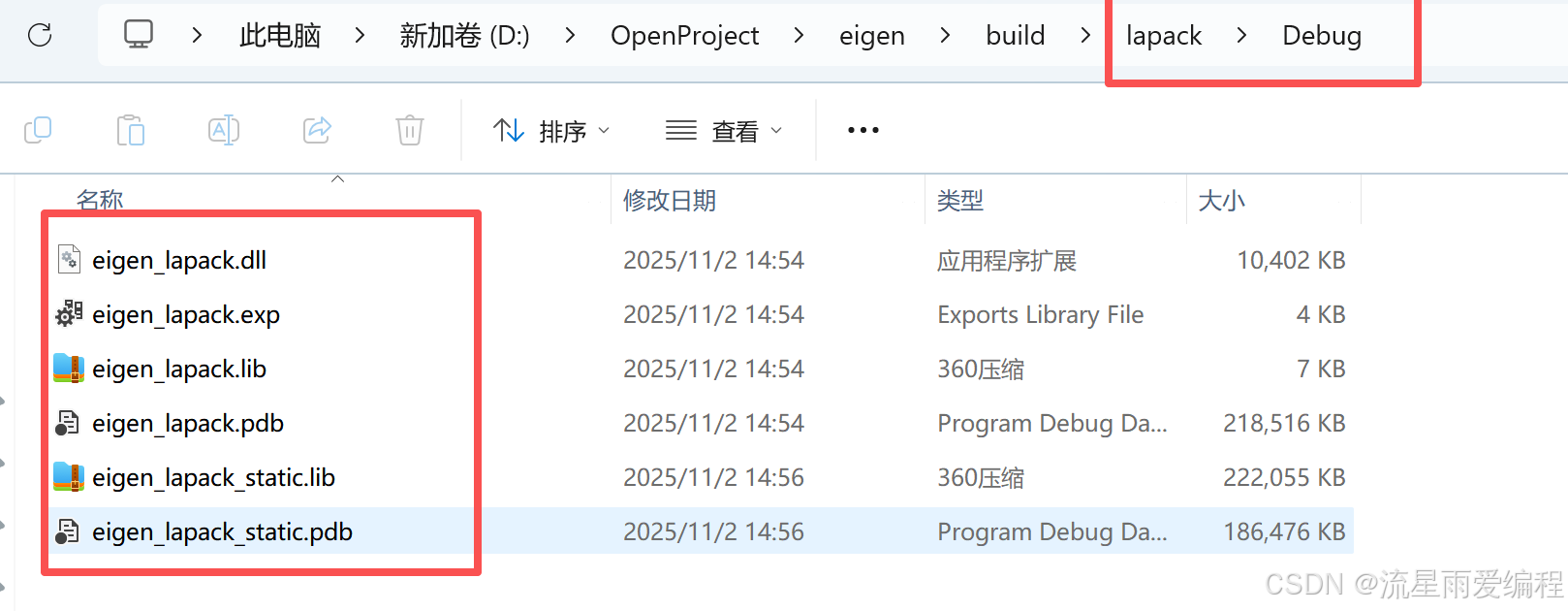
3.3.遇到的问题

出现报错：D:\OpenProject\eigen\lapack\complex_double.cpp(1,1): error C1128: 节数超过对象文件格式限制: 请使用 /bigobj 进行编译 [D:\OpenProject\eigen\ build\lapack\eigen_lapack_static.vcxproj]

这个错误是由于 Visual Studio 编译器默认生成的目标文件（.obj）支持的 “节（section）数量” 有限（默认最多 65536 个），而 Eigen 的 LAPACK 模块代码复杂（包含大量模板实例化），导致生成的节数超过了这个限制。解决方法是通过编译器选项 /bigobj 增加目标文件的节数上限。

具体解决步骤：

方法 1：直接在 Visual Studio 项目中配置（适用于手动管理项目）

  1. 在解决方案资源管理器中，找到报错的项目（这里是 eigen_lapack_static），右键点击它，选择 “属性”（快捷键：Alt+Enter）。
  2. 在属性页左侧导航栏，依次展开 “配置属性”→“C/C++”→“命令行”。
  3. 在右侧的 “附加选项” 输入框中，添加编译选项：/bigobj。
  4. 点击 “应用”→“确定”，重新编译项目即可。

方法 2：如果使用 CMake 构建项目（推荐，更易维护）

如果你的 Eigen 项目是通过 CMake 生成的 Visual Studio 解决方案，需要在 CMakeLists.txt 中添加 /bigobj 选项，确保编译时自动生效：

在 CMakeLists.txt 中加入以下代码（放在项目配置前）：

# 为 C++ 编译器添加 /bigobj 选项（仅针对 MSVC 编译器）
if(MSVC)
    set(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} /bigobj")
endif()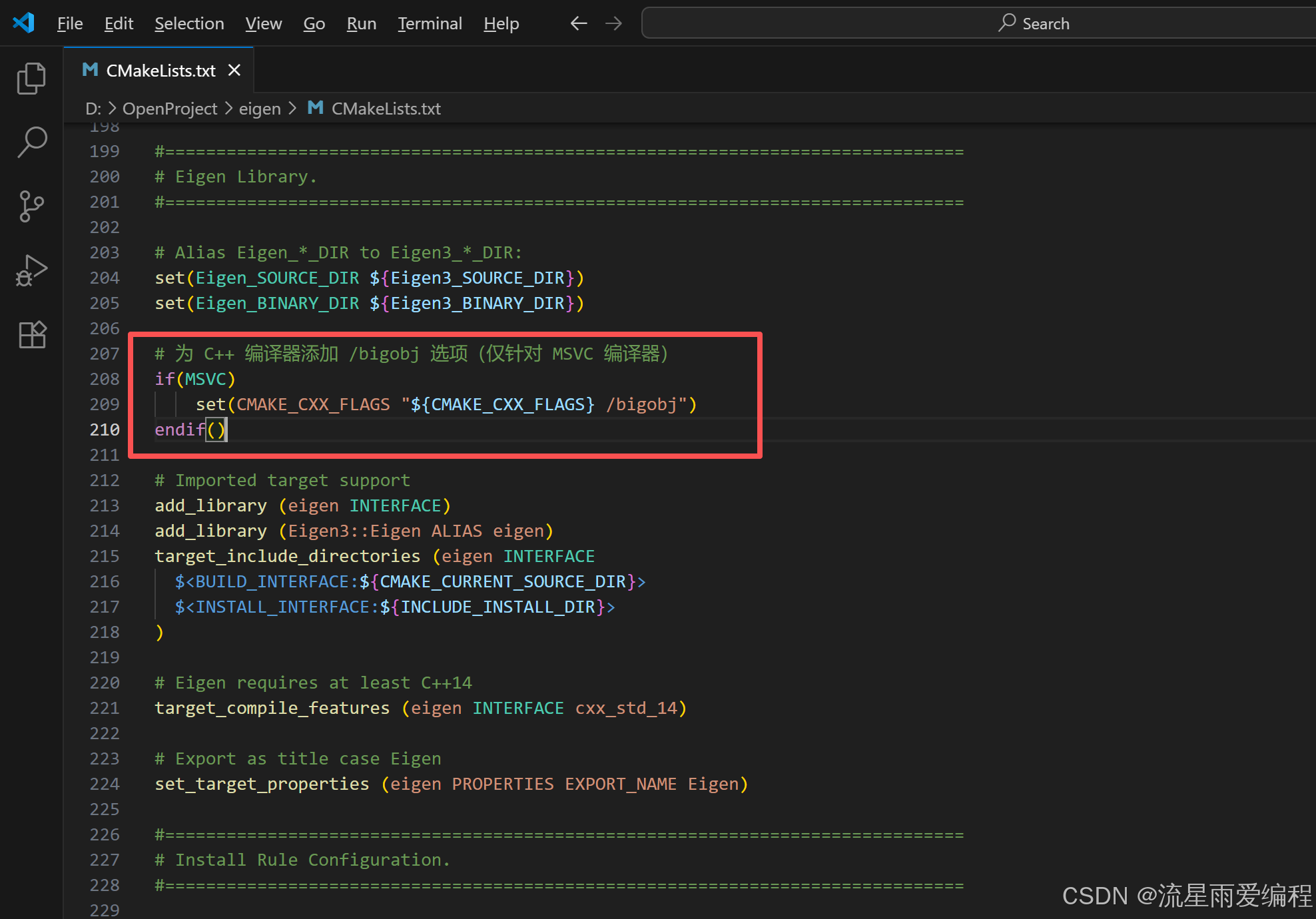

然后重新生成 Visual Studio 项目并编译或直接CMake命令行编译，即可解决问题。

原理说明

/bigobj 是 Visual Studio（MSVC）编译器的专用选项，它将目标文件支持的最大节数从默认的 65536 提升到 4,294,967,295（2^32-1），足以应对复杂代码（如大量模板实例化的 Eigen LAPACK 模块）生成的节数需求。

该选项仅影响编译阶段的目标文件生成，对最终程序的运行逻辑和性能无任何影响，可放心使用。

4.核心基础

1.矩阵与向量的创建

Eigen 中矩阵的定义格式为 Matrix<Scalar, Rows, Cols>，其中：

  • Scalar：数据类型（如 float、double、int）。
  • Rows/Cols：行数 / 列数（Dynamic 表示动态大小，编译时不确定）。

常用别名（简化定义）：

  • MatrixXd：动态大小的 double 矩阵（Matrix<double, Dynamic, Dynamic>）。
  • Vector3f：3 维 float 向量（Matrix<float, 3, 1>）。
  • Matrix2d：2x2 的 double 矩阵（Matrix<double, 2, 2>）。
// 固定大小矩阵（编译时确定维度，栈分配，速度更快）
Eigen::Matrix2d m2;  // 2x2 double 矩阵
m2 << 1, 2,          // 初始化：按行填充
      3, 4;
// 动态大小矩阵（运行时确定维度，堆分配，适合大型矩阵）
Eigen::MatrixXd m(3, 3);  // 3x3 double 矩阵（动态大小）
m = Eigen::MatrixXd::Random(3, 3);  // 随机初始化
// 向量（可视为列矩阵）
Eigen::Vector3f v3(1.0f, 2.0f, 3.0f);  // 3 维 float 向量
Eigen::VectorXd v(4);  // 4 维动态 double 向量
v << 1, 2, 3, 4;       // 初始化

2.元素访问与操作

Eigen::MatrixXd m(2, 2);
m(0, 0) = 3; // 通过 (i, j) 访问元素，下标从 0 开始
m(1, 0) = 2.5;
m(0, 1) = -1;
m(1, 1) = m(1, 0) + m(0, 1);
std::cout << m << std::endl;
// 输出：
//  3  -1
// 2.5 1.5
Eigen::Vector3d v(1, 2, 3);
std::cout << v[0] << ", " << v(1) << std::endl; // 向量可以用 [] 或 () 访问
// 获取矩阵信息
int rows = m.rows();
int cols = m.cols();
int size = v.size(); // 对于向量

5.运算与代数

Eigen 重载了 C++ 算术运算符，使矩阵运算语法非常直观。

1.基本算术运算

假设 a, b 是相同类型的矩阵，s 是一个标量。

// 加减法
Eigen::Matrix2d c = a + b;
Eigen::Matrix2d d = a - b;
// 标量乘除法
a * s;
a / s;
s * a;
// 矩阵乘法（最重要！）
Eigen::MatrixXd e = a * b; // 注意维度必须匹配
// a(2x3) * b(3x4) = e(2x4)
// 转置 (transpose()) 和共轭转置 (adjoint())
Eigen::Matrix2d f = a.transpose();
// 注意：对于实数矩阵，adjoint() 等价于 transpose()
// 点乘和叉乘（仅对向量）
Eigen::Vector3d v, w;
double dot = v.dot(w);    // 点积
Eigen::Vector3d cross = v.cross(w); // 叉积 (必须是3维向量)

2.逐元素运算（Array）

有时你需要对矩阵的每个元素单独操作（例如，A * B 是矩阵乘法，而不是逐元素乘法）。这时可以使用 Array 类或将 Matrix 转换为 Array。

// 方法一：直接使用 Array 类（声明和初始化与 Matrix 类似）
Eigen::ArrayXf a = Eigen::ArrayXf::Random(5);
Eigen::ArrayXf b = Eigen::ArrayXf::Random(5);
Eigen::ArrayXf c = a * b; // 逐元素乘法
Eigen::ArrayXf d = a / b; // 逐元素除法
Eigen::ArrayXf e = a.abs(); // 取绝对值
Eigen::ArrayXf f = a.sqrt(); // 平方根
Eigen::ArrayXf g = a.pow(2); // 平方
// 方法二：Matrix 和 Array 相互转换
Eigen::MatrixXf mat(2, 2);
Eigen::MatrixXf mat2(2, 2);
// ...
Eigen::ArrayXf arr = mat.array();       // Matrix -> Array
Eigen::MatrixXf mat3 = arr.matrix();    // Array -> Matrix
// 对 Matrix 进行逐元素操作
Eigen::MatrixXf result = mat.array() * mat2.array(); // 逐元素乘
mat.transpose();//转置矩阵
mat.inverse();//逆矩阵
mat.conjugate();//共轭矩阵
mat.adjoint();//伴随矩阵
mat.trace();//矩阵的稚
mat.eigenvalues();//矩阵的特征值
mat.determinant();//矩阵求行列式的值
mat.diagonal();//矩阵对角线元素
mat.sum();//矩阵所有元素求和
mat.prod();//矩阵所有元素求积
mat.mean();//矩阵所有元素求平均
mat.maxCoeff();//矩阵最大值
mat.minCoeff();//矩阵的最小值
Matrix::Identity();//单位矩阵
dot();//点积
cross();//叉积

3.块操作 (Block Operations)

用于获取或操作矩阵的子块。

Eigen::MatrixXd m(4, 4);
// 获取块： .block(startRow, startCol)
Eigen::Matrix2d topLeft = m.block<2, 2>(0, 0); // 固定大小块
Eigen::MatrixXd bottomRight = m.block(2, 2, 2, 2); // 动态大小块
// 获取行/列
Eigen::VectorXd row = m.row(1);
Eigen::VectorXd col = m.col(2);
// 获取对角向量
Eigen::VectorXd diag = m.diagonal();
// 块操作也可用作左值
m.block(0, 0, 2, 2) = Eigen::Matrix2d::Identity(); // 将左上角2x2块设为单位阵

4.矩阵约简 (Reductions)

Eigen::MatrixXf mat = Eigen::MatrixXf::Random(3, 3);
std::cout << "Sum: " << mat.sum() << std::endl;       // 所有元素和
std::cout << "Prod: " << mat.prod() << std::endl;     // 所有元素积
std::cout << "Mean: " << mat.mean() << std::endl;     // 所有元素均值
std::cout << "Min: " << mat.minCoeff() << std::endl;  // 最小系数
std::cout << "Max: " << mat.maxCoeff() << std::endl;  // 最大系数
std::cout << "Trace: " << mat.trace() << std::endl;   // 迹（对角线和）
// 获取极值的位置
Eigen::MatrixXf::Index minRow, minCol, maxRow, maxCol;
float minVal = mat.minCoeff(&minRow, &minCol);
float maxVal = mat.maxCoeff(&maxRow, &maxCol);

5.解线性方程组 (Ax = b)

Eigen 提供了多种直接法和迭代法求解器。

x = A.ldlt().solve(b));  // A sym. p.s.d.    #include 
x = A.llt() .solve(b));  // A sym. p.d.      #include 
x = A.lu()  .solve(b));  // Stable and fast. #include 
x = A.qr()  .solve(b));  // No pivoting.     #include 
x = A.svd() .solve(b));  // Stable, slowest. #include

例子：

// 以 LU 分解为例（最常用）
Eigen::Matrix3f A;
Eigen::Vector3f b;
A << 1, 2, 3,
     4, 5, 6,
     7, 8, 10;
b << 3, 3, 4;
// 直接求解：A.lu().solve(b)，但更推荐创建分解对象
Eigen::Vector3f x = A.partialPivLu().solve(b); // 使用部分主元LU分解
// 或者
// Eigen::Vector3f x = A.colPivHouseholderQr().solve(b); // QR分解，更稳定
// Eigen::Vector3f x = A.llt().solve(b); //  Cholesky分解，要求A正定
std::cout << "The solution is:\n" << x << std::endl;
// 检查误差
std::cout << "Error: " << (A * x - b).norm() << std::endl;

6. 特征值与特征向量

// 适用于自伴矩阵（对称/厄米特矩阵）使用 SelfAdjointEigenSolver
// 适用于一般方阵使用 EigenSolver 或 ComplexEigenSolver
Eigen::Matrix2f A;
A << 1, 2, 2, 3;
Eigen::SelfAdjointEigenSolver eigensolver(A);
if (eigensolver.info() != Eigen::Success) {
    std::cout << "Eigen decomposition failed!" << std::endl;
    return;
}
std::cout << "The eigenvalues of A are:\n" << eigensolver.eigenvalues() << std::endl;
std::cout << "The eigenvectors of A are:\n" << eigensolver.eigenvectors() << std::endl;

7.几何模块 (Geometry Module)

Eigen 的 Geometry 模块提供了各种几何变换。

#include 
// 2D/3D 变换类型
Eigen::Vector2f p(1.0, 2.0);
Eigen::Vector3f p3(1.0, 2.0, 3.0);
// 旋转
Eigen::Rotation2Df rot2(M_PI / 4); // 2D 旋转 45 度
Eigen::AngleAxisf rot3(M_PI / 2, Eigen::Vector3f::UnitZ()); // 绕 Z 轴旋转 90 度
Eigen::Quaternionf q = Eigen::Quaternionf::Identity(); // 四元数
// 变换（仿射/射影）
Eigen::Isometry3f T = Eigen::Isometry3f::Identity(); // 4x4 齐次变换矩阵
T.translate(Eigen::Vector3f(1, 2, 3));
T.rotate(q);
// 应用变换
Eigen::Vector2f p_rotated = rot2 * p;
Eigen::Vector3f p3_transformed = T * p3; // 变换点
std::cout << "Transformed point: " << p3_transformed.transpose() << std::endl;

6.高级功能

  • 稀疏矩阵：通过 Eigen::SparseMatrix<Scalar> 处理大型稀疏矩阵（非零元素少），节省内存和计算量，支持稀疏线性方程组求解（如共轭梯度法）。
  • 矩阵分解：提供 LU（稠密矩阵快速分解）、QR（数值稳定分解）、SVD（奇异值分解）等，用于数据降维、最小二乘问题等。
  • 几何模块：支持旋转矩阵、四元数、欧拉角等，适合机器人姿态计算、图形学变换等场景（需包含 Eigen/Geometry）。

7.适用场景

  • 科学计算：数值模拟、数据分析、微分方程求解等；
  • 工程领域：机器人学（运动学 / 动力学计算）、控制理论（状态方程求解）；
  • 计算机图形学：3D 变换、相机标定、光照计算；
  • 机器学习：矩阵运算密集型任务（如神经网络权重更新、特征降维）。

8.性能与注意事项

1.启用编译器优化：使用 -O2 或 -O3 标志编译，Eigen 的性能会得到极大提升。

2.尽量使用固定大小矩阵：对于小尺寸矩阵（通常 16x16 以下），固定大小矩阵允许编译器进行更好的优化。

3.避免滥用 auto 关键字：由于表达式模板，auto 可能会得到中间表达式类型而非最终计算结果。在赋值时，明确声明目标矩阵类型。

// 不好的做法：
auto result = A * B + C; // 'result' 可能是一个复杂的表达式模板类型
// 好的做法：
Eigen::MatrixXd result = A * B + C; // 表达式被强制求值并存入 MatrixXd

4.注意混叠 (Aliasing)：A = A * B 是安全的，Eigen 会做临时变量优化。但 A = A.transpose() 是不安全的，因为赋值前原矩阵已被修改。不安全操作应使用 .eval() 或 A.transposeInPlace()。

// 错误！
A = A.transpose(); // 未定义行为！
// 正确方法 1
A = A.transpose().eval();
// 正确方法 2 (更高效)
A.transposeInPlace();

9.总结

        Eigen 以 “高效、易用、灵活” 为核心优势，是 C++ 领域处理线性代数问题的首选库之一。无论是基础矩阵运算还是复杂数值求解，其丰富的功能和跨平台特性都能满足从学术研究到工业开发的多样化需求。如需深入学习，可参考 官方文档 获取更详细的 API 说明和示例。

posted @ 2026-01-28 20:52  clnchanpin  阅读(15)  评论(0)    收藏  举报