专题二 -- 滑动窗口 - 指南

一.滑动窗口概述

滑动窗口算法是一种高效的算法思想，常用于处理字符串或数组中的子串、子数组挑战，例如最长子串、最小覆盖子串等。它通过维护一个动态窗口，利用双指针（左指针和右指针）来调整窗口大小，从而优化暴力枚举的时间复杂度。

基本思想

滑动窗口的核心在于动态调整窗口的范围。右指针不断扩展窗口以满足条件，左指针则在条件不满足时缩小窗口。通过这种方式，可以避免重复计算，降低时间复杂度。

以下是滑动窗口的通用框架：

left, right = 0, 0 # 初始化左右指针

while right < len(s): # 右指针遍历整个字符串

window.add(s[right]) # 将右指针指向的元素加入窗口

right += 1 # 扩大窗口

while window不满足条件: # 当窗口不满足条件时

window.remove(s[left]) # 移除左指针指向的元素

left += 1 # 缩小窗口

# 在这里更新结果，例如记录最大值或最小值

二.OJ测试题

还是老套路，我会讲解一些OJ题目带大家来了解滑动窗口是怎么控制窗口最终得出答案的。

1.长度最小的子数组

题目描述：

给定一个含有 n个正整数的数组和一个正整数 target 。

找出该数组中满足其总和等于target的长度最小的子数组[numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

暴力解法：第一次for循环定起点，第二层循环一直从起点位置相加后面的数直到当前和大于target，接着比较此时的长度是否为最小值，再选择下一个节点进入循环继续重复相加的操作。

这里使用 target = 6, nums = [2,3,1,2,4,3] 来做示例讲解：

当我们从2开始相加的时候，第一次相加2 + 3 = 5，小于目标值，所以继续第二次相加 5 + 1 = 6 此时等于目标值，记录这个长度，开始枚举3。

从三开始相加的时候，第一次相加3 + 1 = 4，小于目标值，所以继续相加 4 + 2 = 6 此时等于目标值，记录该长度，开始继续枚举下一个数。

细心的同学应该会发现了，这两次相加有一个重叠的部分，当第二次相加的时候再重头开始相加好像有点多次一举了，大家可以用第一次得到的和减去前一个起点，而不用从头开始继续相加，减去一个数的该操作叫做出窗口。继而继续加下一个值，这一步叫做进窗口。框中的那个部分就是窗口，在近窗口以后需对其中的数据和进行判断，如果大于目标值就需出窗口，基于我们需要将窗口等于目标值。实际上在滑动的时候应该是2 + 3 + 1 + 2 = 8，此时大于6，需要一直减去左边的值出窗口，直到窗口内的数据和不再大于目标值。结束出窗口以后需要判断此时窗口内的值是否等于目标值，如果相等就记录长度。此时2出了以后，其中的数据还有3 + 1 + 2 = 6，等于目标值，记录长度。有的同学会问了，那么开始的2 3 1不就错过了，完整的步骤应该是：定义一个left和right，由left来指向出窗口的信息，right指向进窗口的内容，直到right < size的时候循环结束。那么在2 + 3 + 1的时候此时刚好等于目标值，不需要出窗口执行，接着就进入判断结果，符合目标值长度记录，再下一次进窗口以后就需要像上面说的情况出窗口了。

具体的代码以及测试：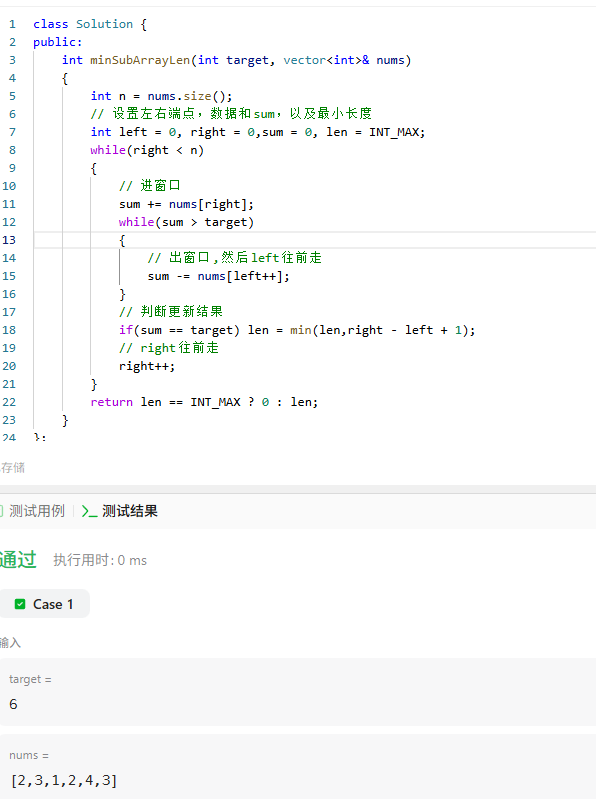

2.⽆重复字符的最⻓⼦串

题目描述：

给定一个字符串 s ，请你找出其中不含有重复字符的 最长 子串的长度。

这道题目求的是区间长度，也行使用滑动窗口来克服。暴力解法类似上面求一个数组中一段区间内的和，两个for枚举一段区间的子串，然后判断区间内是否由相同字符即可。

聪明的同学肯定发现了这个题目和上面的有异曲同工之妙，当a为起点枚举到abca后此时的最长不重复子串是abc，所以到b为起点进行枚举,bcab，然而这之间重叠了a为起点而枚举的一部分，所以当枚举b的时候我们可以在a以及枚举的区间把第一个a移出去，那么此时bca这个区间内就没有相同的值了，也就是出窗口操作。接着这个区间继续遍历下一个字符，也就是进窗口的操作。只有当区间内的字符出现了重复才会出窗口，那么此时出窗口和进窗口的逻辑关系我们都理清了，我们只需要在出了窗口以后跟新结果即可，因为此时必然不会出现重复字符。

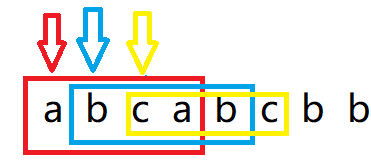
大于1那么就一直出窗口直到等于1。就是那么如何判断此时窗口内的字符是否有重复的呢？难道每次都要用个string对象加上当前进窗口的字符，之后使用strcmp来比较吗？在比较是否会出现重复数字或者字符这一类问题的时候，大家许可利用哈希表来储存之前出现过的信息，源于只有在新插入的那个瞬间才会出现重复数据，我们可能在插入这个字符以后判断一下这个字符是否只有一个，要

当窗口的内容为ghbcasb的时候，出现了重复字符，所以需要出窗口，一直把ghb出了窗口此时才没有重复字符，出窗口的循环才会结束。在此之前蓝色框内的素材早就在上一次大循环记录了这一次的长度，不必担心因为出窗口而忽略这个计算。

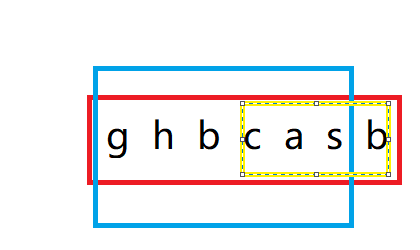
具体代码以及实现：

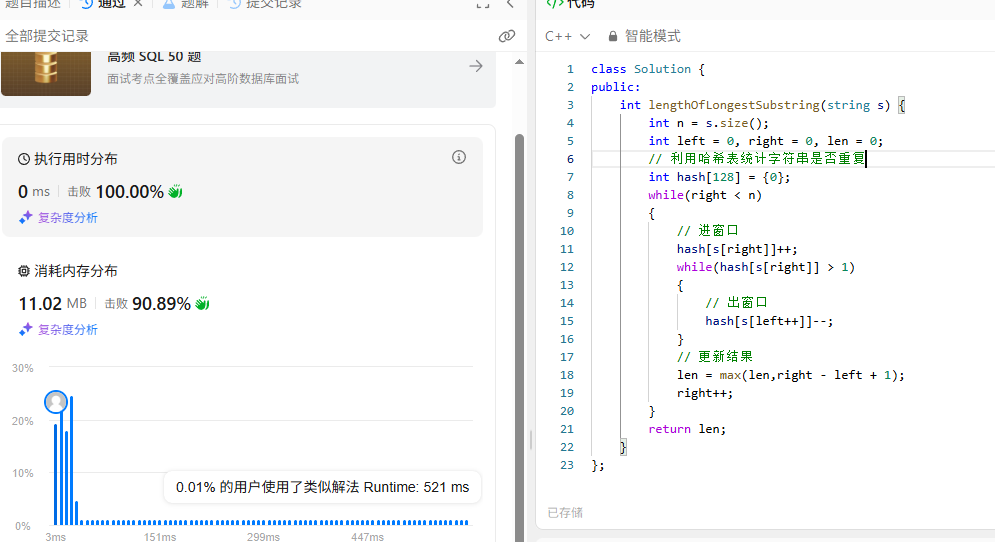
3.最⼤连续 1 的个数 III

题目描述：

给定一个二进制数组 nums 和一个整数 k，假设最多可以翻转 k 个 0 ，则返回执行操作后 数组中连续 1 的最大个数 。

示例 1：

输入：nums = [1,1,1,0,0,0,1,1,1,1,0], K = 2输出：6 解释：[1,1,1,0,0,1,1,1,1,1,1]

从 0 翻转到 1，最长的子数组长度为 6。

暴力解法：两层循环。枚举从第i个位置一直找连续的1，然后出现k个0以后统计当前长度。

合法的子区间，然后再统计一下合法区间的长度即可。就是优化：题意是求一段连续的区间，并且前面枚举的时候还是会有重叠的区域，那么还是许可利用滑动窗口，但是此时控制这个子数组也就是窗口的大小的其实就是K的值。大家可以在素材进窗口以后统计一下当前0的数量，如果大于K值，那么此时就要出窗口，直到窗口内的0等于K值，因为此时才

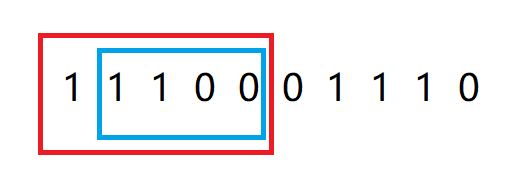
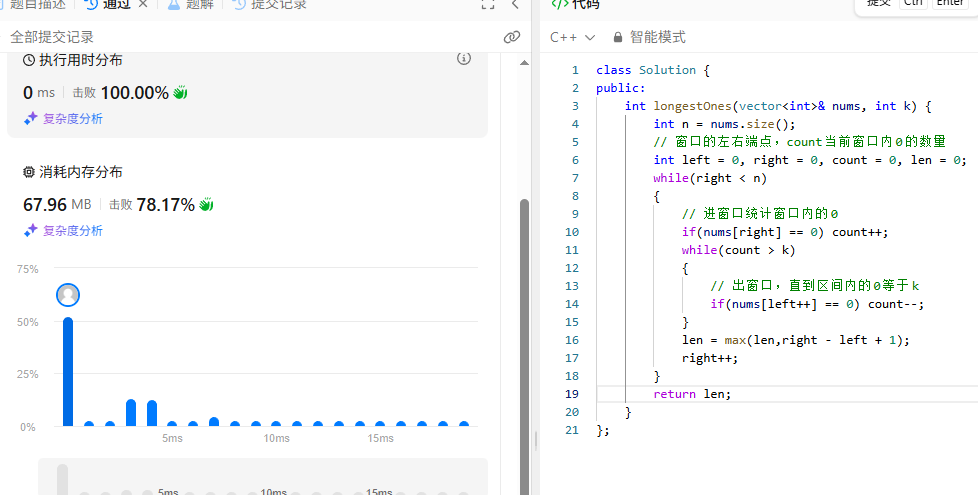
具体代码以及实现：

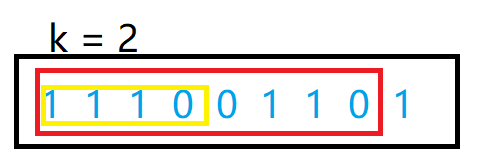
通过这里用count统计了窗口0的数量，所以无论0在哪个位置，只要count>k那么这个区间就不合法，我们需一直从左边开始出窗口直到合法。在下面这个示例中，当窗口为11100110的时候窗口不合法，左边一直出窗口，将1110全部出去以后，剩下的0110窗口才合法。其中的0011这个窗口会被忽略，但是它是具备在1110011区间的，我们要找到地是最长区间，所以能够直接忽略，也没必要去枚举这个区间，它必然不会是最终答案区间。

4.将 x 减到 0 的最⼩操作数

题目描述：

给你一个整数数组 nums 和一个整数 x 。每一次操作时，你应当移除数组 nums 最左边或最右边的元素，然后从 x 中减去该元素的值。请注意，需要 修改数组以供接下来的处理使用。

如果可以将 x恰好 减到 0 ，返回 最小操作数 ；否则，返回 -1 。

解题思路：

这道题目看起来与滑动窗口没有什么关系，但是通过下面这个例子我们会发现，我们并不需要直接去求出两边到底减多少次，由于这是随机的，我们无法控制。但是我们会发现除了红色框被减去的，中间蓝色框的那部分是连续的。整个数组的和sum = red + blue，而red部分等于x，那么blue部分的值也能够确定了，所以我们就可以通过滑动窗口来求一段连续的子数组，只要这个数组的和等于sum - x即可，这个就是合法窗口的条件。当窗口中的数据大于sum - x那么左边出窗口，当窗口材料和小于sum - x，进窗口。

还需要注意的是，我们需要求的是减去x的最小操作数，也就意味着中间那段子数组越长，两边的操作数越小，所以结果更新条件也有了，在末了返回结果的时候需要用n-1中间那段子数组的长度才能得到最终的操作数。

具体代码以及测试：

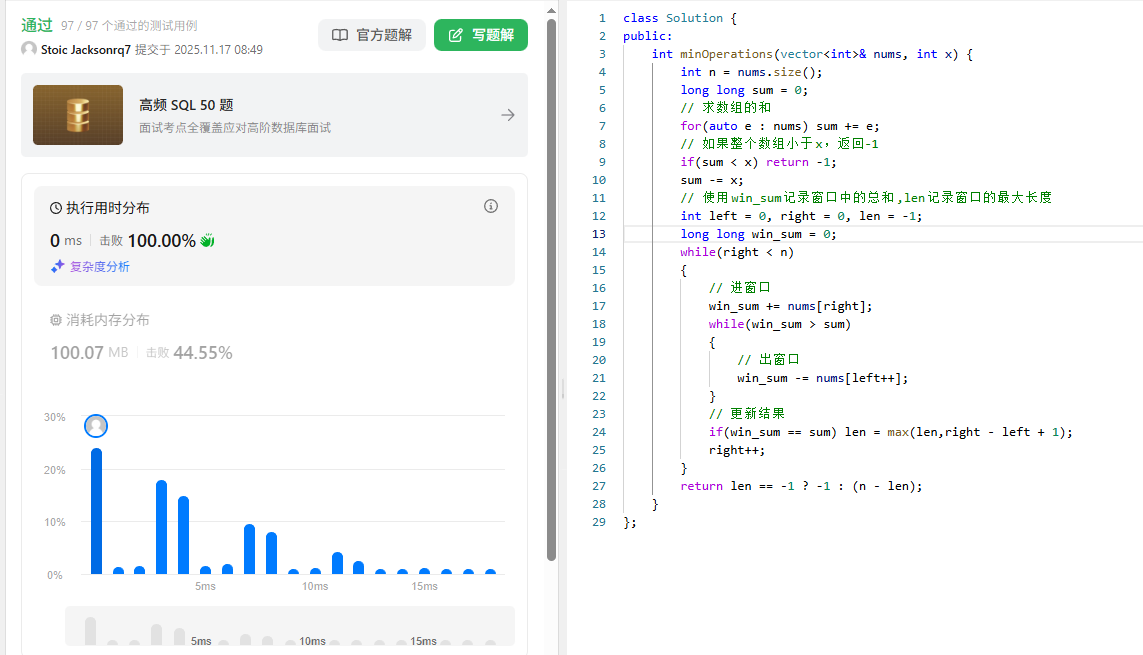
5.⽔果成篮

题目描述：

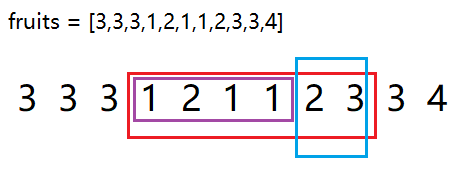
该题目的意思是给定一个fruits数组，在其中找出一段区间内只有两个不同元素的最长子区间。

暴力解法：两个for循环不断从每一个下标开始枚举，记录当前数组中不同元素的个数，超过两个就进行下一个循环。

对于这种求一段子区间数组的问题相信同学们都发现了，大多数都可以使用滑动窗口，缘于滑动窗口必须是连续的，只是每次出窗口的判断条件不同，也就是合法条件不相同。这道题目的合法窗口的条件就是窗口内的元素只有两种。要达到这个条件，就要知道窗口中的元素种类和各个种类的元素个数，我们需要确保当插入新元素以后，将其中一个元素完全移除窗口。那么如何确保窗口内的元素只有两种，用两个变量来维护吗？用什么类型的变量既可以表示当前元素种类，又可能记录它的数量，没错就是unodered_map。

最大子区间，所以能够直接忽略而不用担心出了窗口记录不到。就是在下面该示例中，当我们遍历到窗口12112再进一个数据3以后就需要出窗口，从左边一直出1211，直到窗口中的元素还剩23，开始新的一轮进窗口。其中可能会忽略一些组合比如211,11，然而这两个组合都是包括在12112这个窗口中的，因为我们求的

具体代码以及测试：

具体代码中我并没有启用unodered_map来储存当前窗口中元素的总类和个数，而是使用了一个数组来模拟，以及利用count记录当前元素总类。当然你也可以启用unodered_map，然后用map.size()来求当前元素的个数，只是map.count()在查找某一个元素的时候会产生额外的时间复杂度，不过map查找的时间复杂度是o(logn)，与本题o(n)不是一个量级，也允许忽略不计。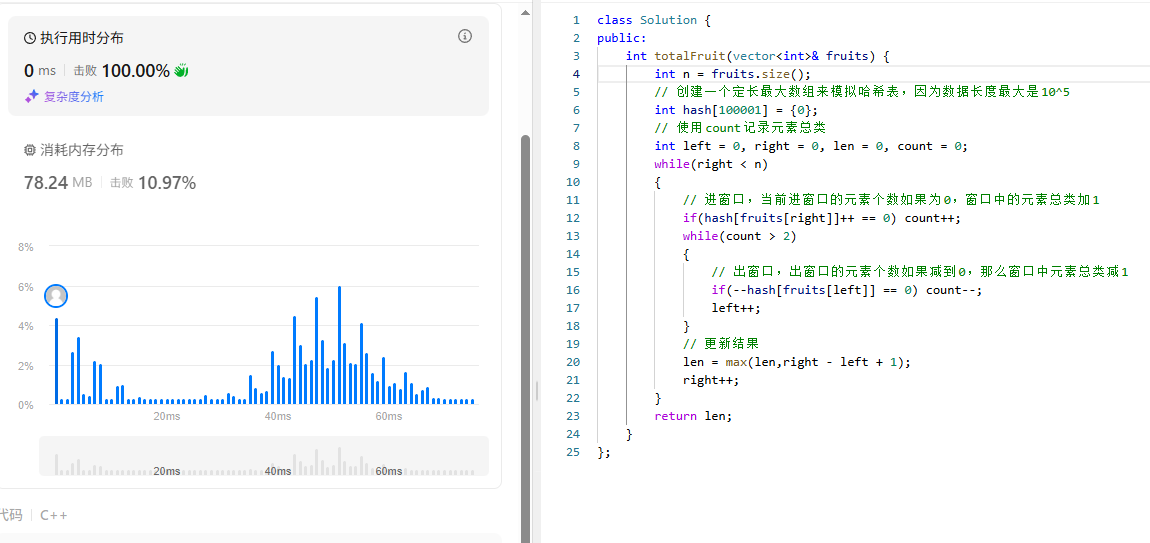

6.找到字符串中所有字⺟异位词

题目描述：

给定两个字符串 s 和 p，找到 s中所有 p的 异位词 的子串，返回这些子串的起始索引。不考虑答案输出的顺序。异位词 指由相同字⺟重排列形成的字符串（包括相同的字符串）。

异位词，说明要我们找一个固定长度连续的字符串，并且该字符串还要与p进行比较，那么这个题目妥妥的是滑动窗口加哈希了，是不是以为就“颗秒”了。

这里与我们上面写的滑动窗口有一些不同，这里的窗口大小是固定的，但是其实这反而降低了一点难度，因为我们只要每次出一个字符，再进一个字符，继而判断一下整个字符串是否为异位词记录下标，重复循环直到结束即可。

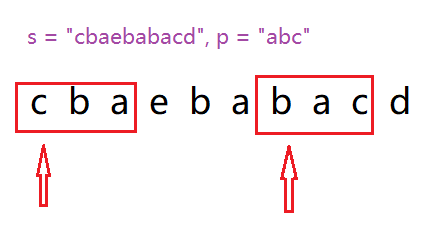
听起来还挺简单的吧，但是该题目与上面那个水果篮子不同的点在于，我们需要比较当前窗口与p中的所有元素，于是我们需要每次进窗口以后比较一下这个字符个数是否小于等于p中的元素个数，倘若是那么此次插入的个数是有效字符，win_kinds++。当窗口中的有效字符等于p中的元素个数，更新结果。

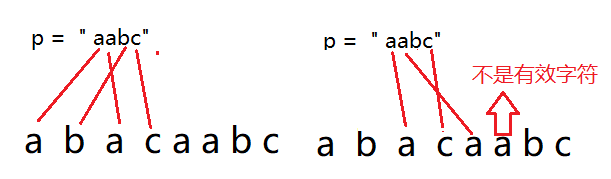
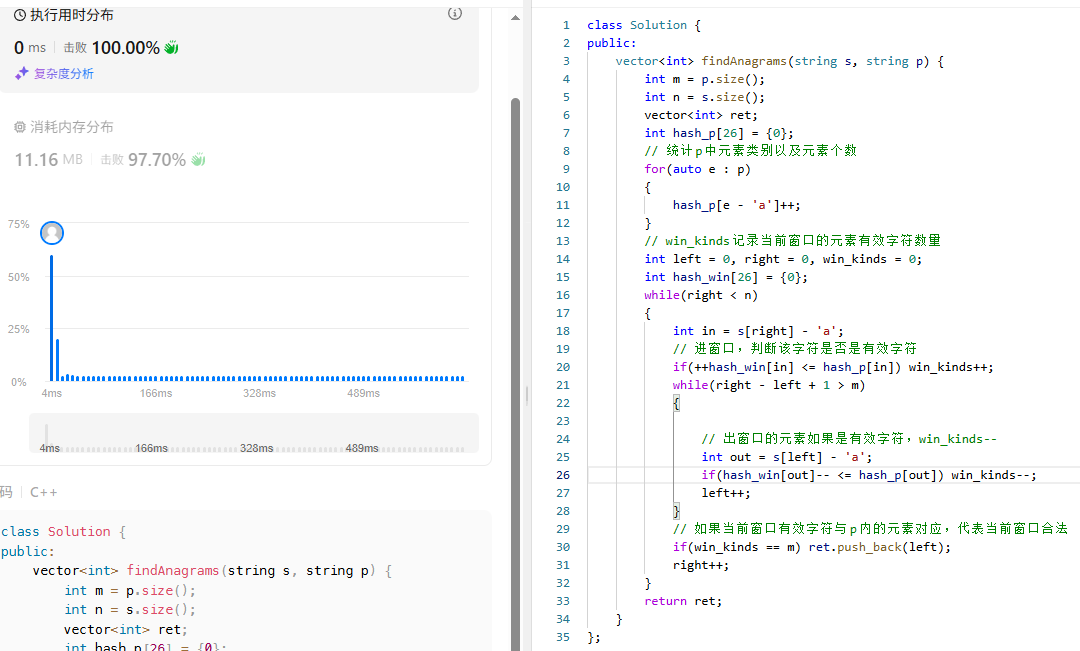
具体代码以及测试：

这里还是使用的数组模拟哈希表，把26个字母映射数组不同下标中。

注意：hash_win中存在但是hash_p中不存在的元素不会使win_kinds++，不会出现 0 = 0的情况，hash_win[in]此时一定大于0。

7.最小覆盖字串

题目描述：

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

注意：

• 对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
• 如果 s 中存在这样的子串，我们保证它是唯一的答案。

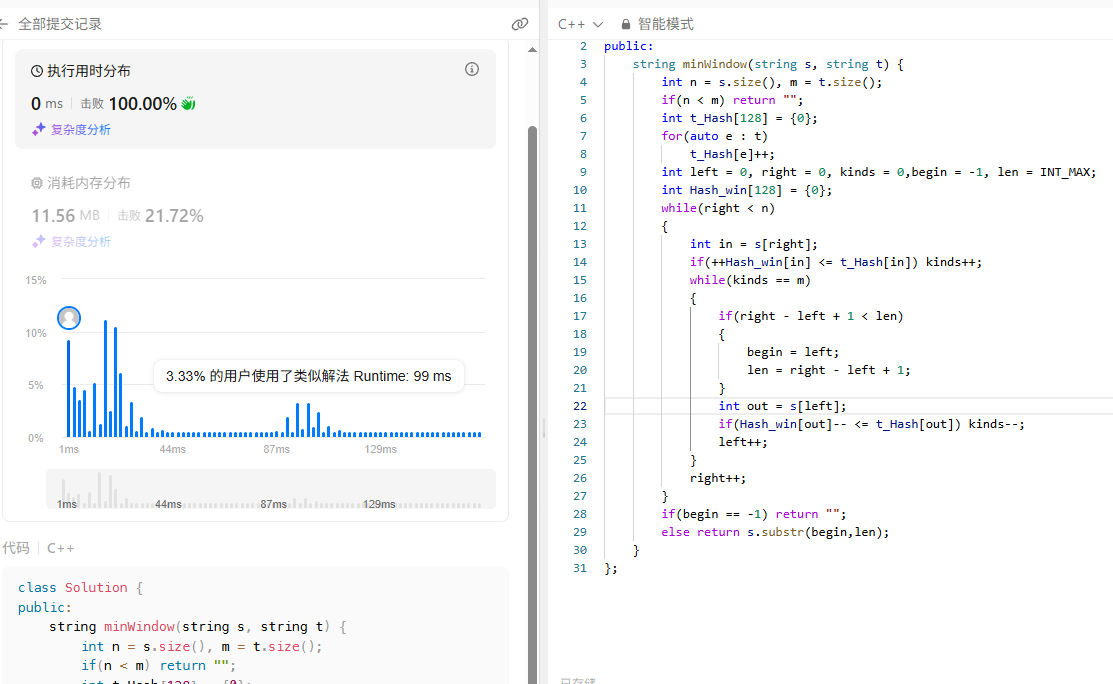
该题目与上面那种题目很接近，只不过此时需要返回的是一个子串，这个子串长度不一定和t的一样，即不是固定的窗口，但是原来大同小异，现在进窗口的条件改为了kinds == m，所以进窗口以后我们就要更新结果，然后再进行窗口的操作。由于出窗口的不一定是有效字符，所以直到kinds < m，才会跳出循环，在这个过程中我们也能找到这个区间中的一个最小子串。例如t = abc，有一段区间abdfgjabc，当窗口为abdfgjabc的时候kinds == m，然后左边一直会出窗口，直到最小的区间abc，再把a移出去，条件不满足循环结束。

具体代码以及测试：

三.总结

滑动窗口思想的大概步骤

1. 初始化窗口：确定窗口的起始位置和初始大小，通常运用两个指针（如左指针和右指针）来标记窗口的边界。

2. 扩展窗口：移动右指针，将新元素纳入窗口，直到窗口满足问题的特定条件（如包括所有目标元素、达到特定大小等）。

3. 收缩窗口：一旦窗口满足条件，尝试移动左指针，尽可能缩小窗口，同时保持条件成立，以找到最优解（如最小长度、最大和等）。

4. 更新结果：在每次窗口满足条件时，记录当前窗口的状态（如长度、元素和等），并根据问题要求更新全局最优解。

5. 重复步骤：继续扩展和收缩窗口，直到右指针遍历完整个数组。

滑动窗口思想的优势

• 时间复杂度低：滑动窗口通常能将时间复杂度从暴力解法的O(n^2)或O(n^3)降低到O(n)，因为它避免了重复计算，每个元素最多被访问两次（一次被右指针纳入窗口，一次被左指针移出窗口）。

• 空间效率高：滑动窗口通常只需要常数级别的额外空间（如几个指针变量），空间复杂度为O(1)，适用于处理大规模材料。

• 思路清晰：滑动窗口通过维护一个动态的窗口，将复杂的问题分解为容易的步骤，易于理解和实现。

• 适用性广泛通过：滑动窗口能够用于解决多种类型的问题，如子数组/子串难题、最优化问题（如最大和、最小长度）、存在性问题（如是否包含特定子串）等。

总结：

滑动窗口思想经过动态维护一个窗口来高效地处理线性数据结构中的子序列问题，具有时间复杂度低、空间效率高、思路清晰和适用性广泛等优势，是一种常用且有效的算法设计技巧。