深入解析：神经网络中的反向传播与梯度下降

文章目录

• • 1 引言：神经网络优化的核心挑战
  • 2 核心挑战一：反向传播和梯度下降的作用
  • • 2.1 神经网络训练的本质
    • 2.2 分工协作：为什么需要两个算法？
  • 3 核心问题二：反向传播和梯度下降的具体过程
  • • 3.1 梯度下降的数学原理
    • 3.2 反向传播：梯度的高效计算引擎
  • 4 核心障碍三：为什么梯度下降的方向损失一定减小？
  • • 4.1 泰勒展开的视角
    • 4.2 为什么是负梯度方向？
  • 5 核心问题四：链式法则的数学原理与实现
  • • 5.1 链式法则：反向传播的引擎
    • 5.2 一个具体的计算实例
    • 5.3 链式法则在神经网络中的一般形式
  • 6 总结与展望

---

带着问题阅读：
干什么用的？就是① 反向传播和梯度下降
② 反向传播和梯度的具体过程是什么样的？
③ 为什么梯度下降的方向，损失一定会减小？
什么样的？就是④ 反向传播中的链式法则是干什么的？它的数学原理是什么？实现过程是什么样的？最终的输出

1 引言：神经网络优化的核心挑战

在深度学习中，神经网络凭借学习数据中的复杂模式来执行各种智能任务。然而，这种学习能力并非与生俱来，而是通过一个关键的优化过程实现的。想象一下，大家要教一个新手投篮：他首先尝试投一次篮，观察球落点与目标的差距，然后分析误差来源（是手腕角度问题？手肘问题？还是腿部发力问题？），终于根据这个分析微调全身的动作。神经网络的学习过程与此惊人地相似。

反向传播和梯度下降正是这个"分析误差"和"微调动作"的数学实现。它们共同解决了神经网络训练的核心挑战：如何调整数百万甚至数十亿的参数，使得网络的预测结果与真实目标尽可能接近。下面，让我们通过一个整体框架来直观理解这两个算法如何协同工作：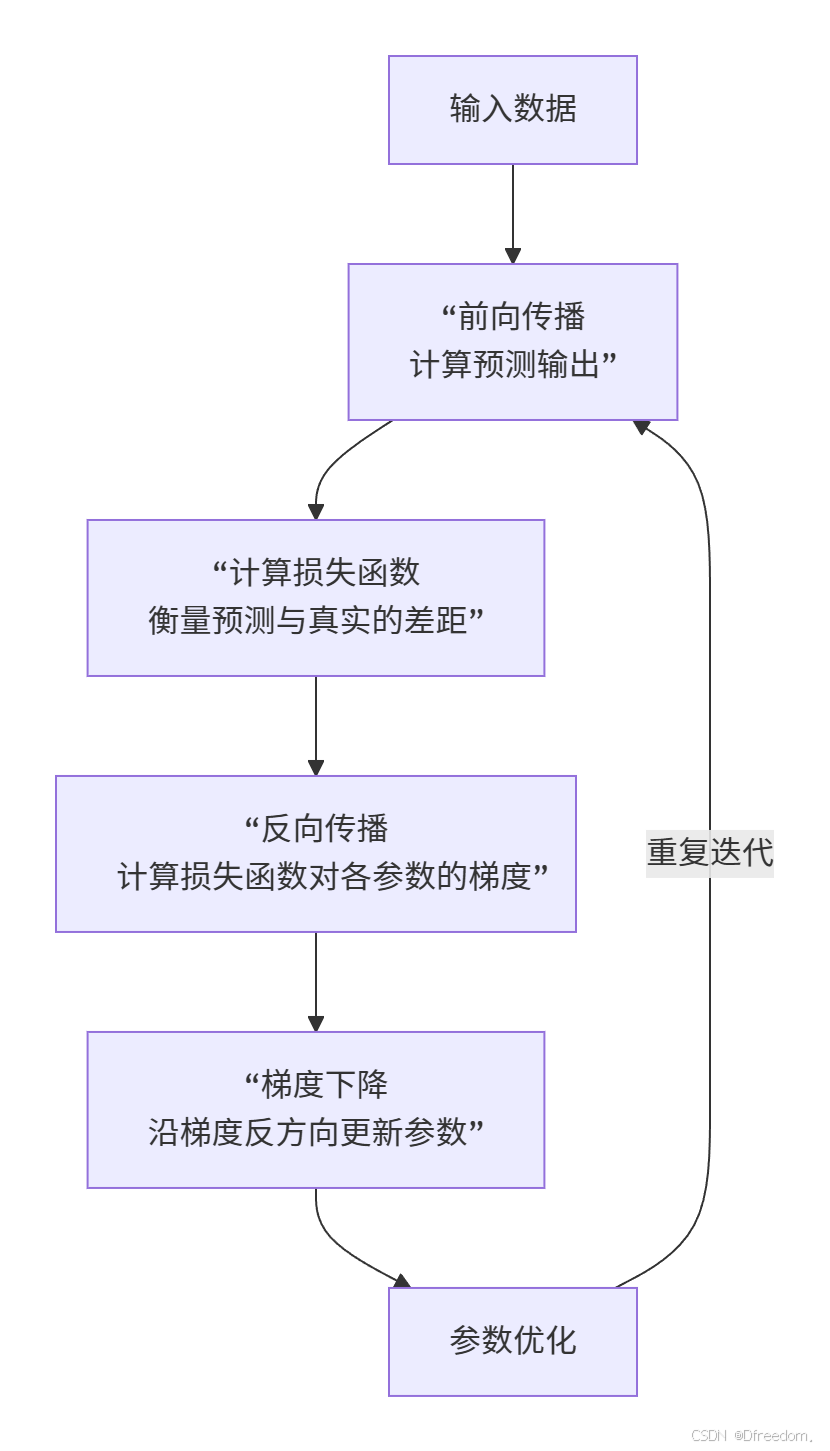

2 核心问题一：反向传播和梯度下降的作用

2.1 神经网络训练的本质

神经网络的学习过程本质上是一个优化问题。其核心目标是找到一组最优的权重(W)和偏置(b)参数，使得神经网络对于给定输入的预测输出与真实的期望输出之间的"差距"最小。

这个"差距"是通过一个可微的损失函数来量化的。例如，对于回归困难，常用均方误差；对于分类疑问，常用交叉熵损失。因此，训练神经网络的任务就转化为了一个数学任务：最小化损失函数。

2.2 分工协作：为什么必须两个算法？

要实现最小化损失函数该目标，需要解决两个关键问题：

1. 方向：如何确定每个参数(各个权重和偏置)的调整"方向"，是应该增加还是减少，才能使损失函数下降？
2. 幅度：每个参数具体应该调整"多大"的幅度？

反向传播和梯度下降算法，正是为了优雅地解决这两个问题而生的。

• 反向传播：解决"方向"问题。它通过计算损失函数对每个参数的梯度(偏导数)，来精确衡量每个参数对最终误差应负的"责任"。允许理解为一次全面的"责任追溯"。
• 梯度下降：解决"幅度"挑战。它根据反向传播计算出的梯度信息，按照一定的步长(学习率)更新参数，使损失函数向减小方向移动。

简单来说，反向传播负责计算梯度(指明方向)，梯度下降负责根据梯度更新参数(执行优化)。两者紧密协作，构成了现代深度学习模型训练的基础。

3 核心问题二：反向传播和梯度下降的具体过程

3.1 梯度下降的数学原理

梯度下降法的核心思想非常直观：若是我们想最快地到达山谷的最低点，一个有效的办法是沿着当前所在位置最陡峭的下坡方向其就是前进。在数学上，函数值下降最快的方向就梯度的反方向。

梯度下降的更新公式如下：

$${\theta }_{n+1}={\theta }_n-\eta \cdot \nabla J({\theta }_n)$$

• ${\theta }_n$：代表第n次迭代时当前的参数值。
• $\nabla J({\theta }_n)$：是损失函数$J$ 在 ${\theta }_n$ 处的梯度。
• $\eta$：是学习率，一个极其核心的超参数。它控制了每次参数更新的步长。
  • 学习率太小：收敛速度过慢，需要大量迭代。
  • 学习率太大：可能导致在最小值附近来回震荡，甚至发散。
• ${\theta }_{n+1}$：更新后的参数值。

3.2 反向传播：梯度的高效计算引擎

对于一个深度神经网络，其参数数量可能达到数百万甚至数十亿。这就引出了关键问题：如何高效地计算损失函数对于每一个参数的梯度(即偏导数)？这就是反向传播算法大显身手的地方。

反向传播是"误差反向传播"的简称，它是一种基于链式法则的高效算法，用于计算神经网络中每个参数的梯度。其核心过程如下：

1. 前向传播：输入数据从网络底层流向顶层，最终得到预测输出，并计算总损失。在此过程中，系统会缓存每一层的线性计算结果(z)和激活输出(a)，因为它们将在反向传播中被重复使用。
2. 误差反向传播：这是反向传播的核心。
   • 输出层：首先计算损失函数$L$对网络最终输出$a^{[输出层]}$ 的梯度 $\frac{\partial L}{\partial a^{[输出层]}}$。这个梯度直接反映了预测值与真实值的初始误差。
   • 层层反传：然后，利用链式法则，将误差梯度从后一层传递到前一层。具体来说，计算第$l$层的梯度需要用到第$l+1$层已经计算好的梯度。公式可以简化为：
     $$d{Z}^{[l]}=d{A}^{[l]}\cdot g^{\prime [l]}(Z^{[l]})$$ (其中 $g^{\prime }$是激活函数的导数)
     $$d{W}^{[l]}=\frac{1}{m}\cdot d{Z}^{[l]}\cdot (A^{[l-1]}{)}^T$$
     $$d{b}^{[l]}=\frac{1}{m}\cdot \sum d{Z}^{[l]}$$
3. 参数更新：在得到所有参数的梯度$d{W}^{[l]}$ 和 $d{b}^{[l]}$后，就可以使用梯度下降公式同时更新所有参数：
   $$W^{[l]}=W^{[l]}-\eta \cdot d{W}^{[l]}$$
   $$b^{[l]}=b^{[l]}-\eta \cdot d{b}^{[l]}$$

下面的序列图直观展示了一次完整迭代中，前向传播、反向传播和参数更新三个过程如何协同工作：

4 核心问题三：为什么梯度下降的方向损失一定减小？

梯度下降法之所以实用，其根本原因在于数学上的严格保证。简单来说，沿着梯度反方向(负梯度方向)前进，是损失函数在当前点附近下降最快的方向。下面我们通过泰勒展开来深入理解这一点。

4.1 泰勒展开的视角

要理解梯度下降，一个强大的工具是一阶泰勒展开。它允许我们在当前参数点附近对损失函数进行线性近似。

假设在时刻 $t$，我们的模型参数为${\theta }_t$，损失函数为$L({\theta }_t)$。我们想知道，如果将参数做一个小小的变动$\Delta \theta$，损失函数会如何变化。根据一阶泰勒展开，新的损失$L({\theta }_t+\Delta \theta )$可以近似为：

$$L({\theta }_t+\Delta \theta )\approx L({\theta }_t)+\nabla L({\theta }_t{)}^T\Delta \theta$$

这里：

• $L({\theta }_t)$是当前的损失值，一个已知的数。
• $\nabla L({\theta }_t)$是损失函数在当前点的梯度，它是一个向量，指向函数值增长最快的方向。
• $\Delta \theta$是参数的变动量。

大家的目标是让新的损失$L({\theta }_t+\Delta \theta )$小于当前的损失 $L({\theta }_t)$要让等式右边第二项就是。从上面的近似公式看，就$\nabla L({\theta }_t{)}^T\Delta \theta$ 为负数，且其绝对值越大，损失下降得就越多。

4.2 为什么是负梯度方向？

从向量内积的角度看，$\nabla L({\theta }_t{)}^T\Delta \theta =\Vert \nabla L({\theta }_t)\Vert \Vert \Delta \theta \Vert \cos \varphi$(其中 $\varphi$是梯度向量和参数变化向量之间的夹角)。为了使这个内积为负且最小(即损失下降最多)，$\cos \varphi$需要取最小值 -1，这对应着$\varphi =180^{\circ }$，即 $\Delta \theta$的方向与梯度方向完全相反，也就是负梯度方向$(-\nabla L({\theta }_t))$。

因此，最理想的变化量$\Delta \theta$应该与负梯度方向成正比：$\Delta \theta =-\alpha \nabla L({\theta }_t)$ ($\alpha >0$)。

将这个 $\Delta \theta$代入泰勒展开式：
$$L({\theta }_t+\Delta \theta )\approx L({\theta }_t)+\nabla L({\theta }_t{)}^T(-\alpha \nabla L({\theta }_t))=L({\theta }_t)-\alpha \Vert \nabla L({\theta }_t){\Vert }^2$$

由于学习率 $\alpha >0$，梯度模的平方$\Vert \nabla L({\theta }_t){\Vert }^2\ge 0$，所以 $\alpha \Vert \nabla L({\theta }_t){\Vert }^2>0$，从而有：
$$L({\theta }_t+\Delta \theta )<L({\theta }_t)$$

这就从数学上严格地证明了，只要沿着负梯度方向更新参数，并且学习率$\alpha$足够小(以满足泰勒展开近似的准确性)，损失函数的值就一定会在下一次迭代中变小。

5 核心困难四：链式法则的数学原理与实现

5.1 链式法则：反向传播的引擎

链式法则是微积分中用于求解复合函数导数的法则，它是反向传播算法能够高效计算所有参数梯度的数学基础。对于函数$Y=f(g(x))$，$Y$ 关于 $x$通过的导数能够分解为：$\frac{dY}{dx}=\frac{dY}{du}\cdot \frac{du}{dx}$，其中 $u=g(x)$。

在神经网络中，损失函数$L$是网络每一层输出的复合函数。因此，计算损失函数$L$对某一层参数$W^{[l]}$的梯度，就要求通过链式法则，将来自后面层(更靠近输出层的层)的误差梯度，一层一层地反向传递回来。

链式法则的核心目标是为了高效且系统地计算出最终损失函数对网络中所有参数(包括第一层的权重和偏置)的梯度(偏导数)。

5.2 一个具体的计算实例

让我们依据一个非常简单的例子来直观感受链式法则的传播过程。这个例子模拟了神经网络中一个基本计算单元的前向和反向传播。

假设我们有一个简单的复合函数：$f(x,y,z)=(x+y)\cdot z$
为了清晰起见，大家引入一个中间变量$q=x+y$，所以 $f=q\cdot z$。

现在，给定输入值：$x=-2$, $y=5$, $z=-4$。

前向传播(计算最终输出)：

1. 计算 $q=x+y=-2+5=3$
2. 计算 $f=q\cdot z=3\cdot (-4)=-12$

反向传播(应用链式法则计算梯度)：
我们的目标是计算$f$对每个输入变量的梯度。

1. 计算 $f$ 对 $z$ 和 $q$的梯度(输出层)

   • 梯度 $\frac{\partial f}{\partial z}$：$f=q\cdot z$ 对 $z$ 的偏导数是 $q$。代入 $q=3$，得 $\frac{\partial f}{\partial z}=3$。
   • 梯度 $\frac{\partial f}{\partial q}$：$f=q\cdot z$ 对 $q$ 的偏导数是 $z$。代入 $z=-4$，得 $\frac{\partial f}{\partial q}=-4$。

2. 计算 $f$ 对 $x$ 和 $y$的梯度(继续反向传播)

   • 梯度 $\frac{\partial f}{\partial x}$：因为 $q=x+y$，所以 $\frac{\partial q}{\partial x}=1$。根据链式法则：$\frac{\partial f}{\partial x}=\frac{\partial f}{\partial q}\cdot \frac{\partial q}{\partial x}$。代入 $\frac{\partial f}{\partial q}=-4$ 和 $\frac{\partial q}{\partial x}=1$，得 $\frac{\partial f}{\partial x}=(-4)\cdot 1=-4$。
   • 梯度 $\frac{\partial f}{\partial y}$：计算过程完全相同，因为$\frac{\partial q}{\partial y}=1$：$\frac{\partial f}{\partial y}=\frac{\partial f}{\partial q}\cdot \frac{\partial q}{\partial y}=(-4)\cdot 1=-4$。

最终，我们得到了所有参数的梯度：$\frac{\partial f}{\partial x}=-4$, $\frac{\partial f}{\partial y}=-4$, $\frac{\partial f}{\partial z}=3$。

这个简单的例子完美演示了反向传播的核心机制：前向传播计算预测值，反向传播利用链式法则，将梯度乘以路径上的局部梯度，一步步反向传递，高效地计算出所有参数的梯度。

5.3 链式法则在神经网络中的一般形式

在多层神经网络中，链式法则的应用如下面的有向图所示，展示了误差梯度如何从最终输出开始，凭借链式法则沿着网络结构反向传播，最终到达网络的输入层：

例如，对于输出层的权重$W^{[L]}$，其梯度计算为：
$$\frac{\partial L}{\partial W^{[L]}}=\frac{\partial L}{\partial a^{[L]}}\cdot \frac{\partial a^{[L]}}{\partial z^{[L]}}\cdot \frac{\partial z^{[L]}}{\partial W^{[L]}}$$
其中，$a^{[L]}$是输出层激活值，$z^{[L]}$是输出层线性输出。

对于更前面层的参数，链式会更长，但原理相同，从而高效地计算出损失函数对网络中每个参数的梯度。

6 总结与展望

深度学习中最核心、最基础的算法。它们的精妙配合使得训练艰难的深层神经网络成为可能：就是反向传播和梯度下降

• 梯度下降献出了一个通用的优化框架，其数学原理(泰勒展开)保证了沿负梯度方向更新参数能有效降低损失函数值。
• 反向传播则提供了一种高效计算网络中数百万个参数梯度的方法，其核心数学应用是链式法则。

然而，在实际应用中，为了获得更好、更快的训练效果，研究者们提出了许多优化技巧和高级优化器，例如：

• 动量法：协助加速收敛并抑制振荡。
• 自适应学习率算法：如Adam，能够自适应地调整每个参数的学习率。
• 批归一化：经过稳定每层的输入分布来加速训练。

---

感谢阅读！如果本文对您有所帮助，请不要吝啬您的【点赞】、【收藏】和【评论】，这将是我持续创作优质内容的巨大动力。