(十二)随机预言机回顾 - 指南
来到最有意思的一节,随机预言机。我在写安全证明的时候时常会遇到它,感觉随机预言机很神秘,知道他能提取输入,但是不知道为什么它可以。
随机预言机(记作O \mathcal OO)通常利用理想哈希函数H HH来表示,其输出在输出空间中呈随机且均匀分布。
对于一个所提方案在随机预言机下的安全证明意味着在该方案中要有至少一个哈希函数被当作随机预言机。本篇博客介绍在安全证明中如何使用随机预言机。
1.使用随机预言机的安全证明
假设一个所提方案使用哈希函数作为原语之一。能够使用以下方式表示这个方案:
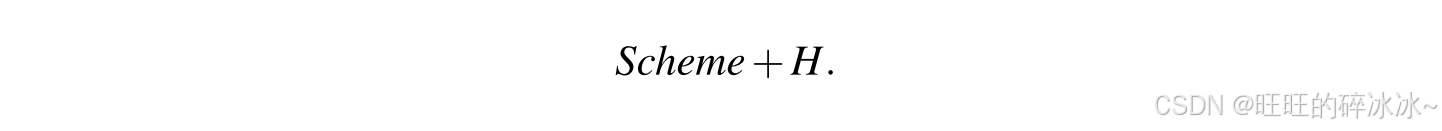
简单来说,一个使用随机预言机的安全证明,可以表示如下: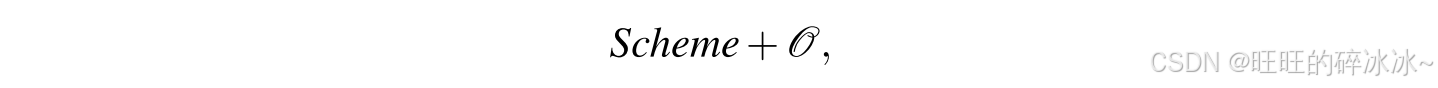
这里的哈希函数H HH被设置为一个随机预言机O \mathcal OO
也就是说,我们分析的不是Scheme+H HH的安全性,而是Scheme+O \mathcal OO的安全性,并认为若Scheme+O \mathcal OO安全则Scheme+H HH不同的。二者之间的差距在这篇论文[就是也安全。值得注意的是,随机预言机与哈希函数在安全规约中Separating random oracle proofs from complexity theoretic proofs: The non-committing encryption case]中有所讨论。
要证明所提方案在随机预言机模型下的安全性,至少需要一个哈希函数作为随机预言机。并不需要所有的哈希函数均当作随机预言机。
为了保证与不可区分模拟在概念上的一致性,假定随机预言机模型下的真实方案也是Scheme+O \mathcal OO组成。否则敌手能够很快区分出采用随机预言机的模拟方案和使用哈希函数的真实方案。
2.哈希函数VS随机预言机
哈希函数与随机预言机在安全规约中的不同之处:
- 知识。给定一个任意字符串x xx,如果H HH是哈希函数,敌手知道H HH的函数算法,因此敌手知道如何计算H ( x ) H(x)H(x)。然而,若是H HH是一个随机预言机,除非敌手向随机预言机问询过x xx,否则它不知道H ( x ) H(x)H(x)是什么。
- 输入。哈希函数与随机预言机有相同的输入空间,它独立于哈希函数的定义。尽管输入到哈希函数的数量是指数大的,但输入到随机预言机的数量是多项式大小的。这是因为随机预言机只接受多项方式次数的问询,因此随机预言机的输入大小就是多项式大小。
- 随即且均匀分布的。就是输出。哈希函数与随机预言机有相同的输出空间,这独立于哈希函数的定义。给定一个输入,一个哈希函数的输出被输入和哈希函数算法决定。但给定一个输入,对于随机预言机的输出是由模拟器定义的,它可以控制随机预言机。但是随机预言机的输出必须
- 表示。一个哈希函数可以被当做是从一个输入空间到输出空间的映射,该映射可以通过哈希函数算法计算出来。随机预言机可视为一种虚拟哈希函数,其仅由输入输出对构成的列表表示。该预言机本身不包含任何定义映射关系的规则或算法,只需确保所有输出均为随机且相互独立。如下图所示:

随机预言机对于编写安全规约是有帮助的。原因在于,模拟器允许控制和选择任何看似随机的输出,这既有助于模拟器结束模拟,又能迫使敌手发起有效攻击。因此,人们普遍认为,随机预言机模型下的安全性证明比非随机预言机模型下的证明更为简单。
3.哈希表
在带随机预言机的安全规约中,对于预言机的问询和回应正如上图所示,输入和输出是被敌手知道的。输出可以被模拟器自适应计算,他们是随机且独立的。如何计算输出应该被记录下来,因为这对于模拟器编写安全规约是有协助的。设x xx是一个问询,y yy是响应,S SS是用来计算y yy的秘密状态字。模拟器回应问询x xx的相应y = H ( x ) y=H(x)y=H(x)之后,模拟器应该把元组( x , y , S ) (x,y,S)(x,y,S)添加到哈希列表中,即为L \mathcal LL。
哈希表被模拟器创建,包含输入,输出,以及相关状态字S SS。哈希表应该满足以下条件:
- 在问询之前,哈希表是空的
- 所有问询都应该被添加到哈希表中
- 不知道的就是秘密状态字敌手
在计算 y yy时如何选择 S SS完全取决于所提出的方案及其安全性归约。对于某些加密方案的安全性归约,y yy可以不依赖秘密状态而随机选取。
4.在随机预言机模型下如何编写安全规约
对于一个在随机预言机模型下的安全规约,模拟器应在模拟中额外添加一个称为H-Query的阶段(通常位于Setup阶段之后),用于描述哈希查询与响应。需注意该阶段仅出现在安全归约过程中,而不应出现在安全模型中。
H-Query. 敌手在该阶段会做哈希问询。模拟器需要准备一个哈希表记录敌手所有的问询和响应,注意,该哈希表开始时置为空。
对于一个随机预言机的问询x xx,如果x xx在哈希表中已经存在,那么模拟器按照表中对应的值进行响应。否则,模拟器生成一个随机的秘密状态字S SS,使用S SS去计算哈希输出y yy。最后把( x , y , S ) (x,y,S)(x,y,S)添加到哈希表中。
如果在随机预言机模型下,有多个哈希表被设计,那么模拟器必须描述如何编程每一个哈希表。在随机预言机模型下,即使敌手在赢得游戏后,仍可以随时向随机预言机发起问询。
为了确保随机预言机允许支援模拟器编写模拟,模拟器应该以自适应的方式产生所有的输出,举个例子,比如说签名模拟,私钥模拟。
如何自适应回应敌手的所有问询,是独立于所提方案,底层困难挑战以及安全规约的。
5.预言机响应及概率分析
设哈希函数H HH为一个随机预言机。下面分析一个预言机响应例子及分析它成功的概率。
H-Query。模拟器准备一个哈希表L \mathcal LL来记录所有的问询和响应,哈希表初始为空。
对于一个问询x xx,如果x xx已经在哈希表中,模拟器按照对应结果进行响应即可。否则,模拟器工作如下:
- 模拟器选择一个随机秘密值z zz和一个秘密比特c ∈ { 0 , 1 } c\in\{0,1\}c∈{0,1}去计算y yy。S = ( z , c ) S=(z,c)S=(z,c)是计算y yy的秘密状态字。
- 模拟器接下来设置H ( x ) = y H(x)=yH(x)=y,把y yy发给敌手。
- 最后,模拟器添加( x , y , z , c ) (x,y,z,c)(x,y,z,c)到哈希表中。
至此完成了模拟中随机预言机执行的描述。假设向随机预言机发起q H q_HqH次哈希查询,则哈希表由如下q H q_HqH个元组构成:
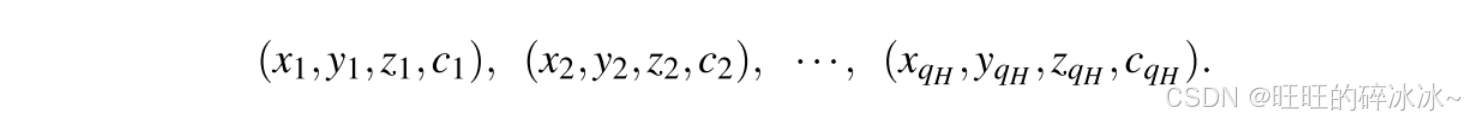
设敌手不知道( z 1 , c 1 ) , ( z 2 , c 2 ) , ( z 3 , c 3 ) , … , ( z q H , c q H ) (z_1,c_1),(z_2,c_2),(z_3,c_3),\dots,(z_{q_H},c_{q_H})(z1,c1),(z2,c2),(z3,c3),…,(zqH,cqH),从q H q_HqH次问询中,敌手自适应选择q + 1 q+1q+1次问询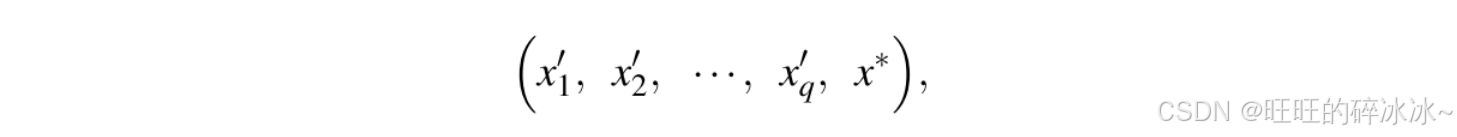
q + 1 ≤ q H q+1\leq q_Hq+1≤qH。令c 1 ′ , c 2 ′ , … , c q ′ , c ∗ c_1',c_2',\dots,c_q',c^*c1′,c2′,…,cq′,c∗是选择哈希问询的选择比特。那么成功概率的计算,行表示如下:
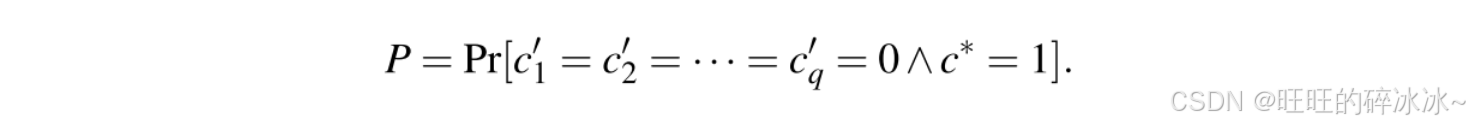
需要强调的是,一旦所有c i c_ici均被攻击者获知,该概率便无法计算。因此假设攻击者在初始阶段并不知晓所有c i c_ici。
这个概率在许多安全证明中都会出现。例如在随机预言机模型下数字签名的安全证明过程中,安全归约的设计使得消息x xx的签名在 c = 0 c =0c=0时可模拟,而在c = 1 c =1c=1时可归约。设敌手首先问询消息x 1 ′ , x 2 ′ , … , x q ′ x_1',x_2',\dots,x_q'x1′,x2′,…,xq′的签名,然后返回一个x ∗ x^*x∗的伪造签名。成功模拟的概率就等于:
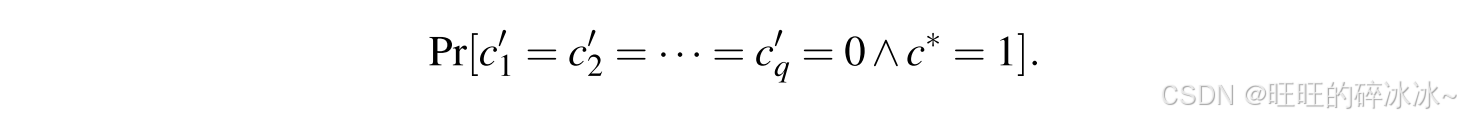
上述成功概率取决于c i c_ici的选取方法。此处介绍两种方案:第一种方案易于理解,但概率相对较小,且损失因子与总哈希查询次数q H q_HqH呈线性关系;第二种方案稍显复杂,但其成功概率高于第一种,且损失因子仅与选定哈希查询次数q qq呈线性关系。
下面分别介绍:
- 在第一个手段中,模拟器随机选择i ∗ ∈ [ 1 , q H ] i^*\in[1,q_H]i∗∈[1,qH],然后猜测敌手输出的第i ∗ i^*i∗次问询的结果x ∗ x^*x∗。对于一个问询x i x_ixi,模拟器设置:
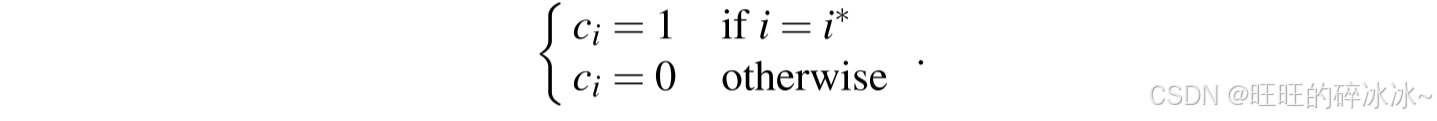 在此设定下,P PP等价于成功猜测哪个查询被选为x ∗ x^*x∗。由于敌手进行q H q_HqH次查询,且其中一条查询被选作x ∗ x^*x∗,因此 P = 1 / q H P =1/q_HP=1/qH。成功概率与所有哈希查询次数呈线性关系。
在此设定下,P PP等价于成功猜测哪个查询被选为x ∗ x^*x∗。由于敌手进行q H q_HqH次查询,且其中一条查询被选作x ∗ x^*x∗,因此 P = 1 / q H P =1/q_HP=1/qH。成功概率与所有哈希查询次数呈线性关系。 - 在第二种方法中,模拟器会猜测多个查询作为潜在的x ∗ x^*x∗以提高成功概率。具体而言,模拟器以概率P b P_bPb生成b i = 0 b_i=0bi=0,以概率1 − P b 1-P_b1−Pb生成b i = 1 b_i=1bi=1(其中b i ∈ { 0 , 1 } b_i \in \{0,1\}bi∈{0,1})。对于查询x i x_ixi,模拟器设定
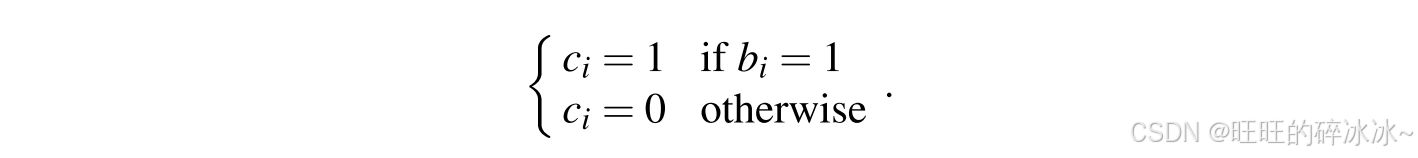 由于所有 b i b_ibi均按概率 P b P_bPb选取,因此大家有
由于所有 b i b_ibi均按概率 P b P_bPb选取,因此大家有
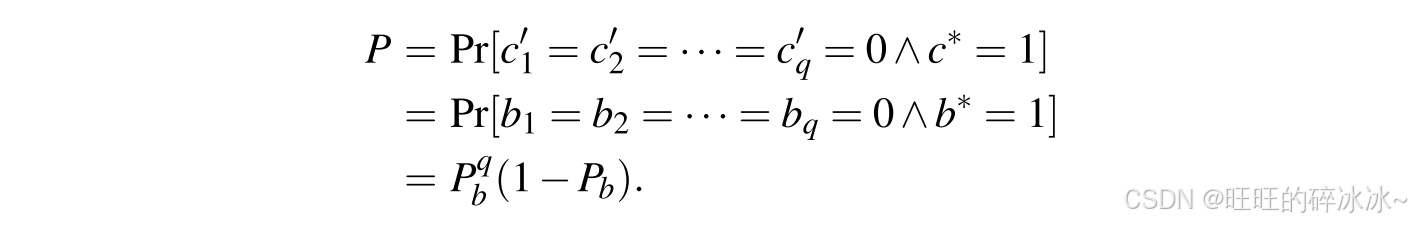 该值最大为P b = 1 − 1 q + 1 P_b=1-\frac{1}{q+1}Pb=1−q+11,当( 1 + 1 q ) q ≃ e (1+\frac{1}{q})^q \simeq e(1+q1)q≃e时,P ≃ 1 e q P\simeq\frac{1}{eq}P≃eq1。该成功概率与所选哈希查询次数呈线性关系,而非所有哈希查询的总次数。
该值最大为P b = 1 − 1 q + 1 P_b=1-\frac{1}{q+1}Pb=1−q+11,当( 1 + 1 q ) q ≃ e (1+\frac{1}{q})^q \simeq e(1+q1)q≃e时,P ≃ 1 e q P\simeq\frac{1}{eq}P≃eq1。该成功概率与所选哈希查询次数呈线性关系,而非所有哈希查询的总次数。
在安全证明中,通常认为q H q_HqH远大于 q qq(例如 q H = 2 60 q_H =2^{60}qH=260对比 q = 2 30 q =2^{30}q=230)。因此,第二种方法的成功概率高于第一种。然而,第一种途径在理解上比第二种更为简洁。本书所选方案的安全证明中,当安全归约要求在这两种技巧中选择其一时,我们始终采用第一种方法。若需减小归约损失,可自然地改用第二种方法对安全证明进行修正。
6.随机预言机的利用总结
总结一下安全证明中随机预言机的使用,尤其是在数字签名与加密方案中。
- 随机预言机有用并不是因为它的输出是随机且均匀的,而是因为敌手必须向随机预言机问询x xx,以此来得到输出H ( x ) H(x)H(x),输出的计算完全由模拟器控制。
- 随机预言机就是一个理想的哈希函数。但是在模拟的时候并不需要去构造这个理想的哈希函数。在安全规约中,模拟器的重要工作是去思考如何回应敌手的每次问询。
- 模拟器可以自适应选择任何随机元素作为一个问询的回应,只要在敌手的视图看来是随机的即可。这一技巧对于"先哈希后签名"(hash-then-sign)数字签名的安全性证明非常有用。具体而言,我们利用编程方式设定H ( m ) H(m)H(m),使得H ( m ) H(m)H(m)对应的签名要么可模拟,要么可归约。
- 哈希表刚创建的时候它是空的,但敌手许可在敌手问询x xx之前预定义元组( x , H ( x ) , s ) (x,H(x),s)(x,H(x),s)到哈希表中。当一个签名需要H ( x ) H(x)H(x),而x xx并没有被敌手问询过时,这一技巧很有用。
- 关于x xx的秘密状态S SS可用于以下场景:在数字签名中计算x xx的签名;在基于身份的加密中生成x xx的私钥;或在无需知晓对应私钥的情况下执行解密操作。
- 若破解方案必须使用特定对( x , H ( x ) ) (x,H(x))(x,H(x)),则敌手必然已向随机预言机查询过x xx。这一性质在基于计算困难性假设的加密方案安全性证明中至关重要。
- 为简化安全性证明,我们假设模拟器在模拟前已获知敌手对随机预言机查询次数的上限。该假设在概率计算中具有重要作用。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号