【LeetCode 704 & 34_二分查找】二分查找 & 在排序数组中查找元素的第一个和最后一个位置 - 指南

场景应用

在算法学习中，二分查找是一种高效的查找算法，其时间复杂度为 $O (l o g n)$ ，适用于有序数组的查找场景。在实际场景中，当只需判断目标值是否存在于有序数组中，且数组内元素唯一时，用最简单的基础二分查找就足够，比如在按学号有序排列的唯一学生ID数组中查找某学生是否存在、在无重复的商品编码有序列表中检索指定编码是否存在；而当有序数组中存在重复的目标值，且需要确定目标值的范围边界时，就需要用查找左右边界的二分查找，比如在按时间戳排序的重复打卡记录中找某员工首次和末次打卡的位置、在成绩有序数组中找某分数出现的起始和结束排名、在商品销量统计的有序数组中找某一销量值对应的首个和最后一个商品下标。
在这里插入图片描述

场景应用

一、二分查找

1.1 题目链接

704. 二分查找【点击进入】

1.2 题目描述

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

提示：

你可以假设 nums 中的所有元素是不重复的。
n 将在 [1, 10000]之间。
nums 的每个元素都将在 [-9999, 9999]之间。

1.3 题目示例

示例 1：

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2：

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

1.4 算法思路

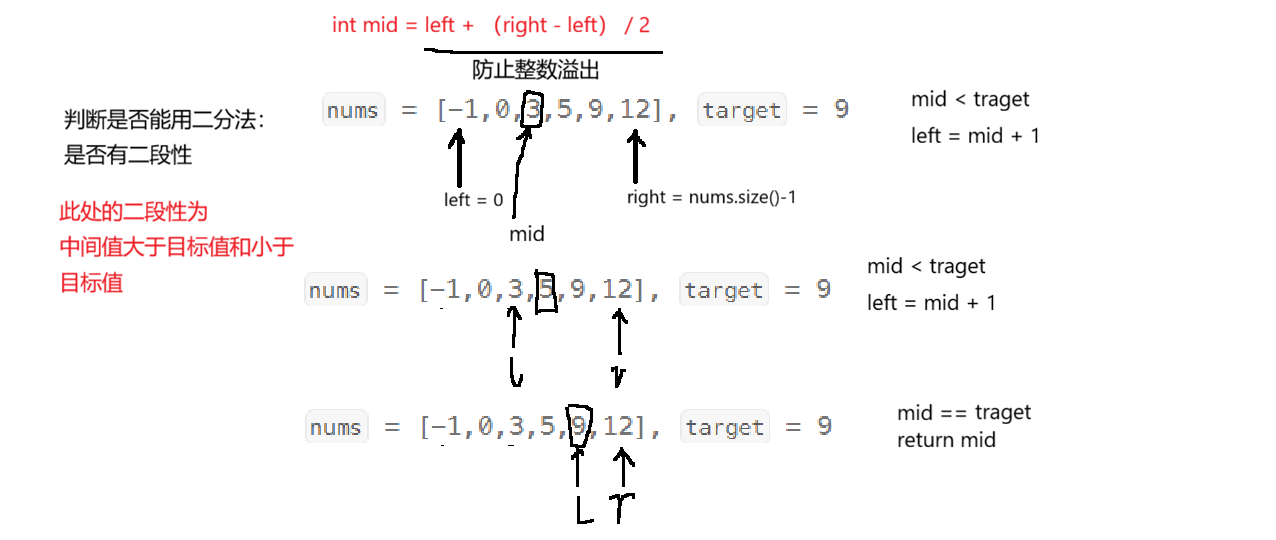
二分查找的核心是利用数组的有序性，不断缩小搜索范围。具体思路如下：

初始化两个指针，left 指向数组起始位置（下标为0），right 指向数组末尾位置（下标为nums.size() - 1）。
在 left <= right 的条件下，计算中间位置 mid，计算公式为 mid = left + (right - left) / 2，该写法可避免 left + right 导致的整数溢出。
比较 nums[mid] 与 target 的大小：
- 若 nums[mid] == target，找到目标值，直接返回 mid。
- 若 nums[mid] < target，说明目标值在右半部分，将 left 更新为 mid + 1。
- 若 nums[mid] > target，说明目标值在左半部分，将 right 更新为 mid - 1。
若循环结束仍未找到目标值，返回 -1。

> 此处可插入二分查找基础流程示意图

1.5 核心代码

class Solution {
public:
int search(vector<int>& nums, int target) {
  int left = 0;
  int right = nums.size()-1;
  while(left <= right)
  {
  int mid = left + (right - left) / 2;
  if(nums[mid] < target)
  left = mid + 1;
  else if(nums[mid] > target)
  right = mid - 1;
  else
  return mid;
  }
  return -1;
  }
  };

1.6 示例测试（总代码）

为了验证代码的正确性，我们可以编写测试代码，代入题目示例进行测试：

#include <iostream>
  #include <vector>
    using namespace std;
    class Solution {
    public:
    int search(vector<int>& nums, int target) {
      int left = 0;
      int right = nums.size()-1;
      while(left <= right)
      {
      int mid = left + (right - left) / 2;
      if(nums[mid] < target)
      left = mid + 1;
      else if(nums[mid] > target)
      right = mid - 1;
      else
      return mid;
      }
      return -1;
      }
      };
      int main() {
      // 示例1测试
      vector<int> nums1 = {-1, 0, 3, 5, 9, 12};
        int target1 = 9;
        Solution s;
        int result1 = s.search(nums1, target1);
        cout << "示例1输出：" << result1 << endl; // 预期输出4
        // 示例2测试
        vector<int> nums2 = {-1, 0, 3, 5, 9, 12};
          int target2 = 2;
          int result2 = s.search(nums2, target2);
          cout << "示例2输出：" << result2 << endl; // 预期输出-1
          return 0;
          }

二、在排序数组中查找元素的第一个和最后一个位置

2.1 题目链接

34. 在排序数组中查找元素的第一个和最后一个位置【点击进入】

2.2 题目描述

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

进阶：你可以设计并实现时间复杂度为 $O (l o g n)$ 的算法解决此问题吗？

提示：

0 <= nums.length <= 10^5
-10^9 <= nums[i] <= 10^9
nums 是一个非递减数组
-10^9 <= target <= 10^9

2.3 题目示例

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：

输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：

输入：nums = [], target = 0
输出：[-1,-1]

2.4 算法思路

本题需要找到目标值在有序数组中的第一个和最后一个位置，依然可以使用二分查找的思想，分别查找左边界和右边界：

查找左边界：
- 初始化 left = 0，right = nums.size() - 1。
- 循环条件为 left < right，计算 mid = left + (right - left) / 2。
- 若 nums[mid] < target，说明左边界在右半部分，更新 left = mid + 1；否则更新 right = mid。
- 循环结束后，检查 nums[left] 是否等于 target，若不等于则说明数组中无目标值，返回 [-1, -1]。
查找右边界：
- 重新初始化 left = 0，right = nums.size() - 1。
- 循环条件为 left < right，计算 mid = left + (right - left + 1) / 2（加1是为了避免死循环）。
- 若 nums[mid] <= target，说明右边界在右半部分，更新 left = mid；否则更新 right = mid - 1。
最终返回左边界和右边界组成的数组。

查找左边界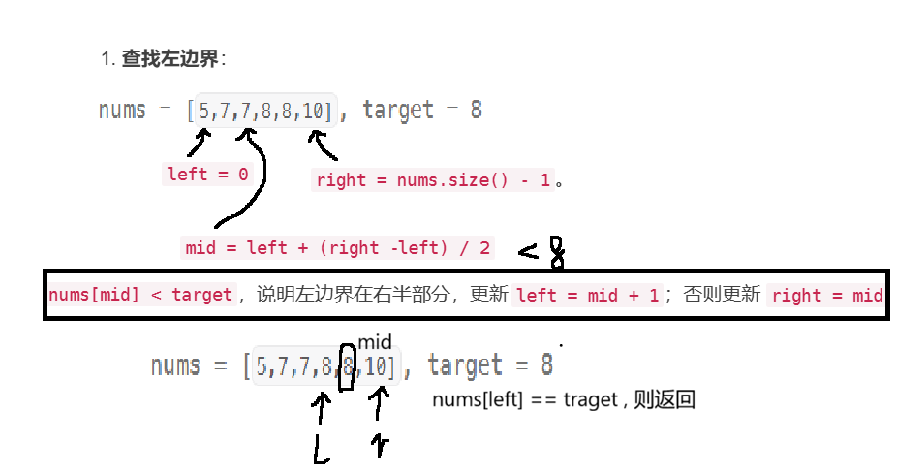
在这里插入图片描述
查找右边界

2.5 核心代码

class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
  if(nums.size() == 0) return{-1,-1};
  int begin = 0;
  int left = 0;
  int right = nums.size() -1 ;
  //找左端点
  while(left < right)
  {
  int mid = left + (right - left) / 2;
  if(nums[mid] < target) left = mid + 1;
  else right = mid;
  }
  if(nums[left] == target) begin = left;
  else return {-1,-1};
  //找右端点
  left = 0,right = nums.size()-1;
  while(left < right)
  {
  int mid = left + (right - left + 1) / 2;
  if(nums[mid] <= target) left = mid;
  else right = mid - 1;
  }
  return {begin,right};
  }
  };

2.6 示例测试（总代码）

编写测试代码，验证上述核心代码的正确性：

#include <iostream>
  #include <vector>
    using namespace std;
    class Solution {
    public:
    vector<int> searchRange(vector<int>& nums, int target) {
      if(nums.size() == 0) return{-1,-1};
      int begin = 0;
      int left = 0;
      int right = nums.size() -1 ;
      //找左端点
      while(left < right)
      {
      int mid = left + (right - left) / 2;
      if(nums[mid] < target) left = mid + 1;
      else right = mid;
      }
      if(nums[left] == target) begin = left;
      else return {-1,-1};
      //找右端点
      left = 0,right = nums.size()-1;
      while(left < right)
      {
      int mid = left + (right - left + 1) / 2;
      if(nums[mid] <= target) left = mid;
      else right = mid - 1;
      }
      return {begin,right};
      }
      };
      int main() {
      // 示例1测试
      vector<int> nums1 = {5,7,7,8,8,10};
        int target1 = 8;
        Solution s;
        vector<int> result1 = s.searchRange(nums1, target1);
          cout << "示例1输出：[" << result1[0] << "," << result1[1] << "]" << endl; // 预期输出[3,4]
          // 示例2测试
          vector<int> nums2 = {5,7,7,8,8,10};
            int target2 = 6;
            vector<int> result2 = s.searchRange(nums2, target2);
              cout << "示例2输出：[" << result2[0] << "," << result2[1] << "]" << endl; // 预期输出[-1,-1]
              // 示例3测试
              vector<int> nums3;
                int target3 = 0;
                vector<int> result3 = s.searchRange(nums3, target3);
                  cout << "示例3输出：[" << result3[0] << "," << result3[1] << "]" << endl; // 预期输出[-1,-1]
                  return 0;
                  }

总结

本文通过两个经典题目讲解了二分查找的基础用法和进阶应用，在实现过程中需要注意边界条件的处理，比如整数溢出、死循环等问题。二分查找的思想不仅适用于简单的元素查找，还能扩展到查找边界、寻找旋转点等场景，掌握好二分查找对算法学习至关重要。希望本文能帮助你更好地理解和运用二分查找算法。

✨ 坚持用清晰易懂的图解 + 代码语言，让每个知识点都简单直观！
个人主页 ：不呆头 · CSDN
代码仓库 ：不呆头 · Gitee
专栏系列：
《C语言》
《数据结构》
《C++》
《Linux》
座右铭 ： “不患无位，患所以立。”

posted @ 2026-01-15 10:53 clnchanpin 阅读(12) 评论(0) 收藏举报

刷新页面返回顶部