【52】均值漂移（MeanShift）算法原理解析与代码构建

简介

本文系统解析均值漂移（MeanShift）算法，从“沿密度上升寻聚类”的核心逻辑切入，推导基础运算公式与核函数改进版，结合聚类、图像分割等典型应用，拆解完整运算步骤，帮助理解其原理与实践价值。

一、均值漂移的核心逻辑：沿着密度梯度寻找聚类中心

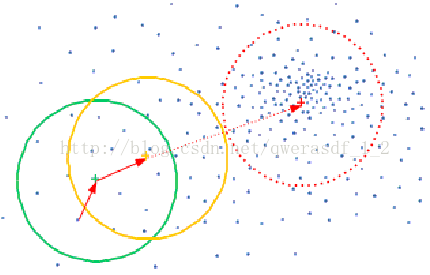
均值漂移的本质是基于密度的无监督聚类算法通过，核心思想能够概括为：让中心点沿着样本密度上升的方向“漂移”，直到停在密度最高点（聚类中心）。

想象在高维特征空间中（比如二维平面的样本点分布），每个点都像“密度磁场”中的粒子——密度越高的区域，对中心点的“吸引力”越强。具体操作逻辑如下：

1. 选一个初始中心点（比如随机选样本点）；
2. 划定带宽为h的高维球区域（二维是圆，高维是超球）；
3. 计算区域内所有点相对于中心点的向量（即$x_i-x$，$x_i$是区域内点，$x$是当前中心）；
4. 求向量的平均值（偏移均值），将中心点移动到这个均值位置；
5. 重复上述步骤，直到中心点移动幅度小于阈值（如$10^{-5}$），此时中心就是密度极点（聚类中心）。
   

二、均值漂移的运算公式：从基础版到核函数改进

2.1 基础版均值漂移公式

基础版对区域内所有点“等权处理”，偏移均值公式为：

$$M(x)=\frac{1}{k}\sum _{x_i\in S_h}(x_i-x)$$

参数说明：

• $S_h$：以$x$为中心、带宽$h$为半径的高维球区域；
• $k$：$S_h$内的样本点数量；
• $x_i$：$S_h$内的样本点；
• $M(x)$：偏移均值（向量平均方向）。

每次迭代后，中心点更新为原中心+偏移均值：$x_{t+1}=x_t+M(x_t)$（$x_t$是第t次迭代的中心）。直到$||M(x_t)||<ϵ$（$ϵ$为收敛阈值），得到聚类中心。

2.2 核函数改进：让近点拥有更高权值

基础版的缺陷是忽略点的距离权重——距离中心越近的点，对密度的贡献应越大。因此引入核函数，给近点分配更高权值。

核函数的作用是距离加权：近点权值高，远点权值低。常用核函数有高斯核、Epanechnikov核等。引入核函数后的偏移均值公式优化为：

$$M_h(x)=\frac{{\sum }_{i=1}^{n}g\left(\frac{\Vert x_i-x{\Vert }^2}{h^2}\right)(x_i-x)}{{\sum }_{i=1}^{n}g\left(\frac{\Vert x_i-x{\Vert }^2}{h^2}\right)}$$

参数说明：

• $n$：带宽$h$内的样本点数量；
• $g(u)$：核函数导数的负值（即$g(u)=-K^{\prime }(u)$，$K(u)$是原始核函数）；
• $\Vert x_i-x\Vert$：$x_i$与$x$的欧氏距离；
• $\frac{\Vert x_i-x{\Vert }^2}{h^2}$：归一化距离（消除带宽影响）。

以高斯核为例：原始核函数$K(u)=e^{-u/2}$，导数$K^{\prime }(u)=-\frac{1}{2}{e}^{-u/2}$，因此$g(u)=\frac{1}{2}{e}^{-u/2}$（通常省略常数，直接用$g(u)=e^{-u/2}$）。此时距离越近，$g(\cdot )$值越大，权值越高，更准确捕捉密度分布。

三、均值漂移的典型应用场景

均值漂移的优势是无需预设聚类数量、能处理非球形簇，广泛应用于以下领域：

3.1 聚类分析

与K-Means不同，均值漂移无需指定“K值”（聚类数量），通过密度自动发现簇。比如“月牙形”“环形”等非球形数据，K-Means失效，均值漂移能准确聚类。

3.2 图像分割

将像素映射到**“颜色+空间位置”特征空间**（如Lab颜色+像素坐标），对特征点聚类——同一簇的像素即为同一语义区域（如前景物体、背景）。常用于前景提取。

3.3 对象轮廓检测

结合“光线传播算法”，均值漂移沿图像边缘的密度梯度移动，勾勒对象轮廓。比如医学图像中分割肿瘤，工业检测中识别零件缺陷。

3.4 目标跟踪

在视频中，通过最大化Bhattacharya系数（衡量目标模板与当前帧的相似性），找到目标新位置。早期经典跟踪算法，优点是速度快、实时性好。

四、均值漂移的完整运算步骤

以聚类任务为例，均值漂移的流程拆解为7步：

1. 初始化中心：从未分类点中随机选初始中心$x_0$。
2. 划定邻域：找到与$x_0$距离$\le h$的点，组成集合$M$（候选簇）。
3. 计算偏移向量：求和$M$中所有点的向量$(x_i-x_0)$，得到总偏移向量。
4. 更新中心：基础版用$x_1=x_0+\frac{1}{|M|}\sum (x_i-x_0)$；核函数版用$x_1=x_0+M_h(x_0)$。
5. 收敛判断：重复2-4，直到中心移动幅度$<ϵ$（如$10^{-5}$），此时中心为聚类中心。
6. 遍历所有点：重复1-5，直到所有点被“访问”（属于至少一个候选簇）。
7. 最终分类：统计每个点被各聚类中心的访问频率，分配给频率最高的中心。

Python代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import MeanShift, estimate_bandwidth
# 生成示例数据
np.random.seed(42)
n_samples = 500
centers = [[1, 1], [-1, -1], [1, -1]]
X, labels_true = make_blobs(n_samples=n_samples, centers=centers, cluster_std=0.5)
# 估计带宽参数
bandwidth = estimate_bandwidth(X, quantile=0.2, n_samples=500)
print(f"Estimated bandwidth: {bandwidth:.3f}")
# 创建MeanShift模型
meanshift = MeanShift(bandwidth=bandwidth, bin_seeding=True)
# 拟合数据
meanshift.fit(X)
# 获取结果
labels = meanshift.labels_
cluster_centers = meanshift.cluster_centers_
# 统计聚类数量
n_clusters = len(np.unique(labels))
print(f"Number of clusters found: {n_clusters}")
# 可视化结果
plt.figure(figsize=(12, 5))
# 原始数据
plt.subplot(1, 2, 1)
plt.scatter(X[:, 0], X[:, 1], c='blue', s=30, alpha=0.5)
plt.title("Original Data")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
# 聚类结果
plt.subplot(1, 2, 2)
colors = ['red', 'green', 'blue', 'cyan', 'magenta', 'yellow', 'black']
for i in range(n_clusters):
# 当前聚类的点
cluster_points = X[labels == i]
plt.scatter(cluster_points[:, 0], cluster_points[:, 1],
c=colors[i % len(colors)], s=30, alpha=0.5,
label=f'Cluster {i}')
# 聚类中心
center = cluster_centers[i]
plt.scatter(center[0], center[1], c='black',
marker='x', s=200, linewidths=3)
plt.title(f"MeanShift Clustering (Clusters: {n_clusters})")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.legend()
plt.tight_layout()
plt.show()
# 输出聚类中心坐标
print("\nCluster Centers:")
for i, center in enumerate(cluster_centers):
print(f"Cluster {i}: [{center[0]:.3f}, {center[1]:.3f}]")
# 统计每个聚类的样本数
unique, counts = np.unique(labels, return_counts=True)
print("\nSamples per cluster:")
for i in range(n_clusters):
print(f"Cluster {i}: {counts[i]} samples")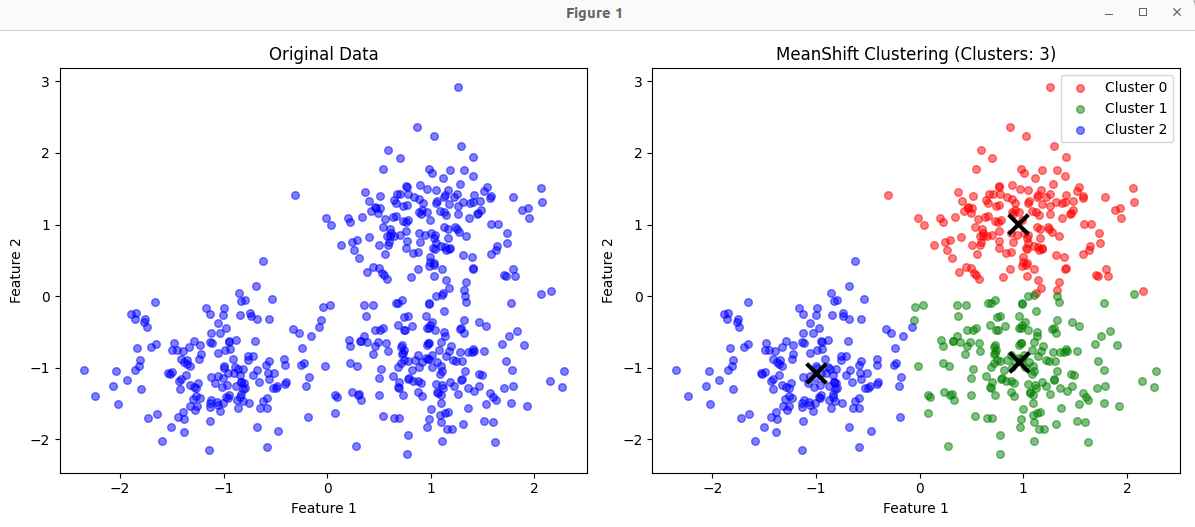

总结

均值漂移是一种直观且强大的密度聚类算法，从“漂移找密度极点”的核心逻辑出发，通过公式推导与核函数改进，应对了等权值的缺陷，广泛应用于聚类、图像分割、目标跟踪等领域。理解其原理与步骤，能更好地将其应用于实际挑战中。

获取更多资料

我给大家整理了一套全网最全的人工智能学习资料（1.5T），包括：机器学习，深度学习，大模型，CV方向，NLP方向，kaggle大赛，实战项目、自动驾驶，AI就业等免费获取。