实用指南:KMP 算法超详细讲解笔记(含全概念 + 全题解题思路)
前言

一、核心概念(必知)
1. 基础字符串概念
| 概念 | 定义 | 示例(字符串 aabaaba,长度 7) |
|---|---|---|
| 字符串 | 字符构成的序列,本文约定下标从 1 开始(输入时前加空格,如 s = ' ' + s) | 处理后:a a b a a b a(下标 1-7) |
| 子串 | 字符串中连续的一段 | 下标 [2,4]:aba |
| 前缀 | 从首端开始到第 i 位结束的子串(区间 [1,i]) | 长度 3 的前缀:aab(下标 [1,3]) |
| 真前缀 | 不包含字符串本身的前缀 | aabaaba 的真前缀:a、aa、aab、aaba、aabaa、aab aab |
| 后缀 | 从第 (n-i+1) 位开始到末端的子串(区间 [n-i+1, n]) | 长度 3 的后缀:baa(下标 [5,7]) |
| 真后缀 | 不包含字符串本身的后缀 | aabaaba 的真后缀:a、ba、aba、aaba、baaba、a baaba |
| 真公共前后缀(border) | 既是字符串的真前缀,又是真后缀的子串 | aabaaba 的 border:a、aaba(共 2 个) |
| π 值(最长 border 长度) | 字符串最长真公共前后缀的长度 | aabaaba 的 π 值 = 4(最长 border 是 aaba) |
2. 关键性质
- 传递性:字符串的 border 的 border 仍是该字符串的 border。例:
aabaaba的 border 是aaba,aaba的 border 是a,则a也是aabaaba的 border。 - 字符串匹配:给定主串 S 和模式串 T,找到 S 中所有与 T 完全相同的子串(又称模式匹配)。例:(S="abcdefcde"),(T="cde"),匹配位置为下标 3-5、7-9。
3. 前缀函数
- 定义:字符串每个前缀子串的 π 值,记为
pi[i],表示长度为 i 的前缀的最长 border 长度。 - 示例(字符串
aabaab,下标 1-6):
| 下标 i | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 前缀子串 | a | aa | aab | aaba | aabaa | aabaab |
pi[i] | 0 | 1 | 0 | 1 | 2 | 3 |
- 小用途:利用 border 传递性,从大到小枚举某个前缀的所有 border。方法:从
pi[i]开始,依次取pi[pi[i]]、pi[pi[pi[i]]]... 直到 0,无遗漏且不重复。
4. 周期与循环节
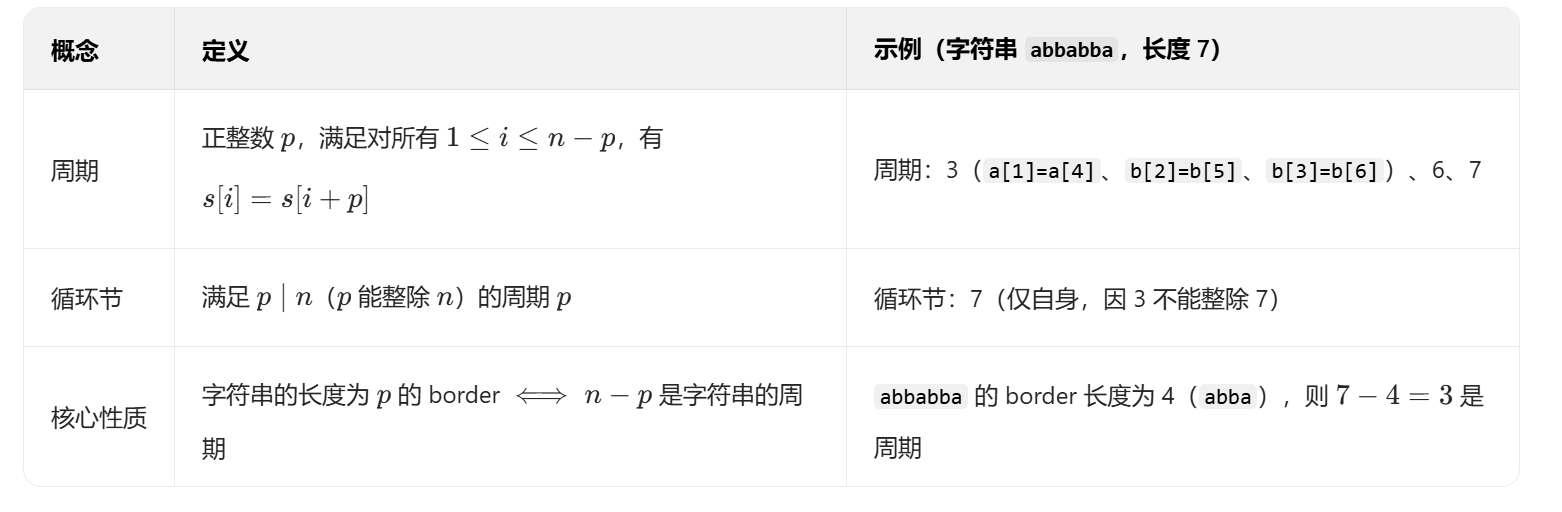
二、前缀函数的计算(核心步骤)
前缀函数是 KMP 算法的基础,计算过程采用动态规划思想,核心是推导状态转移方程。
1. 状态定义
pi[i]:长度为 i 的前缀的最长 border 长度(最长真公共前后缀长度)。
2. 状态转移方程推导
- 核心思路:长度为 i 的前缀的 border,可由长度为 (i-1) 的前缀的 border 推导而来。
- 步骤:
- 设 (j = pi[i-1])(长度为 (i-1) 的最长 border 长度);
- 若 (s[i] == s[j+1]):则
pi[i] = j+1(最长 border 延长 1); - 若不相等:让 (j = pi[j])(回溯到长度为 j 的前缀的最长 border(其也是i-1前缀的次长border)),重复步骤 2,直到 (j=0);
- 若 (j=0) 仍不相等,则
pi[i] = 0。
3. 代码实现(两种写法)
const int N = 2e6 + 10;
string s;
int pi[N];
// 写法1:清晰体现回溯过程
void get_pi() {
cin >> s;
int n = s.size();
s = ' ' + s; // 下标从1开始
for (int i = 2; i <= n; i++) {
int j = pi[i-1]; // 从i-1的最长border开始
while (j && s[i] != s[j+1]) j = pi[j]; // 回溯border
if (s[i] == s[j+1]) j++;
pi[i] = j;
}
}
// 写法2:更简洁,j指针不回退(推荐)
void get_pi_optimized() {
cin >> s;
int n = s.size();
s = ' ' + s;
for (int i = 2, j = 0; i <= n; i++) {
while (j && s[i] != s[j+1]) j = pi[j];
if (s[i] == s[j+1]) j++;
pi[i] = j;
}
}4. 时间复杂度分析
- i 指针每次向后移动 1 位(共 n 次);
- j 指针每次要么向后移动 1 位(最多 n 次),要么向前回溯(总回溯次数不超过 n 次);
- 总时间复杂度:(O(n))(线性时间)。
三、KMP 字符串匹配(前缀函数版)
利用前缀函数实现字符串匹配的核心是拼接字符串,将模式串和主串用特殊字符(如 #)连接,避免模式串内部匹配。
P3375 【模板】KMP - 洛谷
#include
using namespace std;
const int N = 2e6 + 10;
string s, t;
int n, m, pi[N];
int main() {
cin >> s >> t;
n = s.size(), m = t.size();
s = ' ' + t + '#' + s; // 拼接:t+# + s,下标从1开始
for (int i = 2; i <= n + m + 1; i++) {
int j = pi[i-1];
while (j && s[i] != s[j+1]) j = pi[j];
if (s[i] == s[j+1]) j++;
pi[i] = j;
if (j == m) { // 匹配成功
cout << i - 2 * m << endl; // 起始位置
}
}
// 输出s2的每个前缀的最长border长度
for (int i = 1; i <= m; i++) cout << pi[i] << " ";
cout << endl;
return 0;
} 四、next 数组版本(传统 KMP)
大多数教材的 next 数组版本,本质是将 “计算前缀函数” 和 “匹配” 拆分为两步,next 数组等价于前缀函数数组。
1. 实现步骤
- 预处理模式串 t,计算 next 数组(与前缀函数计算逻辑一致);
- 用 next 数组加速主串 s 和模式串 t 的匹配,避免重复比较。
2. 代码实现
const int N = 2e6 + 10;
string s, t;
int n, m, ne[N]; // ne数组即前缀函数数组
void kmp() {
n = s.size(), m = t.size();
s = ' ' + s, t = ' ' + t;
// 步骤1:预处理模式串的next数组
for (int i = 2, j = 0; i <= m; i++) {
while (j && t[i] != t[j+1]) j = ne[j];
if (t[i] == t[j+1]) j++;
ne[i] = j;
}
// 步骤2:利用next数组匹配主串和模式串
for (int i = 1, j = 0; i <= n; i++) {
while (j && s[i] != t[j+1]) j = ne[j]; // 回溯next数组
if (s[i] == t[j+1]) j++;
if (j == m) { // 匹配成功
cout << i - m + 1 << endl; // 起始位置(下标从1开始)
j = ne[j]; // 可选:继续匹配重叠子串
}
}
}3. 与前缀函数版的区别
- 前缀函数版:一次拼接字符串,一次计算前缀函数,代码简洁;
- next 数组版:分两步计算,逻辑更贴近 “暴力匹配优化”,易理解传统 KMP 思想;
- 本质等价:两者时间复杂度均为 (O(n+m)),仅实现形式不同。
五、周期与循环节(拓展应用)
基于前缀函数的周期性质,可解决字符串重复次数、最短循环节等问题。
10035. 「一本通 2.1 练习 1」Power Strings - 题目 - LibreOJ
题目描述
- 给定字符串,求其最多由多少个相同子串重复连接而成(如
ababab输出 3)。
#include
using namespace std;
const int N = 1e6 + 10;
string s;
int n, pi[N];
int kmp() {
n = s.size();
s = ' ' + s;
for (int i = 2; i <= n; i++) {
int j = pi[i-1];
while (j && s[i] != s[j+1]) j = pi[j];
if (s[i] == s[j+1]) j++;
pi[i] = j;
}
int p = n - pi[n];
if (n % p == 0) return n / p;
else return 1;
}
int main() {
while (cin >> s) {
if (s == ".") break;
cout << kmp() << endl;
}
return 0;
} 10045. 「一本通 2.2 练习 1」Radio Transmission - 题目 - LibreOJ
题目描述
- 字符串由某个子串不断自我连接形成,求该子串的最短长度。
#include
using namespace std;
const int N = 1e6 + 10;
string s;
int n, pi[N];
int main() {
cin >> n >> s;
s = ' ' + s;
for (int i = 2; i <= n; i++) {
int j = pi[i-1];
while (j && s[i] != s[j+1]) j = pi[j];
if (s[i] == s[j+1]) j++;
pi[i] = j;
}
cout << n - pi[n] << endl; // 最短循环节长度
return 0;
} 六、练习题详解(含解题思路)
1. 剪花布条(LibreOJ10043)
10043. 「一本通 2.2 例 1」剪花布条 - 题目 - LibreOJ
题目描述
- 给定花布条(主串)和小饰条(模式串),求最多能剪出多少个不重叠的小饰条。
解题思路
- 核心:匹配成功后,跳过模式串长度的位置(避免重叠);
- 实现:拼接模式串 + 特殊字符 + 主串,计算前缀函数;
- 当
pi[i] == m时,计数 + 1,且i += m-1(跳过当前匹配区间)。
int main() {
while (cin >> s >> t) {
if (s == "#") break; // 输入结束条件
n = s.size(), m = t.size();
s = ' ' + t + '#' + s; // 拼接
memset(pi, 0, sizeof pi);
int ret = 0;
for (int i = 2; i <= n + m + 1; i++) {
int j = pi[i-1];
while (j && s[i] != s[j+1]) j = pi[j];
if (s[i] == s[j+1]) j++;
pi[i] = j;
if (j == m) { // 匹配成功
ret++;
i += m - 1; // 跳过m个位置,避免重叠
j = 0; // 重置j,重新匹配
}
}
cout << ret << endl;
}
return 0;
}2. Seek the Name(LibreOJ10036)
10036. 「一本通 2.1 练习 2」Seek the Name, Seek the Fame - 题目 - LibreOJ
题目描述
- 给定字符串,输出所有既是前缀又是后缀的子串长度(递增排序)。
解题思路
- 核心:利用 border 的传递性,从
pi[n]回溯所有 border; - 步骤:
- 计算前缀函数
pi; - 从
pi[n]开始,依次取pi[pi[n]]、pi[pi[pi[n]]]... 直到 0,收集所有非 0 值; - 反转收集到的数组(因回溯是从长到短),最后加上字符串本身长度 n。
- 计算前缀函数
int main() {
while (cin >> s) {
int top = 0;
n = s.size();
s = ' ' + s;
memset(pi, 0, sizeof pi);
for (int i = 2; i <= n; i++) {
int j = pi[i-1];
while (j && s[i] != s[j+1]) j = pi[j];
if (s[i] == s[j+1]) j++;
pi[i] = j;
}
// 收集所有border长度(从长到短)
for (int i = pi[n]; i; i = pi[i]) {
ret[++top] = i;
}
// 反转后输出(递增排序),最后加n
for (int i = top; i >= 1; i--) cout << ret[i] << " ";
cout << n << endl;
}
return 0;
}3. Censoring S(洛谷 P4824)
P4824 [USACO15FEB] Censoring S - 洛谷
题目描述
- 反复删除主串 S 中第一个出现的模式串 T,直到 S 中无 T(删除可能产生新的 T),输出最终 S。
解题思路
- 核心:用栈记录前缀函数的状态,删除匹配部分时回溯栈;
- 步骤:
- 拼接模式串 + 特殊字符 + 主串;
- 栈存储当前位置的下标,栈顶元素对应前一个位置的下标;
- 当
pi[i] == m时,弹出栈中最后 m 个元素(删除匹配部分); - 最终栈中元素对应删除后的字符串下标,输出对应字符。
#include
using namespace std;
const int N = 2e6 + 10;
string s, t;
int n, m, pi[N];
int st[N], top; // 栈:存储当前处理的下标
int main() {
cin >> s >> t;
n = s.size(), m = t.size();
s = ' ' + t + '#' + s; // 拼接
st[++top] = 1; // 初始栈顶为1(t的第一个字符下标)
for (int i = 2; i <= n + m + 1; i++) {
int j = pi[st[top]]; // 从栈顶的前缀函数开始
while (j && s[i] != s[j+1]) j = pi[j];
if (s[i] == s[j+1]) j++;
pi[i] = j;
st[++top] = i; // 入栈
if (j == m) { // 匹配成功,删除m个字符
for (int k = 0; k < m; k++) top--; // 出栈m次
}
}
// 输出删除后的字符串(跳过t+#部分)
for (int i = m + 2; i <= top; i++) cout << s[st[i]];
cout << endl;
return 0;
} 4. ABB(洛谷 P9606)
题目描述
- 给定字符串,求在末尾添加最少字符使其成为回文串。
解题思路
- 核心:找到字符串的最长回文后缀,添加的字符数 = 总长度 - 最长回文后缀长度;
- 如何找最长回文后缀?
- 设 t 为 s 的逆序字符串;
- 构造新串 (t + '#' + s),其最长 border 长度即为 s 的最长回文后缀长度(因回文后缀逆序后是前缀)。
#include
#include
using namespace std;
const int N = 8e5 + 10;
string s, t;
int n, pi[N];
int main() {
cin >> n >> s;
t = s;
reverse(t.begin(), t.end()); // 逆序s得到t
s = ' ' + t + '#' + s; // 构造新串
for (int i = 2; i <= n + n + 1; i++) {
int j = pi[i-1];
while (j && s[i] != s[j+1]) j = pi[j];
if (s[i] == s[j+1]) j++;
pi[i] = j;
}
// 最少添加字符数 = n - 最长回文后缀长度
cout << n - pi[n + n + 1] << endl;
return 0;
} 


 浙公网安备 33010602011771号
浙公网安备 33010602011771号