YOLOv8【第七章：损失函数篇·第6节】一文搞定，InnerShapeIoU内部形状损失！ - 指南

本文收录于《YOLOv8实战：从入门到深度优化》专栏。该专栏系统复现并梳理全网各类YOLOv8 改进与实战案例（当前已覆盖分类 / 检测 / 分割 / 追踪 / 关键点 / OBB 检测等方向），坚持持续更新 + 深度解析，质量分长期稳定在 97 分以上，可视为当前市面上覆盖较全、更新较快、实战导向极强的 YOLO 改进系列内容之一。
部分章节也会结合国内外前沿论文与 AIGC 等大模型技术，对主流改进方案进行重构与再设计，内容更偏实战与可落地，适合有工程需求的同学深入学习与对标优化。

✨ 特惠福利：当前限时活动一折秒杀，一次订阅，终身有效，后续所有更新章节全部免费解锁，点此查看详情

全文目录：

• • 上期回顾
  • 1. 引言：Bbox回归的“天花板”——甜甜圈问题 (The Donut Problem)
  • • 1.1 场景复现：完美的回归，错误的结果 (Mermaid图解)
    • 1.2 “框”与“物”的分离：Bbox的局限性
    • 1.3 什么是“实例感知”回归？
  • 2. 为什么必须感知“内部形状”？
  • • 2.1 Case 1: L形/细长物体（如：L形沙发、电线杆）
    • 2.2 Case 2: 拓扑结构差异（如：字母'O' vs 'C'）
    • 2.3 Case 3: 辅助高质量实例分割
  • 3. InnerShapeIoU的哲学：从“框”到“内容”
  • • 3.1 核心思想：$L_{Total}=L_{Bbox}+\lambda \cdot L_{InnerShape}$
    • 3.2 $L_{InnerShape}$的“锚点”：内部关键点（Keypoints）
  • 4. 核心机制：基于Keypoints的$L_{InnerShape}$
  • • 4.1 引入新监督：关键点相对坐标
    • 4.2 模型改造：从$(x,y,w,h)$ 到 $(x,y,w,h,k_1,...,k_N)$
    • 4.3 $L_{InnerShape}$的梯度：反向传播的“魔法”
    • 4.4 几何图解：$w,h$误差如何扭曲内部结构
  • 5. 深度分析：$L_{InnerShape}$ vs $L_{CIoU}/L_{EIoU}$
  • • 5.1 “盲目”的$L_{asp}$vs “有据”的$L_{InnerShape}$
    • 5.2 解决“L形”物体的Bbox歧义性
    • 5.3 $L_{InnerShape}$：一种“内容感知”的耦合惩罚
  • 6. 局限性与“鸡生蛋”问题
  • • 6.1 依赖昂贵的“额外标注”（Keypoints）
    • 6.2 “鸡生蛋”：Bbox不准$⟹$Keypoints不准
    • 6.3 解决方案：Focal-InnerShape ($Io{U}^{\gamma }\cdot L_{InnerShape}$ )
  • 7. Python代码实战 (概念)：达成 `InnerShapeLoss`
  • • 7.1 重新定义模型输出
    • 7.2 `InnerShapeLoss` 模块化实现
    • 7.3 代码解析
  • 8. 总结：Bbox回归的“内容感知”革命
  • 9. 下期预告：QFL质量Focal Loss与IoU感知
  • 文末福利，等你来拿！
  • Who am I?

上期回顾

大家好！欢迎回到《YOLOv8专栏》！在上一篇《YOLOv8【第七章：损失函数篇·第5节】一文搞定，ShapeIoU形状感知损失函数！》内容中，我们进行了一次深刻的“形状”哲学思辨：

1. 几何特征提取：大家没有沿用$w,h$这两个“间接”属性，而是回归到Bbox最基础的“几何特征”——4个角点。

2. “耦合”损失推导：通过计算“中心化”Bbox的4个角点对应距离，我们惊奇地发现$d_1=d_2=d_3=d_4$。这推导出 $L_{Shape}$ 的本质是 $(\Delta w,\Delta h)$ 误差向量的 $L_2$范数：
   $$L_{Shape}\propto ||(\Delta w,\Delta h)|{|}_2$$

3. 两大策略对比：大家通过关键场景测试，清晰地对比了两种形状损失策略：

   • $L_{EIoU}$(解耦 / 各向异性):$L_{asp}=(\frac{\Delta w}{C_w}{)}^2+(\frac{\Delta h}{C_h}{)}^2$。它对闭包框$C$的“短边”方向上的误差（如$C_h=10$）惩罚极其严重。
   • $L_{ShapeIoU}$(耦合 / 各向同性):$L_{asp}=\frac{||(\Delta w,\Delta h)|{|}_2}{||(C_w,C_h)|{|}_2}$。它只关心 $(\Delta w,\Delta h)$误差向量的“总长度”（$L_2$距离），而不在乎其方向。

上期的探索让我们意识到，$L_{Shape}$ 的设计远非 $L_{EIoU}$一种方案，ShapeIoU的“耦合”思想为我们提供了全新的视角。

然而，无论是$L_{EIoU}$ 还是 $L_{ShapeIoU}$，它们都只是在“拟合”$B_{gt}$ 的 $w_{gt}$ 和 $h_{gt}$。它们都默认$B_{gt}$这个“矩形”就是我们的终极目标。

可 $B_{gt}$只是一个“标签框”，它不是“物体”本身！这种“指框为物”的回归方式，已经触碰到了Bbox回归的“天花板”。

1. 引言：Bbox回归的“天花板”——甜甜圈问题 (The Donut Problem)

我们所有的IoU Loss（CIoU, EIoU,$\alpha$-IoU…）都在追求一个目标：$IoU\to 1$，即 $L_{IoU}\to 0$。

但当 $L_{IoU}=0$时，我们就真的“赢”了吗？

1.1 场景复现：完美的回归，错误的结果 (Mermaid图解)

场景：检测一个“甜甜圈” (或字母 ‘O’)。就是我们的目标

• $B_{gt}$(真实框)：是一个紧密包裹住“甜甜圈”的实心正方形。
• $M_{gt}$(真实物体)： 是一个空心的环形。
• $B_{pred}$(预测框)：经过模型训练，$B_{pred}$ 与 $B_{gt}$ 完美重合。

此时的损失：

• $L_{IoU}=1-1=0$
• $L_{DIoU}=0$(中心点重合)
• $L_{CIoU}=0$(长宽比一致)

结论：模型的Bbox损失为 0！这是一个“完美”的预测。

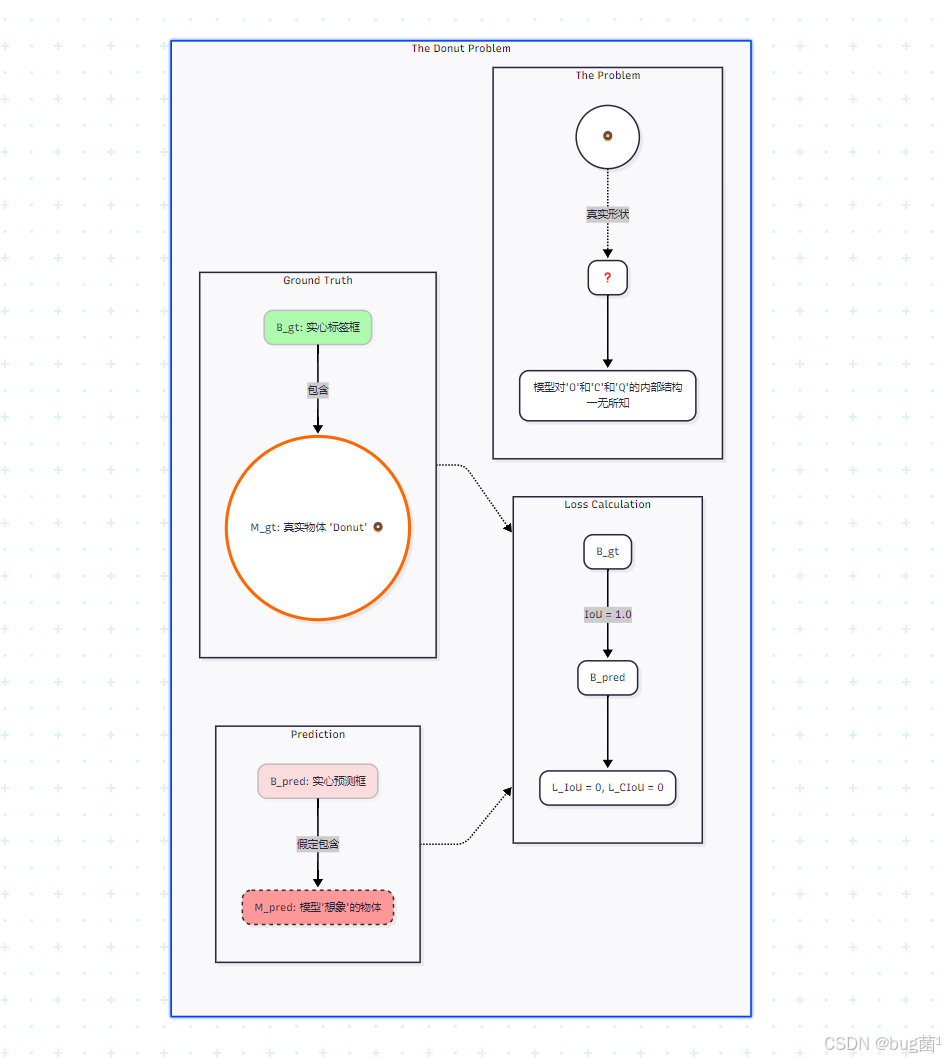
图解分析：
所有的Bbox损失函数，都只在$B_{gt}$ 和 $B_{pred}$ (两个实心矩形) 之间进行比较。它们完美重合了，损失为0。
但 $B_{pred}$(实心) 和$M_{gt}$(空心) 在拓扑结构上是根本不同的！模型从 $L_{IoU}=0$中学不到任何关于“空心”这个“内部形状”的信息。

1.2 “框”与“物”的分离：Bbox的局限性

“甜甜圈问题”暴露了Bbox回归的根本局限性：
在拟合“物”（Content）。就是Bbox回归，是在拟合“框”（Container），而不

$B_{gt}$ 只是 $M_{gt}$的一个极其粗糙、轴对齐的外壳。
我们之前所有的$L_{Shape}$(CIoU, EIoU, ShapeIoU) 都在拼命地拟合这个外壳的 $w_{gt},h_{gt}$，而这个 $w_{gt},h_{gt}$本身就丢失了物体99%的内部形状信息。

“实例感知”回归？就是1.3 什么

“实例感知”（Instance-aware）回归，是一种更高级的回归。它不仅要知道物体在哪里（Bbox），还要在一定程度上理解它是什么形态（Shape）。

大家需要的损失函数，必须能“穿透”$B_{gt}$的外壳，去“采样”$M_{gt}$内部的结构信息，并以此来指导$B_{pred}$ 的回归。
这就是 $L_{InnerShape}$ 的使命。

2. 为什么需感知“内部形状”？

2.1 Case 1: L形/细长物体（如：L形沙发、电线杆）

• 问题：对于一个’L’形的沙发，$B_{gt}$会框出一个大正方形，这个正方形的右上角 1/4 区域完全是空的。
• Bbox歧义性： 存在多种 $w,h$组合，它们都能以高$IoU$“框住”这个L形。
• $L_{EIoU}$ 的困境：$L_{EIoU}$ 会试图让 $B_{pred}$ 的 $w,h$ 匹配 $B_{gt}$ 的 $w_{gt},h_{gt}$。但 $B_{gt}$本身就是一个“臃肿”且“充满歧义”的框。
• $L_{InnerShape}$ 的优势： 如果 $L_{InnerShape}$能感知到’L’形的几个“拐点”，它就能提供一个“收缩”的梯度，迫使$B_{pred}$ 的 $w,h$盲目匹配那个“臃肿”的就是变得更“紧凑”，而不$B_{gt}$。

2.2 Case 2: 拓扑结构差异（如：字母’O’ vs ‘C’）

• 问题：字母’O’和字母’C’的$B_{gt}$ 可能是完全相同的。
• Bbox的无能：任何Bbox Loss都无法区分这两种情况。
• $L_{InnerShape}$ 的优势：'O’的内部关键点是“闭合”的，'C’的内部关键点是“开放”的。$L_{InnerShape}$ 可以惩罚 $B_{pred}$对此种内部拓扑结构的错误建模，从而供应Bbox Loss无法提供的、更高级的“形状”梯度。

2.3 Case 3: 辅助高质量实例分割

• 问题：在实例分割任务中（如YOLOv8-seg），模型需要先预测Bbox，再在该Bbox内预测Mask。
• Bbox的基石作用： 如果 $B_{pred}$本身就是“臃肿”的（比如’L’形物体的Bbox），那么分割头（Mask Head）就需费力地去“擦除”Bbox中多余的空白区域。
• $L_{InnerShape}$ 优势： 如果 $L_{Bbox}$(Bbox损失) 已经包括了$L_{InnerShape}$，那么它会“逼迫”Bbox Head去预测一个更“紧凑”、更“贴合”物体真实轮廓的$B_{pred}$。这个高质量的$B_{pred}$将极大地降低分割头的学习难度。

3. InnerShapeIoU的哲学：从“框”到“内容”

3.1 核心思想：$L_{Total}=L_{Bbox}+\lambda \cdot L_{InnerShape}$

$L_{InnerShape}$一个就是(内部形状损失) 必须附加项。我们不能抛弃$L_{Bbox}$ (如 $L_{CIoU}$ 或 $L_{EIoU}$)，因为 $L_{Bbox}$负责核心的“定位”（Localization）和“尺度”（Scale）回归。

大家的新损失函数将是：

$$L_{Total}=L_{Bbox\_Regression}+\lambda \cdot L_{InnerShape\_Regression}$$

其中 $\lambda$是一个平衡权重。

3.2 $L_{InnerShape}$的“锚点”：内部关键点（Keypoints）

如何建模“内部形状”？

• 方案A (Mask-based)：通过如引言中提到的，我们能够用$B_{pred}$ 和 $B_{gt}$ 裁剪 $M_{pred}$ 和 $M_{gt}$，然后计算 Mask IoU。这是可行的，但它应该一个分割头来预测 $M_{pred}$。这已经超出了“Bbox回归”的范畴，进入了“分割”的领域。
• 方案B (Keypoint-based)：这是一个更“轻量级”且更巧妙的方案。我们不需要完整的Mask，只需要物体内部的$N$ 个 “语义关键点”（Semantic Keypoints）或“结构骨架点”（Skeleton Points）。

例如，对于“人”，我们可以使用 COCO-Pose 的17个关键点（眼、鼻、肩、肘…）。
对于“甜甜圈”，我们允许应用其内环和外环上的8个点。

$L_{InnerShape}$的本质，就是$B_{pred}$的“内部”与$B_{gt}$的“内部结构”之间的匹配损失。

4. 核心机制：基于Keypoints的$L_{InnerShape}$

这是 $InnerShapeIoU$概念的核心。

4.1 引入新监督：关键点相对坐标

我们要求新的Ground Truth：

对于 $B_{gt}=(x_{c_{g}t},y_{c_{g}t},w_{gt},h_{gt})$，大家还得一组$N$ 个关键点 $K_{gt}=\{k_1^{gt},...,k_N^{gt}\}$。

$k_i^{gt}=(x_i^{gt},y_i^{gt})$(绝对坐标)。

为了让 $L_{InnerShape}$成为一个“形状”损失（位置无关），大家将其转换为相对于 $B_{gt}$中心点和尺度的“归一化”坐标：

$$k_{i\_norm}^{gt}=(\frac{x_i^{gt}-x_{c\_gt}}{w_{gt}},\frac{y_i^{gt}-y_{c\_gt}}{h_{gt}})$$

$k_{i\_norm}^{gt}$的值域通常在$[-0.5,0.5]$ 之间。
这组 $K_{norm}^{gt}=\{k_{1\_norm}^{gt},...,k_{N\_norm}^{gt}\}$，就是 $B_{gt}$的“内部结构”的数学描述！

4.2 模型改造：从$(x,y,w,h)$ 到 $(x,y,w,h,k_1,...,k_N)$

我们必须改造YOLOv8的检测头（Detection Head）。
原始Head对每个Bbox预测：

• 4 个值 (Bbox)
• $C$个值 (Classes)

新Head（InnerShape Head）需要预测：

• 4 个值 (Bbox:$x_c,y_c,w,h$)
• $C$个值 (Classes)
• $N\times 2$个值 (Keypoints:$k_{1\_norm}^{pred},...,k_{N\_norm}^{pred}$)

模型预测的也是归一化的关键点偏移量。

4.3 $L_{InnerShape}$的梯度：反向传播的“魔法”

现在，激动人心的时刻到了。我们如何计算$L_{InnerShape}$ 并让它反向传播以优化 $w,h$？

1. 从输出中提取：

   • $B_{pred}=(x_c,y_c,w,h)$
   • $K_{norm}^{pred}=\{(\Delta x_1^{pred},\Delta y_1^{pred}),...\}$

2. 从Ground Truth中提取：

   • $B_{gt}=(x_{c\_gt},y_{c\_gt},w_{gt},h_{gt})$
   • $K_{norm}^{gt}=\{(\Delta x_1^{gt},\Delta y_1^{gt}),...\}$

3. 计算“预测的绝对关键点”$K_{abs}^{pred}$：

   • $x_i^{pred}=x_c+\Delta x_i^{pred}\cdot w$
   • $y_i^{pred}=y_c+\Delta y_i^{pred}\cdot h$

4. 计算“真实的绝对关键点”$K_{abs}^{gt}$：

   • (注：我们不需要$B_{gt}$来计算，GT$K_{abs}^{gt}=(x_i^{gt},y_i^{gt})$是直接给定的)

5. 计算 $L_{InnerShape}$：

   • 通常使用 L1, L2 或 OKS (Object Keypoint Similarity) 损失。
   • $L_{InnerShape}={\sum }_{i=1}^N\text{L1}((x_i^{pred},y_i^{pred}),(x_i^{gt},y_i^{gt}))$
   • $L_{InnerShape}={\sum }_{i=1}^N|(x_c+\Delta x_i^{pred}\cdot w)-x_i^{gt}|+|(y_c+\Delta y_i^{pred}\cdot h)-y_i^{gt}|$

梯度的产生：
我们来看 $L_{InnerShape}$ 对 $w$ 和 $h$ 的偏导数：

$$\frac{\partial L_{InnerShape}}{\partial w}=\sum _{i=1}^N\text{sign}((x_c+\Delta x_i^{pred}\cdot w)-x_i^{gt})\cdot \Delta x_i^{pred}$$

$$\frac{\partial L_{InnerShape}}{\partial h}=\sum _{i=1}^N\text{sign}((y_c+\Delta y_i^{pred}\cdot h)-y_i^{gt})\cdot \Delta y_i^{pred}$$

这就是魔法！ ‍♂️

• $L_{InnerShape}$ 对 $w$产生了梯度！
• $L_{InnerShape}$ 对 $h$ 产生了梯度

$L_{Bbox}$ (如 $L_{EIoU}$) 也在对 $w,h$ 产生梯度。

现在， $w,h$的总梯度是：

$$\frac{\partial L_{Total}}{\partial w}=\frac{\partial L_{Bbox}}{\partial w}+\lambda \cdot \frac{\partial L_{InnerShape}}{\partial w}$$

4.4 几何图解：$w,h$误差如何扭曲内部结构

场景： 真实物体 $M_{gt}$是一个瘦高的人 ️ ($w_{gt}=10,h_{gt}=40$)。

• $B_{gt}$(实线绿框) 完美包裹。
• $K_{gt}$(绿色圆点) 是其肩部和臀部的4个关键点。

预测： 模型预测 $B_{pred}$(虚线红框)$IoU=1$，但 $w,h$ 搞反了 ($w=40,h=10$)。

• 模型 同时预测了正确的归一化 关键点 $K_{norm}^{pred}=K_{norm}^{gt}$。

计算 $K_{abs}^{pred}$(红色X点)：

$B_{pred}$ 用 $w=40$(一个大宽度) 和$h=10$(一个小高度) 去“拉伸”这些归一化坐标。
结果：预测出的绝对关键点$K_{abs}^{pred}$(红色X) 被“压扁”了！

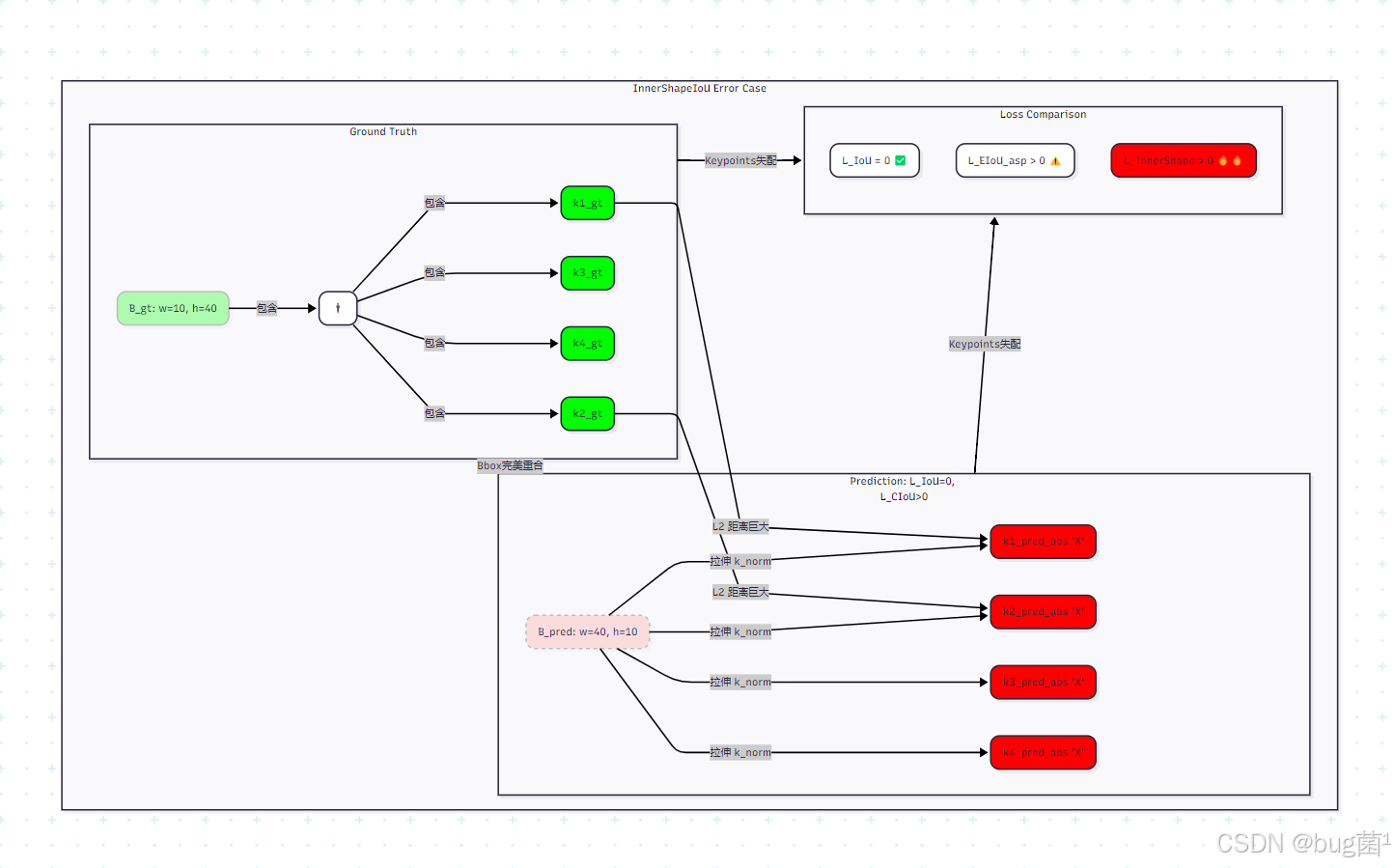
图解分析：

1. $B_{pred}$ 和 $B_{gt}$完美重合（只是为了说明），$L_{IoU}=0$。

2. $L_{EIoU}$会惩罚这个，因为$(\frac{40-10}{C_w}{)}^2+(\frac{10-40}{C_h}{)}^2>0$。

3. $L_{InnerShape}$也会惩罚这个！ 因为 $B_{pred}$ 的 $w=40,h=10$(错误) 应用到$K_{norm}^{pred}$(正确) 上，得到了$K_{abs}^{pred}$(红色X点，被压扁)，$K_{abs}^{pred}$ 与 $K_{abs}^{gt}$(绿色圆点) 之间产生了巨大的$L2$ 距离。

4. 这个 $L_{InnerShape}$ 损失会产生 $\frac{\partial L}{\partial w}$ 和 $\frac{\partial L}{\partial h}$梯度，“告诉”模型：

   • “你的 $w=40$太大了，它把内部结构拉得太宽了，快减小$w$！”
   • “你的 $h=10$太小了，它把内部结构压得太扁了，快增大$h$！”

5. 深度分析：$L_{InnerShape}$ vs $L_{CIoU}/L_{EIoU}$

5.1 “盲目”的$L_{asp}$vs “有据”的$L_{InnerShape}$

• $L_{EIoU}$ (盲目):

  • $L_{EIoU}$ 的 $L_{asp}=(\frac{w-w_{gt}}{C_w}{)}^2+...$是“盲目”的。它只知道 $B_{gt}$ 的 $w_{gt},h_{gt}$是“真理”，它不理解为什么。
  • 它惩罚 $\Delta w,\Delta h$是因为它*“和$B_{gt}$不一样”*。

• $L_{InnerShape}$ (有据):

  • $L_{InnerShape}$是“有理有据”的。
  • 它惩罚 $\Delta w,\Delta h$是因为它*“扭曲了物体的内部结构”*。

$L_{InnerShape}$是一种更高级、更符合物理直觉、基于“内容感知”（Content-Aware）的形状损失。

5.2 解决“L形”物体的Bbox歧义性

• $L_{EIoU}$ 的困境：对于’L’形物体，$B_{gt}$是一个“臃肿”的大方块。$L_{EIoU}$会“错误地”奖励$B_{pred}$去匹配该“臃肿”的$B_{gt}$。

• $L_{InnerShape}$ 的胜利：'L’形物体的关键点$K_{gt}$ 只分布在 $B_{gt}$的左侧和下侧。

  • 如果 $B_{pred}$ 也变得和 $B_{gt}$一样“臃肿”，它（为了最小化$L_{InnerShape}$）会被迫学习到 $K_{norm}^{pred}$也只分布在左下角。
  • 这会鼓励 $B_{pred}$ 的 $w,h$收缩，以更紧密地包裹$K_{abs}^{pred}$。
  • $L_{InnerShape}$ 提供了 $L_{Bbox}$无法提供的“收缩”梯度，奖励更“紧凑”（Tighter）的Bbox。

5.3 $L_{InnerShape}$：一种“内容感知”的耦合惩罚

在第5节中，我们讨论了$L_{EIoU}$（解耦）和 $L_{ShapeIoU}$（耦合）的区别。

$L_{ShapeIoU}=\frac{||(\Delta w,\Delta h)|{|}_2}{c}$是一种“盲目”的耦合。

$L_{InnerShape}$ 是一种“内容感知”的“耦合”。

$L_{InnerShape}$ 对 $w$ 和 $h$的梯度，取决于所有$N$ 个关键点的归一化坐标$(\Delta x_i^{pred},\Delta y_i^{pred})$。

$w,h$的优化被物体内部$N$ 个点的几何分布（即“形状”）牢牢地“耦合”在了一起。

$L_{InnerShape}$才是大家追求的、真正意义上的“形状”损失！

6. 局限性与“鸡生蛋”问题

6.1 依赖昂贵的“额外标注”（Keypoints）

这是 $L_{InnerShape}$最大的软肋。

标准的COCO数据集只有Bbox和Mask。只有COCO-Pose子集才有人体17个关键点。

对于“汽车”、“甜甜圈”等物体，我们根本没有现成的关键点标注。

这意味着 $L_{InnerShape}$无法“开箱即用”，它需耗费巨资去获取“内部结构”的额外标注。

6.2 “鸡生蛋”：Bbox不准$⟹$Keypoints不准

$L_{InnerShape}$的计算依赖于$B_{pred}=(x_c,y_c,w,h)$。

$$L_{InnerShape}=\sum |(x_c+\Delta x_i^{pred}\cdot w)-x_i^{gt}|+...$$

在训练早期：

$B_{pred}$ 的 $x_c,y_c$可能偏了十万八千里。

此时，$L_{InnerShape}$ 的值会极其巨大，它包含 $L_{Dis}$(Bbox中心点) 和$L_{Shape}$ (Bbox $w,h$) 和 $L_{Kpt}$(kpt偏移) 三重误差。

该巨大的、不稳定的$L_{InnerShape}$梯度，可能会干扰$L_{Bbox}$ (如 $L_{CIoU}$) 的稳定收敛。

6.3 解决方案：Focal-InnerShape ($Io{U}^{\gamma }\cdot L_{InnerShape}$ )

我们从第2节 (EIoU) 和第3节 ($\alpha$-IoU) 学到的“聚焦高IoU样本”的策略，在这里至关重要！

我们应该只在$B_{pred}$已经“靠谱”（$IoU$较高）时，才激活$L_{InnerShape}$。

$$L_{Total}=L_{Bbox}+\lambda \cdot (Io{U}^{\gamma })\cdot L_{InnerShape}$$

(其中 $\gamma >0$, $IoU$ 是 $B_{pred}$ 和 $B_{gt}$ 的 $IoU$)

• 当 $IoU\to 0$(早期/离群值):$Io{U}^{\gamma }\to 0$。$L_{Total}\approx L_{Bbox}$。

  • 此时，模型只学习 $L_{Bbox}$（如CIoU），专注于“定位”。

• 当 $IoU\to 1$(后期/可靠样本):$Io{U}^{\gamma }\to 1$。$L_{Total}\approx L_{Bbox}+\lambda \cdot L_{InnerShape}$。

  • 此时，Bbox已经对齐，$L_{Bbox}$ 梯度减小。
  • 模型开始激活$L_{InnerShape}$，专注于“精调”$w,h$以匹配内部结构。

这才是 $L_{InnerShape}$最鲁棒、最合理的打开方式！

7. Python代码实战 (概念)：实现 InnerShapeLoss

$L_{InnerShape}$ 不能集成到 bbox_iou_family 中，因为它需要完全不同的输入（Keypoints）。
我们必须定义一个全新的、模块化的损失类。

7.1 重新定义模型输出

• preds (模型输出): 形状 (B, N_Anchors, 4 + C + N_Kpts*2)
• targets (标签): 形状 (N_gt, 6 + N_Kpts*2) ($batc{h}_{i}dx,cl{s}_{i}d,cx,cy,w,h,kx1,ky1,kx2,ky2,...$) (绝对坐标)

7.2 InnerShapeLoss 模块化实现

import torch
import torch.nn as nn
# 假设我们已经有了 L_CIoU (来自第126篇)
# from .iou_losses import bbox_iou_family
# (这里为了独立运行, 我们假设 L_Bbox 也是L1)
# 实际中, L_Bbox 应该是 CIoU / EIoU
class InnerShapeLoss(nn.Module):
"""
一个概念性的 InnerShapeIoU 损失 (基于Keypoints)
L_Total = L_Bbox + lambda * L_InnerShape
输入 (preds, targets) 必须经过匹配 (e.g., TAL)
preds: (N_matched, 4 + N_Kpts*2)
(cx, cy, w, h, k_norm_x1, k_norm_y1, ...)
targets: (N_matched, 4 + N_Kpts*2)
(cx_gt, cy_gt, w_gt, h_gt, k_abs_x1_gt, k_abs_y1_gt, ...)
"""
def __init__(self, n_kpts=3, lambda_inner=0.5, use_focal_weight=True, gamma=0.5):
super().__init__()
self.n_kpts = n_kpts # 内部关键点数量
self.lambda_inner = lambda_inner # L_InnerShape 的权重
self.l1_loss = nn.L1Loss(reduction='none')
self.use_focal_weight = use_focal_weight # 是否使用 IoU^gamma 抑制
self.gamma = gamma
def forward(self, preds, targets, ious_pred_gt):
"""
preds: (N, 4 + K*2) (归一化kpt)
targets: (N, 4 + K*2) (绝对kpt)
ious_pred_gt: (N,) IoU(B_pred, B_gt)
"""
# --- 1. 提取 Bbox 和 Keypoints ---
# Bbox 预测 (cx, cy, w, h)
bbox_pred = preds[:, :4]
# Bbox 标签 (cx, cy, w, h)
bbox_gt = targets[:, :4]
# Keypoints 预测 (归一化, [-0.5, 0.5])
# (N, K*2) -> (N, K, 2)
kpts_norm_pred = preds[:, 4:].view(-1, self.n_kpts, 2)
# Keypoints 标签 (绝对坐标)
# (N, K*2) -> (N, K, 2)
kpts_abs_gt = targets[:, 4:].view(-1, self.n_kpts, 2)
# --- 2. 计算 L_Bbox (例如: L1 Loss, 实际应为 CIoU/EIoU) ---
# (为了简化, 我们用 L1。在YOLOv8中, 这里会调用 CIoU/EIoU)
L_bbox = self.l1_loss(bbox_pred, bbox_gt).sum(dim=1) # (N,)
# --- 3. ( 核心) 计算 L_InnerShape ---
# 3.1 提取 w, h (N, 1)
w_pred = bbox_pred[:, 2].unsqueeze(-1)
h_pred = bbox_pred[:, 3].unsqueeze(-1)
# 提取 cx, cy (N, 1)
cx_pred = bbox_pred[:, 0].unsqueeze(-1)
cy_pred = bbox_pred[:, 1].unsqueeze(-1)
# 3.2 计算 预测的绝对关键点 K_abs_pred
# k_abs_x = cx + k_norm_x * w
# k_abs_y = cy + k_norm_y * h
# kpts_norm_pred (N, K, 2)
k_norm_x_pred = kpts_norm_pred[..., 0] # (N, K)
k_norm_y_pred = kpts_norm_pred[..., 1] # (N, K)
# (N, 1) + (N, K) * (N, 1) -> (N, K) (广播机制)
k_abs_x_pred = cx_pred + k_norm_x_pred * w_pred
k_abs_y_pred = cy_pred + k_norm_y_pred * h_pred
# (N, K, 2)
k_abs_pred = torch.stack([k_abs_x_pred, k_abs_y_pred], dim=-1)
# 3.3 计算 L_InnerShape (L1 损失)
# (N, K, 2) vs (N, K, 2)
L_inner_kpts = self.l1_loss(k_abs_pred, k_abs_gt) # (N, K, 2)
# (N,)
L_inner_shape = L_inner_kpts.sum(dim=[1, 2]) # 对 K 和 2 (xy) 求和
# --- 4. ( 核心) 动态加权 ---
focal_weight = 1.0 # 默认权重
if self.use_focal_weight:
# (N,) -> (N,)
# .detach() 阻止 IoU 的梯度回传到 focal_weight
focal_weight = (ious_pred_gt.detach() ** self.gamma)
# --- 5. 计算总损失 ---
# (N,) + (N,) * (N,)
L_total = L_bbox + self.lambda_inner * focal_weight * L_inner_shape
# (返回平均损失)
return L_total.mean()

7.3 代码解析

1. 输入：InnerShapeLoss 的 forward 函数需要 preds, targets 和它们之间的 ious。

2. 提取： 我们从 preds 中分离出 $B_{pred}$ 和 $K_{norm}^{pred}$；从 targets 中分离出 $B_{gt}$ 和 $K_{abs}^{gt}$。

3. $L_{Bbox}$： 照常计算 $B_{pred}$ 和 $B_{gt}$之间的Bbox损失（代码中用L1简化，实际应为CIoU）。

4. 核心计算(2)：

   • $k\_abs\_x\_pred=cx\_pred+k\_norm\_x\_pred\ast w\_pred$
   • $k\_abs\_y\_pred=cy\_pred+k\_norm\_y\_pred\ast h\_pred$
   • 这是“魔法”发生的地方。$w,h,cx,cy$（Bbox的预测）被用来“重建”绝对关键点$K_{abs}^{pred}$。

5. $L_{InnerShape}$(3.3)： 我们计算 $K_{abs}^{pred}$ 和 $K_{abs}^{gt}$之间的L1距离。

6. 动态加权(4)：如果启用，我们计算$focal\_weight=Io{U}^{\gamma }$。

7. 总损失(5)：$L_{Total}=L_{Bbox}+\lambda \cdot (focal\_weight)\cdot L_{InnerShape}$。

8. 反向传播： 当 .backward() 被调用时，$L_{InnerShape}$ 的梯度会同时流向 $K_{norm}^{pred}$(优化关键点预测) 和$B_{pred}$(优化Bbox$cx,cy,w,h$以减少结构扭曲)。

8. 总结：Bbox回归的“内容感知”革命

本篇，我们进行了一次“越狱”！我们终于打破了Bbox回归只在“框”上做文章的“天花板”。

1. 甜甜圈问题：我们揭示了Bbox回归的根本局限——拟合“框”（Container）而非“物”（Content）。$L_{IoU}=0$不等于“完美”预测。

2. $L_{InnerShape}$ 哲学：我们必须引入“额外监督”（如关键点）来感知物体“内部结构”，即$L_{Total}=L_{Bbox}+\lambda \cdot L_{InnerShape}$。

3. 核心机制 (Keypoints)：

   • 模型不仅预测Bbox$(x,y,w,h)$，还预测归一化的关键点 $K_{norm}^{pred}$。
   • $L_{InnerShape}$(kpt损失) 是通过$B_{pred}$ (特别是 $w,h$) 重建的 $K_{abs}^{pred}$ 和 $K_{abs}^{gt}$之间的L2/L1损失。

4. “内容感知”的梯度：

   • $L_{InnerShape}$ 为 $w,h$ 提供了全新的、基于“内部结构一致性”的梯度。
   • 它惩罚 $w,h$不再是“盲目”地（基于$w\ne w_{gt}$“有理有据”地（缘于就是），而$w$ 扭曲了 $K_{norm}^{pred}$）。

5. 局限与未来：$L_{InnerShape}$依赖昂贵的“关键点”标注，且在训练早期（$IoU\to 0$）时可能不稳定。$L_{Total}=L_{Bbox}+\lambda \cdot (Io{U}^{\gamma })\cdot L_{InnerShape}$是其最终的、最鲁棒的形态。

$InnerShapeIoU$是一种“实例感知”的Bbox损失，它强迫模型去理解物体的内部几何结构，而不只是画一个“外壳”。

9. 下期预告：QFL质量Focal Loss与IoU感知

到目前为止，大家已经把Bbox回归损失$L_{Reg}$ (即 $L_{Bbox}+L_{InnerShape}$) 挖掘到了极致。

我们所有的Bbox损失 (CIoU, EIoU,$\alpha$-IoU, SIoU…) 都在做一件事：让 $B_{pred}$ 逼近 $B_{gt}$。

与此同时，在另一个“平行宇宙”里，$L_{Cls}$(分类损失，如Focal Loss) 也在独立工作，它只负责让 $P_{cls}\to 1$。

$$L_{Total}=L_{Reg}+L_{Cls}$$

这两个损失是独立的。

问题：
一个 $IoU=0.9$的高质量Bbox，和一个$IoU=0.2$的低质量Bbox，它们都可能预测出$P_{cls}=0.99$（高置信度）。

在NMS（非极大值抑制）时，我们通常启用$P_{cls}$来排序。那个$IoU=0.2,P_{cls}=0.99$的“垃圾框”反而可能“胜出”，抑制掉$IoU=0.9,P_{cls}=0.98$的“完美框”。

为什么 $L_{Cls}$不能“感知”到$L_{Reg}$ 的质量呢？

在 【第7节：QFL质量Focal Loss与IoU感知】中，我们将“打通”这两个平行宇宙：

• “定位质量”与“分类置信度”的“不一致”（Misalignment）问题？就是什么
• QFL (Quality Focal Loss)如何重新定义“分类标签”，将$IoU$作为“软标签”引入$L_{Cls}$？
• GFL (Generalized Focal Loss) 和 DFL (Distribution Focal Loss)(YOLOv8在用!) 又是如何让模型直接预测 $IoU$分数或Bbox坐标分布的？
• 我们将揭晓YOLOv8 Bbox回归的终极秘密之一：DFL。

敬请期待！损失函数的进化，即将迎来“分类”与“回归”的“大一统”！

感谢您的坚持！$L_{InnerShape}$是一个非常前沿且艰难的概念，它已经触及了YOLOv8-Pose (姿态估计) 的核心。能理解它，说明您已经具备了“多任务学习”的视角！太棒了！

我们下期再见！

---

希望本文围绕 YOLOv8 的实战讲解，能在以下几个方面对你有所帮助：

• 模型精度提升：借助结构改进、损失函数优化、数据增强策略等，实战提升检测效果；
• 推理速度优化：结合量化、裁剪、蒸馏、部署策略等手段，支援你在实际业务中跑得更快；
• 工程级落地实践：从训练到部署的完整链路中，给出可直接复用或稍作改动即可迁移的方案。

PS：如果你按文中步骤对 YOLOv8 进行优化后，仍然遇到难题，请不必焦虑或抱怨。
YOLOv8 作为复杂的目标检测框架，效果会受到硬件环境、信息集质量、任务定义、训练配置、部署平台等多重因素影响。
要是你在实践过程中遇到：

• 新的报错 / Bug
• 精度难以提升
• 推理速度不达预期
  欢迎把 报错信息 + 关键配备截图 / 代码片段粘贴到评论区，大家可以一起分析原因、讨论可行的优化方向。
  同时，如果你有更优的调参经验或结构改进思路，也非常欢迎分享出来，大家互相启发，共同完善 YOLOv8 的实战打法

文末福利，等你来拿！

文中涉及的多数技巧问题，来源于我在 YOLOv8 项目中的一线实践，部分案例也来自网络与读者反馈；如有版权相关难题，欢迎第一时间联系，我会尽快处理（修改或下线）。
部分思路与排查路径参考了全网技术社区与人工智能问答平台，在此也一并致谢。如果这些内容尚未完全消除你的困难，还请多一点理解——YOLOv8 的优化本身就是一个高度依赖场景与数据的工程疑问，不存在“一招通杀”的方案。
如果你已经在自己的任务中摸索出更高效、更稳定的优化路径，非常鼓励你：

• 在评论区简要分享你的关键思路；
• 或者整理成教程 / 系列文章。
  你的经验，可能正好就是其他开发者卡关许久所缺的那一环

OK，本期关于YOLOv8 优化与实战应用的内容就先聊到这里。如果你还想进一步深入：

• 了解更多结构改进与训练技巧；
• 对比不同场景下的部署与加速策略；
• 系统构建一套属于自己的 YOLOv8 调优方法论；
  欢迎继续查看专栏：《YOLOv8实战：从入门到深度优化》。
  也期待这些内容，能在你的项目中真正落地见效，帮你少踩坑、多提效，下期再见

码字不易，倘若这篇文章对你有所启发或帮助，欢迎给我来个一键三连（关注 + 点赞 + 收藏），这是我持续输出高质量内容的核心动力

同时也推荐关注我的公众号「猿圈奇妙屋」：

• 第一时间获取 YOLOv8 / 目标检测 / 多任务学习 等方向的进阶内容；
• 不定期分享与视觉算法、深度学习相关的最新优化方案与工程实战经验；
• 以及 BAT 等大厂面试题、技术书籍 PDF、工程模板与工具清单等实用资源。
  期待在更多维度上和你一起进步，共同提升算法与工程能力

Who am I?

我是专注于 计算机视觉 / 图像识别 / 深度学习工程落地的讲师 & 技术博主，笔名bug菌：

• 活跃于 CSDN | 掘金 | InfoQ | 51CTO | 华为云 | 阿里云 | 腾讯云等技术社区；
• CSDN 博客之星 Top30、华为云多年度十佳博主、掘金多年度人气作者 Top40；
• 掘金、InfoQ、51CTO 等平台签约及优质创作者，51CTO 年度博主 Top12；
• 全网粉丝累计30w+。

通过更多系统化的学习路径与实战资料能够从这里进入 点击获取更多精彩内容
硬核技术公众号「猿圈奇妙屋」欢迎你的加入，BAT 面经、4000G+ PDF 电子书、简历模版等通通可白嫖，你要做的只是——愿意来拿

-End-