深入解析:排序算法大全
0. 前言
以下代码均通过了这道题 912. 排序数组 - 力扣(LeetCode) ,代码质量是可以保证的。
在具体讲解算法之前,我们先补充几个小知识!
1. 时间复杂度(《大话数据结构》 这本书中的解释)

2. 空间复杂度
描述算法所需额外空间随输入数据规模增长的变化趋势(额外空间 = 算法执行过程中临时占用的空间,不包括输入数据本身的空间)。
简单来说就是:当处理的数据量变大时,算法需要额外占用多少内存?
举个例子:原地排序(冒泡排序、插入排序)、遍历数组时只使用几个临时变量(比如计算数组总和)、修改数据时直接在原对象上操作。 这个空间复杂度为O(1)
3. 稳定性
仅针对排序算法,指:排序后,相等元素的相对顺序保持不变。
比如数组 [3, 2, 2, 1],排序后若为 [1, 2, 2, 3],且原来两个 2 的位置没有交换,则是稳定排序;若变成 [1, 2(原来的第二个2), 2(原来的第一个2), 3],则是不稳定排序。
1.冒泡排序
核心思路:
冒泡排序:像在海里的气泡一样,最底下的最小,越往上越大。在这里我们比较左右两数字(也可以说是上、下两个气泡),大的在右(上),小的在左(下),不对的我们交换一下。
在每一轮的交换结束都可以确定一个数的位置。
//1.冒泡排序
public int[] bubbleSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n - 1; i++) { // 比较的趟数 每一趟确定一个最大的数
int check = 0;
for (int j = 0; j < n - i - 1; j++) {//每一趟固定无序数中的一个最大的数
if (arr[j] > arr[j + 1]) { // 交换
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
check = 1;
}
}
if (check == 0) {// 如果check = 0, 说明数组已经有序!
break;
}
}
return arr;
}2.插入排序
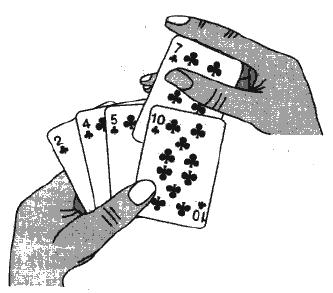
核心思路:扑克牌我们都玩过,玩家轮流从牌堆里取一张牌,手里的牌是有序的,现在插入一张,使整体仍然有序。
/**
* 插入排序
*/
public int[] insertionSort(int[] arr) {
int n = arr.length;
for (int i = 1; i < n; i++) {
int temp = arr[i];
int index = i;
//找到要插入的位置
for(int j = i; j > 0; j--) {
if(arr[j - 1] < temp) {
break;
}
index--;
}
//后移,腾出位置
for(int j = i; j > index;j--){
arr[j] = arr[j-1];
}
// 插入
arr[index] = temp;
}
return arr;
}如下对找位置和插入进行优化:
//2.插入排序
/* 改进
* 插入排序是在有序数组中,再插入一个
* */
public int[] insertionSort1(int[] arr) {
int n = arr.length;
for (int i = 1; i < n; i++) {
int tep = arr[i];
for(int j = i; j > 0; j--) {
if(tep >= arr[j-1]) {
arr[j] = tep; // 插入
break;
}else {
arr[j] = arr[j-1]; //后移
}
}
if(tep < arr[0]) arr[0] = tep; // 0 位置特殊处理
}
return arr;
}3.选择排序
核心思路:我们开启了上帝视角,每次从一堆无序数中选出一个最小的加入到有序数中,当无序数堆没有了,我们便获取了一组有序数。
//选择排序
public int[] selectionSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n - 1; i++) { //选择的趟数
int tep = arr[i];
int index = i;
for (int j = i + 1; j < n; j++) {
if(arr[j] < tep) {
index = j;
tep = arr[j];
}
}
if(index != i) {
arr[index] = arr[i];
arr[i] = tep;
}
}
return arr;
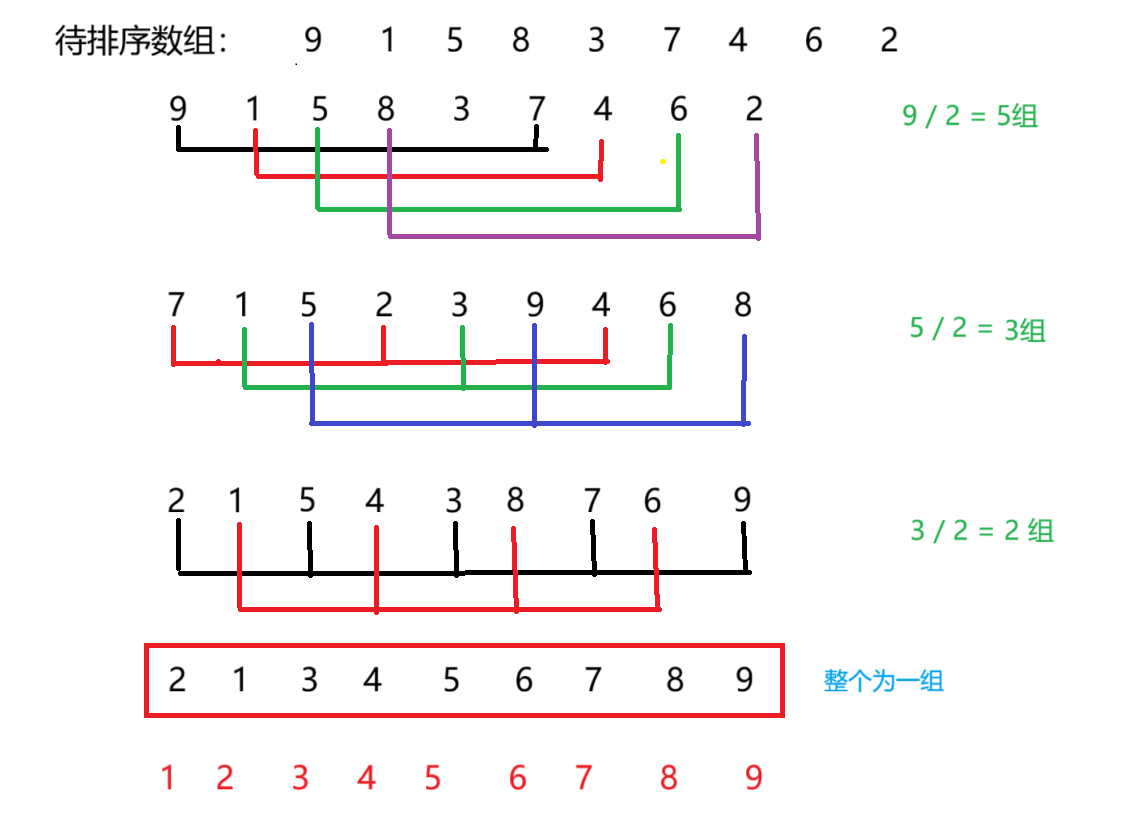
}4.希尔排序
核心思路:分组排序,组内插入排序。
/**
* 希尔排序
* 对于希尔排序我更喜欢称它为:分组排序,组内插入排序
*/
public int[] shellSort(int[] arr) {
int n = arr.length;
int interval = n; // 间隔 等于 分组数
int stand = 2;
do {
interval = interval / stand;
for (int i = 0; i < interval;i++){// 分组
for (int j = i + interval;j < n;j += interval){ //组内排序
// 组内插入排序
int tep = arr[j];
for (int k = j;k - interval >= 0;k -= interval){
if(arr[k - interval] < tep){
arr[k] = tep; // 插入
break;
}else{
arr[k] = arr[k - interval]; // 后移
}
}
if(tep < arr[i]) arr[i] = tep; // 每组第一个位置特殊处理
}
}
}while (interval > 1);
return arr;
}5.堆排序
利用堆这种数据结构。
- 大顶堆:每个父节点的值 ≥ 其左右子节点的值 → 堆顶(根节点)是整个堆的最大值;
- 小顶堆:每个父节点的值 ≤ 其左右子节点的值 → 堆顶是整个堆的最小值。
/**
* 堆排序
*/
public int[] heapSort(int[] arr) {
int n = arr.length;
PriorityQueue pq = new PriorityQueue<>();
for (int i = 0; i < n; i++) {
pq.offer(arr[i]);
}
for (int i = 0; i < n; i++) {
arr[i] = pq.poll();
}
return arr;
} 6.归并排序
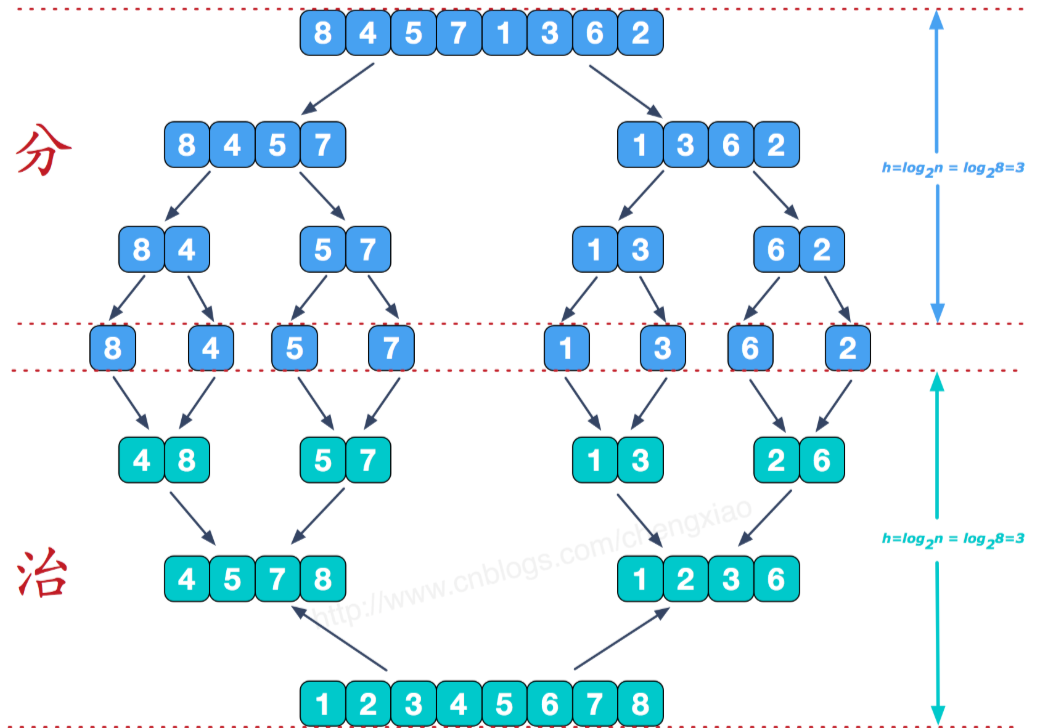
核心思路:两个基本的操作,一个是分,也就是把原数组划分成两个子数组的过程。另一个是治,它将两个有序数组合并成一个更大的有序数组。
- 将待排序的线性表不断地切分成若干个子表,直到每个子表只包含一个元素,这时,可以认为只包含一个元素的子表是有序表。
- 将子表两两合并,每合并一次,就会产生一个新的且更长的有序表,重复这一步骤,直到最后只剩下一个子表,这个子表就是排好序的线性表。
/**
* 归并排序
* 准确的说是:二路归并
*/
public int[] mergeSort(int[] arr) {
int n = arr.length;
mSort(0,n-1,arr);
return arr;
}
private void mSort(int l, int r, int[] arr) {
if(l >= r) return;
int mid = (l+r)/2;
mSort(l,mid,arr);
mSort(mid+1,r,arr);
merge(l,mid,r,arr);
}
private void merge(int l, int mid, int r, int[] arr) {
int[] array = new int[r-l+1];
int index = 0;
int i = l,j = mid + 1;
for(;i <= mid && j <= r;){
if(arr[i] < arr[j]){
array[index++] = arr[i++];
}else {
array[index++] = arr[j++];
}
}
for(;i <= mid;i++){
array[index++] = arr[i];
}
for(;j <= r;j++){
array[index++] = arr[j];
}
for (int ii = 0; ii < array.length; ii++ ) {
arr[l++] = array[ii];
}
}7.快速排序
核心思路:选择一个基准元素(base),通常选择第一个或最后一个元素,然后对数组进行分区操作,使得:
比基准元素小的元素都移到基准的左边
比基准元素大的元素都移到基准的右边 这个过程称为一趟快速排序。
快速排序算法—图文详解,一篇就够了!-CSDN博客 (过程参考这个)
/**
* 快速排序
* 三数取中版
*/
// TODO 第一版
public int[] quickSort(int[] arr) {
int n = arr.length - 1;
qSort(0,n,arr);
return arr;
}
private void qSort(int l, int r, int[] arr) {
if(l >= r) return;
int mid = l + (r - l) / 2;
int standardIndex = findMiddle(l,mid,r,arr);
int standard = arr[standardIndex];
swap(r,standardIndex,arr);
int i = l,k = r;
while(i < k){
while (i < k && arr[i] < standard){
i++;
}
while (i < k && arr[k] >= standard){
k--;
}
swap(i,k,arr);
}
swap(i,r,arr);
qSort(l,i - 1,arr);
qSort(i + 1,r,arr);
}
private void swap(int l, int mid, int[] arr) {
int tep = arr[l];
arr[l] = arr[mid];
arr[mid] = tep;
}
private int findMiddle(int l, int mid, int r, int[] arr) {
if(arr[l] >= arr[r]){
if (arr[mid] > arr[l]) return l;
if(arr[r] > arr[mid]) return r;
return mid;
}else {// r > l
if(arr[mid] > arr[r]) return r;
if(arr[l] >= arr[mid]) return l;
return mid;
}
}
private int findMiddle(int l, int mid, int r, int[] arr) {
if((arr[l] - arr[mid]) * (arr[l] - arr[r]) <= 0) return l;
if((arr[mid] - arr[l]) * (arr[mid] - arr[r]) <= 0) return mid;
return r;
}
//TODO: 第二版
/**
* 对于快速排序中:挖坑法、前后指针法、左右指针法 使用 三数取中,达到一定的优化
* 但仍然多多少少还有一些瑕疵, 1,2,6,8,5,5,5,5,5,5,1,1,1
* 向这些有重复的,便会多次的被排序
* 这里采用三路划分 (效率最高)
*/
public int[] quickSort(int[] arr) {
int n = arr.length - 1;
qSort(0,n,arr);
return arr;
}
private void qSort(int l, int r, int[] arr) {
if(l >= r) return;
int standard = arr[l + new Random().nextInt(r - l + 1)];
int left = l - 1;
int right = r + 1;
for (int i = l; i < right; ) {
if(arr[i] < standard) {
swap(++left,i++,arr);
}else if(arr[i] == standard){
i++;
}else{
swap(--right,i,arr);
}
}
qSort(l,left,arr);
qSort(right,r,arr);
}
private void swap(int l, int mid, int[] arr) {
int tep = arr[l];
arr[l] = arr[mid];
arr[mid] = tep;
}如上便是今天的分享了!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号