数据结构——五十二、散列函数的构造(王道408) - 实践

文章目录

• 前言
• 一.设计散列函数时应该注意什么
• 二.除留余数法
• • 1.思路和运用场景
  • 2.具体例子
  • 3.拓展：为什么除留余数法要对质数取余？
  • • 1.原因
    • 2.具体例子
• 三.直接定址法
• • 1.思路与使用场景
  • 2.具体思路
• 四.数字分析法
• • 1.思路与使用方法
  • 2.具体例子
• 五.平方取中法
• • 1.思路与使用方法
  • 2.具体例子
• 六.知识回顾与重要考点
• 结语

前言

本文总结了设计散列函数的注意事项和常用方法。设计散列函数时需注意：定义域覆盖所有关键字、值域不越界、减少冲突、计算方便。首要方法包括：除留余数法（取不大于表长的最大质数）、直接定址法（适用于连续关键字）、数字分析法（选取分布均匀的数码位）、平方取中法（取平方值的中间位）。其中重点阐述了除留余数法对质数取余可减少冲突的原因，并依据具体示例说明了各技巧的适用场景和达成要点。这些手段可根据关键字特性选择使用，以达到均匀分布和高效存储的目的。

一.设计散列函数时应该注意什么

1. 定义域必须涵盖所有可能出现的关键字。
   反例：$H(key)=\sqrt{key}\%13$,不帮助关键字为负值

2. 值域不能超出散列表的地址范围。
   反例:$H(key)=key\%15$，可能被映射到非法地址13、14

3. 尽可能减少冲突。散列函数计算出来的地址应尽可能均匀分布在整个地址空间。
   反例:$H(key)=(key\times 13)\%13$任何关键字都会被映射到地址0

4. 散列函数应尽量方便，能够快速计算出任意一个关键字对应的散列地址。
   反例：$H(key)=(key!)\%13$，若关键字值较大，计算阶乘耗时高

二.除留余数法

1.思路和启用场景

• $除留余数法——H(key)=key\%p$
  散列表表长为m，取一个不大于m但最接近或等于m的质数p
  注：质数又称素数。指除了1和此整数自身外，不能被其他自然数整除的数
• 适用场景：较为通用，只要关键字是整数即可

2.具体例子

• 质数，因此可令散列函数 H(key)=key%13就是例1：散列表表长 m=13。13
  
• 例2：散列表表长 m=15。不大于15且最接近15的质数是13，因此可令散列函数 H(key)=key%13

3.拓展：为什么除留余数法要对质数取余？

1.原因

• 原因：对质数取余，可以分布更均匀，从而减少冲突

2.具体例子

• 设：可能出现的关键字={2,4,6,8,10,12,14}

1. 散列表表长8，散列函数H(Key)=key%8
   

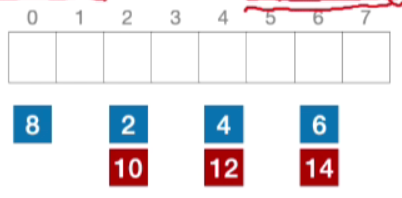
• 对合数取余，散列地址分布不均匀，易发生冲突

1. 散列表表长8，散列函数H(Key)=key%7
   

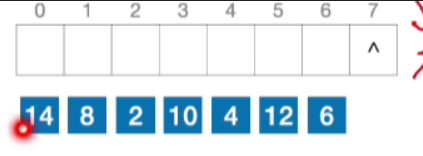
• 对质数取余，散列地址分布均匀，不易发生冲突

Why？——取余运算会被“公因子”影响，详见《数论》

三.直接定址法

1.思路与使用场景

• 直接定址法——$H(key)=key或H(key)=a\ast key+b$
  其中，a和b是常数。此种办法计算最简单，且不会产生冲突。若关键字分布不连续，空位较多，则会造成存储空间的浪费。
• 适用场景：关键字分布基本连续

2.具体思路

• 例：用散列表存储某班级的30个学生信息，班内学生学号为(1120112176~1120112205)
• 可令 H(key) = key - 1120112176

四.数字分析法

1.思路与使用方法

• 数字分析法——选取数码分布较为均匀的若干位作为散列地址
  r进制数 (如十进制数)，而r个数码在各位上出现的频率不一定相同，可能在某些位上分布均匀一些，每种数码出现的机会均等；而在某些位上分布不均匀，只有某几种数码经常出现，此时就是设关键字可选取数码分布较为均匀的若干位作为散列地址。
• 适用场景：关键字集合已知，且关键字的某几个数码位分布均匀

2.具体例子

• 例：要求将手机用户的信息存入长度为 10000 的散列表。以“手机号码”作为关键字设计散列函数
  1. 中国移动联通电信前三位电话号码各不一样,中间的四位通常是地区的区号,而末尾的四位每个人的电话号码就各不相同
  2. 所以以手机号码作为关键字的话,那前边的这七个数码位,这些值的分布是不均匀的,只有末尾的四个数码位它的分布是相对均匀的,那我们可以直接选取末尾的四位作为散列地址
     

五.平方取中法

1.思路与使用方法

• 平方取中法——取关键字的平方值的中间几位作为散列地址。
  具体取多少位要视实际情况而定。这种方法得到的散列地址与关键字的每位都有关系，因此使得散列地址分布比较均匀。
• 适用场景：关键字的每位取值都不够均匀。

2.具体例子

• 例：某汽车品牌，以（底盘号、发动机号、外观号）作为一款汽车型号的标识。该品牌有100种车型，欲将这些车型信息存入长度为100的散列表，如何设计散列函数？
  1. 先对关键字取平方
     
  2. 我们取平方的中间两个数值位作为散列地址
     
• 原因是在乘方的时候最中间的两位元素会受到其它所有元素的影响,在这种情况下,最中间的两位元素最终会分布的相对均匀

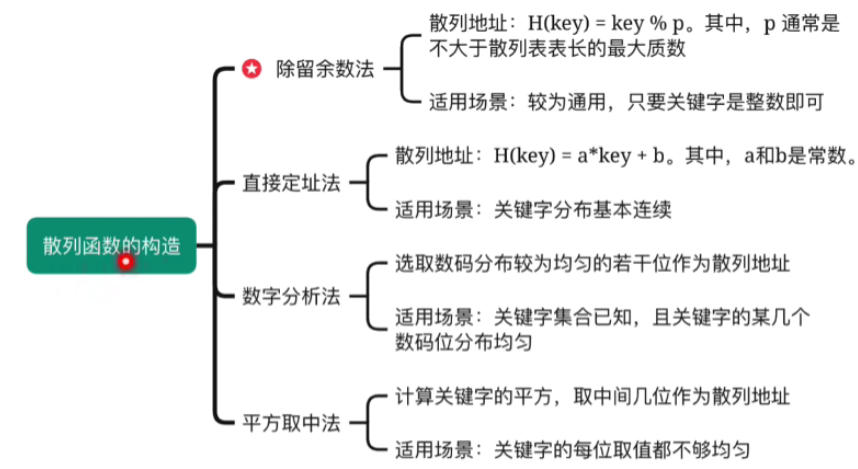
六.知识回顾与重要考点

结语

八更

如果想查看更多章节,请点击:一、数据结构专栏导航页