AIGC 论文笔记 - 详解

图像生成

一、GAN

GAN有两个模型，模型G (Generator) 负责拟合训练材料的分布 (也就是拟合概率密度)，模型D (Discriminator) 负责评估一个样本是来自训练数据还是来自G的概率，在训练过程中G要尽可能骗过D，而D要尽可能分辨出G生成的样本。两个模型都是MLP，在对抗的过程中得到训练，最终的理想情况是G生成的分布完全拟合训练数据的分布，并且D无法分辨二者 (输出永远是1/2).

1. 对抗模型

设G的分布为pg (p代表概率密度)，其随机变量为x，定义一个噪音变量z (直接从先验分布 (如高斯分布) 中采样得到)，同时也是隐变量，G(z)的作用是将z映射到x. (以800万像素的游戏图片生成为例，假设z是100维的向量，代表游戏中人物地点等变量，x为800万维的向量，代表800万像素点，G就负责将z映射到x)。而D的输出是一个标量，D(x)表示x是来自训练数据的概率。我们的目标是训练D以最大化给来自训练信息的样本 (x ~ pdata) 和G生成的样本 (G(z) ~ pg) 打上正确标签的概率，在公式中表示就是最大化logD(x)的期望和log(1 - D(G(z)))的期望；同时训练G以最小化log(1 - D(G(Z)))，在公式中表示就是最小化log(1 - D(G(z)))的期望。不过在训练的早期G还很弱，D(G(z))趋于0，log(1 - D(G(z)))的梯度会非常小，不利于训练，如果改为最大化logD(G(z))就会好很多。

GAN的价值函数

GAN的算法伪代码

下图是GAN的训练过程，黑点是训练数据，绿色实线是G生成的分布，由z映射而来，蓝色虚线是D的输出。(a) 是最初的状态，pg与pdata相差较大，D的输出正确率低；(b) 是D经过训练后能很好地分辨pg和pdata；(c) 是G经过训练后为了骗过D使pg更加拟合pdata；(d) 是最终的状态，pg完全拟合pdata，D的输出始终是1/2.

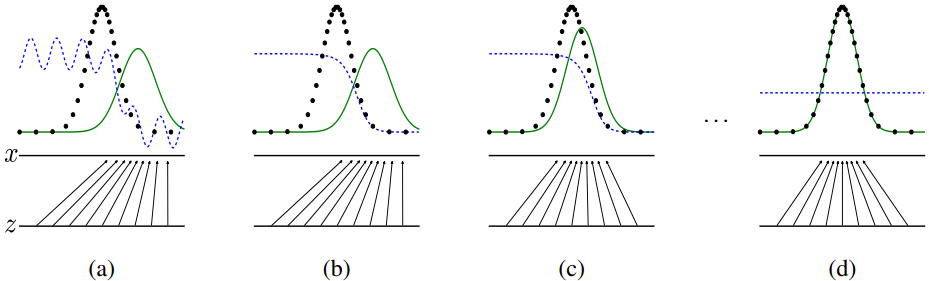
GAN的训练过程

2. 理论结果

1）最优的D

在给定G的情况下，最优的D为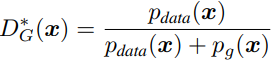，其中p(x)表示某个x在该分布中的概率密度。证明如下：使a*log(y) + b*log(1-y)取最大值，当且仅当y = a/(a+b)时满足就是要使V这个积分最大，就，也就是D(x) = pdata(x) / (pdata(x) + pg(x)).

可以发现当pdata与pg完全拟合时D*输出恒为1/2.

2）最优的G

将最优的D代入到价值函数中，会得到如下式子：

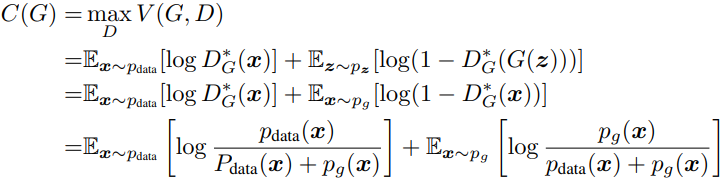
对两个log进行如下变形

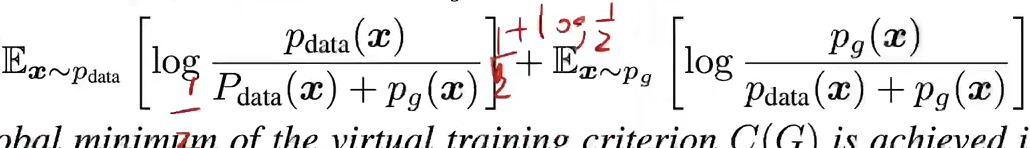
pdata和(1/2)*pdata+pg这两个分布的KL散度，写成如下形式，由于就是行发现这就KL散度大于等于0，当且仅当pdata = pg时取0，故pdata = pg时C(G)最小，也就是G最优。

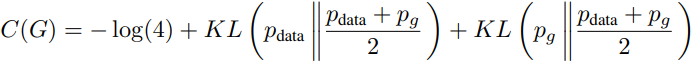
补充知识：KL散度，描述两个分布的相似程度的量，定义如下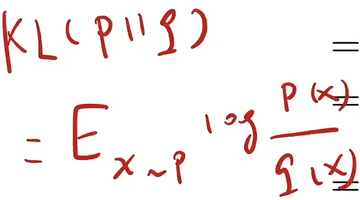，表示p和q两个分布的KL散度。

3）对抗收敛

在对抗过程中如果每次D和G都能到最优，则最终pg会收敛于pdata. 证明略。

3. 未来工作

① 条件生成模型 (Conditional Generative Model): 依据将条件变量 c 作为输入添加到生成器 G 和判别器 D 中，允许得到一个条件生成模型 p(x∣c)，即生成的样本 x 是基于条件 c 的；

② 近似推断 (Learned Approximate Inference): 可以训练一个辅助网络来预测在给定观测数据 x 下时的隐变量 z。推断网络可以在生成器网络训练完成后进行训练。通过预测 z，可以将隐变量与某个条件或特征相关联，从而控制生成过程；

③ 半监督学习 (Semi-Supervised Learning)通过: 判别器或推断网络的特征能够在有限标注内容的情况下提高分类器的性能；

④ 效率改进 (Efficiency Improvements): 训练过程的效率可以通过优化生成器和判别器的协调途径，或者改进训练过程中采样隐变量 zzz 的分布来大幅提高。

二、VAE

VAE的最终目标是要找到观测数据的最大似然分布pθ(x)，然后可以从该分布中采样进行生成。不过对于图像这样的数据，直接建模用最大似然找pθ(x)是不现实的，因此要引入隐变量 (Latent Variable) z的概念 (隐变量是观测不到但对观测内容有影响的反映其潜在信息的数据，维度比观测信息小，比如一个圆的图像，隐变量就是圆心和半径此种隐藏的素材)。有了隐变量之后，x的似然就变成了边缘似然，pθ(x) = ∫ pθ(x,z) dz = ∫ pθ(z)pθ(x|z) dz，这个积分计算不了，考虑贝叶斯公式，有后验分布pθ(z|x) = pθ(x|z)pθ(z)/pθ(x)，则pθ(x) = pθ(x,z)/pθ(z|x)，但是这个后验分布同样也计算不了，于是采用变分推断 (Variational Inference) 用另一个分布 qϕ​(z∣x) 去近似后验分布，而两个分布的相似度允许用KL散度来描述，将KL散度的式子进行一些变形，可以化出一个log pθ(x)，换一下位置，得到x的似然函数。

注：在训练阶段z是从近似后验分布qϕ​(z|x)中得到的，而推理阶段z是从先验分布pθ(z)中采样出来的，先验分布通常直接取标准高斯分布N(0,I)

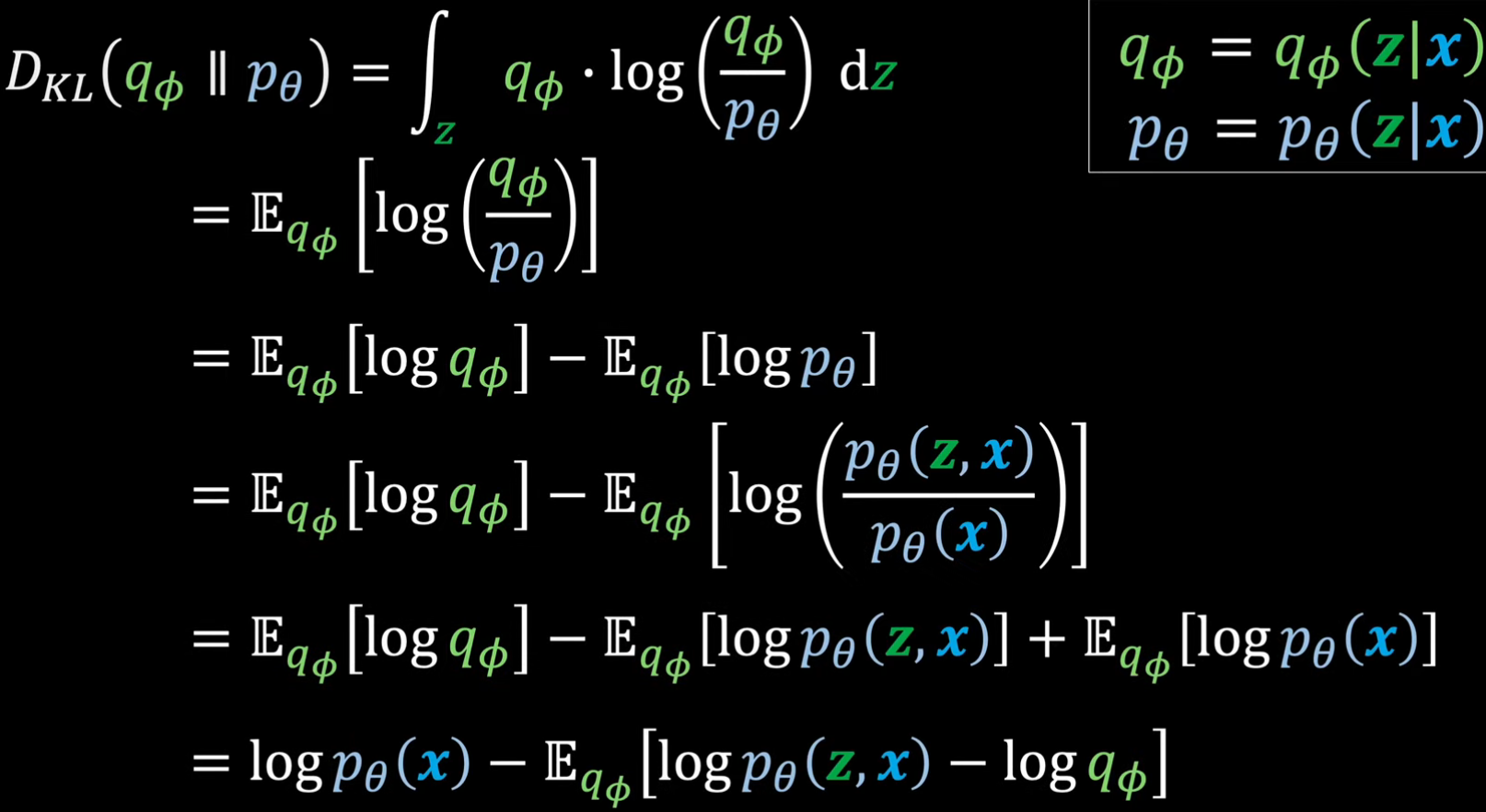
1. Objective Function

我们的目标是最大化该似然函数，由于KL散度 ≥ 0，因而log pθ(x) ≥ Eqφ(z|x) [− log qφ(z|x) + log pθ(x, z)]，我们将右边称为ELBO (Evidence Lower Bound)，可以发现凭借优化θ和ϕ使ELBO变大，会让log pθ(x)变大，KL散度变小，这正是我们的目标，因此ELBO就是目标函数L(θ, φ; x)就. 继续将ELBO展开并变形，可以将其化为一个重构损失减去KL散度的形式。这个目标函数的梯度是可以通过一些推导估算出来的，这里省略这些推导。

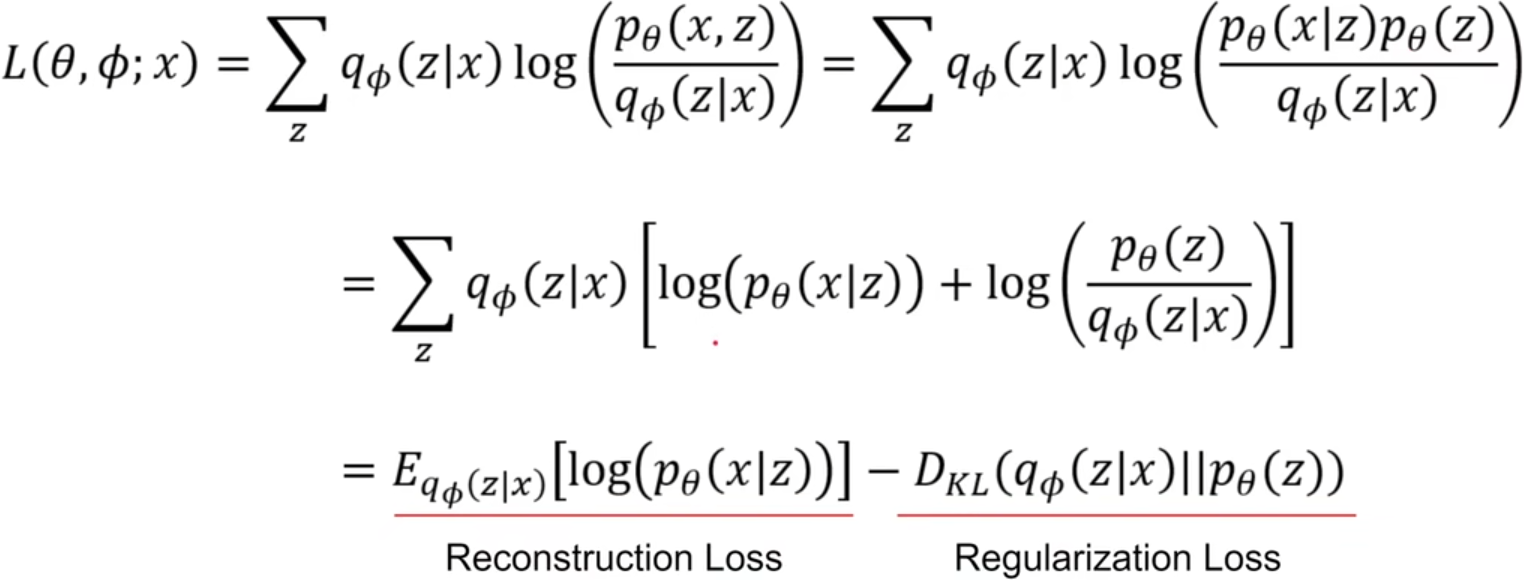
ELBO、似然函数、KL散度的关系

2. Reparameterization

训练时隐变量z是从分布 qφ(z|x) 中采样出来然后进行后续正向传播的，这样就导致梯度没法回传，作者在这里采用了重参数化 (Reparameterization)的技巧，通过引入一个与θ和φ都无关的随机变量ϵ，通常服从N(0,I)，z是x, φ, ϵ三者的函数，即z = gφ(ϵ, x) (实际上是先由x和φ确定分布q的期望μ和方差Σ，然后由μ, Σ, ϵ三者得到z，如z = µ + Σϵ)，这样就将随机性让ϵ承担了通过，梯度就能够回传给φ这些参数上了。

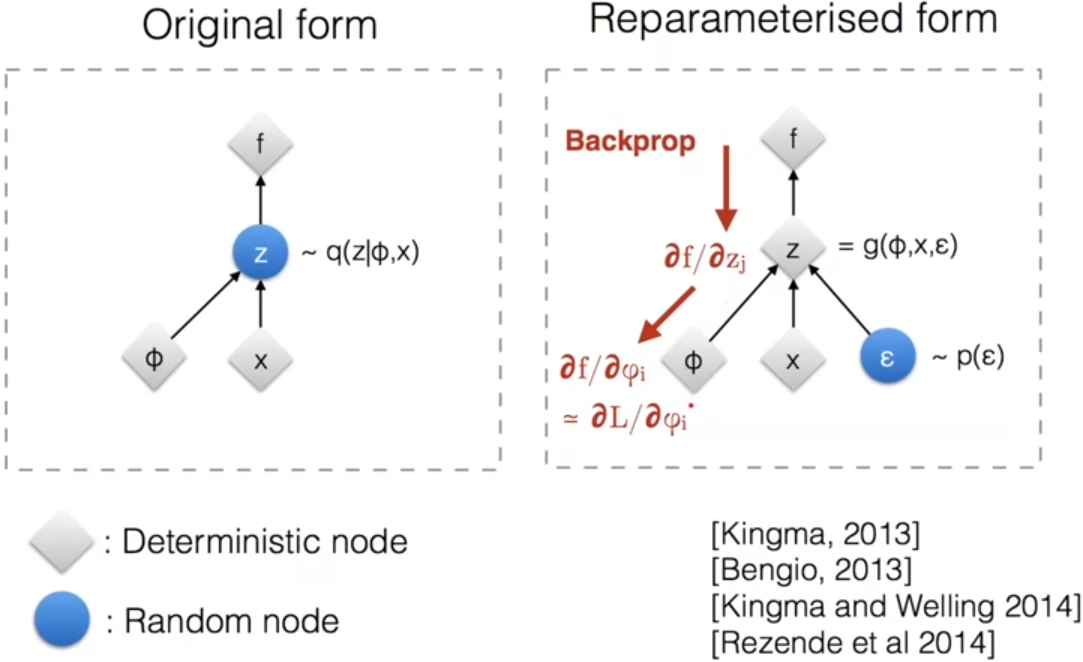
重参数化示意图

3. Model Architecture

下图就是VAE的整体网络结构，是一个Encoder-Decoder架构，其中φ是encoder的参数，θ是decoder的参数。整个前向过程大致是：将x放入encoder得到近似后验分布qϕ​(z∣x)的期望μ和方差Σ，然后结合随机采样的变量ϵ得到z，将z放入decoder得到还原出来的xr，然后计算x与xr的重构损失 (这里是MSE)，再减去根据μ和Σ计算出的KL散度，得到最终的Loss.

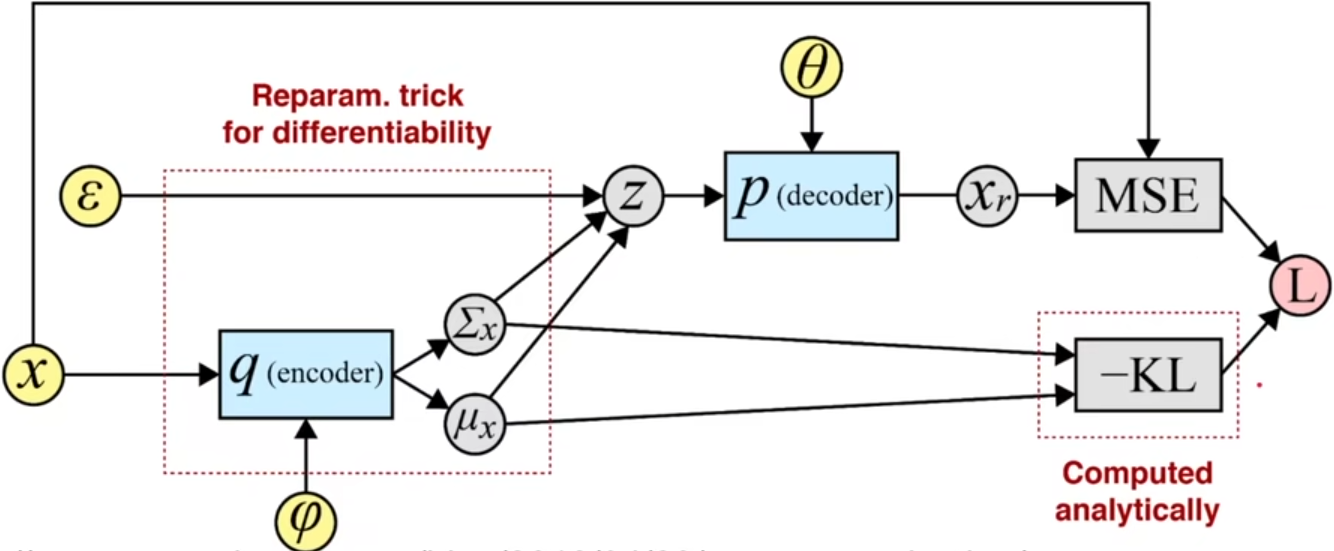
4. 未来工作

① 学习分层生成架构：行将网络设计成分层结构，让模型能够高效地学习隐变量分布，捕捉数据中的层次化特征；

② 带有隐变量的监督模型：在标签或数据存在噪声、不确定性或缺失的情况下，通过将隐变量引入到监督学习任务中，模型可以学习到数据的潜在结构和噪声的分布，从而提高模型的鲁棒性和泛化能力。

三、VQ-VAE

VQ-VAE 是一种生成模型，它将VAE中的连续隐变量空间替换为一个离散的隐变量空间 (即码本$Z_e$)，从而能更好地建模具有离散潜在结构的复杂数据。

我们可以将其结构概括为：VQ-VAE = Encoder + Decoder + Codebook

1. Model Architecture

VQ-VAE 的核心在于向量量化 (Vector Quantization, VQ)，它发生在编码器输出$z_e$和解码器输入$\hat{z}$ 之间。

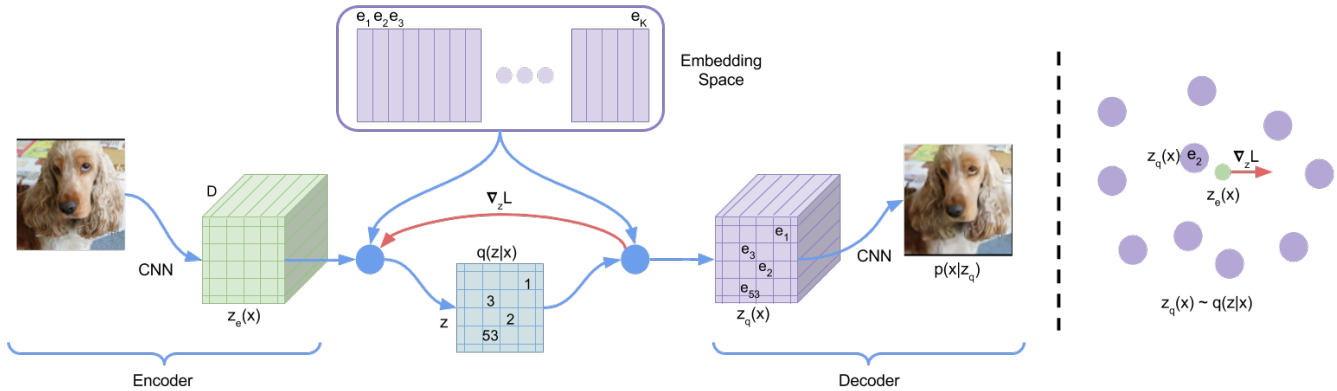
VQ-VAE 架构图

  1. 码本 (Codebook)$e$： 这是一个由$K$个向量 $\{e_1, e_2, \dots, e_K\}$组成的集合，这些向量是可学习的参数。

  2. 量化运行 (Vector Quantization)：

  • 目标：将编码器$E$产生的连续特征$z_e$ 映射到码本 $e$中的一个离散向量。
  • 步骤：对于 $z_e$中的每一个特征向量，执行最近邻查找：
    • 找到索引 $k$：在码本 $e$ 中，找到与 $z_e$欧氏距离最小的码字 $e_k$;
    • 赋值：量化后的隐变量$\hat{z}$就等于这个选定的码字$e_k$.

  • （其中 $|| \cdot ||$代表欧氏距离。）

2. Objective Function

VQ-VAE 的总损失函数旨在同时训练编码器、解码器和码本：

Total Loss = L_reconstruction + L_commitment + L_codebook

1) 重构损失（Reconstruction Loss）

  • 目的：确保解码器能从量化后的$\hat{z}$中还原出原始图像$x$.
  • 形式（运用 MSE）：

  • （表示：原始图像$x$与解码器重构图像的平方距离的期望。）

2) 码本损失（Codebook Loss）

  • 目的：更新码本 $e$的参数，使其向编码器输出$z_e$ 靠近。

  • （表示：量化后的$\hat{z}$与编码器输出$z_e$的平方距离。在反向传播时，梯度只更新码本$e$，不更新 $z_e$.）

3) 承诺损失（Commitment Loss）

  • 目的：更新编码器 $E$的参数，鼓励$z_e$靠近它选择的码字$\hat{z}$.
  • 形式：引入超参数$\beta$ (通常 $\beta=0.25$)。

  • （表示：编码器输出$z_e$ 与量化后的 $\hat{z}$的平方距离。在反向传播时，梯度只更新编码器$E$，不更新 $\hat{z}$.）

    3. 生成过程

    VQ-VAE 作为一个两阶段生成模型，其生成步骤如下：

    1. 第一阶段：提取离散索引

      • 训练 VQ-VAE，并使用其编码器$E$提取训练图像的离散码本索引地图$Z_{\text{index}}$.

    2. 第二阶段：学习索引分布

      • 训练一个自回归模型（如 Transformer）来学习上述离散索引地图$Z_{\text{index}}$ 的联合概率分布$p(Z_{\text{index}})$.

    3. 推理阶段：生成样本

      • 使用训练好的自回归模型 采样生成一个新的离散索引地图$Z_{\text{index}}'$.

      • 将 $Z_{\text{index}}'$转换为对应的码字$\hat{z}'$(经过查码本$e$).

      • 使用 VQ-VAE 解码器$D$ 将 $\hat{z}'$还原成最终图像$\hat{x}'$.

    四、DDPM

    扩散模型是从采样得到的噪音变量生成目标资料样本，其模型包括两个过程：正向过程 (forward process) 和反向过程 (reverse process)，其中正向过程又称为扩散过程 (diffusion process)，指根据分布 q(xt|xt-1) 往图像中一步步加噪声(实际上是由预定义好的分布直接生成某一步的噪声图像)；而反向过程是根据分布 pθ(xt-1|xt) 将噪声图像逐步去噪直到恢复成原图像。无论是正向过程还是反向过程都是一个马尔可夫链 (Markov Chain，状态转移时下一状态的概率分布只由当前状态决定，而与之前的状态都无关)，其中正向过程是固定的，没有要训练的网络，而反向过程要训练一个网络 (通常是U-Net)，并且每个step共享这个网络。

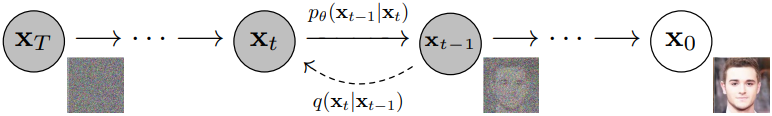
    扩散模型基本结构

    另外扩散模型也可以用概率路径和流匹配的角度来解释，目前的SOTA模型也是基于这种角度，详见流匹配与扩散模型。

    1. Forward Process

    正向过程 (或扩散过程) 是一个固定的马尔可夫链，没有要学习的参数，每一步根据方差调度β1, ..., βT来增加高斯噪音，即，其目的是将数据分布逐渐变为标准高斯分布 N(0,I)，整个正向过程的联合分布可表示为状态转移的累乘，即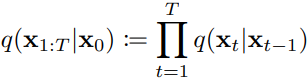. 由于正向过程每一步的分布都是由固定的β超参数确定的，经过计算可以直接得到任意一步分布的闭式：定义.则有.

    2. Reverse Process

    反向过程从一个噪声图像xT开始，这张噪声图像从先验标准高斯分布中采样得到，即一个高斯分布，其就是. 每次去噪的状态转移也期望方差由当前状态xt，参数θ，以及t (即time embedding，给每次去噪加入步数的信息，使不同步数去噪时关注不同的地方) 决定，即，这是对正向过程的逆条件分布也就是真实后验分布的拟合。整个反向过程是一个马尔可夫链，能够表示为所有状态转移的累乘，即.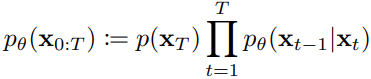

    3. Objective Function

    根据前面的定义可以写出负对数似然的上界，也就是似然的ELBO，并将其作为损失函数。

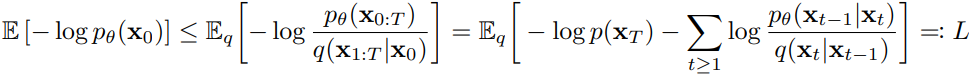
    代入正向过程的闭式改写ELBO：

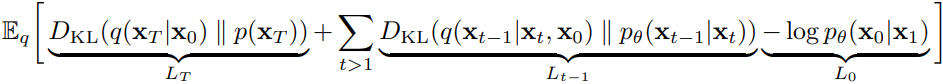
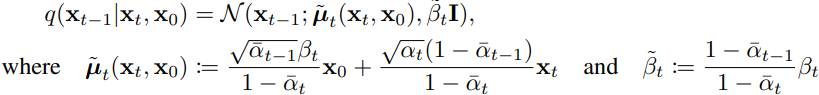
    ，其中没有x0的，只能用于训练)。就是就是大家要拟合的真实后验分布 (不直接使用这个分布是因为它需要x0，而推理时

    由于式中的LT与θ无关的，L0是最后一步降噪很小可以忽略，故ELBO可以只保留所有的Lt （t>1)，即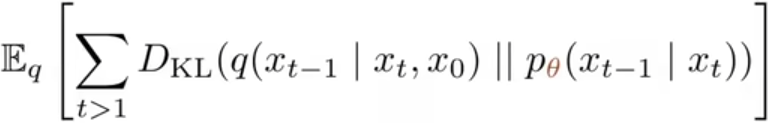：. 也就是所有真实后验分布与近似后验分布的KL散度之和的期望。

    为了进一步简化，作者将pθ的方差Σ固定为σt^2，即与t有关的常数，经过实验就是(其中σt和效果差不多)，从而两个后验分布的KL散度就行简化为两个分布的均值μ的简单平方距离：.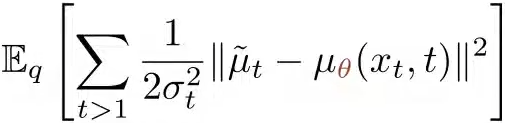

    但是的表达式还是有点复杂，作者启用VAE中的重参数化技巧，将xt写成x0与一个采样自标准高斯分布的随机噪声ϵ的和：，然后再进行变形，得到x0：，将其代入原表达式，得到. 再将同样的技巧应用到μθ上，得到. 最后将两个表达式代入到损失函数中，得到最终的损失函数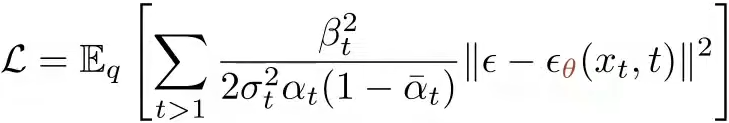. 也就是实际噪声与预测噪声的平方距离，这就将目标转变为了预测噪声(注意这个噪声是x0与xt之间的噪声，不是xt-1与xt之间的噪声)，而不是预测一整张图像。

    通过另外在训练时对每个样本的所有t时间步都求和计算成本太高，能够选择对每个样本只随机选择一个时间步进行损失计算，即.

    这里推导得到的是带复杂权重的损失，而作者实验发现，直接用均方误差（不加权），实际上会让模型“自动忽略容易的小噪声任务，多关注困难的大噪声任务”，从而提升生成质量。

    4. 伪代码

    DDPM的训练和采样 (推理) 的伪代码如下：

    其中推理时去噪高斯采样是

    ，即.

    5. 与VAE的对比

    DDPM 和 VAE 的核心联系在于它们都源自变分推断（Variational Inference），并都试图最大化数据的对数似然下界 (Evidence Lower Bound, ELBO) 。

    潜变量模型 (Latent Variable Model)：

    • VAE：将数据 x 映射到一个低维潜变量 z。其过程是 x -> z -> x'。

    • DDPM：将数据 x0 映射到一个与 x0同维度的、完全是噪声的潜变量 xT。其过程是 x0 -> x1 -> ... -> xT（前向过程，即编码器），然后 xT -> ... -> x0'（反向过程，即解码器）。

    编码器-解码器结构 (Encoder-Decoder):

    • 编码器 q (前向过程)：在 DDPM 中是固定的马尔可夫链（通过添加高斯噪声）。这与 VAE 中应该学习的编码器 qΦ(z|x) 形成了显著的差异。

    • 解码器 pθ (反向过程)：DDPM 用一个神经网络 θ（通常是 U-Net）来学习从 xt 到 xt-1 的反向转移，这相当于 VAE 中的解码器

    因此，DDPM 允许被称为一种多步骤 VAE (Multi-step VAE)，它将编码和解码过程分解成了许多小的、固定步长（编码）和学习步长（解码）的步骤。不同的是

    • VAE生成质量样本通常较为模糊，但速度极快
    • DDPM样本通常具有极高的保真度，但生成速度较慢 (需 T 步)

    另外由于低纬度就是VAE的潜变量，许可压缩信息学到抽象特征，而和输入同纬度就是DDPM的，导致 VAE 比 DDPM 更适合表征学习，从而更适合多模态理解和生成的统一。例如 VAE 可以将文本和图像都映射到这个共享的 z 空间，我们能够用 zText 来指导图像解码器 pθ(xImage| zText) 建立文本到图像的生成。

    五、DALL·E 2

    DALL·E 2使用 CLIP 提取图像文本对内容的文本特征和图像特征，然后训练一个prior 模型根据文本特征生成图像特征，这个图像特征以 CLIP 提取的图像特征为 ground truth，结果再训练一个decoder 模型根据该图像特征还原成原图像。用概率的角度解释其合理性就是.

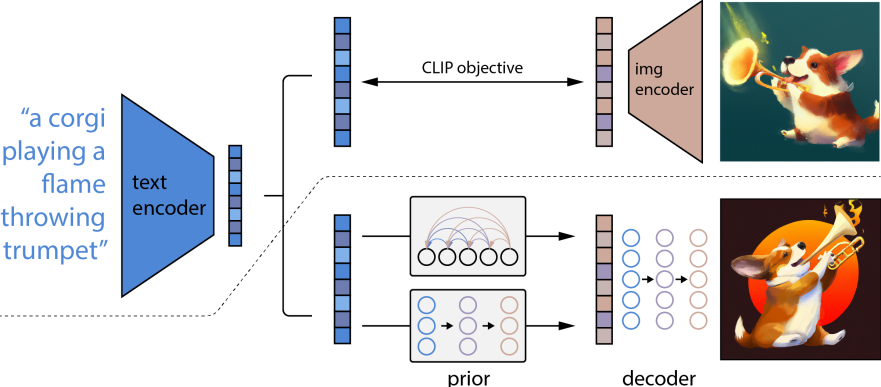
    DALL·E 2整体架构图

    1. Prior

    Prior 模型根据文本特征预测对应的图像特征，技巧大概可以分为两种，一种是自回归预测，用文本特征序列去预测 CLIP 那边的图像特征；另一种是扩散生成，即采用扩散模型来生成图像特征，值得注意的是这里直接预测特征比预测噪声效果要更好。

    2. Decoder

    Decoder 根据 Prior 得到的图像特征生成图像，启用的是扩散模型，并用上了Classifier Free Guidance、级联式生成等技巧。

    六、Flow Matching

    基于ODE的Flow Matching，从SDE角度看扩散模型，以及Classifier-Free Guidance介绍。

    七、Latent Diffusion Model

    Latent Diffusion Model (LDM)，是 Stable Diffusion 的核心，是一种高效的生成模型，它将扩散模型（如 DDPM）的操作从高维像素空间转移到更低维的潜在空间 (Latent Space)，从而大幅减少计算资源和训练/推理时间，同时保持极高的生成质量。

    1. 核心思想与架构

    LDM 巧妙地结合了 VQ-VAE 或 VAE 的编码器-解码器结构与 DDPM 的扩散和去噪过程。

    • 问题：DDPM 直接在像素空间 (如$512 \times 512 \times 3$维) 运行，计算和内存成本极高。

    • 解决方案：使用一个预训练的自编码器（如 VAE）将图像压缩到一个更小的潜在空间$z$，然后在低维空间上执行扩散和去噪。

    LDM 的整体架构由三个主要组件构成：

    组件名称作用模型类型
    感知压缩（Perceptual Compression）

    编码器 $E$: 将高维图像$x$压缩到低维潜在表示$z$.

    解码器 $D$: 将 $z$解码回像素空间$\hat{x}$.

    		VAE/VQ-VAE
    潜在空间扩散(Latent Diffusion)在潜在空间 $\mathbf{z}$上学习去噪，充当扩散模型的参数化逆过程$p_{\theta}(\mathbf{z}_{t-1}\mathbf{z}_t)$U-Net
    条件机制(Conditioning Mechanism)负责将各种条件信息$y$(如文本、类别标签等) 引入到 U-Net 中，指导去噪过程。投影层 + Cross-Attention

    LDM 将高维数据的学习（如图像）分为两个不同的阶段：

    1. 感知压缩阶段：训练一个 VAE/VQ-VAE，达成高效的、感知上等效的压缩和解压缩。

    2. 潜在生成阶段：在低维潜在空间上训练一个扩散模型（U-Net），用于生成和去噪。

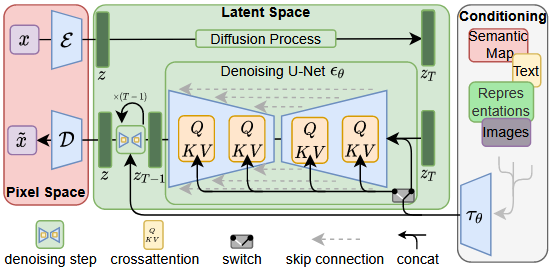
    LDM 架构图

    2. 潜在扩散过程

    1) 编码与压缩

    LDM 首先使用预训练的编码器$E$ 将原始图像 $\mathbf{x} \in \mathbb{R}^{H \times W \times 3}$编码为一个低维的潜在表示$\mathbf{z} \in \mathbb{R}^{h \times w \times c}$.

    其中，$h < H, w < W$通过. 例如，能够将$512 \times 512$ 图像压缩到 $64 \times 64$的潜在空间。

    2) 潜在空间的扩散与去噪

    所有的扩散和去噪操作都在该低维潜在空间$\mathbf{z}$ 上进行。

    • 正向扩散：向潜在变量 $\mathbf{z}$中逐步添加高斯噪声，直到变成纯噪声$\mathbf{z}_T$。

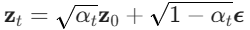
      （其中 $\boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$）

    • 反向去噪：训练一个 U-Net 预测每一步添加的噪声$\boldsymbol{\epsilon}$，以建立去噪。

      损失函数： 与 DDPM 类似，但作用在潜在空间上。

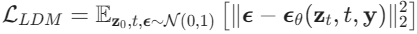
    3) 解码与生成

    在推理时，U-Net 从$\mathbf{z}_T \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$开始去噪，得到最终的去噪潜在变量$\mathbf{z}_0$. 然后使用预训练的解码器$D$将其还原为高分辨率图像$\hat{\mathbf{x}}$.

    3. 条件机制

    LDM 引入了Cross-Attention条件嵌入机制，使其能够将各种模态的条件信息$y$融合到 U-Net 内部然后采用 Classifier-Free Guidance进行条件生成。

    • 编码条件信息：不同的条件（文本、标签、语义图等）首先通过一个领域特定的编码器$\tau_{\phi}$转化为一个特征向量序列$\mathbf{y}$（例如，文本通过 Transformer 编码器）。

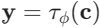
    • 注入 U-Net：在 U-Net 的中间层，依据 Cross-Attention 块将潜在特征$\mathbf{z}_t$ 与条件 $\mathbf{y}$ 连接起来。

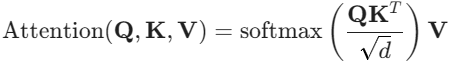
      • $\mathbf{Q}$(Query) ：来自 U-Net 的含噪潜在特征$\mathbf{z}_t$.

      • $\mathbf{K}$(Key) 和$\mathbf{V}$(Value) ： 来自条件特征$\mathbf{y}$.

    八、Diffusion Transformer

    DiT 是一种将 Transformer 架构引入到扩散模型DDPM去噪过程中的创新模型。它将传统的 U-Net 去噪骨干网络替换为一系列Transformer 块，在潜在空间$\mathbf{z}$上执行去噪操作。

    • 核心思想：将图像去噪任务建模为对潜在图像块（Latent Patches）序列的序列到序列（Sequence-to-Sequence）预测任务。

    1. Model Architecture

    DiT 的整体架构遵循 LDM 的范式，即在 VAE/VQ-VAE 压缩后的潜在空间中操作。

    1) 输入处理 (Input Processing)

    • 潜在表示： 原始图像 $\mathbf{x}$开始通过 VAE 编码器$E$压缩为潜在特征$\mathbf{z} \in \mathbb{R}^{h \times w \times c}$.

    • 分块与展平 (Patchify & Flatten)：

      • 将潜在特征 $\mathbf{z}$拆分成一系列不重叠的二维图像块（Patches）。

      • 将这些块展平为一维向量，形成一个序列$\mathbf{z}_{\text{seq}} \in \mathbb{R}^{N \times d}$，其中 $N$是块的数量，$d$是每个块的维度 ($d = \text{patch\_size} \times \text{patch\_size} \times c$).

    • 位置嵌入 (Positional Embedding)：由于 Transformer 缺乏卷积操作的位置归纳偏置，需要添加可学习的位置嵌入到每个块向量中，以保留空间信息。

    • 时间与条件嵌入： 时间步 $t$ 和其他条件 $c$被编码为向量，并通过自适应归一化 (AdaLN)注入到每个 Transformer 块中。

    2) Transformer 骨干网络

    DiT 的去噪模型$\boldsymbol{\epsilon}_{\theta}(\mathbf{z}_t, t, c)$ 由堆叠的 Transformer Encoder Block构成，用于处理潜在块序列$\mathbf{z}_{\text{seq}}$.

    • 输入： 潜在块序列 $\mathbf{z}_{\text{seq}}$.

    • 结构：每个 Transformer 块包含一个多头自注意力 (Multi-Head Self-Attention) 子层和一个 MLP 子层。

    • 归一化与条件注入：在自注意力和 MLP 子层之前，运用AdaLN或其变体 (AdaLN-Zero) 进行归一化和条件注入。

    3) 输出处理 (Output Processing)

    • 逆分块与重塑：Transformer 块的输出序列$\mathbf{z}'_{\text{seq}}$被重新排列并重塑回二维潜在特征$\mathbf{z}' \in \mathbb{R}^{h \times w \times c}$.

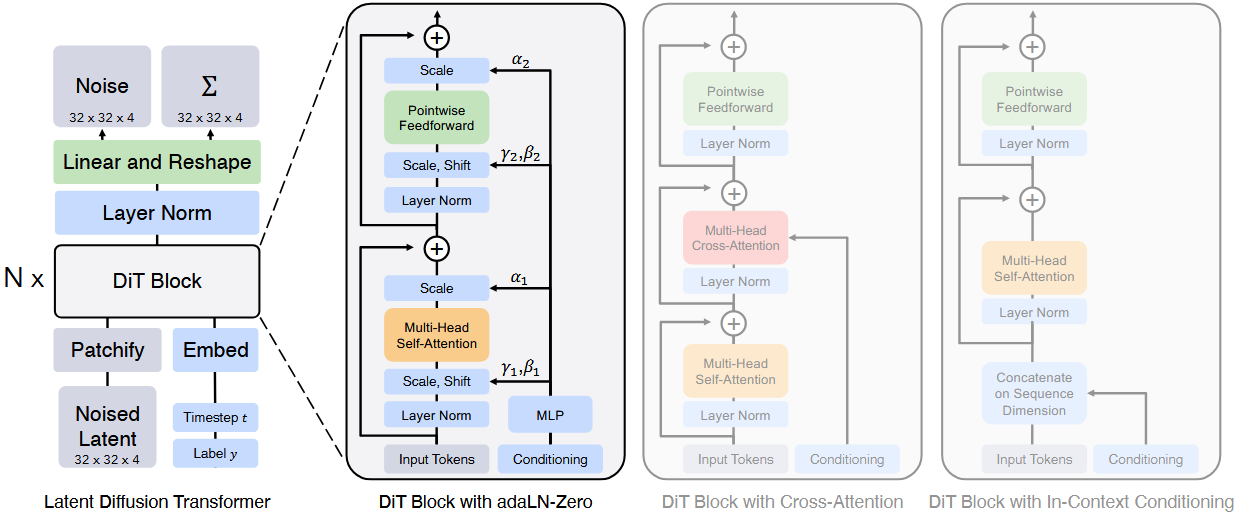
    • 最终预测层：一个最终的线性投影层将$\mathbf{z}'$映射到预测的噪声$\boldsymbol{\epsilon}_{\theta} \in \mathbb{R}^{h \times w \times c}$.

    DiT 架构图

    2. 条件嵌入方式

    作者探索了四种将时间$t$ 和类别 $c$（Conditioning）信息注入到 Transformer 块中的机制，它们在计算效率、灵活性和归一化策略上有所不同。

    1) 语境嵌入 (In-context Conditioning)

    • 机制： 将 $t$ 和 $c$的嵌入向量作为两个额外的 Token，直接拼接到输入的潜在图像块序列中。

    • 处理方式：这两个条件 Token 在 Transformer 块内被视为普通的图像 Token，与其他 Token 一起参与自注意力的计算，从而将条件信息融入整个序列。

    • 输出处理：在经过最后一个 Transformer 块后，这两个条件 Token 会被移除。

    • 计算效率：对模型引入的Gflops可以忽略不计（negligible），因为它只增加了序列长度。

    • 类比： 类似于 ViT 中的 [CLS] Token，用于承载全局信息。

    2) 交叉注意力块 (Cross-Attention Block)

    • 机制： 将 $t$ 和 $c$ 的嵌入向量串联起来，形成一个长度为二的序列，作为单独的条件序列。Transformer 块被修改，在多头自注意力（Multi-Head Self-Attention）之后，增加一个多头交叉注意力 (Multi-Head Cross-Attention)层。

    • 注入方式：图像潜在 Token 序列作为 Query，条件序列作为 Key 和 Value。

    • 计算效率： 引入的 Gflops 最多，约为 15% 的开销（overhead），但提供了最灵活的、基于内容的条件注入。

    • 类比：类似于原始 Transformer 和 LDM 中用于类别标签等条件的注入方式。

    3) 自适应层归一化 (AdaLN) 块

    • 机制：替换 Transformer 块中的标准 Layer Norm 为Adaptive Layer Norm (AdaLN)。

    • 参数回归： AdaLN 不直接学习$\gamma$ 和 $\beta$参数，而是从$t$ 和 $c$ 嵌入向量的和 (sum)中回归 (regress)出维度级的缩放$\gamma$ 和偏移 $\beta$参数，也就是\begin{bmatrix} \gamma(c+t) \\ \beta(c+t) \end{bmatrix} = \operatorname{MLP}(c+t)，从而有y_i = \gamma_i(c+t) \cdot \hat{x}_i + \beta_i(c+t).

    • 计算效率： 引入的 Gflops 最少计算效率最高的条件注入方式。就是，

    • 局限性： 这种机制限制了对所有 Token 应用相同的函数（$\gamma$ 和 $\beta$是全局生成的），这意味着它无法在空间维度上对特征进行精细的条件调整。

    4) AdaLN-Zero 块

    • 机制：对 AdaLN 块的修改，旨在实现残差块的零初始化（Zero-Initialization），使残差块在初始化时表现为恒等函数。

    • 额外参数： 除了回归 $\gamma$ 和 $\beta$之外，还回归一个维度级（dimensionwise）的缩放参数$\alpha$，即\begin{bmatrix} \gamma(c+t) \\ \beta(c+t) \\ \alpha(c+t) \end{bmatrix} = \operatorname{MLP}(c+t).

    • 应用位置：$\alpha$参数被应用在 DiT 块内任何残差连接之前，即.

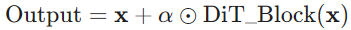    • 目标：在初始化时，依据零初始化$\alpha$（即使预测 $\alpha$的 MLP 输出接近零），使得残差分支的贡献为零，从而加速大规模训练的收敛和稳定性。

    九、LoRA

    LoRA 是一种参数高效的微调（Parameter-Efficient Fine-Tuning, PEFT）方式，旨在解决对超大规模预训练模型进行微调时可能带来的过量训练开销、推理延迟等问题。

    LoRA 的核心假设是：在模型适应 (adaptation) 特定下游任务时，全连接层的权重的更新量 $\Delta W$ 具有低“内在秩” (Low Intrinsic Rank)，因此，更新矩阵$\Delta W$可以用两个低秩矩阵的乘积来近似表示。

    1. 重参数化

    1) 数学原理

    对于预训练模型中的任意一个权重矩阵$W_0 \in \mathbb{R}^{d \times k}$(例如 Transformer 中的$W_q, W_v, W_k, W_o$ 矩阵)：

    • 全量微调： 权重更新为 $W = W_0 + \Delta W$.
    • LoRA： 将更新量 $\Delta W$分解为一个低秩表示$\Delta W = BA$.

    其中：

    • $W_0$ 是预训练权重，在微调过程中被冻结（Frozen），不接收梯度更新。
    • $\Delta W = BA$ 是低秩分解矩阵，$B \in \mathbb{R}^{d \times r}$，$A \in \mathbb{R}^{r \times k}$，秩 $r$是 LoRA 模块的超参数，且$r \ll \min(d, k)$ (通常 $r$可以很小，如 1 或 2，而$d$可能高达 12,288).

    • 只有矩阵 $A$ 和 $B$ 中的参数是可训练的 (Trainable).

    2) 前向传播 (Forward Pass)

    LoRA 模块在计算时是并行进行的：

    其中 $\mathbf{x}$ 是输入，$\mathbf{h}$ 是输出。

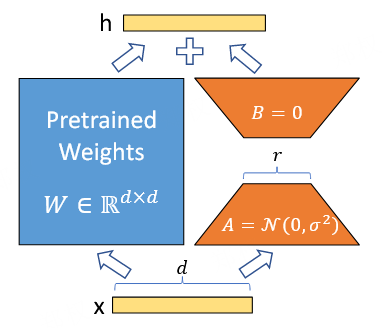
    LoRA示意图

    3) 初始化和缩放

    • 初始化： 矩阵 $A$ 使用随机高斯分布初始化，而矩阵$B$ 初始化为零矩阵。

      • 这样做确保在训练开始时$\Delta W = BA$ 是零矩阵，因此 $\Delta W \mathbf{x}$ 为零。

      • 这实现了零初始化的效果，即训练开始时模型与原始预训练模型的行为相同。

    • 缩放：LoRA 模块的输出$BA \mathbf{x}$会被一个固定的缩放因子$\alpha/r$进行缩放 。

      • $\alpha$是一个常数，通常被设置为试验的第一个$r$ 值。

      • 这个缩放因子有助于减少在改变秩$r$时重新调整学习率等超参数的需求。

    2. 关键优势

    LoRA 在保持模型性能的同时，解决了全量微调的几个主导挑战。

    优势详细说明来源
    极大地减少可训练参数

    相比 GPT-3 175B 的全量微调，LoRA 可以将可训练参数数量减少 10,000 倍。每个下游任务只需要存储和加载小的$A$ 和 $B$ 矩阵。

    		硬件/存储
    减少内存消耗

    通过训练时，由于无需计算冻结参数的梯度或维护优化器状态，LoRA 能够将GPU 内存（VRAM）需求减少多达 3 倍。对于 GPT-3 175B，VRAM 消耗从 1.2TB 减少到 350GB.

    		硬件/存储
    无额外推理延迟

    在部署时，行将$\Delta W = BA$ 显式计算并合并到预训练权重$W_0$中，得到最终的权重$W = W_0 + BA$. 推理时，可以直接使用$W$，不引入任何额外的计算或推理延迟，优于 Adapter 等方法。

    		部署/延迟
    高效任务切换

    在部署环境中，切换到另一个任务只需要减去旧的 $BA$矩阵，然后加上新的$B'A'$ 矩阵，操作高效，内存开销极小。

    		部署/效率
    媲美全量微调的性能

    在 RoBERTa、DeBERTa、GPT-2 和 GPT-3 等模型上，LoRA 的模型质量表现与全量微调相当或更好。

    		模型质量

    3. 应用位置

    理论上，LoRA 可以应用于神经网络中任何稠密层 (Dense Layer，即全连接层)的权重矩阵。在 Transformer 架构中，LoRA 主要应用于自注意力模块：

    • Query 投影矩阵$W_q$

    • Key 投影矩阵$W_k$

    • Value 投影矩阵$W_v$

    • Output 投影矩阵$W_o$

    在 DiT 论文的实验中，作者通常仅将 LoRA 应用于$W_q$ 和 $W_v$，以达到简化和参数效率的目的。实验证明，仅对$W_q$ 和 $W_v$进行适应通常能达到最佳的综合性能。

    posted @ 2025-12-22 13:53  clnchanpin  阅读(29)  评论(0)    收藏  举报