深入解析:傅里叶分析体系的理解
目录
前言
傅里叶分析实际是信号合成与分解的一种方式,正变换是将时域的信号分解到频域的各个频率上面,逆变换就是将频域上的各个频点的幅值合成时域的信号。常用的有两种类型的分解,一种是三角函数集,这是单边谱,另一种是复指数集,这是双边谱。借用大佬的图,很直观地看到这种分解与合成的关系。
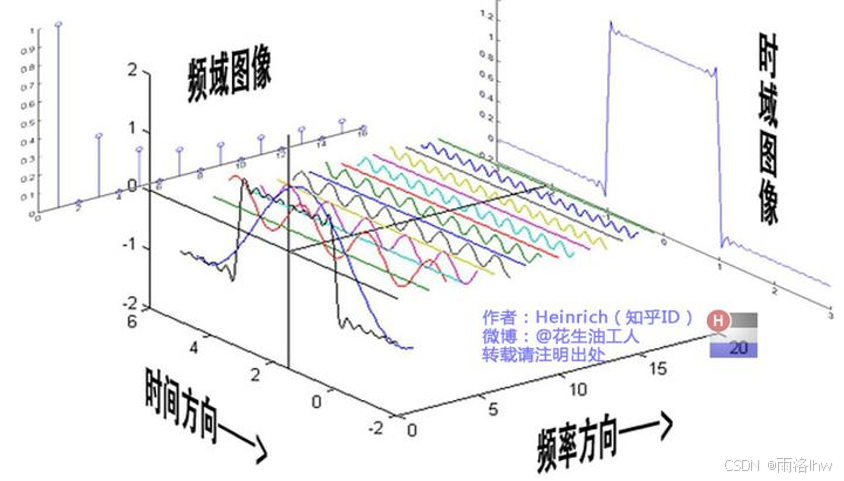
1.傅里叶分析的基础
1.1函数的正交
在数学中,假设两个函数内积为零,则这两个函数 f(x) 和 g(x)称为正交的。
内积公式如下:
,
函数 f(x) 和 g(x)在区间 [t0,t1]上是正交的。
1.2三角函数集的正交性
三角函数集{1, cosx, sinx, cos2x, sin2x, …, cosnx, sinnx}内的函数在区间[-π, π]上彼此正交,即其中任意两个不同的函数在区间[-π, π]上的内积为0。证明如下:
要证明对于任意两个不同的函数 f(x) 和 g(x),它们的内积在区间 [−π,π] 上为零,即:
首先证明常数函数和正弦余弦函数的内积为零:
对于常数函数 f(x)=1和任意的正弦余弦函数 g(x)=cos(kx)或 g(x)=sin(kx),其内积为
通过这能够由g(x)的图像得到,因为当时,最大周期是
,
,内积区间刚好在一个周期内,图像面积累加刚好为0,当k为其他值时,
是g(x)周期的整数倍,因而图像面积累加之和还是0。
然后再证明正弦函数和余弦函数不同函数之间的内积为零,相同不为0:
对于任意的 m,n∈Z,有
当m=n时
,对于任何
成立。
所以有:
同理可证:
综上所述,对于任意 m,n∈Z,不同的函数 f(x)和 g(x)的内积都为零,证明了在区间 [−π,π]上,三角函数集是正交的。
有了三角函数集的正交性,就可以理解周期信号傅里叶级数了,将信号投影到每一个正交基上。
1.3复指数函数的正交性
复指数函数集
中的函数在区间上彼此正交,即集合中任意两个不同的函数在该区间上的内积为零。
证明如下:
设:
定义内积为:
这里应该注意的是复数内积应该其中一个改变符号,正改负,负改正。所以会有复数本身的内积等于该复数与其共轭复数相乘。
当 时,有:
利用欧拉公式,可得:
因为 ,则有:
因此:
即不同的复指数函数在区间上正交。
相同的函数内积不为 0
当 时,有:
因此:
所以有集合中任意两个不同的函数在该区间上的内积为零。
同时需要记住函数的内积是在区间内积分的形式。
2.傅里叶分析的类型
傅里叶分析主要根据信号的时域特性(连续/离散、周期/非周期)分为四种基本类型:
- 连续周期信号 → 傅里叶级数 (FS):将周期信号分解为离散频率的指数函数之和。
- 连续非周期信号 → 傅里叶变换 (FT):得到连续谱,揭示信号的频率密度分布。
- 离散周期信号 → 离散傅里叶级数 (DFS)离散且周期的。就是:在频域上也
- 离散非周期信号 → 离散时间傅里叶变换 (DTFT):得到以2π为周期的连续频谱。
2.1连续周期信号 → 傅里叶级数 (FS)
周期信号f(t) ,其周期为T(模拟频率为,也称为基频),当满足狄里赫利条件(能量有限且绝对可积)时,它可以分解为如下三 角级数,该三角级数称为傅里叶级数。
信号在对应频率的基上的坐标,代表该频率的分量的强度。就是其几何意义是周期信号行投影到三角函数正交基上,其系数
一般形式:
其中,
,
,
一样的)就是。(这里积分上下限之所以是一个周期,是因为该信号是周期函数,只需要考虑一个周期内的变化即可,其他区间
这里的系数就是由投影到各个频率的三角函数上得到的,以
为例子:
利用辅助角公式:
可以将上面的形式进一步化简:
单边谱,就是这样子表示的是幅度谱,
是相位。
可能转换为复指数形式,这样子信号就分解在复指数上面了,即投影在复指数上面。利用公式:
转换为:
其中,负频率代表旋转方向,相位部分移到了,
这样子就可以将余弦信号的单边谱,变为复指数形式的双边谱。双边谱具有幅度谱偶对称,幅值减半;相位谱奇对称的特点。其中,就是在该复指数上的投影值。
2.2连续非周期信号 → 傅里叶变换 (FT)
正变换的推导:
非周期信号可以理解为周期为无穷大的周期信号。根据傅里叶级数,周期信号可以投影到不同频率的分量:
其中,是基本频率。当周期
时,基本频率
,此时
也会趋向于 0,傅里叶级数的频率分量
趋于连续频率
。但是这样子的话
对应的值将趋于 0,表示在这些低频区域信号的贡献逐渐消失,意味着没有实际的意义。
因而会定义了频谱密度:
逆变换的推导:
通过同理,将非周期信号理解为周期为无穷大的周期信号。根据傅里叶级数,周期信号能够写成不同频率分量线性组合的形式:
当 时,
,此时,
可以写成
(离散的自变量变为连续),
可以写成
,累加运算变为积分。
因此,连续时间非周期信号许可写成:
这是非周期信号的傅里叶逆变换。
所以傅里叶变换公式如下:
正变换:,将信号分解到整个连续的频域上
逆变换:,对整个频域的信息进行重组恢复出原信号
频率分量上的投影,复数内积的符号变负,所以是就是上面两个公式只需要记住他的意义就很容易记住这两个公式。正变换,但是因为直接投影太小了,没意义,所以
会多乘一个
变成了频谱密度,这样就和
公式的
抵消,变成现在的样子。逆变换是投影分量乘以复指数分量,而
和
是有公式推导出来的,因为是连续谱,故而是积分形式。
常用性质
在实际数字处理中常用到以下这些性质:
(1)时间与频率的尺度变换
若,则有 :
其中,为时间的缩放因子。当
时,信号在时间轴上被压缩,信号的频率变大,频率上被拉伸;当
时,信号在时间轴上被拉伸,信号频率变小,频率上被压缩。
(2)时移性质
若,则有 :
信号在时间上的移位,并不改变它的傅里叶变换的模长,即不会影响原来的频率分量,只是在变换中引入相移,且相移 与频率成线性关系,对于频率越高的分量,移位越多。这个性质说明了信号延迟和信号提前都不会改变频率的幅度,只会改变频率的相位。
(3)卷积性质
若:,
, 则:
(4)乘法性质
若:,
, 则:
时域上的乘法对应频域上的卷积,该性质是信号调制的基础。
举个例子,波长,发射信号的天线尺寸与信号波长成正比,波长越大,天线尺寸越大 减小天线尺寸,需要提高信号频率,将低频信号调制到高频,再发送。高频信号也称载波信号。调制信号公式如下:
除了信号调制之后,常用的加窗也是这个性质。
2.3离散周期信号 → 离散傅里叶级数 (DFS)
定义:对于离散时间周期信号,其周期为
(数字角频率为
通过),根据傅里叶级数的原理,信号能够表示为一系列离散时间单位圆上复指数信号的线性组合,即:
其中, 是复指数信号的系数,其表达式为:
,
是数字角频率,
是周期,n是节拍,并且
只涵盖一个周期。实际上,起点并不一定是零,只要能够涵盖一个周期即可,例如:
的范围可以是
,这是因为对于信号
,其周期性保证了
的选择在一个周期内是等效的。
因为,所以
当=0~
时,
是由0~
的;
当时,
=
,而且
,
离散的,周期的。就是是周期性的,所以离散周期信号的频率谱
2025-11-24-lhw:补充从连续到离散的过程
根据奈奎斯特采样定理(Nyquist-Shannon Sampling Theorem),为了从连续傅里叶变换(CFT)获得离散傅里叶变换(DFT),采样频率必须至少为信号频率的两倍,即:
其中 是信号的最高频率。
在这种条件下,离散傅里叶变换就是对连续傅里叶变换
在离散频率点的近似。具体地,离散频率
是:
这意味着将连续信号的频域上每个频率间隔离散化为
个点,形成一个周期性的频谱。而周期的范围是
,即整个频率带宽是fs,所以会有基波频率
。基波频率,也叫频率分辨率的概念,就是如果大家按照
的采样频率去采集一个信号,一 共采集 N 个点,那么基波频率(频率分辨率)就是
。这样,第 n 个点对应信号频率为:
; 其中 n≥1,当 n=1 时为直流分量。(需要注意的是频率是不应该考虑
的,角频率
才需要考虑,
)
2.4离散非周期信号 → 离散时间傅里叶变换 (DTFT)
推导的方式和连续非周期信号的相似。
DTFT的本质:能量有限或绝对可和的离散时间非周期信号能够分解到覆盖范围为 0, 2的连续频域的单位圆复指数序列上。
正变换推导:
将离散时间非周期信号看作周期为的周期信号。根据离散时间傅里叶级数,周期信号能够投影到
个不同频率的分量上:
当 时,
,此时,
可以写成
(频域变得连续)。然而,
,这表示傅里叶级数的结果在这里没有明确的物理意义。
同样地,能够定义频谱密度:
对于离散时间非周期信号的傅里叶变换,变换结果通常是周期性的,周期为。根本原因是
,当
取大于
时,会重复
。
离散傅里叶变换(DFT)将信号投影到一个周期性的频率轴上,而周期性是由离散时间信号的周期性所固有的。究其原因,傅里叶变换的周期性特性来自于离散信号的周期性,导致频域上变得周期化。傅里叶级数在连续信号中对应于一个周期性的频域,而在离散信号中,该频域成为了一个周期为的离散频域。
逆变换的推导:
通过同理,将非周期信号理解为周期为无穷大的周期信号。根据离散傅里叶级数,周期信号能够写成不同频率分量线性组合的形式:
当 时,
,此时,
可以写成
(离散的自变量变为连续),
可以写成
,累加运算变为积分。
因此,离散时间非周期信号可以写成:
非周期信号的傅里叶逆变换。就是这
所以对于离散信号来说,频谱上是周期延拓的,只需要对一个周期内的频域线性组合即可。需要注意的是离散时间矩形信号频谱密度:
- [0,2]为基本周期延拓;
- 也可[-,]为根本周期延拓;
- 0,2附近为低频分量;
- -,附近为高频分量
常用的性质
(1)周期性
(2)卷积性质
若:,
, 则:
(3)乘法性质
若:,
, 则:
3.快速傅里叶变换(FFT)
3.1 FFT的来源
数字信号,所以无法进行连续时间的傅里叶变换;就是传感器的信号离散时间傅里叶变换针对长度为无穷长的信号,其得到的频谱是连续的,与实际信号的情况也不一致; 离散时间傅里叶级数针对离散的信号,频谱的结果也是离散的,最有可能由计算机实现,但其针对周期信号。 实际上,计算机采用“离散傅里叶变换(DFT)”对信号开展分析—基本原理:将采集到的信号(信号长度为看成周期为
的离散时间周期信号,并计算其DTFS。
所以有离散傅里叶变换(DFT)的出现:对于长度为的信号
,将其看成周期为
的周期信号(这种合理,结果会有误差,但不影响分析就是做法),其公式为:
正变换:
逆变换:
DFT的计算量:N个点直接计算DFT的总运算量为:次复数乘法,
次复数加法。分析1024个点的序列,需要进行百万次的复乘,消耗的资源比较多。

3.2 基2-FFT的蝶形运算
给定长度为 的离散序列
,其离散傅里叶变换(DFT)定义为:
引入旋转因子,定义为:
,所以
将原始序列分解为偶数子序列和奇数子序列:
然后利用的可约性:
如果将原来的数据分为两组运算就会变成这样子的:
(用的也是可约性)
其中: 是由
构成的偶数索引子序列的 DFT;
是由
构成的奇数索引子序列的 DFT;
用AI举个例子:



从这个例子也可能看出FFT的运算原理:
递归分解:大DFT不断拆分成小DFT,直到最主要的2点DFT(只分然而先不进行运算,知道2点再往回运算)
奇偶分组:每次分解都按照序列索引的奇偶性进行分组
蝶形组合:分解后的小DFT结果通过蝶形运算(加减和旋转因子乘法)组合成大的DFT结果
计算复杂度:直接从O(N²)降到O(N log₂N)
一般用蝶形图表示,如下:

只是该图对于初学者可能会有点误导,理解的话还是按AI给出的例子的流程来理解。
通过然后从中也能够看出和
可以用一组蝶形运算来计算。
基数-2蝶形运算表示一对输入和
,其输出为:
只应该一次复数乘法,两次复数加法(这两次加法一次实现为“加”,另一次实现为“减”)
因为实际的数字信号处理中我们会直接采用库函数计算,所以就不记录实际的计算过程了。FFT是分析频域信息常用的技巧。
4.短时傅里叶变换(STFT)
传统FFT作为一种全局变换,其频谱结果不包含时域信息,这导致时域上不同的信号(如具有相同频率成分但出现时刻不同的信号)可能产生相同的频谱图,从而丢失了信号的时间局部化特征。
为克服此问题,短时傅里叶变换通过对信号进行加窗分段,并对每一段信号分别进行FFT分析。这种方法将一维的时域信号映射为一个二维的时频分布,从而能够清晰地揭示信号频率成分随时间的变化情况。
具体行参考这篇文章:时频分析之STFT:时频分析之STFT:短时傅里叶变换的原理与代码实现(非调用Matlab API)-CSDN博客
这里借用一下他的图:
两种不同的信号,做FFT之后频谱图是一样的。
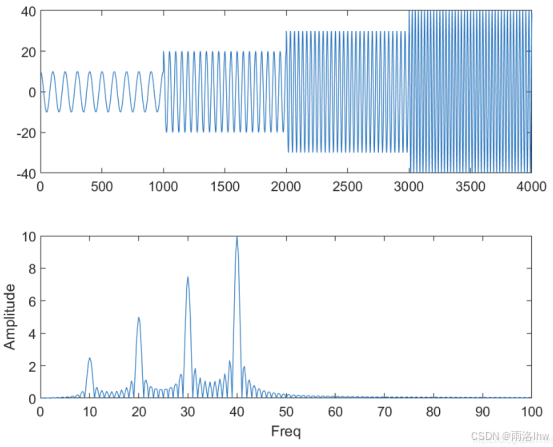
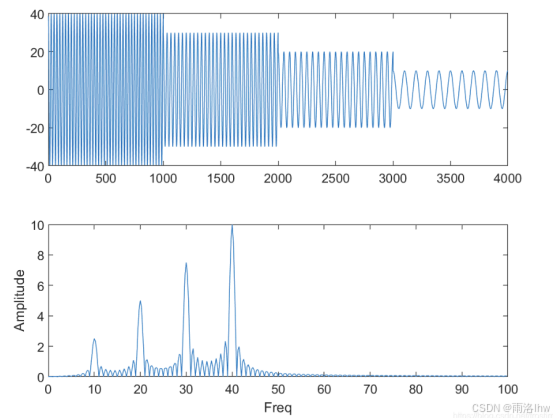
但是如果做短时傅里叶变换的话,是能够看出区别的:
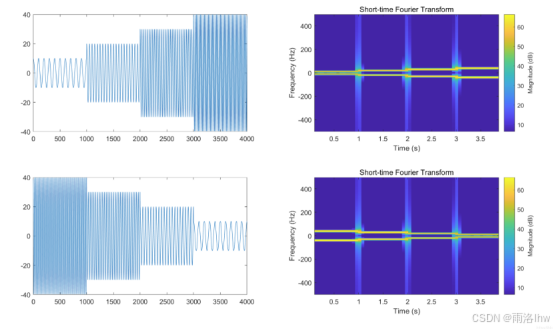
因此,再处理语音等信号时,往往做的是短时傅里叶变换(STFT)。
5.参考资料
时频分析之STFT:短时傅里叶变换的原理与代码实现(非调用Matlab API)-CSDN博客
数字信号处理9-2_连续时间周期信号的傅里叶级数_哔哩哔哩_bilibili
以上就是本次笔记的记录,方便后期的复习与应用。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号