详细介绍：图论专题(十四)：“双重边界”的交汇——逆流而上解「太平洋大西洋水流问题」

哈喽各位，我是前端小L。

欢迎来到大家的图论专题第十四篇！在之前的题目中，我们关注的往往是“是否连通”。今天，我们要处理的是一种具有方向性的连通——水流。

水往低处流。倘若我们要判断每一个格子上的雨水能否流向大海，最直观的做法是模拟每个格子的水流路径。但这会产生大量的重复计算。正如我们在 LC 130 中学到的：与其模拟水怎么“流下去”，不如思考大海怎么“逆流上来”！

力扣 417. 太平洋大西洋水流障碍

https://leetcode.cn/problems/pacific-atlantic-water-flow/

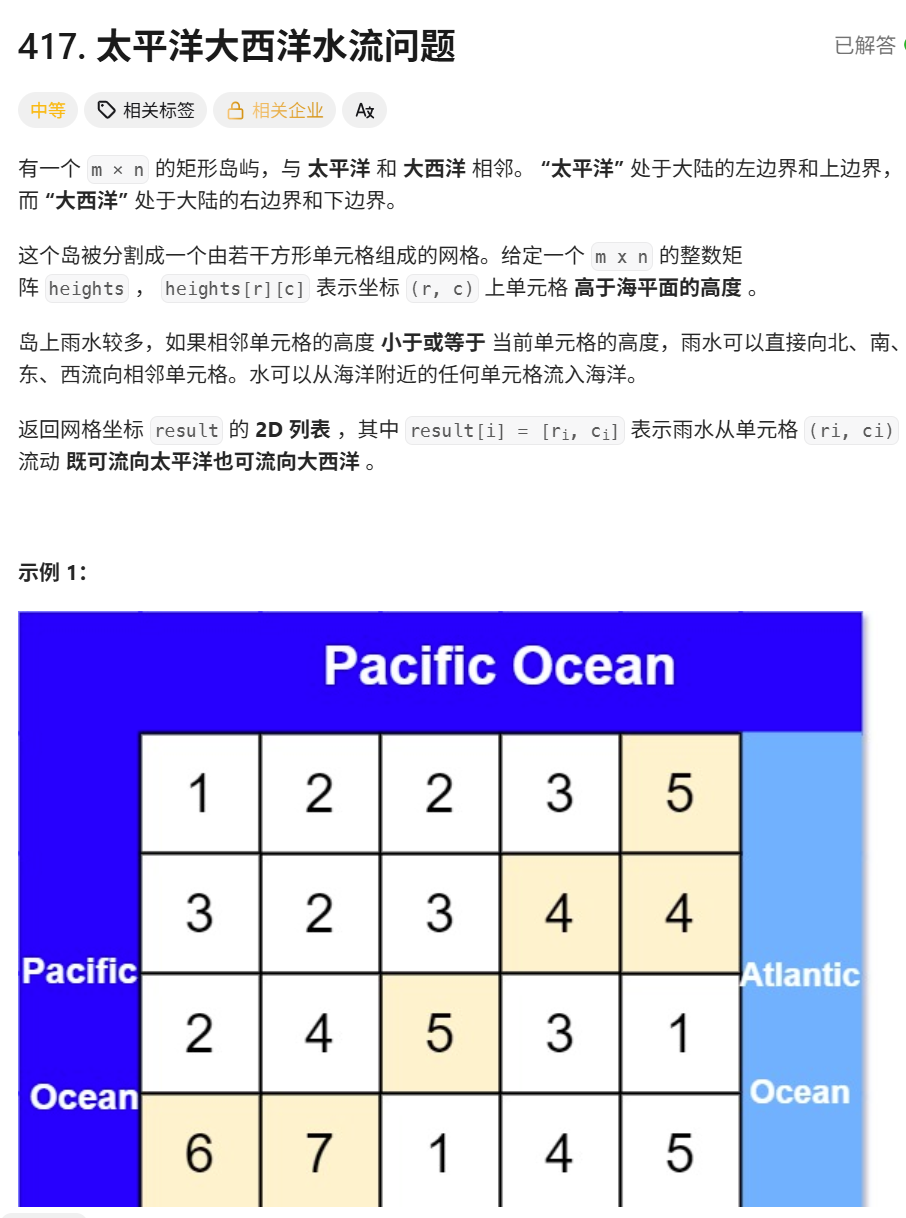
题目分析：

• 输入：一个 m x n 的非负整数矩阵 heights，代表海拔高度。

• 地理位置：

  • 太平洋：接触矩阵的左边界和上边界。

  • 大西洋：接触矩阵的右边界和下边界。

• 流向规则：水只能从高处流向低处（或等高）。即 heights[当前] >= heights[邻居]。

• 目标：找出那些水既能流向太平洋，又能流向大西洋的单元格坐标。

例子：一个“山脊”上的点，它的水可能向左流进太平洋，向右流进大西洋。我们要求找到这条“分水岭”上的所有点。

思路：“逆向思维”——海水倒灌

如果我们对每个格子都做一次 DFS/BFS 看它流向哪，复杂度极高。 我们沿用 LC 130 的思路：从边界出发！

1. 正向思维（难）：点 A 的水能流到海洋吗？（条件：H_A >= H_next）

2. 逆向思维（易）：海洋里的水，能“逆流”爬到点 A 吗？（条件：H_next >= H_A）

如果大家行找出：

• 集合 P：所有太平洋的水能“爬”到的点。

• 集合 A：所有大西洋的水能“爬”到的点。 那么，既在 P 又在 A 中的点（即 P 和 A 的交集我们要找的答案！就是），就

算法流程：

1. 初始化：

   • canReachP[m][n]：布尔矩阵，记录能流向太平洋的点。

   • canReachA[m][n]：布尔矩阵，记录能流向大西洋的点。

2. 启动 DFS (或 BFS)：

   • 第一轮（太平洋）：遍历左边界和上边界的所有点，作为起点，启动 DFS。标记 canReachP。

     • 逆流规则：只有当 heights[邻居] >= heights[当前] 时，才能爬上去。

   • 第二轮（大西洋）：遍历右边界和下边界的所有点，作为起点，启动 DFS。标记 canReachA。

3. 取交集：

   • 遍历整个网格。

   • if (canReachP[r][c] && canReachA[r][c])：加入结果列表。

4. 返回结果。

代码建立 (DFS)

C++

#include 
using namespace std;
class Solution {
private:
    int m, n;
    // 方向数组
    int dr[4] = {0, 0, 1, -1};
    int dc[4] = {1, -1, 0, 0};
    // DFS 函数：逆流而上
    // visited: 记录当前海洋能到达的点
    void dfs(vector>& heights, vector>& visited, int r, int c) {
        // 标记当前点可达
        visited[r][c] = true;
        // 探索四个方向
        for (int i = 0; i < 4; ++i) {
            int nr = r + dr[i];
            int nc = c + dc[i];
            // 1. 检查越界
            // 2. 检查是否已访问
            // 3. 检查高度：必须是“逆流”，即 新高度 >= 旧高度
            if (nr >= 0 && nr < m && nc >= 0 && nc < n &&
                !visited[nr][nc] &&
                heights[nr][nc] >= heights[r][c]) {
                dfs(heights, visited, nr, nc);
            }
        }
    }
public:
    vector> pacificAtlantic(vector>& heights) {
        if (heights.empty() || heights[0].empty()) return {};
        m = heights.size();
        n = heights[0].size();
        vector> canReachP(m, vector(n, false));
        vector> canReachA(m, vector(n, false));
        // 1. 从 左边界 和 右边界 出发
        for (int r = 0; r < m; ++r) {
            dfs(heights, canReachP, r, 0);      // 太平洋 (左)
            dfs(heights, canReachA, r, n - 1);  // 大西洋 (右)
        }
        // 2. 从 上边界 和 下边界 出发
        for (int c = 0; c < n; ++c) {
            dfs(heights, canReachP, 0, c);      // 太平洋 (上)
            dfs(heights, canReachA, m - 1, c);  // 大西洋 (下)
        }
        // 3. 取交集
        vector> result;
        for (int r = 0; r < m; ++r) {
            for (int c = 0; c < n; ++c) {
                if (canReachP[r][c] && canReachA[r][c]) {
                    result.push_back({r, c});
                }
            }
        }
        return result;
    }
};

深度复杂度分析

• 时间复杂度 O(m * n)：

  • 我们进行了两轮完整的 DFS 遍历（一次为太平洋，一次为大西洋）。

  • 在每一轮中，每个单元格最多被访问一次。

  • 取交集遍历一次网格。

  • 总时间复杂度是线性的 O(m * n)。

• 空间复杂度 O(m * n)：

  • 我们使用了两个 m x n 的布尔矩阵 canReachP 和 canReachA。

  • DFS 的递归栈深度最大为 m * n。

总结

对“就是今天这道题，边界逆向思维”的完美升华。

• LC 130 (被围绕的区域)：我们必须区分“是”与“否”（是否连接边界）。我们只需要一次边界扩散。

• LC 417 (本题)：大家需要区分“A”与“B”（连接哪个边界）。我们进行了两次边界扩散，然后求交集。

此种**“分解问题 -> 分别求解 -> 组合结果”的策略，配合解决麻烦连通性问题的高阶技巧。就是“从结果（海洋）推导原因（陆地）”**的逆向思维，

在下一篇中，大家将面对“网格BFS”的终极 Boss ——带状态的 BFS。当我们在网格中移动时，如果不只是看坐标 (r, c)，还要考虑“手头有多少消除障碍的机会”，BFS 该如何进化？

下期见！