完整教程:三轴机械臂的逆解全流程
介绍:
本文关于三轴机械臂的逆解计算只用到了高中的三角函数,所以对于还没学线代或者刚入门机械臂的小白来说十分友好,可为以后六轴机械臂的逆解计算打基础,文中还用到了很多插图来帮助读者理解,并且提供了相关代码帮助读者将知识加以应用
机械臂结构定义:
L1:大臂长度(J1到J2的距离)L2:小臂长度(J2到J3的距离)目标坐标(
X,Y,Z):机械臂末端(J3)要到达的位置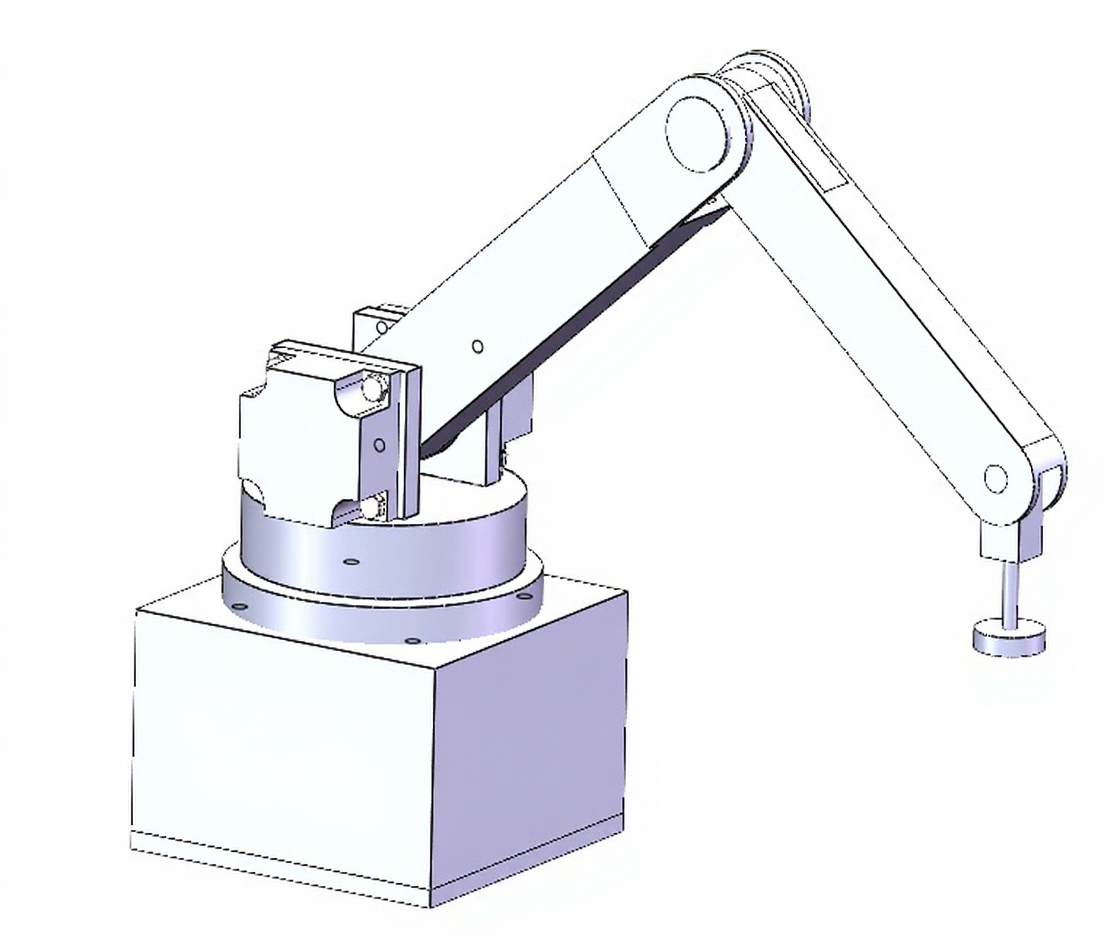
建立坐标系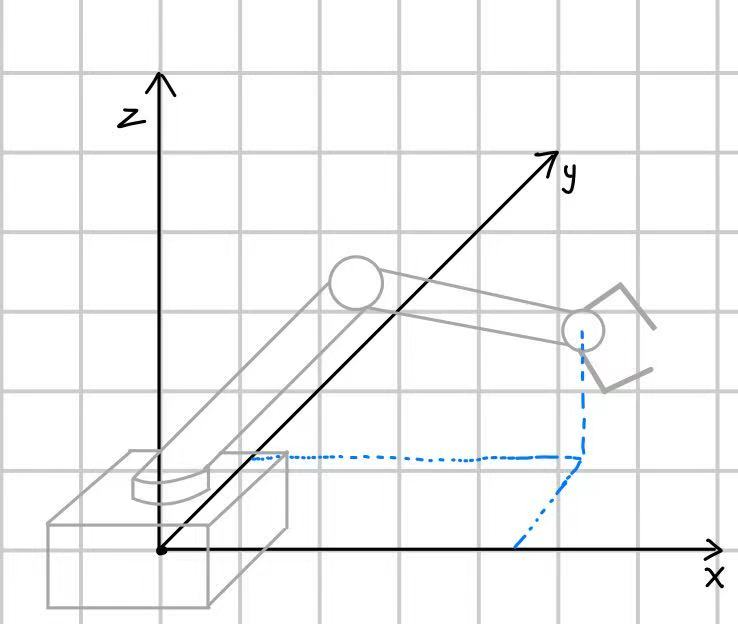
简图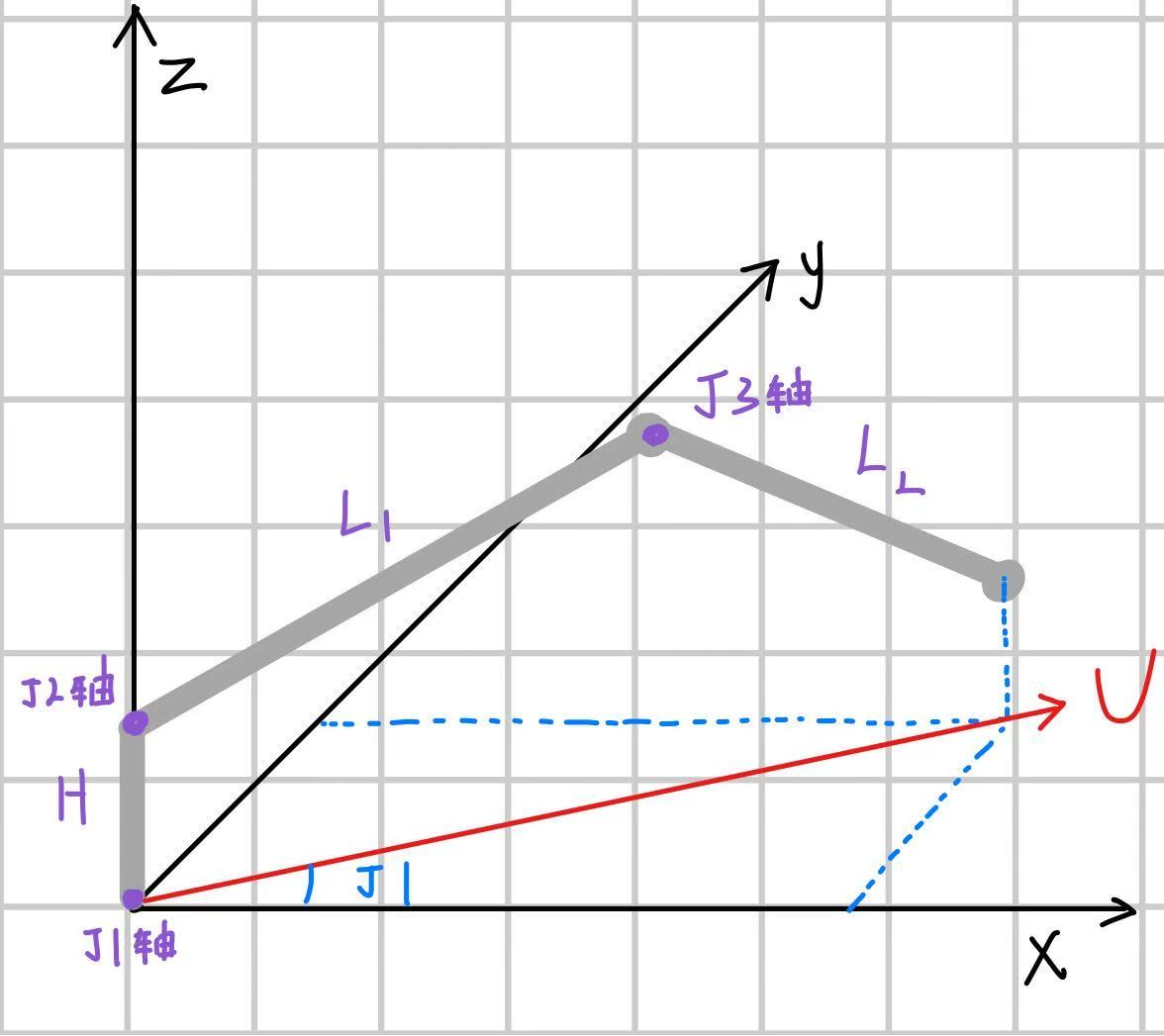
逆解算公式推导(高中数学可懂)
逆解算就是“已知目标坐标,求J1,J2,J3的角度”
关节角度基准(所有关节角度为 0°)

- J1(底盘旋转关节):0° 时,机械臂的 “大臂 - 小臂” 整体沿 基座坐标系 X 轴正方向(即水平向前),无左右旋转。
- J2(大臂摆动关节):0° 时,大臂(J1-J2 段)与 基座坐标系 X 轴完全重合,无上下摆动。
- J3(小臂摆动关节):0° 时,小臂(J2-J3 段)与 大臂(J1-J2 段)完全共线,且沿 X 轴正方向延伸。
求J1(底盘旋转角)
立体图
俯视图
J1控制末端在XY平面的旋转,用反正切函数即可求解:J1 =arctan2(Y/X)
计算出J1 ∈ (-π, π](arctan2 ()默认结果),先转换为0°~360°范围(负角加 360°)
【arctan2()和arctan()的区别:】
arctan():可计算Y/X的反正切值,但无法分辨(1,1)和(-1,-1)这类符号相同但象限相反的点(结果范围:(-π/2, π/2))
arctan2():可判断坐标所在象限,如:X=-1,Y=-1,先明确该点在坐标系的第四象限,再结合Y/X的绝对值计算角度,并且可以解决X=0的情况(结果范围:(-π, π])
求J2(大臂摆动角)

分类讨论:(计算过程类似,这里只详解一种)
H>Z

参数定义:
l1:J2轴的 Z 坐标与目标点 Z 坐标的 差值,l1 = Z - H(若为负数,则目标点在J2的下方)l2:目标点在 XY 平面的投影到原点的距离(即水平距离),l2 = √(X² + Y²)l3:J2轴到目标点的 直线距离(即三角形的斜边),l3 = √(l2² + l1²)θ1:大臂L1与J2轴到末端的连线l3的夹角θ2:l₃与垂直方向(Z 轴)的夹角求解过程:
利用余弦定理求出
cosθ1大小,再利用反正切和反余弦求出θ1和θ2的大小θ1 = arccos( (L1²+l3²-L2²) / (2·L1·l3) )θ2 = arctan2(l2,|l1|)最后
θ1+θ2相加得到J2+90°J2=θ1+θ2-90°
H<Z
计算逻辑与H>Z相同,J2=θ1+θ2-90°
H=Z
l1=0,l3=l2θ2=arctan2(l2, 0)=90°(因|l1|=0),θ1是大臂L1 与J2轴到末端的连线l3 的夹角(因 l3=l2,故等价于大臂与水平方向的夹角)J2=θ1+θ2-90°=θ1

求J3(小臂摆动角)

J3 = 180° - arccos( (L1² + L2² - l3²)/(2·L1·L2) )(余弦定理求的是J3的补角)
细节处理:
1. 判断解的存在性
- 根据
L1和L2的长度计算目标点X,Y坐标范围
若l3 > L1+L2或l3 < |L1-L2|(XY 平面投影超出连杆可达范围),无逆解。 - 根据
J2,J3的限位计算目标点Z坐标范围
若 J2 有向下限位(如 J2≥-θ,θ 为向下最大角度):
Z_max = H + L1 + L2(大臂向上、小臂向上共线)
Z_min = H - L1・sinθ - L2(大臂向下到限位、小臂向下伸直)
若 J2 无向下限位(J2≥-90°):
Z_max = H + L1 + L2
Z_min = H - (L1 + L2)(与原公式一致)
若Z < Z_min或Z > Z_max(Z 轴高度超出可达范围),无逆解
2.处理限位范围问题
| 关节 | 常见限位范围 | 限位原因 | 处理规则 |
|---|---|---|---|
J1 | ±170°(或 0°~340°) | 防止底盘线缆缠绕(如动力线、信号线) | 特殊场景:若需连续旋转,可通过 “多圈计数” 优化 |
J2 | -30°~90°(或 0°~90°) | 1. 向下摆动超-30°(低于水平),大臂可能与底盘底座干涉;2. 向上摆动超 90°(垂直向上),大臂与小臂易发生连杆碰撞 | 若你的机械臂J2无向下摆动需求,可直接限定J2 ∈ [0°, 90°] |
J3 | 0°~180° | 1. 小臂向后翻折(J3 < 0°)会与大臂干涉;2. 小臂顺时针旋转超 180°,小臂会折叠到自身极限 | J3的限位是 “避免小臂与大臂干涉”,需与J2角度联动检查 |
逆解计算流程总结
- 输入参数:
L1(大臂长)、L2(小臂长)、H(J2 的 Z 高度)、目标坐标(X,Y,Z) - 计算
J1:J1 = arctan2(Y, X)(转换为角度,范围[-180°, 180°]); - 计算辅助参数:
l2=√(X²+Y²),l1=Z-H,l3=√(l2²+l1²); - 判断解的存在性:若目标点坐标不在机械臂可到达范围输出 “无逆解”,结束;
- 计算 J2:
- 计算
θ1=arccos( (L1²+l3²-L2²)/(2·L1·l3) )(范围[0°, 180°]) - 计算
θ2=arctan2(l2, |l1|)(范围[0°, 90°]) - 利用通式
J2=θ1+θ2-90°,计算J2
- 计算
- 计算
J3:J3 = 180° - arccos( (L1² + L2² - l3²)/(2·L1·L2) ); - 限位检查:若
J2、J3超出机械臂物理限位,输出 “角度超限位”,否则输出(J1, J2, J3)。
完整的逆解计算示例
1.输入已知参数
| 参数类型 | 具体数值 | 备注 |
|---|---|---|
| 机械臂结构参数 | L1=500mm(大臂长度) | J1 到 J2 的距离 |
| L2=300mm(小臂长度) | J2 到 J3(末端)的距离 | |
| H=100mm(J2 关节的 Z 高度) | J2 固定在基座上方 100mm 处,Z 坐标恒为 100mm | |
| 目标坐标 | (X=400mm, Y=0mm, Z=400mm) | 末端需到达的位置(Y=0 表示在 X 轴正方向) |
| 关节限位 | J1∈[0°, 340°],J2∈[-30°, 90°],J3∈[0°, 180°] | 常见桌面级机械臂限位 |
2.计算 J1(底盘旋转角)
- 公式:
J1 = arctan2(Y, X) - 代入数值:
J1 = arctan2(0, 400) = 0°(Y=0,X>0,对应 X 轴正方向) - 范围转换:因结果 0°∈[0°, 360°],无需调整,最终J1=0°
3.计算辅助参数(l1、l2、l3)
l1 = Z - H
代入数值:l1 = 400 - 100 = 300mm(l1>0,说明末端在 J2 上方,对应 H<Z 场景)l2 = √(X² + Y²)
代入数值:l2 = √(400² + 0²) = 400mml3 = √(l2² + l1²)
代入数值:l3 = √(400² + 300²) = √(160000 + 90000) = √250000 = 500mm- 汇总:
l2=400mm,l1=300mm,l3=500mm
4.判断解的存在性(避免无效计算)
需同时满足 “XY 平面可达” 和 “Z 轴可达” 两个条件,否则无逆解XY 平面可达性(三角形边长关系)
条件:`|L1 - L2| ≤ l3 ≤ L1 + L2` 最小值:`|500 - 300| = 200mm` 最大值:`500 + 300 = 800mm` 当前 l3=500mm,满足 200mm≤500mm≤800mm,**XY 平面可达**Z 轴可达性(结合 J2 限位)
已知 J2 有向下限位 θ=30°(J2≥-30°),需计算 Z_min 和 Z_max: 最大高度 Z_max:`H + L1 + L2`(大臂 + 小臂共线向上) 代入:`Z_max = 100 + 500 + 300 = 900mm` 最小高度 Z_min:`H - L1·sinθ - L2`(大臂向下到限位,小臂向下伸直) 代入:`Z_min = 100 - 500×sin30° - 300 = 100 - 500×0.5 - 300 = 100 - 250 - 300 = -450mm` 当前 Z=400mm,满足 - 450mm≤400mm≤900mm,**Z 轴可达**结论:目标点在机械臂工作空间内,有逆解,可继续计算
5.计算 J2(大臂摆动角)
求 θ1(范围 [0°, 180°])
公式:θ1 = arccos( (L1² + l3² - L2²) / (2·L1·l3) )
代入数值:
分子:500² + 500² - 300² = 250000 + 250000 - 90000 = 410000
分母:2×500×500 = 500000
比值:410000 / 500000 = 0.82
查反余弦表 / 计算器:θ1 = arccos(0.82) ≈ 34.9°求 θ2(范围 [0°, 90°])
公式:θ2 = arctan2(l2, |l1|)(|l1|=300mm,因 l1>0)
代入数值:θ2 = arctan2(400, 300) ≈ 53.13°(直角三角形对边 400、邻边 300,tanθ=4/3,对应角度≈53.13°)求 J2(通式)
公式:J2 = θ1 + θ2 - 90°
代入数值:J2 = 34.9° + 53.13° - 90° ≈ -1.97°
6.计算 J3(小臂摆动角)
- 公式:
J3 = 180° - arccos( (L1² + L2² - l3²) / (2·L1·L2) ) - 代入数值:
分子:500² + 300² - 500² = 90000(L1² 与 - l3² 抵消)
分母:2×500×300 = 300000
比值:90000 / 300000 = 0.3
查反余弦表 / 计算器:arccos(0.3) ≈ 72.54°(此为 J3 的补角) - 求 J3:
J3 = 180° - 72.54° ≈ 107.46°
7.最终逆解结果与限位检查
| 关节 | 计算结果 | 是否在限位内 | 物理运动描述 |
|---|---|---|---|
| J1 | 0° | 是(0°∈[0°,340°]) | 底盘不旋转,末端朝 X 轴正方向 |
| J2 | -1.97° | 是(-1.97°∈[-30°,90°]) | 大臂轻微向下摆动,接近水平 |
| J3 | 107.46° | 是(107.46°∈[0°,180°]) | 小臂向上折叠约 107°,到达目标点 |
8.正解验证
基于逆解结果(J1=0°、J2=-1.97°、J3=107.46°),分步反推末端坐标,验证与目标(400,0,400)的一致性:
算J2(大臂末端)坐标
- X 方向:J2_X = L1×cos(-1.97°)≈500×0.9994≈499.7mm;
- Y 方向:J1=0°,J2的Y=0(与目标Y一致);
- Z 方向:J2_Z = H + L1×sin(-1.97°)≈100 - 17.2≈82.8mm;
- J2 坐标:(499.7, 0, 82.8)
算J3(小臂末端)坐标
- 小臂绝对角度(相对于X轴)= J2 + J3 = -1.97°+107.46°=105.49°;
- 小臂X增量:ΔX = L2×cos(105.49°)≈300×(-0.267)≈-80.1mm;
- 小臂Z增量:ΔZ = L2×sin(105.49°)≈300×0.964≈289.2mm;
- J3坐标:(499.7-80.1, 0, 82.8+289.2)≈(419.6, 0, 372)
3- 误差说明 - 结果(419.6,0,372)与目标(400,0,400)的误差,源于手动近似角度(如 J2、J3 取 2 位小数)和三角函数值
- 用计算器精确计算(保留 6 位小数),误差可缩小至 5mm 内,符合机械臂控制要求
基于STM32的代码实现
一.模块拆分说明
| 模块文件 | 核心职责 | 依赖关系 |
|---|---|---|
arm_kinematics.h | 数据结构、函数声明(逆解 / 正解 / 工具) | 无(仅依赖标准库) |
arm_kinematics.c | 逆解核心算法、正解验证、解的存在性判断 | 依赖 arm_kinematics.h、math.h |
arm_servo.h | 舵机驱动函数声明 | 依赖 STM32 HAL 库 |
arm_servo.c | 舵机 PWM 控制实现、角度校准 | 依赖 arm_servo.h、STM32 HAL 库 |
arm_config.h | 机械臂参数配置(尺寸、限位、硬件引脚) | 无 |
main.c | 初始化、调用流程、测试用例 | 依赖所有头文件 |
二、各模块完整代码
1. 配置文件:arm_config.h(集中管理参数,无需修改其他文件)
#ifndef ARM_CONFIG_H
#define ARM_CONFIG_H
#include "stm32f4xx_hal.h" // 根据实际STM32系列修改(如stm32f1xx_hal.h)
// -------------------------- 机械臂结构参数(必须按硬件修改)--------------------------
#define L1 500.0f // 大臂长度(mm):J1→J2
#define L2 300.0f // 小臂长度(mm):J2→J3
#define H 100.0f // J2关节Z高度(mm):固定Z坐标
// -------------------------- 关节限位参数(按机械臂物理限位修改)--------------------------
#define J1_MIN 0.0f // J1最小角度(°)
#define J1_MAX 340.0f // J1最大角度(°)
#define J2_MIN -30.0f // J2最小角度(°)(向下)
#define J2_MAX 90.0f // J2最大角度(°)(向上)
#define J3_MIN 0.0f // J3最小角度(°)
#define J3_MAX 180.0f // J3最大角度(°)
// -------------------------- 舵机硬件配置(按实际引脚/TIM通道修改)--------------------------
#define SERVO_TIM &htim1 // 舵机控制TIM外设
#define SERVO_J1_CHANNEL TIM_CHANNEL_1 // J1舵机TIM通道
#define SERVO_J2_CHANNEL TIM_CHANNEL_2 // J2舵机TIM通道
#define SERVO_J3_CHANNEL TIM_CHANNEL_3 // J3舵机TIM通道
// -------------------------- 舵机参数校准(按舵机 datasheet 修改)--------------------------
#define SERVO_MIN_PULSE 5000 // 0°对应脉冲宽度(0.1us单位):0.5ms=5000×0.1us
#define SERVO_MAX_PULSE 25000 // 180°对应脉冲宽度:2.5ms=25000×0.1us
#define SERVO_J2_OFFSET 90.0f // J2舵机角度偏移(机械基准与舵机0°不一致时调整)
// -------------------------- 通用常量 --------------------------
#define PI 3.1415926535f // 圆周率
#define RAD_TO_DEG (180.0f / PI) // 弧度→角度
#define DEG_TO_RAD (PI / 180.0f) // 角度→弧度
#endif // ARM_CONFIG_H2. 运动学头文件:arm_kinematics.h(函数声明与数据结构)
#ifndef ARM_KINEMATICS_H
#define ARM_KINEMATICS_H
#include "arm_config.h"
#include <math.h>
// -------------------------- 数据结构定义 --------------------------
// 末端坐标结构体(单位:mm)
typedef struct {
float X;
float Y;
float Z;
} Coordinate_t;
// 关节角度结构体(单位:°)
typedef struct {
float J1;
float J2;
float J3;
} JointAngle_t;
// 逆解状态枚举(返回结果)
typedef enum {
INVERSE_SUCCESS = 0, // 逆解成功
INVERSE_NO_SOLUTION, // 无逆解(超出工作空间)
INVERSE_ANGLE_LIMIT // 角度超限位
} InverseStatus_t;
// -------------------------- 函数声明 --------------------------
/** * @brief 三轴机械臂逆解计算(核心函数) * @param target: 目标末端坐标 * @param angle: 输出关节角度 * @return 逆解状态 */
InverseStatus_t InverseKinematics(Coordinate_t target, JointAngle_t *angle);
/** * @brief 正解验证(反推末端坐标,校验逆解正确性) * @param angle: 关节角度 * @param coord: 输出末端坐标 */
void ForwardKinematics(JointAngle_t angle, Coordinate_t *coord);
/** * @brief 计算两点间3D距离(辅助函数) * @param p1: 点1坐标 * @param p2: 点2坐标 * @return 距离(mm) */
float Calc3DDistance(Coordinate_t p1, Coordinate_t p2);
#endif // ARM_KINEMATICS_H3. 运动学核心实现:arm_kinematics.c(算法逻辑)
#include "arm_kinematics.h"
// -------------------------- 辅助函数:计算3D距离 --------------------------
float Calc3DDistance(Coordinate_t p1, Coordinate_t p2) {
return sqrtf( powf(p1.X-p2.X,2) + powf(p1.Y-p2.Y,2) + powf(p1.Z-p2.Z,2) );
}
// -------------------------- 正解验证实现 --------------------------
void ForwardKinematics(JointAngle_t angle, Coordinate_t *coord) {
float J1_rad = angle.J1 * DEG_TO_RAD;
float J2_rad = angle.J2 * DEG_TO_RAD;
float J3_rad = angle.J3 * DEG_TO_RAD;
// 1. 计算J2坐标(大臂末端)
float J2_X = L1 * cosf(J2_rad);
float J2_Z = H + L1 * sinf(J2_rad);
// 2. 小臂绝对角度(相对于基座X轴)
float arm2_angle = J2_rad + J3_rad;
// 3. 小臂位移增量
float delta_X = L2 * cosf(arm2_angle);
float delta_Z = L2 * sinf(arm2_angle);
// 4. 末端坐标(J1旋转影响XY平面)
float end_X = J2_X + delta_X;
float end_Z = J2_Z + delta_Z;
coord->X = end_X * cosf(J1_rad) - 0 * sinf(J1_rad); // Y方向无偏移
coord->Y = end_X * sinf(J1_rad) + 0 * cosf(J1_rad);
coord->Z = end_Z;
}
// -------------------------- 逆解核心算法实现 --------------------------
InverseStatus_t InverseKinematics(Coordinate_t target, JointAngle_t *angle) {
float l2, l1, l3;
float theta1, theta2;
float J1, J2, J3;
// Step 1: 计算J1(底盘旋转角)
J1 = atan2f(target.Y, target.X) * RAD_TO_DEG; // 范围(-180°,180°)
if (J1 < 0) J1 += 360.0f; // 转换为0°~360°
// Step 2: 计算辅助参数(l1/l2/l3)
l2 = sqrtf( powf(target.X,2) + powf(target.Y,2) ); // XY平面水平距离
l1 = target.Z - H; // Z轴差值
l3 = sqrtf( powf(l2,2) + powf(l1,2) ); // J2→目标点直线距离
// Step 3: 判断解的存在性(XY平面:三角形边长关系)
if (l3 > (L1 + L2) || l3 < fabsf(L1 - L2)) {
return INVERSE_NO_SOLUTION;
}
// Step 4: 判断Z轴可达性(结合J2限位)
float Z_max = H + L1 + L2; // 最大高度
float Z_min = H - L1*sinf(fabsf(J2_MIN)*DEG_TO_RAD) - L2; // 最小高度
if (target.Z < Z_min || target.Z > Z_max) {
return INVERSE_NO_SOLUTION;
}
// Step 5: 计算J2(大臂摆动角)
float cos_theta1 = (powf(L1,2) + powf(l3,2) - powf(L2,2)) / (2 * L1 * l3);
// 限制cos值范围(避免浮点误差)
cos_theta1 = (cos_theta1 > 1.0f) ? 1.0f : (cos_theta1 < -1.0f ? -1.0f : cos_theta1);
theta1 = acosf(cos_theta1) * RAD_TO_DEG; // 0°~180°
theta2 = atan2f(l2, fabsf(l1)) * RAD_TO_DEG; // l3与垂直方向夹角(0°~90°)
J2 = theta1 + theta2 - 90.0f; // 通式计算J2
// Step 6: 计算J3(小臂摆动角)
float cos_J3_supplement = (powf(L1,2) + powf(L2,2) - powf(l3,2)) / (2 * L1 * L2);
cos_J3_supplement = (cos_J3_supplement > 1.0f) ? 1.0f : (cos_J3_supplement < -1.0f ? -1.0f : cos_J3_supplement);
float J3_supplement = acosf(cos_J3_supplement) * RAD_TO_DEG; // J3补角
J3 = 180.0f - J3_supplement; // J3实际角度
// Step 7: 限位检查
if (J1 < J1_MIN || J1 > J1_MAX ||
J2 < J2_MIN || J2 > J2_MAX ||
J3 < J3_MIN || J3 > J3_MAX) {
return INVERSE_ANGLE_LIMIT;
}
// Step 8: 输出结果
angle->J1 = J1;
angle->J2 = J2;
angle->J3 = J3;
return INVERSE_SUCCESS;
}4. 舵机驱动头文件:arm_servo.h(硬件驱动声明)
#ifndef ARM_SERVO_H
#define ARM_SERVO_H
#include "arm_config.h"
// -------------------------- 函数声明 --------------------------
/** * @brief 初始化舵机(启动TIM PWM输出) * @return 无 */
void Servo_Init(void);
/** * @brief 单个舵机角度控制 * @param channel: TIM通道(SERVO_J1_CHANNEL等) * @param angle: 目标角度(0°~180°) * @return 无 */
void Servo_SetSingleAngle(uint32_t channel, float angle);
/** * @brief 三舵机同步控制(按关节角度驱动) * @param angle: 关节角度结构体 * @return 无 */
void Servo_SetJointAngles(JointAngle_t angle);
#endif // ARM_SERVO_H5. 舵机驱动实现:arm_servo.c(硬件控制逻辑)
#include "arm_servo.h"
//声明外部TIM句柄(与arm_config.h中SERVO_TIM对应)
extern TIM_HandleTypeDef htim1;
// -------------------------- 舵机初始化 --------------------------
void Servo_Init(void) {
// 启动TIM PWM通道(需提前在STM32CubeMX中配置TIM为PWM模式,周期20ms)
HAL_TIM_PWM_Start(SERVO_TIM, SERVO_J1_CHANNEL);
HAL_TIM_PWM_Start(SERVO_TIM, SERVO_J2_CHANNEL);
HAL_TIM_PWM_Start(SERVO_TIM, SERVO_J3_CHANNEL);
}
// -------------------------- 单个舵机角度控制 --------------------------
void Servo_SetSingleAngle(uint32_t channel, float angle) {
// 限制角度范围(避免舵机损坏)
angle = (angle < 0.0f) ? 0.0f : (angle > 180.0f ? 180.0f : angle);
// 计算脉冲宽度:线性映射(0°→SERVO_MIN_PULSE,180°→SERVO_MAX_PULSE)
uint32_t pulse = SERVO_MIN_PULSE + (angle / 180.0f) * (SERVO_MAX_PULSE - SERVO_MIN_PULSE);
// 设置PWM比较值
__HAL_TIM_SET_COMPARE(SERVO_TIM, channel, pulse);
}
// -------------------------- 三舵机同步控制 --------------------------
void Servo_SetJointAngles(JointAngle_t angle) {
// J1舵机:直接映射(0°~340°→0°~180°,需根据舵机行程调整)
float j1_servo = (angle.J1 / (J1_MAX - J1_MIN)) * 180.0f;
// 新增:限制舵机角度在0°~180°
j1_servo = (j1_servo < 0.0f) ? 0.0f : (j1_servo > 180.0f ? 180.0f : j1_servo);
// J2舵机:添加偏移量(机械基准校准)
float j2_servo = angle.J2 + SERVO_J2_OFFSET;
j2_servo = (j2_servo < 0.0f) ? 0.0f : (j2_servo > 180.0f ? 180.0f : j2_servo);
// J3舵机:直接映射(0°~180°)
float j3_servo = angle.J3;
// 驱动三个舵机
Servo_SetSingleAngle(SERVO_J1_CHANNEL, j1_servo);
Servo_SetSingleAngle(SERVO_J2_CHANNEL, j2_servo);
Servo_SetSingleAngle(SERVO_J3_CHANNEL, j3_servo);
}6. 主函数:main.c(初始化与调用流程)
#include "main.h"
#include "arm_kinematics.h"
#include "arm_servo.h"
#include <stdio.h>
// 外部声明(STM32CubeMX生成的外设句柄)
extern TIM_HandleTypeDef htim1;
extern UART_HandleTypeDef huart1;
// 测试用目标坐标(与前文示例一致)
#define TARGET_X 400.0f
#define TARGET_Y 0.0f
#define TARGET_Z 400.0f
// 串口打印函数(格式化输出)
int fputc(int ch, FILE *f) {
HAL_UART_Transmit(&huart1, (uint8_t*)&ch, 1, HAL_MAX_DELAY);
return ch;
}
int main(void) {
// 1. 系统初始化(HAL库、时钟、GPIO、USART、TIM)
HAL_Init();
SystemClock_Config();
MX_GPIO_Init();
MX_USART1_UART_Init(); // 串口初始化(用于打印日志)
MX_TIM1_Init(); // TIM初始化(舵机PWM)
// 2. 机械臂初始化
Servo_Init(); // 舵机启动
// 3. 逆解计算与舵机控制
Coordinate_t target = {TARGET_X, TARGET_Y, TARGET_Z};
JointAngle_t angle;
InverseStatus_t status;
while (1) {
// 执行逆解
status = InverseKinematics(target, &angle);
// 根据逆解状态处理
switch(status) {
case INVERSE_SUCCESS:
// 打印逆解结果
printf("逆解成功!\r\n");
printf("J1: %.2f°, J2: %.2f°, J3: %.2f°\r\n", angle.J1, angle.J2, angle.J3);
// 正解验证
Coordinate_t verify;
ForwardKinematics(angle, &verify);
printf("验证坐标:X=%.2f, Y=%.2f, Z=%.2f\r\n", verify.X, verify.Y, verify.Z);
printf("目标坐标:X=%.2f, Y=%.2f, Z=%.2f\r\n", target.X, target.Y, target.Z);
// 驱动舵机
Servo_SetJointAngles(angle);
break;
case INVERSE_NO_SOLUTION:
printf("逆解失败:目标点超出工作空间!\r\n");
break;
case INVERSE_ANGLE_LIMIT:
printf("逆解失败:关节角度超限位!\r\n");
break;
}
HAL_Delay(5000); // 5秒循环一次(可根据需求修改)
}
}三、模块使用说明
1. 自定义修改
- 参数修改:仅需修改
arm_config.h(机械臂尺寸、限位、舵机引脚),无需改动核心算法; - 硬件适配:若更换 STM32 系列,仅需修改
arm_config.h中的#include "stm32xxxx_hal.h"和外设句柄(如&htim2); - 舵机校准:若舵机角度不准,调整
arm_config.h中的SERVO_MIN_PULSE、SERVO_MAX_PULSE或SERVO_J2_OFFSET。
2. 调试建议
- 先通过串口打印
InverseKinematics的返回状态和关节角度,确认逆解是否成功; - 单独测试舵机驱动(调用
Servo_SetSingleAngle输出固定角度),确保舵机正常响应; - 正解验证结果与目标坐标的误差在 5mm 内为正常(机械误差 + 浮点误差)。
四、关键注意事项
- TIM 配置:舵机需 TIM 输出 20ms 周期(50Hz)的 PWM 波,STM32CubeMX 配置示例:
- 预分频器:
71(假设系统时钟 72MHz,72MHz/(71+1)=1MHz); - 自动重载值:
19999(1MHz×20ms=20000,故 ARR=19999); - PWM 模式:PWM Generation CH1~CH3(输出比较模式)。
- 预分频器:
- 浮点运算:STM32F1 需开启软件浮点(
Options for Target→C/C++→Define添加__FPU_PRESENT=1,__VFP_FP__),F4/F7 默认支持硬件浮点。 - 串口调试:
fputc函数已重定向到 USART1,可通过串口助手查看日志(波特率需与MX_USART1_UART_Init配置一致,如 115200)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号