图-宽度/深度优先遍历

图的存储方式

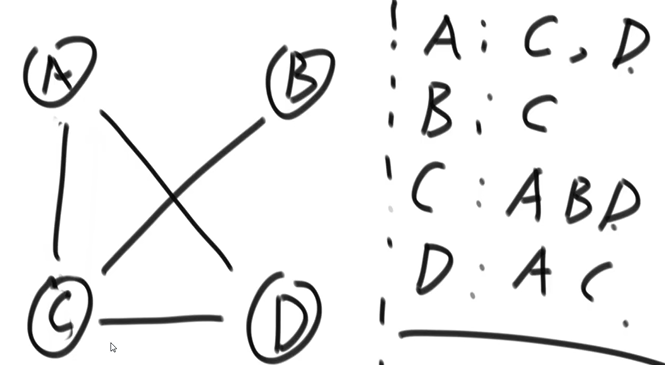
• 邻接表
  

• 邻接矩阵
  正方形矩阵
  A B C D
  A 0 - 7 3
  B - 0 2 -
  C 7 2 0 5
  D 3 - 5 0

表达图。。。 生成图
有向图 无向图 权值
点 + 边

点如下

public class Node {
    // 点集
    public int value; // 编号，值
    public int in; // 入度 ，有多少个进入这个点, 无向图，入度和出度一样。
    public int out; // 出度 ，
    public ArrayList<Node> nexts; // 从当前点出发，发散出去的点，直接邻居。
    public ArrayList<Edge> edges; // 属于我的边 有哪些。 A→B from 是 当前node.

    public Node(int value) {
        this.value = value;
        in = 0;
        out = 0;
        nexts = new ArrayList<>();
        edges = new ArrayList<>();
    }

}

边如下

public class Edge {
    public int weight; // 权重
    public Node from; // 从哪个node 出发
    public Node to; // 到哪个node

    public Edge(int weight, Node from, Node to) {
        this.weight = weight;
        this.from = from;
        this.to = to;
    }
}

图结构如下

public class Graph {
    public HashMap<Integer, Node> nodes;
    public HashSet<Edge> edges;

    public Graph() {
        nodes = new HashMap<>();
        edges = new HashSet<>();
    }

}

生成图， 其他结构类型的图，生成 自己的这个图

public static Graph generatorGraph(Integer[][] matrix) {

    // matrix 二维数组，
    // matrix[0][0] = from,
    // matrix[0][1] = to,
    // matrix[0][2] = weight
    Graph graph = new Graph();

    for (int i = 0; i < matrix.length; i++) {
        Integer from = matrix[i][0];
        Integer to = matrix[i][1];
        Integer weight = matrix[i][2];

        // 判断当前点是否已经加入nodes
        if (!graph.nodes.containsKey(from)) {
            graph.nodes.put(from, new Node(from));
        }
        if (!graph.nodes.containsKey(to)) {
            graph.nodes.put(to, new Node(to));
        }

        Node fromNode = graph.nodes.get(from);
        Node toNode = graph.nodes.get(to);

        Edge edge = new Edge(weight, fromNode, toNode);
        fromNode.out ++;
        toNode.in ++;
        fromNode.nexts.add(toNode);
        graph.edges.add(edge);

    }
    return graph;
}

图的宽度优先遍历

1） 宽度，都是队列
2） 从源节点开始依次按照宽度 进 队列， 然后弹出
3） 每弹出一个点，把该节点所有没有进过队列的 邻接点 放入队列
4） 直到队列为空
和二叉树的区别，可能有环 。要注意，使用一个set保存已经进入过队列的 node

public static void graphBFS(Node node) {
    if (node == null) {
        return;
    }
    LinkedList<Node> queue = new LinkedList<>();
    HashSet<Node> set = new HashSet<>(); // 保存已经进入过 queue的node
    // 节点入队
    queue.add(node);
    set.add(node);

    Node cur = null;
    // 开始循环 出队
    while (!queue.isEmpty()) {
        cur = queue.poll();
        // 打印处理
        System.out.println(cur.value);
        // 把当前节点 的邻接点 都入队
        for (Node tmpNode : cur.nexts) {
            // 判断是否已经进入过队列
            if (set.contains(tmpNode)) {
                continue;
            }
            queue.add(tmpNode);
            set.add(tmpNode);
        }
    }
}

图的深度优先遍历

1）深度，使用栈
2）从源节点开始把节点按照深度放入栈， 然后弹出，
3）每弹出一个点，把该节点 下一个 没有进过栈的邻接点 放入栈 , 只放一个。还要把当前节点也压进去。处理next节点。
如果都已经进过栈了。开始弹上一个
栈永远保存当前深度路劲

4）直到栈为空

public static void graphDFS(Node node){
    if(node == null){
        return;
    }

    HashSet<Node> set = new HashSet<>();
    Stack<Node> stack = new Stack<>();

    stack.push(node);
    set.add(node);

    //先处理 第一个节点
    System.out.println(node.value);

    while(!stack.isEmpty()){
        // 开始出栈
        Node cur  = stack.pop();

        // 遍历 当前节点的 nexts 
        for (Node nextNode : cur.nexts) {              
            if(!set.contains(nextNode)){
                //如果当前下一个节点 没 入过栈 ，开始处理当前节点，
                
                // 又因为栈要一直保存当前 深度，所以要把当前节点再压进去
                stack.push(cur);
                stack.push(nextNode);

                // 当前nextNode 加入到 set
                set.add(nextNode);

                //打印处理 nextNode 
                System.out.println(nextNode);
                // 只走一条路，所以直接break
                break; 
                
            }            
        }
        // 如果当前节点的下一个节点都 进入过栈，就开始依次弹出上面的节点。
    }
            
}